Исследование механических свойств технического пластилина при квазистатическом и динамическом деформировании

Технический пластилин (ТП) находит широкое применение, например, при тестировании средств индивидуального бронирования как среда, регистрирующая форму и глубину вмятины после удара пулей или ножом в бронежилет [1, 2], как модельный материал при изучении процессов обработки давлением (ковка, штамповка, прокатка [3–8]), при моделировании процессов пенетрации [9–16]. При нормальных условиях пластилин показывает себя низкомодульным вязкоупругим материалом. Его механические свойства существенно зависят от температуры и скорости деформирования. ТП представляет собой многокомпонентный композитный материал – высоковязкую суспензию воска, жиров и ультрамелкодисперсных наполнителей (талька, глин и пигментов). Трудность работы с ним заключается в его сравнительно низких механических свойствах, требующих высокоточного оборудования и тщательного контроля температуры испытаний. ТП не являет- ся конструкционным материалом, и этим определяется отсутствие справочных данных о его механических свойствах. Отметим также, что математические модели пластилина используются в численных методах оценки качества бронежилетов [9–15], поэтому исследования механических свойств ТП являются актуальными.

В данной работе исследования проведены на скульптурном пластилине c долей наполнителя около 50 % в широком диапазоне скоростей деформирования (шесть порядков) при нормальных условиях (температура окружающей среды +20°±1°С). Показано, что ТП проявляет степенную зависимость предела текучести от скорости деформирования, т.е. представляет собой существенно реономную среду с возможностью накопления рассеянных микроповреждений и разрушением при больших деформациях.

1.    Методика исследования и результаты

Проведены квазистатические испытания ТП на растяжение, сжатие и сдвиг. Замер деформаций проводили с использованием бесконтактного видеоэкстензометра AVE, входящего в комплект универсальной испытательной машины INSTRON 5882: на образец крепили метки, которые идентифицирует AVE, находит геометрический центр каждой метки и вычисляет текущее расстояние между ними. Метки должны следовать за деформациями образца, т.е. прочно крепиться к поверхности пластилина. В качестве меток использовали бумагу.

Рис. 1. Образцы для испытаний на растяжение – 1 , сжатие – 2 и сдвиг – 3

Метки должны контрастировать с поверхностью образца, поэтому в AVE используется плоско поляризованный источник света, а материал меток должен обеспечивать деполяризацию света. Это легко выполняется на металлических поверхностях и не всегда на резине или пластике. При невозможности использования меток (большие деформации сжатия) использовали для замера деформаций датчик перемещения траверсы машины. Погрешность измерения удлинения образца соответствовала погрешности измерения перемещения траверсы машины (±1 мкм), так как жесткость образцов была на несколько порядков ниже жесткости машины и силоизмерителя. Общий вид образцов для испытаний показан на рис. 1.

Испытания на растяжение

Из пластины ТП толщиной 5 мм на вырубном прессе IDM получены стандартные для низкомодульных материалов образцы (ASTM D412 тип 4), которые закрепляли в тисочных захватах Instron 2710-106 (рис. 2). Образцы имели общую длину 100 мм, длину и ширину рабочей части 20 и 5 мм соответственно и захватные части шириной 15 мм.

Рис. 2. Образец с метками для испытаний на растяжение в тисочных захватах

Силоизмеритель c пределом 100 Н был использован для фиксации нагрузки, скорость движения захвата варьировали в диапазоне 1–400 мм/мин. Полученные кривые «нагрузка – перемещение» обработали в кривые «условное напряжение – деформация». Диаграммы растяжения в условных напряжениях приведены на рис. 3. Цифры у кривых – скорость деформирования, с–1, которая вычисляется как отношение скорости перемещения к начальной длине образца (на рис. 6, 8 и 9 аналогично). Эксперименты показывают наличие спадающих ветвей диаграмм растяжения при деформациях более 3–5 %, чего не было бы, если бы материал работал упругопластически и не имел внутренних микроповреждений (микротрещин и т.п.). Кривые в истинных напряжениях и деформациях не приводятся, так как нет оснований для использования предположения о несжимаемости при растяжении (см. рис. 3).

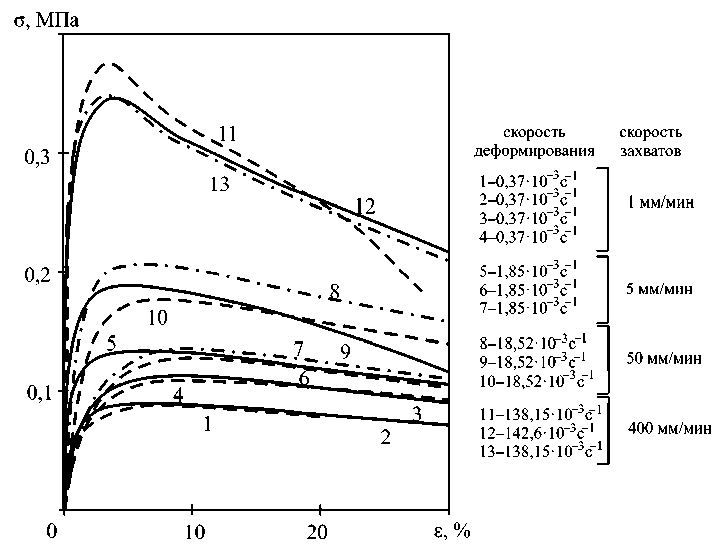
Рис. 3. Диаграммы растяжения

Можно отметить, что образование шейки и начало падающего участка кривой деформирования происходит при разных деформациях (от 4 % при высокой скорости до 10 % при малой скорости деформирования). Обработка начальных участков деформирования показала, что величина модуля упругости равна 30±5 МПа.

Из пластины ТП толщиной 5 мм были вырезаны плоские образцы с размерами 27×5×100 мм, которые закрепляли в тисочных захватах Instron 2710-106 (рис. 4). Скорость движения захвата 5 мм/мин, продольную и поперечную деформации фиксировали с помощью системы DIC (Digital image correlation, фирма Correlated Solution), скорость съемки составляла 1 кадр/с, схема 2D (съемка одной камерой). На по- верхность образца были установлены специальные маркеры для фиксации продольной и поперечной деформации. Маркеры представляли собой канцелярские «гвоздики» с плоской шляпкой, у которых игольчатая часть была полностью погружена в образец. Иные способы крепления маркеров не позволили получить надежные результаты. Полученные зависимости «отношение поперечной деформации к продольной – продольная деформация» приведены на рис. 5, штрих-пунктир – полиномиальная аппроксимация, сглаживающая экспериментальные данные. При малых деформациях коэффициент Пуассона равен 0,30 и далее увеличивается до 0,45 при продольной деформации 3 %. Дальнейшее увеличение деформаций приводит к появлению микроповреждений (отслоение матрицы от твердых включений) и возникновению микрополостей, деформации которых приводят к немонотонному изменению отношения поперечной деформации к продольной. На рис. 5 приведена также расчетная зависимость отношения поперечной деформации к продольной для несжимаемого материала с начальным коэффициентом Пуассона 0,5. Различия достаточно очевидны, чтобы говорить о нарушении гипотезы несжимаемости при растяжении при деформациях, больших 3–5 %.

Рис. 4. Образец с метками для определения коэффициента Пуассона при растяжении

Si/Ej

0,4

0,3

0,2

0,1-

о Экспериментальные точки

— Аппроксимация

X^)=44750jc -18102?+3118,6?-266,39?+8,838^+0,342

— г^у для несжимаемого материала

0         2       4       6       8       10      12      £г%

Рис. 5. Зависимость «поперечная деформация – продольная деформация» при растяжении

Испытания на сжатие

Из пластины ТП толщиной около 30 мм были вырезаны образцы в виде параллелепипеда со средними размерами 15×15×30 мм, которые испытали на сжатие между плоскими плитами со скоростями 1, 5, 50 и 500 мм/мин. Диаграммы сжатия в условных напряжениях приведены на рис. 6.

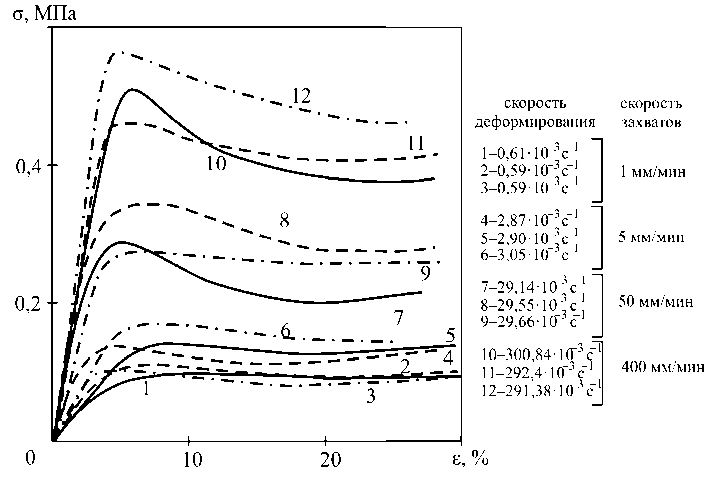
Рис. 6. Диаграммы сжатия ТП

Разброс механических свойств материала связан, очевидно, с неоднородностью структуры и зависимостью свойств от температуры (контроль температуры образца с погрешностью, меньшей 1 °С, был невозможен).

Испытания на сдвиг

Из пластины ТП толщиной 3,5 мм были вырезаны образцы в виде параллелепипеда с размерами 3,5×26×40 мм, которые закрепили между стеклянными пластинами толщиной 2 мм и испытали на чистый сдвиг (рис. 7) со скоростями сближения захватов 0,1–81 мм/мин. Высокая адгезия пластилина к стеклу после небольшого поджатия позволяет проводить испытания вплоть до разрушения без дополнительного клея. Диаграммы сдвига приведены на рис. 8.

Рис. 7. Образец для испытаний на сдвиг в тисочных захватах

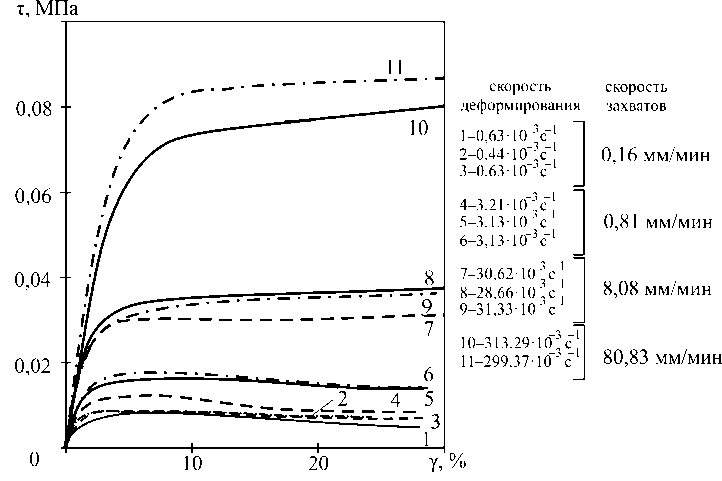
Рис. 8. Диаграммы сдвига ТП

Динамическое сжатие

Образцы с размерами 15×15 мм (площадь поперечного сечения S = 225 мм²) и длиной L 0 = 30 мм нагружали падающим грузом массой m = 200 г с высоты H = 0,1–1 м. Сопротивление воздуха не учитывали. Регистрировали остаточную длину A L образцов после испытаний для вычисления предела текучести о т и скорости деформирования £ в предположении идеальной текучести и пренебрежении тепловыми эффектами (потенциальная энергия груза полностью переходит в работу пластического деформирования):

о т = mgH I SS -A L ) , £= 2gHH /( 2 L „) .              (1)

Значения пределов текучести в функции от скорости деформирования приведены на рис. 11.

Статическое индентирование

Альтернативой сжатию призматических образцов могут служить испытания на индентирование. В данной работе в поверхность ТП с размерами 180×180×75 мм вдавливали стальную сферу диаметром D = 43 мм и массой m = 321 г. Она была закреплена на верхнем захвате и до испытания не касалась поверхности образца. Сферу внедряли со скоростями 5, 20 и 100 мм/мин на испытательной машине INSTRON 5882. Диаграммы индентирования «усилие Р – глубина внедрения u » представлены на рис. 9. Можно заметить, что в начале диаграммы ин-дентирования наблюдается нелинейность, но эта область достаточно мала, чтобы аппроксимировать линейной функцией диаграмму индентиро-вания до глубины 2–3 мм без потери точности. Это позволяет считать твердость ТП по Бринеллю неизменной величиной в этом диапазоне.

После разгрузки на поверхности ТП регистрировали диаметр d отпечатка методом фотографирования с обработкой изображения на компьютере. Погрешность измерения диаметра не превышала 0,1 мм. Глубину отпечатка вычисляли по формуле h = — - - 7 D2 - d2

В источниках [17–19] для весьма пластичных металлов приводится линейная связь твердости по Бринеллю с пределом прочно-сти/текучести от = к • HB, HB = P/ (2пRh), (3) здесь P - сила; R - радиус сферы; 2пRh - площадь поверхности отпечатка; к - коэффициент, равный 0,33-0,36 для сталей.

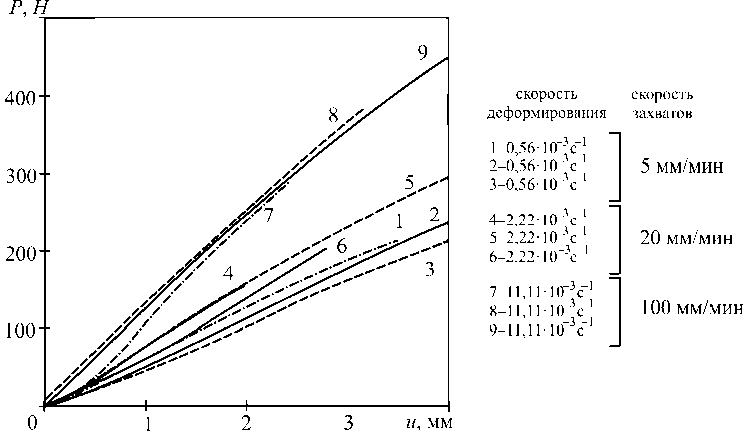
Рис. 9. Кривые индентирования при статическом нагружении

Для расчета скорости деформирования необходимо иметь информацию о размере очага деформации под индентором, где материал испытывает сжатие, по аналогии с длиной образца L ₀ , на которую производится деление скорости движения траверсы и при испытаниях на сжатие призматических образцов. Очагом деформации в данной работе считается объем, испытывающий напряжения сжатия, составляющие не менее 5 % от максимального значения под индентором. Размеры очага деформации можно приближенно оценить, используя решение задачи Буссинеска (действие сосредоточенной силы на упругое полупространство) [20, 21]. В соответствии с этим решением радиальные напряжения сжатия изменяются по глубине образца по зависимости

3 P 1

^{О (} r ) = - F.                             ⁽⁴⁾

2п r где r - расстояние от точки приложения нагрузки. Учитывая, что напряжение на площадке контакта равно HB (см. зависимость (3)), то глубину очага деформации несложно найти из условия о(r=L0)=HB/20. Отсюда следует, что

L ₀ = V 60 R ■ h . (5)

Для оценки корректности (5) проведен статический расчет напряженного состояния в зоне контакта пластилина со сферическим индентором в конечно-элементном пакете ANSYS Workbench v.14.5. В осесимметричной 2D модели материал пластилина и сферы задавали идеально упругими. Сфера была выполнена из стали, а упругие характеристики пластилина приняты следующими: Е = 25 МПа, р = 0,3. Сферический индентор в расчете перемещали на 3 мм с автоматическим определением реакций опор (964 Н). Среднее напряжение сжатия на площадке контакта составляли 4,08 МПа (радиус площадки контакта и ее глубина составляли 8,5 и 1,75 мм соответственно). Значение, соответствующее 5 % от 4,08 МПа, равно 0,20 МПа. В результате расчета «длина образца L 0 » составила L 0 = 47,5 мм (рис. 10). Подстановка найденных значений в (5) дает L ₀ = ^ 60 ■ 21,5 ■ 1,75 = 47,5 мм. Совпадение вполне удовлетворительное.

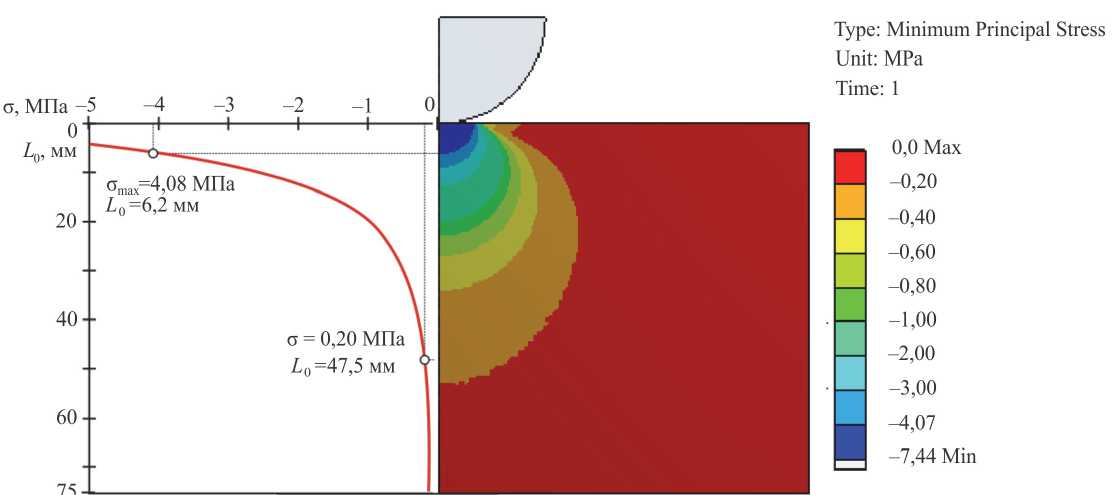
Рис. 10. Распределение сжимающих напряжений при индентировании

Если пластилин проявляет пластические свойства, то связь предела текучести и величиной твердости по Бринеллю (3) определяется коэффициентом k = 0,24 при отсутствии трения. Это было показано статическим расчетом в конечно-элементном пакете ANSYS Workbench v.14.5. В осесимметричной 2D-модели материал пластилина задавали упруго-идеально-пластическим (билинейная диаграмма деформирования с нулевым упрочнением), а материал сферы (диаметр 43 мм) – сталь (идеально упругий). Отличие найденного коэффициента от величины 0,33–0,36 (3) объясняется практической недеформируемостью стального индентора в контакте с пластилином в отличие от испытания сталей. Диаграмма индентирования была практически линейной вплоть до максимального перемещения 3 мм.

Отмеченная линейность диаграмм индентирования оказывается полезной для анализа и сравнения статической и динамической твердости. В работах [22–25] введено понятие «динамической твердости» как частного от деления энергии падающего тела на объем вытесненного материала. В условиях квазистатического нагружения это соответствует энергии деформирования Э (площадь под кривой инденти-рования), деленной на объём отпечатка V в ТП. Результаты расчетов (таблица) показывают, что статическая и динамическая твердости близки, если скорости деформирования совпадают. Динамическую твердость вычисляли по зависимости

Э d P ' u 17    1 HB = —, Э =--- , V =n h V 2 Сопоставление значений статической и			Г d 2 h 22) —+— .           (6) L 8 6 J динамической твердости
	Скорость деформирования 10–3, 1/с	Статическая твердость, МПа	Динамическая твердость, МПа	Погрешность, %
1	0,89	0,45	0,48	6,25
2	0,89	0,44	0,47	6,38
3	0,89	0,39	0,43	9,30
среднее	0,89	0,43	0,46	7,31
4	3,50	0,58	0,60	3,33
5	3,50	0,53	0,56	5,36
6	3,50	0,55	0,59	6,78
среднее	3,50	0,55	0,58	5,16
7	17,53	0,89	0,92	3,26
8	17,53	0,90	0,95	5,26
9	17,53	0,83	0,89	6,74
среднее	17,53	0,87	0,92	5,07

Динамическая твердость (ударное индентирование)

На поверхность ТП с размерами 180×180×75 мм с высоты H = 0,1–1 м вертикально сбрасывали сферический индентор диаметром D = 43 мм и массой m = 321 г. Сопротивлением воздуха пренебрегали.

Измеряли диаметр отпечатка методом фотографирования, аналогично п. «Статическое индентирование» и вычисляли его глубину по формуле (2).

Динамическую твердость вычисляли по зависимости (6), в которой вместо 0,5 Pu использовали потенциальную энергию падающего тела mgH . Вычисление динамических пределов текучести проводили по зависимости (3). На рис. 11 представлена степенная зависимость предела текучести от скорости деформирования и экспериментальные точки при квазистатическом и динамическом нагружениях, которая в двойных логарифмических координатах имеет вид линейной функции.

о, МПа

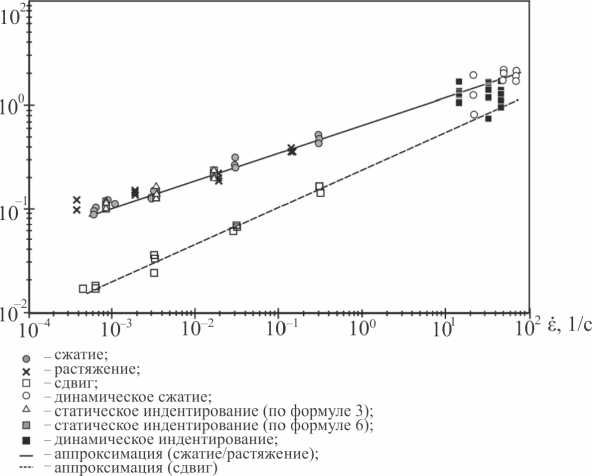
Рис. 11. Зависимости пределов текучести от скорости деформирования

Аппроксимирующая кривая для случая растяжения/сжатия/ин-дентирования имеет вид степенного закона:

о _т = 6,37 - 10 5 -ё ^0,266.                             (7)

Для чистого сдвига это уравнение несколько иное:

о _т = 2,23 - 10 5 -ё ^0,3 4 ⁷.                               (8)

Однако при высоких скоростях деформирования результаты сближаются, что делает возможным использование классических теорий пластичности при анализе баллистических задач со скоростями деформирования более 104 с–1. Иными словами, технический пластилин в расчетах на растяжение/сжатие может быть имитирован моделью типа Нортона (вязкоупругое тело с последовательно соединенным упругим и вязким элементами). У вязкого элемента скорость ползучести зависит от приложенного напряжения в соответствии со степенным законом типа Ё = 1,54 • 10-22 о3,759 .

2.    Результаты испытаний и их анализ

Получено, что технический пластилин при растяжении и сжатии имеет близкие значения физических пределов текучести в диапазоне скоростей деформирования 0,0004–80 с–1. Однако испытания на сдвиг нарушают наблюдаемую картину: предел текучести при сдвиге оказывается связан с пределами текучести на растяжение (сжатие) коэффициентом 0,24, тогда как для классического упругопластического материала должно быть 0,5–0,6 (в зависимости от выбранной теории пластичности). Это связано с тем, что при сдвиге не выполняется гипотеза несжимаемости материалов (неизменность объема) при некоторых деформациях из-за развития рассеянных микроповреждений от растягивающей компоненты напряженного состояния (рис. 3 при деформациях больше 3–5 %), т.е. задолго до полного разрушения.

Предел текучести материала при испытаниях на ударное инден-тирование удовлетворительно согласуется с результатами измерений предела текучести при испытаниях на динамическое сжатие призматических образцов.

Выводы

Технический пластилин является полимерным композитом, армированным мелкодисперными наполнителями с объемной долей около 50 %. Он демонстрирует реономное поведение, изменяя предел текучести в 20 раз при изменении скорости деформирования на пять порядков. Материал проявляет при сдвиге и сжатии развитую пластичность, деформации текучести превышают 25–30 %. Однако при растяжении пластилин ведет себя как материал с весьма ограниченной пластичностью, в диапазоне деформаций 3–5 % в нем зарождаются микроповреждения, приводящие к появлению спадающего участка кривой «напряжение – деформация», образованию шейки и разрыву при средних деформациях 25–40 %. При динамическом сжатии падающим грузом предел текучести пластилина достигает величины 2 МПа.

Полученные данные могут быть использованы при численных расчетах кинетики деформирования тканевых бронеструктур, лежащих на вязкоупругом основании, а также при экспериментальном моделировании процессов пластической обработки металлов.