Исследование механического поведения упруготрансформируемых композитных конструкций

ВЕСТНИК ПНИПУ. МЕХАНИКА № 1, 2019PNRPU MECHANICS BULLETIN

Пространственные крупногабаритные космические конструкции, такие как солнечные паруса и рефлекторные антенны, имеют ограничения по массе и способности к размещению внутри объема обтекателей ракет-носителей. Тем не менее большинство космических конструкций имеют гораздо большие размеры, чем пусковые установки, а концепция развертываемых структур позволяет упаковать ее в компактную конфигурацию для укладки и транспортировки, а затем трансформировать до рабочей конфигурации. Данные конструкции становятся все более распространенными из-за высокой весовой эффективности, компактного транспортного состояния, более низкой стоимости, меньшего количества деталей и простоты изготовления.

Значительная часть таких конструкций представляет стержневые системы (фермы), так как в них наиболее эффективно реализуются механические возможности используемых материалов.

Основными элементами конструкции являются: стержни, узлы их сочленения (шарниры), узлы фиксации в рабочем положении и приводы раскрытия (актуаторы). Весовое совершенство пространственной крупногабаритной конструкции и повышение ее надежности требуют снижения веса каждого из ее элементов и по возможности уменьшения их количества.

Достижение данной цели в настоящее время основано на реализации уникальных свойств композиционных материалов (КМ). Основная идея заключается в создании устройства в виде упругого шарнира (УШ) из композиционного материала, который одновременно совмещает функции шарнира, соединяющего стержни и инициирующего их поворот относительно друг друга, обеспечивая тем самым раскрытие фермы, и фиксирует их в заданном положении. УШ представляет собой цилиндрическую тонкостенную оболочку с вырезом в зоне складывания, характеризующимся следующими конструктивными параметрами: толщина t , длина выреза L , ширина выреза h , диаметр «косточки» D (рис. 1).

Теоретические и практические основы создания интеллектуальных и адаптивных конструкций из композиционных материалов с исполнительными элементами, работа которых основана на различных физических законах, рассмотрены в [1, 2].

Различные конструктивные решения упругих элементов и трансформируемых конструкций представлены в [3–7]. Суть сводится к тому, что в сложенном состоянии в шарнирах сосредоточена энергия упругой деформации, которая обеспечивает взаимное переме- щение элементов конструкции при раскрытии, т.е. трансформировании ее в рабочее состояние.

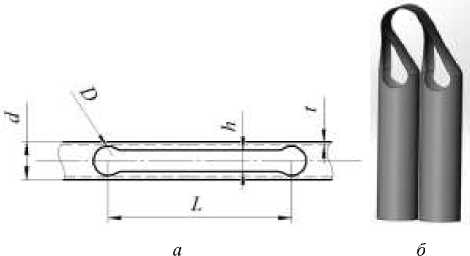
Рис. 1. Композитный УШ: а – начальное состояние и конструктивные параметры; б – сложенное состояние

Fig. 1. Composite tape-spring hinge: а – initial state and geometral properties; b – load application

В работах [8–34] рассматриваются подходы к моделированию квазистатического и динамического поведения композитных ленточных пружин и трубчатых шарниров, а также бистабильных конструкций с эффектом памяти формы. В работах [16, 22–24, 26] для определения упругих и прочностных свойств материала используется микромеханическое моделирование для тканой и плетеной структуры материала, где конечно-элементная (КЭ) модель репрезентативного объема создается в Abaqus. В работах [32, 33] КЭ-модель репрезентативного объема строится в программе TexGenс последующим вычислением матрицы жесткости материала.

В работе [33] описана методика съемки двумя высокоскоростными камерами процесса развертывания композитной трубы с ленточно-пружинным шарниром и измерения углов развертывания. В работе [34] изложена экспериментальная методика получения профиля шарнирного момента путем построения угла складывания, определяемого как разность между углами поворота концевого сечения балки и соответствующими им моментами на каждом шаге.

Следует отметить, что в результате анализа литературных источников не было найдено обоснованной расчетно-экспериментальной методики определения рациональных конструктивных параметров УШ и рекомендаций по его конструированию для достижения заданного шарнирного момента при сохранении прочностных характеристик. Таким образом, разработка комплексной расчетноэкспериментальной методики для определения рациональных параметров УШ является актуальной.

Данная методика включает:

• –    разработку и верификацию модели КМ УШ на основе микромеханического подхода и виртуальных испытаний;

• –    разработку и верификацию КЭ-модели УШ;

• –    серию вычислительных экспериментов по определению влияния конструктивных параметров УШ на шарнирный момент и прочность;

• –    выбор рационального варианта УШ.

Применение данной методики продемонстрирован-но на примере поиска конструктивного решения для разработки УШ с шарнирным моментом 30 Н·м.

В первом разделе статьи описаны технология изготовления УШ и образцов-свидетелей, методика определения упругих и прочностных констант материала УШ посредством натурных механических и виртуальных испытаний.

Во втором разделе описывается методика натурных испытаний УШ.

В третьем разделе описывается методика проведения численного моделирования процесса складывания-раскладывания УШ с характеристиками материала, полученными в первой части.

В четвертом – обсуждаются результаты натурных испытаний и численного моделирования работы УШ.

1.    Определение механических характеристик материалов 1.1.    Изготовление стандартных образцов материалов и упругих шарниров

В исследованиях [16, 22–24, 26] для конструкции упругого шарнира применяются волокна марки Т300 (Torayca). Волокна данной марки обладают высокими значениями прочности (3530 МПа) и модуля упругости (230 ГПа). Ключевой особенностью данного волокна являются высокие продольные деформации до разрушения (1,5 %), что позволяет при изгибе однослойного пакета со схемой армирования [±45] реализовать упругое складывания с деформациями до 5 %.

В работе [35] показано, что для упругого шарнира нежелательно использовать композиты с высоким модулем упругости (высокой жесткостью), как, например, с волокном M46J. Хрупкость и низкая деформация до разрушения высокомодульных волокон, их восприимчивость к образованию трещин делает их непригодными для подобных конструкций. Кроме того, отмечается, что схема армирования [±45] n более устойчива к появлению трещин и разрушению, а однослойный пакет [±45] имеет деформацию до разрушения выше, чем двухслойный [±45] 2 .

В настоящей работе использовалось угольное волокно А-49 (Aksaca) с деформациями до разрушения 2 %. Для создания армирующей преформы использовался метод программируемого армирования, реализованный с помощью радиального плетельного комплекса, в состав которого входят: машина радиального плетения HERZOGRF1/144 100 и многоосевой манипулятор KSLKUKAGWA 180-270 (рис. 2, а ).

Технологический процесс вакуумной инфузии проводился на связующем Т-26 (ИНУМиТ). В процессе вакуумной инфузии, после подготовки, преформа укладывается в технологический пакет и производится вакуумирование (рис. 2, б ). После чего осуществляется инжектирование смолы и нагрев в печи.

а

со схемой укладки волокна [±45]1 и количеством филаментов ровинга 12K. Для упругих и прочностных констант образца направления «1», «2» и X, Y соответственно повернуты на 45° относительно осей ортотропии плетеного монослоя. Направление «3»  – перпендикулярно плоскости монослоя.

Таблица 1

Физико-механические характеристики образцов углепластика при нормальных условиях

Table 1

б

Рис. 2 Процесс производства УШ: а – создание армирующей преформы методом программируемого армирования;

б – формование методом вакуумной инфузии

Fig. 2. Tape-spring hinge production: a – radial braiding of a perform; b – vacuum infusion

Геометрическая модель упругого шарнира представляет собой цилиндрическую оболочку с внешним диаметром d = 46,2 мм с вырезом в зоне складывания. Вырез УШ характеризуется следующими конструктивными параметрами: t = 0,6 мм, L = 204 мм, h = 23 мм, D = 30 мм (см. рис. 1).

Стандартные образцы изготавливались по единой технологии с УШ и являлись образцами-свидетелями. Геометрические характеристики образцов для механических испытаний соответствуют требованиям стандартизованных методов испытания композитов: метод механических испытаний плоских образцов на растяжение (ГОСТ 25.601–80, ASTM D3039M), метод механических испытаний плоских образцов на сжатие (ГОСТ 25.602– 80, ASTM D3410M).

• 1.2.    Результаты испытаний стандартных образцов материалов на растяжение-сжатие

  Статические испытания проводились с использованием универсальной электромеханической машины Instron 5882 (100 кН), специализированной оснастки для растяжения, сжатия. Для определения модуля упругости материала при нормальных условиях использовались контактные экстензометры для изменения продольной деформации Epsilon.

В табл. 1 представлены результаты определения механических характеристик стандартных образцов материала УШ, изготовленных методом вакуумной инфузии

Physical and mechanical properties of carbon fiber reinforced plastic at normal conditions

Параметр	Направление армирования образцов	Направление нагружения относительно основы ткани	Климатические условия, температура, °С/ влажность, %	Результаты испытаний
Модуль упругости при растяжении, E 1	±45о	0о	+25±1 ° С/ 44-51 %	8342,61 МПа
Предел прочности при растяжении, X t	±45о	0о	+25±1 ° С/ 44-51 %	75,546 МПа
Предел прочности при сжатии, X c	±45о	0о	+25±1 ° С/ 44-51 %	62,595 МПа

• 1.3.    Модель материала в Digimat и ее верификация по результатам натурных испытаний

Для проведения вычислительного эксперимента необходимо определить актуальные механические характеристики материала. Для сокращения объема натурных механических испытаний определятся только модуль Юнга E 1 стандартного образца в направлении продольной оси УШ. В программе Digimat строится модель соответствующего материала [37], которая верифицируется по модулю E 1 . Далее в модуле Digimat-FE посредством создания представительного объема материала, включающего заданное распределение фаз (волокно и матрица) с их механическими характеристиками, гомогенизации методом конечных элементов и виртуального нагружения определяются все остальные механические характеристики.

На рис. 3 представлены этапы создания КЭ-модели представительного объема.

Задавались следующие геометрические характеристики плетения в меню построения геометрии модуля Digimat-FE в соответствии с технологией изготовления: тип плетения – Braiding; армирование – биаксиальное; угол плетения φ = 45°; ширина и высота жгута 2,8 и 0,3 мм соответственно; количество жгутов на сантиметр длины по основе и по утку – 3,5.

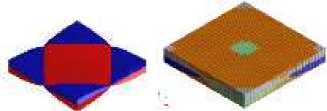
а                б                в

Рис. 3. Этапы создания КЭ-модели представительного объема композиционного материала УШ: а – модель плетения; б – представительный объем; в – КЭ-модель представительного объема

Fig. 3. Creation stages of the FE model of representative volume of the tape-spring hinge composite material: a – braiding model; b – representative volume; c –FE model of representative volume

В табл. 2–4 представлены свойства волокна, связующего и результаты расчета упругих характеристик для материала УШ. Прочностные характеристики определялись в натурных испытаниях в соответствии с п. 1.2.

Таблица 2

Характеристики волокна A49 [36]

Table2

Fiber Properties for A49 [36]

Характеристики	Значение
Линейная плотность	800tex
Диаметр	0,0071 мм
Объемную плотность	1,79 г/см3
Продольный модуль Юнга	240000 МПа
Модуль Юнга в плоскости волокна	14 375 МПа
Коэффициент Пуассона в плоскости волокна	0,2
Трансверсальный коэффициент Пуассона	0,0125
Трансверсальный модуль сдвига	4826 МПа

Таблица 3

Характеристики связующегоТ-26 [36]

Table 3

Matrix Properties for Т-26 [36]

Характеристики	Значение
Плотность	1,17 г/см3
Модуль Юнга	3100 МПа
Коэффициент Пуассона	0,4

Таблица 4

Механические характеристики материала, полученные методом гомогенизации в Digimat

Table 4

Mechanical properties of the material obtained by the homogenization method in Digimat

Обозначение	Описание	Значение
E 1 , МПа	Модуль упругости в направлении “1”	8843,10
E 2 , МПа	Модуль упругости в направлении “2”	8843,65
E 3 , МПа	Модуль упругости в направлении “3”	8649,30
µ 12	Коэффициент Пуассона в плоскости “1-2”	0,85

Окончание табл. 4

Обозначение	Описание	Значение
µ 21	Коэффициент Пуассона в плоскости “1-2”	0,85
µ 23	Коэффициент Пуассона в плоскости “2-3”	0,072
µ 32	Коэффициент Пуассона в плоскости “2-3”	0,070
µ 13	Коэффициент Пуассона в плоскости “1-3”	0,072
µ 31	Коэффициент Пуассона в плоскости “1-3”	0,070
G 12 , МПа	Модуль сдвига в плоскости “1-2”	20789,50
G 23 , МПа	Модуль сдвига в плоскости “2-3”	2256,76
G 13 , МПа	Модуль сдвига в плоскости “1-3”	2256,44
X t , МПа	Предел прочности при растяжении в направлении “1” образца	75,546
X c , МПа	Предел прочности при сжатии в направлении “1” образца	62,595
Y t , МПа	Предел прочности при растяжении в направлении “2” образца	75,546
Y c , МПа	Предел прочности при сжатии в направлении “2” образца	62,595

Различие между результатами определения модуля Юнга E 1 экспериментальным и расчетным методами составляет порядка 7 %. Можно сделать вывод, что определение упругих констант в Digimat проведено с достаточной точностью и их можно использовать для расчета конструкции шарнира, изготовленного из данного материала.

2.    Методика проведения испытаний упругого шарнира

Испытания образцов УШ проводились с использованием лабораторного стенда, спроектированного специально для данного вида исследования. При определении поля деформации в зоне складывания УШ при нормальных условиях использовалась бесконтактная система измерения деформации – VIC 3D.

Данный стенд (рис. 4) моделирует работу шарнира в условиях симметричного и несимметричного раскрытия конструкции и связанного с этим возможного скручивания плеч шарнира. Во всех случаях исследуется последовательность квазистатических состояний. Кроме того, данный стенд обеспечивает хорошую визуализацию процесса деформации шарнира, а также дискретную и непрерывную фотометрию.

Стенд предназначен для определения шарнирного момента при упругой деформации, связанной с заданными угловыми перемещениями плеч УШ, в том числе по двум осям (изгиб и скручивание), и связанных, в свою очередь, с ними полей деформации. Он позволяет провести ресурсные испытания образцов с фотометрией динамики изменений поля деформации и шарнирного момента от цикла к циклу.

На рис. 4 показан общий вид лабораторного стенда. Стенд был спроектирован и изготовлен на кафедре ПЛА КНИТУ-КАИ.

В качестве датчика определения деформации использовалась система фото- и видеофиксации, работающая по методике корреляции цифровых изображений (DIC – Digital Image Correlation) VIC 3D. Аппаратная часть системы представляет собой две цифровые камеры высокого разрешения, установленные в фиксированном положении. Программная часть позволяет визуализировать деформации в направлении оси УШ (положительные деформации – растяжение, отрицательные – сжатие).

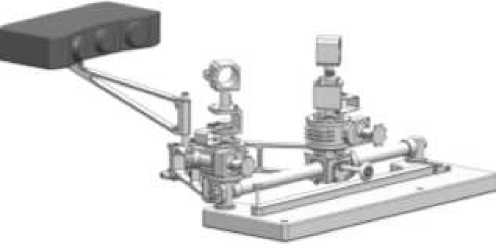
б

Рис. 4. Общий вид лабораторного стенда для определения упругих характеристик образцов УШ при изгибе: а – 3D-модель; б – общий вид с образцом

Fig. 4. Tailored bending test facility: a – 3D-model; b – general view with a specimen

Для определения деформационных характеристик образцов необходимо нанесение специальной графической сетки – спеклов. Визуализация работы расчетной программы VIC 3D представлена на рис. 5. Красный цвет обозначает максимальные положительные деформации, а розовый – максимальные отрицательные.

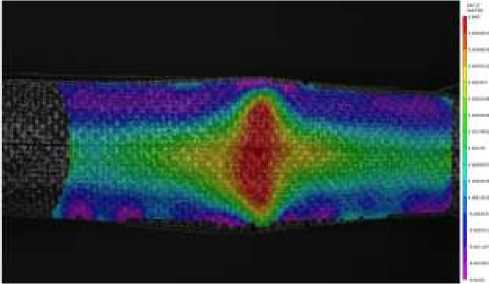
Рис. 5. Визуализация работы расчетной программы VIC 3D

Fig. 5. An image of bending deformation in VIC 3D simulations

В ходе эксперимента регистрировались: поле деформаций по всей поверхности образца, ε хх – деформация в направлении оси УШ, угол изгиба, шарнирный момент. Данный перечень характеристик был необходим для верификации расчетных моделей композиционных УШ для дальнейшего исследования влияния формы выреза и схемы армирования на шарнирный момент и прочность.

3.    Расчетные исследования деформирования и разрушения упругого шарнира 3.1.    Модели материалов и методика конечно-элементного моделирования

В качестве модели слоистого КМ может быть использована эквивалентная схема, когда одному плетеному монослою соответствуют последовательность из однонаправленных слоев с соответствующими углами армирования. Недостатком данного метода является отсутствие учета переплетения жгутов и изгиба волокна.

Другим методом, используемым в настоящей работе (см. п.1.3), является определение эффективных свойств плетеного монослоя путем создания репрезентативного объема КМ и гомогенизации свойств волокна и матрицы [37].

В качестве решателя для моделирования механического поведения УШ применялись неявный и явный методы анализа НДС, в процессе чего были выработаны рекомендации по их применению.

Применение неявного метода осуществлялось в системе ANSYS и позволяло провести квазистатический анализ с геометрической нелинейностью, определить НДС УШ при малом угле складывания и оценить прочность слоев по выбранному критерию прочности [38].

Достоинства неявного метода: автоматизация построения геометрической модели выреза; встроенные алгоритмы оптимизации конструкции с заданными ограничениями. К недостаткам неявного метода можно отнести: большое время расчета (порядка 500 часов) при малых углах без контактного взаимодействия, невозможность оценки прочности при больших углах складывания; большой шаг расчета до потери устойчивости; недостаточно точное определение нагрузки потери устойчивости шарнира.

Применение явного метода осуществлялось в системе LS-DYNA и позволяло смоделировать полное складывание и раскладывание и определить соответствующий момент, оценить прочность слоев по выбранному критерию прочности и предсказать разрушение [39].

Достоинства явного метода: возможность рассчитать полное складывание и раскладывание с прогрессирующим разрушением; малое время расчета (менее 0,5 часа); высокая точность определения максимального шарнирного момента.

Недостатки явного метода: отсутствие автоматизации расчетов и обработки результатов; необходимость доработки ключевого файла.

Для неявного метода решения в ANSYS Workbench в качестве критерия прочности были использованы критерий максимальных напряжений и критерий Пак 3D.

Основное соотношение для критерия максимальных напряжений

Величина т определяет касательные напряжения высокой нелинейности и представляется в виде соотношения

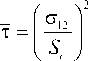
A = max

—n

XT

— 1

X C

^— 22   ^— 22

^, Y t  ^,   Y c

^— 12

S c

> 1.

¹ +2 ^{а G} 12 ^— 12

з Г

1 + ³ a G,,S 2

₂      12 c

Критерий прочности Пака строится на основе критерия Мора и включает форму разрушения волокна по превышению продольных напряжений в монослое, пределов прочности при растяжении и сжатии и несколько форм разрушения связующего.

Критерии максимальных напряжений и Пак 3D соответствуют нагрузке инициации разрушения монослоя («первое» разрушение). Под «первым» разрушением понимается превышения уровня напряжений по заданному критерию прочности в наиболее нагруженном слое.

В явном методе решения в LS-DYNA для анализа прочности использовалась модель материала MAT54 (MAT_ENHANCED_COMPOSITE_DAMAGE [39]), учитывающая отдельные типы разрушений волокна и матрицы материала:

для £ 11 >  0

(n..Y

• -¹¹   + Рт> 1 , E_x = E₂ = G_n = v₂₁=v₁₂ = 0;

• I X, J            ^{12   12   21   12}

3.2. Описание конечно-элементной модели

где а - коэффициент нелинейности, принимающий значения а = 0 и а >  0.

Модель материала MAT54 позволяет использовать дополнительные критерии по максимальным деформациям: DFAILT – растяжения вдоль волокон; DFAILC – сжатия вдоль волокон; DFAILM – растяжения и сжатия поперек волокон; DFAILS – сдвиговой. А также эффективную деформацию EFS, представляющую собой комплексный параметр, включающий деформации растяжения, сжатия и сдвига. Использование указанных критериев позволяет наиболее точно описать процесс разрушения высокомодульных композиционных материалов.

для —_n <  0

> 1, E = V 21 = V 12 = 0 ;

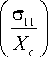
для —₂₂ >  0

22    + Pt >  1 , E₂ = v₂₁ = 0, G₁₂ = 0;

J для —22 < 0 (для 50% объема волокна)

В качестве конечных элементов (КЭ) модели выбираются оболочечные 4-узловые с формулировкой Belytschko-Tsay (SHELL181). Каждый оболочечный элемент имеет 12 степеней свободы в каждом узле: 3 компоненты вектора перемещений, 3 компоненты вектора скорости, 3 компоненты вектора ускорения в осях x , y , z срединной поверхности и 3 компоненты вектора вращения вокруг осей x , y , z .

Для обеспечения соответствия расчетной модели испытательной оснастке в качестве граничных условий (рис. 6) применены виртуальные шарниры. Каждый шарнир представляет собой виртуальное соединение точки с поверхностью. Точки расположены эквидистантно зонам поверхности закрепления шарнира. При этом шарниры имеют нулевые степени свободы – повороты ω y , ω z и перемещения u x , u y . Во избежание смещения модели как единого целого один из шарниров имеет нулевую компоненту перемещения u z .

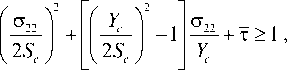
E 2 =V 21 =V 12 = 0, G 12 = 0, X_c = 2Y_C ,

ω x = –90°, ω y = ω z = 0°, u x = u y = 0

Рис. 6. Граничные условия

ω x = 90°, ω y = ω z = 0°, u x = u y = u z = 0

где X и Y – пределы прочности при растяжении вдоль и поперек образца КМ соответственно; X и Y – пределы прочности при сжатии вдоль и поперек образца КМ соответственно; S – предел прочности при

Fig. 6. Boundary conditions

сдвиге в слое; — _п , —₂₂, —₁₂ - напряжения в слое в осях ортотропии. Параметр Р определяет вклад касательных напряжений в разрушение при растяжении ( 0 <Р< 1).

Нагрузка задается путем поворота каждого из шарниров на заданный угол складывания ω x . Максимальный момент определяется реакцией в шарнире.

Размер конечного элемента выбран в соответствии с габаритами представительного объема, описанного в п. 1.3. Осредненные характеристики плетеного слоя, использованные в модели, представлены в табл. 4.

4.    Анализ результатов и выводы

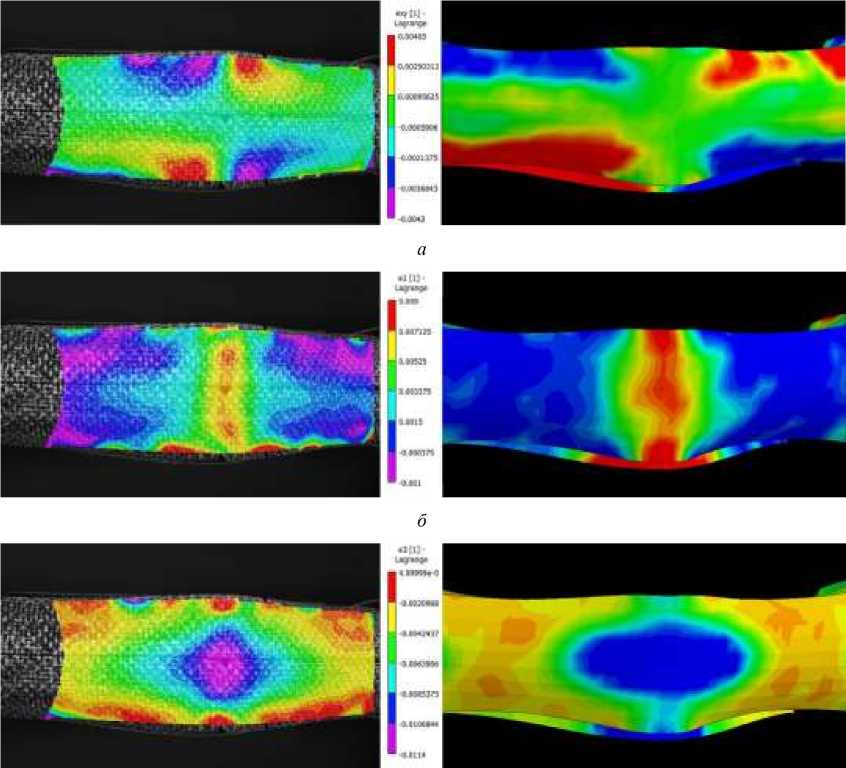
Для верификации расчетной модели было проведено сравнение полей деформаций и величины максимального шарнирного момента для угла складывания 172° после момента потери устойчивости, полученных экспериментально (рис. 7).

Для исследуемого УШ с конструктивными параметрами t = 0,6 мм, L = 204 мм, h = 23 мм, D = 30 мм на лабораторном стенде было получено значение максимального шарнирного момента 21,8 Н·м. Максимальный шарнирный момент, полученный в результате вычислительного эксперимента в LS-DYNA, составил 22,6 Н·м (рис. 8).

в

Рис. 7. Деформации шарнира вдоль оси (слева – VIC 3D, справа – LS-DYNA): а – сдвиговые деформации; б – максимальные главные деформации; в – минимальные главные деформации

Fig. 7. Tape-spring hinge deformations along the axis (on the left – VIC 3D, on the right – LS-DYNA): a – shear deformations; b – maximum principal deformations; c – minimal main deformations

Таким образом, численная модель показывает хорошую сходимость с результатами натурного эксперимента и может быть использована для определения рациональных конструктивных параметров УШ.

Для моделирования складывания и раскладывания на малый угол использовался неявный метод решения в ANSYS (рис. 9 и 10).

На рис. 9 представлена зависимость влияния диаметра «косточки» D при фиксированной ширине щели H = 15 мм и длине щели L =204 мм на величину максимального шарнирного момента M, Н∙м.

На рис. 10 представлена зависимость влияния ширины щели H при фиксированном диаметре «косточки» D = 30 мм и длине щели L = 204 мм на величину максимального шарнирного момента M, Н∙м.

Для моделирования полного складывания и раскладывания с целью сокращения времени расчета использовался явный метод решения в LS-DYNA (рис. 11 и 12).

На рис. 11 представлена зависимость влияния диаметра «косточки» D при фиксированной ширине щели H = 15 мм и длине щели L = 204 мм на величину максимального шарнирного момента M, Н∙м.

Н.ттур«ыП эксперимент

Вычнс.тительныЯ эксперпмеи!

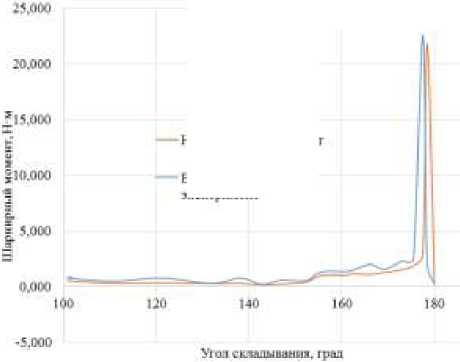
Рис. 8. Максимальный шарнирный момент

Fig. 8. Maximum hinge moment

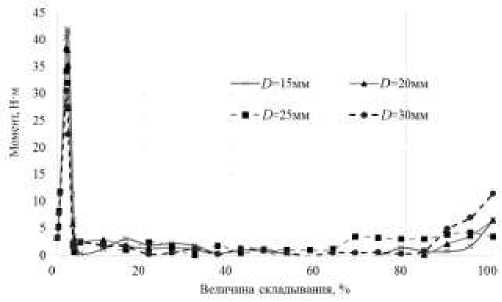
Рис. 11. Зависимость шарнирного момента от диаметра «косточки» ( H = 15 мм, L = 204 мм)

• Fig. 11.    Dependence of the hinge moment on the diameter ( H = 15 mm, L = 204 mm)

  

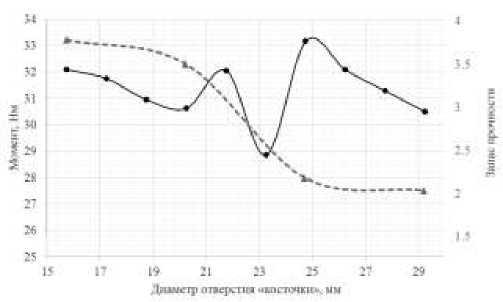
  Рис.9. Зависимость шарнирного момента и минимального запаса прочности по критерию Пака от диаметра «косточки» ( H = 15 мм, L = 204 мм)

  
  
  

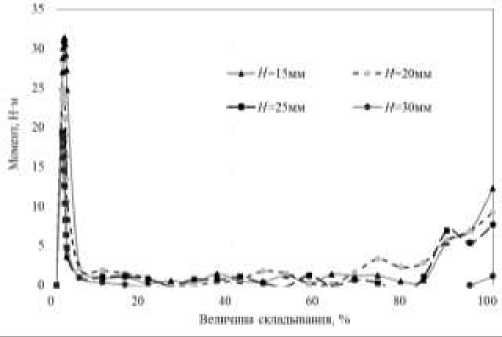
  Рис. 12. Зависимость шарнирного момента от ширины выреза ( D = 30 мм, L = 204 мм)

  
  

Fig. 9. Dependence of the hinge moment on the diameter ( H = 15 mm, L = 204 mm)

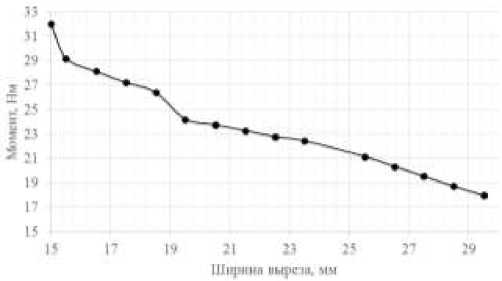
Рис. 10. Зависимость шарнирного момента от ширины выреза ( D = 30 мм, L = 204 мм)

Fig. 10. The dependence of the hinge moment on the width of the slit ( D = 30 mm, L = 204 mm)

На рис. 12 представлена зависимость влияния ширины щели H при фиксированном диаметре «косточек» D = 30 мм и длине щели L = 204 мм на величину максимального шарнирного момента M, Н∙м.

• Fig. 12.    The dependence of the hinge moment on the width of the slit ( D = 30 mm, L = 204 mm)

На рисунке 13 представлены результаты расчета УШ с H = 17 мм, L = 300 мм, D = 17 мм при разных углах плетения φ.

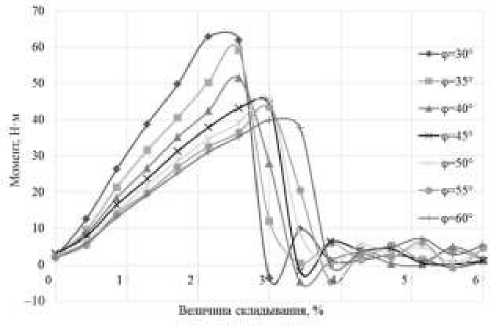
Рис. 13. Зависимость шарнирного момента от угла плетения φ

• Fig. 13.    The dependence of the hinge moment on the angle of braidingφ

На рис. 14 представлены результаты расчета прочности УШ с учетом прогрессирующего разрушения в LS-DYNA. Конструктивные параметры исследуемых УШ: с «прямым» вырезом при H = 12 мм, L = 300 мм, D = 12 мм; с вырезом в виде плавной «косточки» при H = 12 мм, L = 300 мм, D = 22 мм. Изменение формы выреза во втором случае позволяет снизить концентрацию напряжений в зоне радиусов скругления и спроектировать УШ, работающий без разрушения при полном складывании-раскладывании.

Рис.14. Результаты расчета УШ с учетом прогрессирующего разрушения в LS-Dyna

• Fig. 14.    The results of the calculation of the tape-spring hinge, taking into account progressive damage in LS-Dyna

На основании проведенных экспериментальных и численных исследований были сделаны следующие выводы:

• 1.    Использование эквивалентной схемы армирования позволяет определить упругие характеристики плетеного композита. При этом погрешность определения максимального момента составляет порядка 20%.

• 2.    Применение Digimat для виртуальных испытаний материалов позволяет сократить объем натурных испытаний и определить характеристики плетенного монослоя.

• 3.    Бесконтактная система измерения деформации VIC3D позволяет анализировать поля деформаций по всей исследуемой поверхности образца в реальном времени и проводить измерение деформации в заданных точках.

• 4.    Применение неявного решателя ANSYS в геометрически нелинейной постановке позволяет провести