Исследование метода оптимизации структурной идентификации динамических процессов в классе разностных уравнений заданного порядка

а для динамического процесса модель имеет вид

„ Ns

Ук = ^Рг ' Ч>$У^Ук-п’Ук-п+1’"-’Ук-1’^к-д+1’"-’^к-1’-^к^ *               (3)

с соответствующей выборкой данных

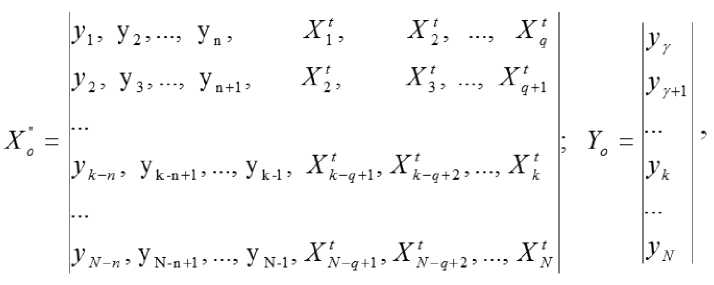
где

q, если q > n;

у = 5                  , y_k, к = 1..... N

[ и +1, если q

значение отклика объекта в k-й момент дискретного времени; Х_k – значение вектора параметров объекта в k -й момент дискретного времени, ( x_{k, j} – значение j -го параметра объекта в k-й момент дискретного времени); m – размерность пространства параметров объекта; N – объем выборки данных предыстории объекта; – операция транспонирования; и – наборы линейных и нелинейных функций с известными коэффициентами (параметрами) из некоторого заданного

упорядоченного множества допустимых структурных элементов; – вектор коэффициентов (параметров) модели; n – порядок разностного уравнения модели динамического объекта; Ns – число функций из некоторого за-

• 3.    Ns := Ns + 1;

• 4.    J_new := J ; {выполнить структурную идентификацию, J_new присвоить значение критерия структурной идентификации и запомнить s_new [ i ], i = 1, ..., Ns };

• 5.    если J > J d , то перейти на 8;

• 6.    J old := J new ; s ( i ):= s new [ i ], i =1, ..., Ns ;

• 7.    перейти на 3;

• 8.    Ns := Ns - 1;

• 9.    J := J_old ; {критерию структурной идентификации присвоить значение J_old , структура модели определена в s ( i ), i =1, ..., Ns };

• 10.    конец.

С целью уменьшения трудоемкости алгоритма структурной идентификации целесообразно не хранить матрицу X_F с функциями , k = 1, ..., Mz

данного упорядоченного множества допустимых структурных элементов, входящих в модель (априорно неизвестно); s [ i ] – индекс (номер) структурного элемента (функции k = 1, ..., Mz ) из заданного упорядоченного конечного множества допустимых структурных элементов; Mz – мощность (размерность) упорядоченного множества допустимых структурных элементов.

При известном порядке разностного уравнения модели динамического объекта и величине запаздывания по независимым входным переменным структурная идентификация статического (1) и динамического (3) объектов одинаковы, что позволяет использовать модель объекта вида (3). При неизвестном порядке разностного уравнения модели динамического объекта его можно определить, исследуя ряды разностей зависимой переменной.

При структурной идентификации по выборке данных предыстории процесса эффективны алгоритмы, удовлетворяющие двум базовым принципам [4]:

• 1.    принципу Геделя – только внешние критерии, основанные на новой информации, позволяют найти истинную модель объекта, скрытую в зашумленных данных;

• 2.    принципу Габора – всякая однорядная процедура структурной идентификации может быть заменена многорядной (обладающей меньшей трудоемкостью) только при условии сохранения «свободы выбора» нескольких лучших решений каждого предыдущего ряда.

Одним из наиболее широко применяемых на практике методов, удов-летворяющим этим принципам, является метод группового учета аргументов (МГУА), предполагающий использование внешних критериев, например критерия минимума смещения [4]. Метод МГУА решает задачу выбора Ns элементов из множества допустимых структурных элементов мощностью Mz , оптимизирующих выбранный критерий структурной идентификации.

В целом алгоритм структурной идентификации (с учетом принципов Геделя и Габора), минимизирующий значение критерия структурной идентификации, сводится к следующей последовательности действий:

• 1.    Ns := Ns_min ; {присвоить Ns минимально допустимое значение}

• 2.    J_old := J ; {выполнить структурную идентификацию, Jold присвоить значение критерия структурной идентификации и запомнить s [ i ], i = 1, ..., Ns }

^x^^x^.^^x^

9i (^2) 92 (^2) 9^ (^2)

F

91 №) 92 №) 9jtiz (^v)

а один раз вычислить и хранить меньшую по размерности нормальную матрицу Гаусса множества допустимых структурных элементов

N

-^^Zv.^a-tp/^a

z = Mz; i = 1, Mz,

,

С учетом симметричности относительно главной диагонали матрицы Q_F целесообразно хранить лишь ее верхний наддиагональный треугольник и главную диагональ. Также достаточно один раз вычислить и хранить вектор Z_F размерности Mz

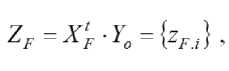
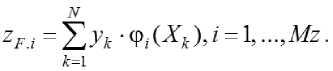
Под структурой модели будем понимать входящие в нее Ns конкретных структурных элементов в упорядоченном множестве допустимых структурных элементов { s [ i ]}, i = 1, ..., Ns . Если известна структура модели, то из матрицы Q_F и вектора Z_F можно сформировать нормальную матрицу Гаусса для модели с известной структурой

- ^Mj]

t

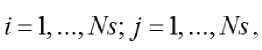
и соответствующий вектор ZS с элементами с использованием которых возможно определить вектор параметров P модели и критерии структурной идентификации

А—- О      О ' О      О '         D U

В выражении (8) матрица X_S структурно подобна матрице X_F, однако она содержит лишь столбцы функций

, i =1,..., Ns , k =1,..., N , принадлежащих модели с заданной структурой.

При использовании критерия минимума смещения выборка исходных данных (2), (4) делится на две подвыборки ( X_A , Y_A ) и ( X_B , Y_B ), например, на основе вероятностного критерия разбиения [5]. Искомое разделение исходной выборки на две подвыборки (их объемы N_A и N_B , N = N_A + N_B ) минимизирует отклонение функции распределения вероятности критерия для истинной модели от единичной функции и позволяет выбрать разделение с более острой зависимостью значения критерия от сложности модели ( Ns ) и достигаемым минимумом критерия более глубоким, чем при других возможных разделениях.

Критерий минимума смещения записывается в виде писать в виде

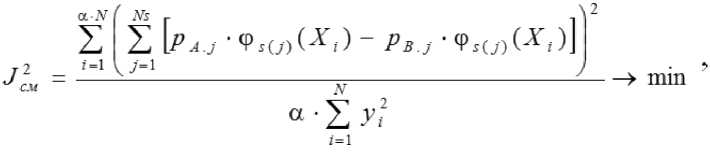
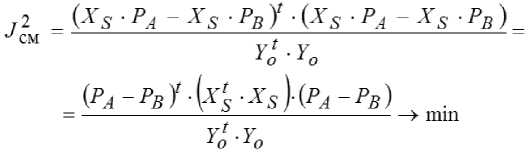
или

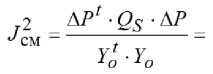
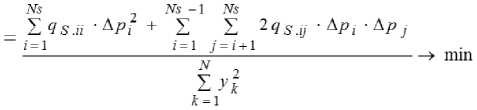
где △ P = PA - PB. Выражение '   1 х достаточ но вычислить один раз. Для каждой структуры необходи- мо определять параметры на обеих подвыборках (PA, PB) и формировать нормальную матрицу Гаусса QS из матрицы QF. Критерий регулярности отличается меньшей вычислительной сложностью, поскольку нормальную систему уравнений Гаусса приходиться решать только для подвыборки A, а на подвыборке B оценивается адекватность модели для задаваемой структуры. Критерий регулярности можно за-

где X_FA , X_FB – матрицы, подобные X_F , для подвыборок A и B ; X_SA , X_SB – матрицы, аналогичные матрице X_S , для подвыборок A и B ; Q_SA , Q_SB – нормальные матрицы Гаусса для моделей заданной структуры { s [ i ]}, i =1,..., Ns , получаемых на двух подвыборках A и B ; Z_SA , Z_SB – векторы, соответствующие вектору Z_S для подвыборок A и B ; P_A , P_B – векторы параметров для моделей заданной структуры, полученных на подвыборках A и B , с элементами p_A.i , p_B.i , i =1, ..., Ns ; α -коэффициент экстраполяции, α = 1.0 - 3.0, позволяющий описать дополнительные данные X_k , k = N +1,..., α N , которые определяет исследователь объекта в качестве потенциальной области их изменения.

С целью снижения трудоемкости вычисления критерия минимума смещения выражение (11) преобразуем к виду

N в (        Ns                   А

5 I У В.к - Z РАл -ф^Овл)

N в

Т. У В .к к = 1

где y_B.k – k -е значение зависимой переменной в подвыборке B ; X_B.k – k -й век-тор независимых переменных в подвыборке B ; p_A.i – i -й элемент вектора параметров, определенный на подвыборке A .

С целью снижения трудоемкости вычисления критерия регулярности выражение (13) преобразуем к виду

= (Уов - ^xsb -^рА У -^Хов - ^х sb -^ра) _

Уов УоВ

^NB           Ns               Ns                 Ns -1 Ns

Z У Вл "" ²'2 ²5Вл "  P Ал ⁺ 2 ЧВВЛ! ' Р Ал ^{+ 2} 2   2 Ч SB у ' Р Ал " Р A.J

_ 1 = 1              7 = 1                   7=1                       7 = 1 У = 7 + 1

-> min,

£ у вл

Таблица. Исследование состоятельности методики структурной идентификации

№ п/п	Уровень шума	ФПВ шума	ФПВ независимых входов модели	Точно ли синтезирована структура?
1	0	Нет ошибки	R (0, l )	Да
2			N (0, σ x )	Да
3			L (0, σ x )	Да
4	0.05 σ v	R (0, l )	N (0, σ x )	Да
5		N (0, σ v )		Да
6		L (0, σ v )		Да
7	0.1 σ v	R (0, l )	N (0, σ x )	Да
8		N (0, σ v )		Да
9		L (0, σ v )		Нет
10	0.2 σ v	R (0, l )	N (0, σ x )	Да
11		N (0, σ v )		Да
12		L (0, σ v )		Нет

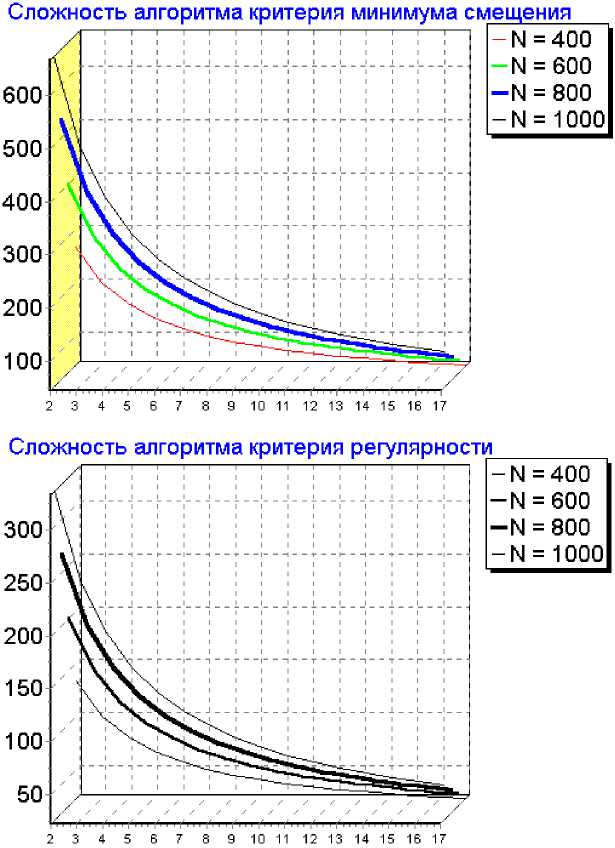
Рис.1 Исследование выигрыша в вычислительной сложности предложенных алгоритмов вычисления критериев минимума смещения и регулярности по сравнению с известными

где X_SA , X_SB – матрицы, соответствующие матрице X_S для подвыборок данных A и B ;

Алгоритм выбора наиболее информативных Ns структурных элементов из множества допустимых структурных элементов Mz [2] предполагает реализацию итерационной процедуры, позволяющей целенаправленно, с учетом результатов вычисления критерия структурной идентификации на каждой итерации, перейти от ситуации с равновероятным использованием в модели всех допустимых структурных элементов к ситуации, выявляющей искомые Ns структурных элементов.

Результат исследования состоятельности предложенной методики структурной идентификации представлен в таблице 1. Значения элементов матрицы независимых входов модели X_o (количество независимых входов 80, объем выборки данных предыстории процесса 1000) формировались на основе генерирования псевдослучайных чисел со следующими функциями плотности вероятностей (ФПВ): равномерное распределение R(0, l ), нормальное (Гауссово) распределение

N (0, σ _x ) и Лапласово распределение L (0, σ _x ). Двупараметрические распределения R (0, l ), N (0, σ _x ) и L (0, σ _x ) являются центрированными, т.е. их математическое ожидание равно нулю. Задавались вектор параметров и структура модели из 12 структурных элементов ( Ns = 12) в классе полиномов второго порядка. По выражению (2) расс _~ читывался вектор функционально зависимой переменной Y_o .

Уровень ошибки модели (столбец 2 таблицы) задавался следующим образом. Для одного из трех видов плотности распределения задавался параметр, характеризующий мощность шума ( l или σ ) ка ~ к долю стандартного отклонения зависимой переменной Y_o . Тогда вектор зависимой перем _~ ен-ной с учетом шума определяется по выражению Y_o = Y_o + E , где E = { ε _k }, k =1, …, Nw – вектор шума, генерируемый

датчиками псевдослучайных чисел с заданными законами распределения. Мощность шума увеличивалась до тех пор, пока точно определялась структура модели.

В строках 9 и 12 таблицы структура модели определяется неверно. В обоих случаях в структуру модели входит лишний структурный элемент (парное произведение) и структурные элементы задаваемые в экспе-рименте.

На рис. 1 представлен выигрыш в вычислительной сложности реализации критериев минимума смещения и регулярности по предложенной методике. Анализ выражений (11) – (14) показывает, что они содержат приблизительно одинаковое количество умножений и сложений. Выигрыш в вычислительной сложности определяется как отношение количества операций умножения (или сложения) при вычислении по предлагаемой методике критериев структурной идентификации к количеству операций умножения (или сложения) при вычислении по традиционной методике.

Например, для объема выборки данных предыстории процесса – 1000 измерений векторов независимых переменных и количества структурных элементов, входящих в модель, – 10 выигрыш в вычислительной сложности для критерия минимума смещения составляет 180 раз, а для критерия регулярности 90 раз.

Предлагаемый подход однократного вычисления Q_F и Z_F , формирования Q_S и Z_S , соответствующих различным структурам моделей, для вычисления параметров и критерия структурной идентификации при больших значениях N выборки данных значительно снижает трудоемкость алгоритмов структурной идентификации при использовании выборок данных большого объема. Методика использовалась при разработке программного обеспечения для осуществления структурной идентификации объектов на основе метода случайного поиска с адаптацией.