Исследование метода разреженных представлений для подавления эффекта ложного оконтуривания

Эффект ложного оконтуривания – это артефакт, который выражается в осцилляциях вблизи резких контуров на изображениях. Этот эффект возникает при искажении или потере высокочастотной информации на изображении и может появляться в результате работы алгоритмов обработки изображений, на изображениях магнитно-резонансной томографии, на изображениях, подвергнутых передаче через аналоговые каналы связи [1]. В основе этого эффекта лежит эффект Гиббса.

Алгоритмами, в результате которых может появиться эффект ложного оконтуривания, являются увеличение резкости изображения, подавление шума на изображении, повышение разрешения изображения. Наиболее часто встречающимся источником эффекта ложного оконтуривания является сжатие изображений и видео [2]. Пример изображения с эффектом ложного оконтуривания показан на рис. 1.

Рис. 1. Пример изображения с эффектом ложного оконтуривания

Существует множество различных методов обнаружения и подавления эффекта ложного оконтурива- ния для алгоритмов сжатия JPEG и JPEG 2000 [3–6]. С другой стороны, существует не так много алгоритмов, которые рассматривают задачи обнаружения и подавления чистого эффекта ложного оконтуривания с различными параметрами [7– 11]. Эти алгоритмы подавления основаны на связи эффекта ложного оконтуривания и полной вариации [12, 13], и их основная проблема заключается в том, что они, как правило, не отличают эффект ложного оконтуривания от мелких деталей на изображении, поэтому при обработке детали искажаются. Один из возможных алгоритмов, обходящих эту проблему, представлен в статье [14]. В данной работе мы представляем новый алгоритм подавления эффекта ложного оконтуривания, показывающий более качественные результаты при эффекте ложного оконтуривания высокой силы.

В работе для подавления эффекта ложного оконтуривания используется метод разреженных представлений, который в последнее время широко применяется как в задачах обработки сигналов [12, 15], так и в задачах обработки изображений [16]. Основная идея этого подхода заключается в построении представления исходных данных (в данном случае блоков изображения) в виде линейной комбинации небольшого числа сигналов из заранее выбранного избыточного словаря элементарных сигналов. В результате представление получается одновременно простым и информативным. Более подробно этот подход описан в параграфе 1.

В параграфе 2 проводится анализ взаимной согласованности сигналов и разреженности представлений для изображений с эффектом ложного оконтуривания, изображений с белым гауссовским шумом, а также размытых изображений [17]. По результатам этого анализа был разработан новый метод подавления эффекта ложного оконтуривания на изображениях, основанный на разреженных представлениях, который описывается в параграфе 3. Для улучшения ка- чества работы алгоритма на этапе обучения используется повышение резкости изображений алгоритмом деконволюции Винера–Ханта [18].

1.    Разреженные представления

Сформулируем задачу разреженных представлений для сигналов. При работе с изображениями мы также рассматриваем их как одномерные сигналы, для этого строки пикселей изображения записываются подряд в одномерный вектор.

Входной сигнал обозначим как вектор y , а словарь элементарных сигналов представим как матрицу D (записав элементарные сигналы по столбцам), тогда вектор представления c можно искать исходя из следующей задачи:

min || c ||0 при условии || y - Dc\ |2 < e , (1) где || c || 0 – количество ненулевых координат в векторе, ε – порог ошибки представления. В общем случае эта задача является NP-полной, но существуют алгоритмы приближенного решения этой задачи, на практике дающие хорошие результаты [15].

Один из таких алгоритмов – это алгоритм Orthogonal Matching Pursuit (OMP). Его идея заключается в последовательном жадном добавлении элементов к носителю решения. На каждом шаге выбирается такой элемент, чтобы приближение текущим набором элементов было наилучшим. В данной работе нами были также опробованы и другие алгоритмы решения задачи разреженных представлений, но алгоритм OMP дал наилучшие результаты. Поэтому везде далее при построении разреженных представлений используется этот метод.

Словарь задачи (1) может либо выбираться как заранее зафиксированный набор сигналов (например, базис дискретного косинусного преобразования) или же при помощи предварительного обучения на наборе сигналов, аналогичных входному. Второй способ обычно дает более качественные результаты, рассмотрим его подробнее.

Пусть матрица Y – набор сигналов для обучения, записанных в виде столбцов матрицы; матрица C – неизвестные представления этих сигналов (где i -й столбец этой матрицы равен c i ) и матрица D – искомый словарь. Тогда задача обучения словаря может формулироваться так:

min SI c l Io приусловии к ^- DC L <^e

D , C

i

Для этой задачи также существуют приближенные алгоритмы решения, один из которых – алгоритм K-SVD [15]. Этот алгоритм использует идею альтернативной итерации: задача поочередно решается относительно представлений C с фиксированным словарем D и относительно словаря D с фиксированным представлением C. В данной работе нами были также опробованы и другие алгоритмы решения задачи обучения словарей, но алгоритм K-SVD дал наилучшие результаты. Поэтому везде далее при построении словарей используется этот метод.

Алгоритмы вычисления представлений и построения словарей имеют высокую ресурсоемкость, кроме того, построение словарей также требует наличия большого набора обучающих сигналов. Поэтому при использовании этого подхода для изображений они, как правило, разбиваются на блоки небольшого размера (например, 8 × 8 пикселей), и все блоки рассматриваются независимо.

2.    Влияние искажений изображений на метод разреженных представлений

В методе разреженных представлений важную роль играет количество ненулевых коэффициентов в используемых представлениях [15]. Исследуем, как эффект ложного оконтуривания и другие искажения влияют на этот параметр. Помимо эффекта ложного оконтуривания, рассмотрим также размытие изображения и белый гауссовский шум. Дополнительно исследуем влияние повышения резкости методом Винера–Ханта, которое понадобится в параграфе 3 для улучшения предложенного метода.

Введем сначала понятие взаимной согласованности сигналов в методе разреженных представлений. Пусть x, y – два действительных вектора, тогда их взаимной согласованностью будем называть такую величину:

( x , y )

" * ^, y ) = HLI| y|

Пусть D – словарь со столбцами d 1, …, d m (они же элементарные сигналы), тогда взаимная согласованность словаря определяется так [19]:

ц ( D ) = max ц ( d , d ).

• * j            j

На практике, как правило, рост взаимной согласованности набора сигналов приводит к уменьшению оптимального количества ненулевых коэффициентов в представлениях для этого. Также наличие такой связи подтверждается тем, что в ряде теорем, связанных с разреженными представлениями, количество коэффициентов уменьшается с ростом взаимной согласованности словаря [19]. Например, единственность решения c в задаче (1) гарантируется при условии, что решение удовлетворяет такому свойству:

c |L < “ 1 + +—"—T

• 0 2 ( ц ( D ) J

Таким образом, мы в дальнейшем будем считать эти параметры обратными (и это будет подтверждено экспериментами). Далее мы приводим соображения, исходя из которых то или иное искажение должно увеличивать или уменьшать взаимную согласованность, и экспериментально подтверждаем предсказанное влияние искажений на взаимную согласованность и разреженность.

Пусть X, Y – независимые гауссовские вектора размерности n с независимыми компонентами. Тогда можно показать [20], что

E (ц( X , У )) = -C ^{Г (} n ^/T) .

(       ) 7ЛГ( (n +1)/2)

Эта функция является убывающей, а значит, при увеличении количества независимых компонент уменьшается взаимная согласованность и, следователь- но, растет количество коэффициентов в представлении. Модель независимых значений отдельных пикселей не совсем соответствует реальным изображениям, так как пиксели на изображении могут быть зависимыми (как правило, это верно для соседних пикселей). Тем не менее тенденция к уменьшению разреженности с увеличением числа компонент сохраняется.

Рассмотрим эффект ложного оконтуривания. Моделирование эффекта ложного оконтуривания происходит следующим образом. Введем параметр d и обозначим за l d маску , удаляющую все частоты вне круга радиуса w d = 1 / (2 d ):

• 1 1,    если , W 2 2 + w 2 <  w_d, xy d

la ⁽ w x , w y ) =2          ,------

• I 0,    если w _v + w „ >  w_d . xy d

Тогда с увеличением параметра d увеличивается и доля удаляемых частот, таким образом этот параметр отвечает за силу эффекта ложного оконтуривания.

Пусть I ( x , y ) – некоторое изображение. Тогда, обозначив операторы косинусного преобразования Фурье и обратного к нему как F и F ^-1 соответственно, введем оператор добавления эффекта ложного оконтуривания силы d :

R a ( I ) = F ^{- 1}( l a • F ( I )).

Это преобразование является ортогональным, поэтому сохраняет скалярное произведение, нормы и независимость векторов. В частотной области эффект ложного оконтуривания удаляет некоторое количество компонент, поэтому, по утверждению выше, взаимная согласованность должна увеличиваться и, следовательно, должна увеличиваться и разреженность [20].

Эффект размытия также может быть представлен как умножение преобразования Фурье изображения на некоторую маску. Например, в случае гауссовского размытия это будет функция Гаусса с центром в точке, соответствующей нулевой частоте. Эта функция значительно уменьшает коэффициенты для одной части частот и полностью обнуляет коэффициенты для другой части частот (с учетом квантования). То есть количество компонент уменьшается и, следовательно, взаимная согласованность и разреженность должны увеличиваться. В результате повышения резкости изображения взаимная согласованность и разреженность должны наоборот уменьшаться.

Рассмотрим теперь эффект добавления белого шума на примере гауссовского белого шума. Как было сказано выше, реальные изображения не совсем соответствуют модели независимых случайных компонент из-за связи между пикселями, и из-за этого взаимная согласованность для них в среднем выше, чем для случайных векторов. Однако при добавлении шума (который как раз является набором независимых компонент) связь между пикселями уменьшается и изображение становится более соответствующим модели с независимыми компонентами. Следовательно, взаимная согласованность должна уменьшаться, и количество коэффициентов должно расти.

Продемонстрируем теперь приведенные выше соображения с помощью численных экспериментов. Эксперименты производились на изображениях из базы [21].

Для демонстрации влияния различных искажений на взаимную согласованность изображений мы рассмотрели наборы случайных блоков изображений и посчитали среднюю взаимную согласованность для пар блоков из этого набора. Для каждого искажения мы рассмотрели различные значения силы искажения и построили график зависимости средней взаимной согласованности от силы искажения. Эти графики изображены на рис. 2–4 для эффекта ложного оконтуривания, размытия и шума соответственно. Видно, что для эффекта ложного оконтуривания и размытия взаимная согласованность растет с ростом силы искажения, а для шума наоборот убывает, что соответствует соображениям, описанным выше. Под силой искажения подразумевается доля удаляемых частот в случае эффекта ложного оконтуривания, степень размытия в случае размытия и сила шума в случае белого шума.

Средняя согласованность 0.7 0,6 0,5 0,4 0,3 0,2 0,1

° 1,5            2,0            2,5            3,0

Сила эффекта ложного оконтуривания d

Рис. 2. Изменение взаимной согласованности при добавлении эффекта ложного оконтуривания; пунктиром обозначено значение взаимной согласованности для обычных изображений, а сплошной линией – для изображений с различной силой d эффекта

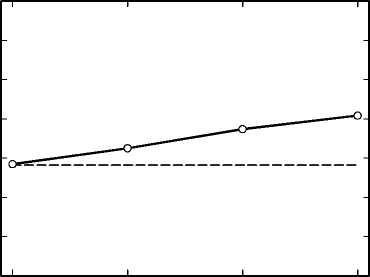
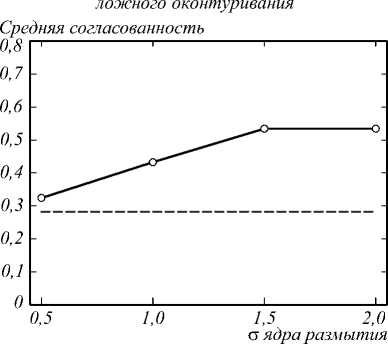
Рис. 3. Изменение взаимной согласованности при добавлении размытия; пунктиром обозначено значение взаимной согласованности для обычных изображений, а сплошной линией – для изображений с различной силой размытия

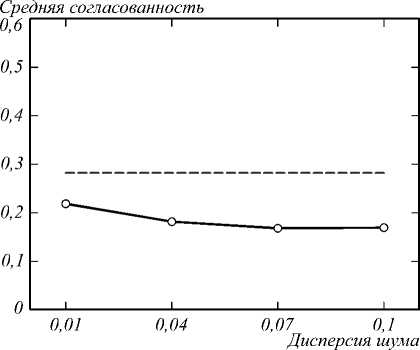
Рис. 4. Изменение взаимной согласованности при добавлении шума; пунктиром обозначено значение взаимной согласованности для обычных изображений, а сплошной линией – для изображений с различной дисперсией шума (считая, что яркость принимает значения от 0 до 1)

Для оценки подходящей степени разреженности для естественных изображений или изображений с одним из рассматриваемых искажений мы используем обучение словарей на выборке блоков изображений рассматриваемого типа и вычисляем среднюю разреженность по всем представлениям блоков обучающей выборки. Полученная величина зависит не только от типа сигнала, но и от ошибки ε, поэтому мы проводим обучение при различных значениях ошибки и строим зависимость разреженности от ошибки. Таким образом, характеристикой разреженности для данного типа и силы искажения является график зависимости разреженности от ошибки ε. Ошибка ε приводится в терминах метрики PSNR, которая вычисляется по формуле:

PSNR = 10log10 (MAXI /MSE), где MAXI – максимальное значение, принимаемое пикселями на изображении, и MSE – среднеквадратичная ошибка.

Графики зависимости ошибки от разреженности изображены на рис. 5 –7. Видно, что для эффекта ложного оконтуривания и размытия количество коэффициентов растет с ростом силы искажения, а для шума наоборот убывает, что соответствует соображениям, описанным выше.

На рис. 8 изображены графики разреженности представлений для блоков обычных изображений, изображений с эффектом ложного оконтуривания, а также изображений с эффектом ложного оконтуривания после повышения резкости методом деконволюции Винера–Ханта. Видно, что повышение резкости повышает количество необходимых коэффициентов.

3.    Подавление эффекта ложного оконтуривания

В работе [14] был предложен метод подавления эффекта ложного оконтуривания на основе разреженных представлений, и в этом методе на этапе обучения строился словарь одновременно для изображений с эффектом ложного оконтуривания и изображений без него (далее будем обозначать этот метод как JC – joint coding).

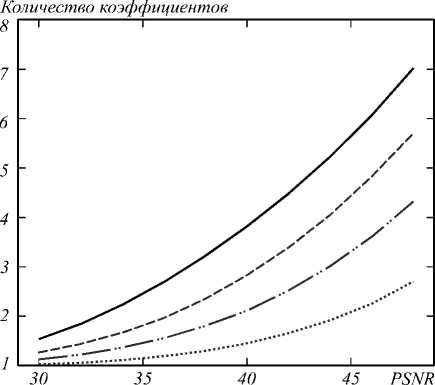
Рис. 5. Изменение разреженности при добавлении эффекта ложного оконтуривания; сплошная линия соответствует изображениям без искажения, штриховая, штрихпунктирная и точечная соответствуют изображениям с эффектом ложного оконтуривания с силой искажения d = 1,5; 2; 3 соответственно

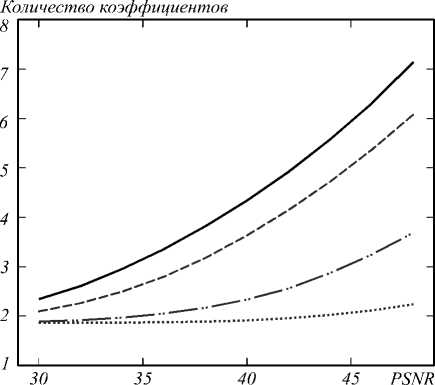
Рис. 6. Изменение разреженности при добавлении размытия; сплошная линия соответствует изображениям без искажения, штриховая, штрихпунктирная и точечная соответствуют изображениям с размытием с ядром с σ = 0,5; 1; 2 соответственно

На этапе применения алгоритма он работал только с изображениями с эффектом ложного оконтуривания, и было обнаружено, что оптимальные параметры разреженности при обучении и применении метода сильно отличались.

Мы полагаем, что такой эффект был связан с тем, что для применения метода разреженных представлений к обычным изображениям и изображениям с эффектом ложного оконтуривания необходимо использовать различную степень разреженности (как было показано в параграфе 2).

Далее представлен новый алгоритм подавления эффекта ложного оконтуривания, основанный на ме- тоде разреженных представлений. В нем словари для обычных изображений и изображений с эффектом ложного оконтуривания обучаются отдельно, таким образом решая проблему, описанную выше.

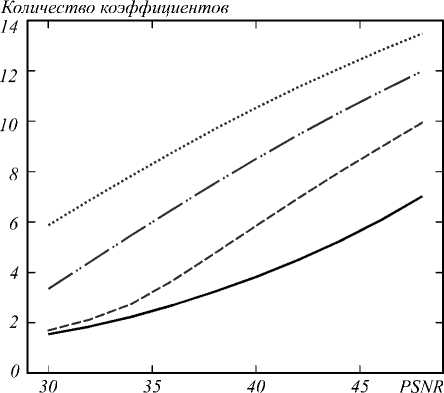
Рис. 7. Изменение разреженности при добавлении шума; сплошная линия соответствует изображениям без искажения, штриховая, штрихпунктирная и точечная соответствуют изображениям с шумом дисперсией 0,02; 0,05; 0,1 соответственно

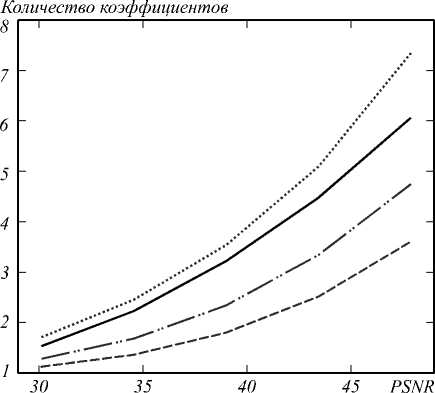
Рис. 8. Изменение разреженности при повышении резкости; сплошная линия соответствует изображениям без искажения, штриховая соответствует изображению с эффектом ложного оконтуривания с силой искажения, равной 2, штрихпунктирная и точечная соответствуют предыдущим изображениям с дополнительным повышением резкости с гауссовским ядром с σ, равным 1 и 1,5 соответственно

Опишем алгоритм более детально. Для обработки каждого блока алгоритм использует два заранее обученных словаря.

Первый словарь D 1 моделирует изображения без эффекта ложного оконтуривания и обучается на любом наборе блоков естественных изображений.

Второй словарь D2 моделирует чистый эффект ложного оконтуривания. Для его обучения мы используем разницу между изображением с искус- ственно созданным эффектом ложного оконтуривания и соответствующим исходным изображением.

Эффект ложного оконтуривания наиболее выражен вблизи резких контуров на изображении. Введем обозначения областей Basic Edge Neighborhood (BEN) и Basic Edge Points (BEP) [1, 9]. Для построения этих областей на изображении находятся ярко выраженные контуры, отстоящие достаточно далеко от других контуров (во избежание интерференции эффекта ложного оконтуривания). Области, соответствующие точкам контура, обозначаются BEP, а области на небольшом расстоянии от них обозначаются BEN. На рис. 9 схематически изображены эти области.

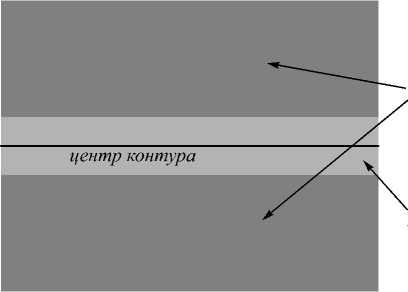
Рис. 9. Области BEN и BEP

Для улучшения качества обучения словаря D 2 мы обучаем его только на блоках, взятых из областей BEN, так как в этих областях находятся наиболее выраженные осцилляции. Такое ограничение значительно уменьшает размер обучающий выборки. Однако эффект ложного оконтуривания инвариантен к поворотам, поэтому вместе с каждым изображением в выборке можно рассматривать и его повернутые версии. Это позволяет искусственно расширять размер обучающей выборки. Нами рассматривались повороты на 90°, 180° и 270° во избежание ошибок интерполяции.

Из двух описанных выше словарей D 1 и D 2 составляется словарь D = [ D 1 ; D 2 ], получаемый объединением множества элементарных сигналов этих словарей (столбцы соответствуют сигналам). Далее для входного изображения y строится разреженное представление c = [ c 1 ; c 2 ] по объединенному словарю:

min || c ||0 при условии ||_ y - Dc |2 < e .

Тогда

Dc = D 1 c 1 + D 2 c 2 .

Обозначим y1 – искомое изображение без эффекта ложного оконтуривания, тогда y = y1 + y2, где y2 – изображение с чистым эффектом ложного оконтуривания. При построении представления c алгоритм использует элементарные сигналы из обоих словарей, причем требование на минимальность количества использованных сигналов приводит к тому, что эти сигналы используются наиболее эффективно. Поэтому для восстановления y1, как правило, используются элементарные сигналы словаря D1, а для восстанов- ления y2 – элементарные сигналы словаря D2. Исходя из этого положим y1 ≈ D1c1.

Мы также обнаружили, что повышение резкости изображений с эффектом ложного оконтуривания при обучении словаря D 2 позволяет увеличить эффективность метода. Для повышения резкости используется алгоритм деконволюции Винера–Ханта. Мы полагаем, что это связано с тем, что повышение резкости позволяет увеличить количество коэффициентов в представлениях для этого словаря и таким образом сбалансировать количество коэффициентов на этапе тестирования (это приводит к тому, что для словарей D 1 и D 2 нужна примерно одинаковая разреженность). Кроме этого, такой эффект может также достигаться за счет того, что повышение резкости усиливает эффект ложного оконтуривания на изображении, и на этапе обучения это позволяет алгоритму лучше настроиться на отделение эффекта ложного оконтуривания от элементов обычных изображений.

Для тестирования эффективности метода мы использовали базу изображений [21]. На этих изображениях был смоделирован эффект ложного оконтуривания в соответствии с описанием в параграфе 2, также для соответствия реальному эффекту ложного оконтуривания на них был добавлен небольшой шум. Изображения были поделены на две группы – для обучения и для тестирования. Оценка эффективности метода производилась по трем различным метрикам (в сравнении изображений после восстановления и исходного изображения): PSNR, вычисленный глобально по всему изображению, PSNR в области BEP и PSNR в области BEN.

Тестирование проводилось при различных значениях d . Для сравнения использовались результаты метода JC и метода, основанного на полной вариации [9] (далее обозначим его TV – total variation). При сравнении глобального значения PSNR было обнаружено, при низких значениях d = 1,5, 2 метод JC дает наилучшее качество, а при более высоких значениях d = 2,5, 3 качество метода JC и предложенного метода близки (результаты в сравнении с методом TV аналогичны [14]). В табл. 1 приведено сравнение значений PSNR в области BEN, а в табл. 2 – сравнение значений PSNR в области BEP.

Табл. 1. Сравнение метода TV, метода JC и предложенного метода в терминах метрики PSNR в области BEN, жирным выделен наилучший результат в строке

d	TV	JC	Предложенный
1,5	35,79	36,16	35,62
2	34,5	34,24	34,61
2,5	33,62	33,05	33,65
3	32,64	31,36	32,78

Исходя из полученных результатов можно сделать следующие выводы. Метод JC показывает хорошие результаты по глобальному значению PSNR для всех значений d. Однако в областях BEN и BEP его результаты хуже, чем результаты метода TV и предложенного метода. Это связано с тем, что метод TV в основном ориентирован на работу с текстурами, ко- торые не обязательно расположены вблизи контуров. Предложенный метод показывает хорошие результаты по глобальному значению PSNR для высоких значений d, а также превосходит методы TV и JC по значению PSNR в областях BEN и BEP.

Табл. 2. Сравнение метода TV, метода JC и предложенного метода в терминах метрики PSNR в области BEP, жирным выделен наилучший результат в строке

d	TV	JC	Предложенный
1,5	32,29	32,27	31,45
2	29,12	29,04	29,26
2,5	26,92	26,85	27,06
3	25,36	25,2	25,43

Мы полагаем, тот факт, что предложенный метод хорошо работает при больших значениях d, связан с тем, что, во-первых, он работает с блоками изображений большего размера (для метода JC это было невозможно из-за высокой вычислительной сложности), а ширина осцилляций и области, где эффект ложного оконтуривания заметен, растет с увеличением значения d. Во-вторых, эффект, описанный в параграфе 2, также сильнее выражен при более высоких значениях d.

На рис. 10 приведен фрагмент изображения с эффектом ложного оконтуривания для d = 2,5 . На рис. 11 приведен аналогичный фрагмент изображения после подавления эффекта ложного оконтуривания методом JC, а на рис. 12 – с использованием предложенного метода. Видно, что в некоторых областях вблизи границ новый метод лучше устраняет арте-фактные осцилляции.

Рис. 10. Изображение с эффектом ложного оконтуривания (d = 2,5) для применения алгоритма подавления

Полный алгоритм подавления эффекта ложного оконтуривания устроен следующим образом. Предварительно необходимо обучить несколько словарей для эффекта ложного оконтуривания разной силы.

Рис. 11. Изображение после подавления эффекта ложного оконтуривания методом JC (d = 2,5)

Рис. 12. Изображение после подавления эффекта ложного оконтуривания предложенным методом (d = 2,5)

Для входного изображения сначала определяется степень размытия контуров σ на изображении [1]. В работе [8] было показано, что степень размытия контуров σ линейно зависит от силы ложного оконтуривания d . Для этого для набора контуров с различными значениями d находилось приближение этого контура размытым контуром, дающее наименьшую ошибку, и было показано, что зависимость силы размытия σ от силы эффекта ложного оконтуривания d хорошо приближается формулой σ = 0,336 d . Таким образом, после получения силы размытия σ можно вычислить силу эффекта ложного оконтуривания как d = σ / 0,336. С помощью оцененных параметров далее выбирается наиболее подходящий словарь, и с его помощью производится подавление эффекта ложного оконтуривания.

Заключение

В статье проведен анализ влияния различных искажений изображений на необходимое количество ненулевых коэффициентов в методе разреженных представлений. В целом это влияние можно сформулировать следующим образом: искажения, делающие изображения менее похожими на случайные (то есть увеличивающие межпиксельную корреляцию), уменьшают количество необходимых коэффициентов, а искажения, делающие изображения более похожими на случайные (то есть уменьшающие межпиксельную корреляцию), увеличивают количество необходимых коэффициентов.

Был предложен новый метод подавления эффекта ложного оконтуривания, основанный на разреженных представлениях. Метод был разработан на основе приведенного анализа влияния искажений на необходимое количество ненулевых коэффициентов в методе разреженных представлений. Было показано, что метод дает хорошие результаты для высоких значений силы ложного оконтуривания. Наиболее ярко выражено улучшение в областях вблизи контуров изображений.

Работа выполнена при поддержке гранта Российского научного фонда, проект № 14–11–00308.

Для выполнения численных экспериментов в работе использовались библиотеки SciPy [22], Mat-plotlib [23] и Scikit-learn [24] для языка Python.