Исследование методом ЯМР функции распределения ферромагнитных наночастиц в коллоидном растворе по значениям их магнитных моментов

Магнитный момент Р наночастицы в магнитной жидкости является важной характеристикой, определяющей ее магнитные свойства. Его можно измерить по наклону начального и конечного участков кривой намагничивания [1]. Однако если в жидкости имеется дисперсия магнитных моментов наночастиц, то результат таких измерений становится неоднозначным. При этом наиболее полную информацию о магнитных моментах наночастиц дает функция распределения наночастиц по значениям их магнитных моментов f(P). Методов экспериментального определения функции f(P) в настоящее время не существует. Имеются работы, в которых f(P) задают эмпирически в виде логнормальной или гамма-функции с несколькими неизвестными параметрами, которые определяют, рассчитывая с учетом f(P) кривую намагничивания и сравнивая расчетную кривую с экспериментальной. При таком подходе полученная функция f(P) является субъективной, т. к. ее вид зависит от выбранной модели межчастичных взаимодействий. Для того чтобы функция распределения была объективной, ее нужно определять экспериментально. В работе [2] был предложен метод определения магнитного момента наночастиц в магнитной жидкости методом ЯМР по двум экспериментальным точкам кривой намагничивания, одна из которых выбирается в начале кривой, где выполняется закон Кюри, а вторая в средней части кривой, где закон Кюри не выполняется. Проверка метода показала, что при малой дисперсии магнитных моментов наночастиц независимо от выбранной второй точки кривой намагничивания он дает практически одно и то же значение Р. Однако при наличии в магнитной жидкости заметной дисперсии магнитных моментов наночастиц полученные с помощью предложенного метода значения Р зависят от выбранной второй точки кривой намагничивания. Настоящая работа посвящена исследованию возможностей использования этой зависимости для определения функции распределения наночастиц по величинам их магнитных моментов.

ЭКСПЕРИМЕНТ

Экспериментальная установка аналогична описанной в работе [1]. Исследуемая магнитная жидкость заполняет два цилиндрических контейнера, расположенные нормально индукции внешнего магнитного поля В 0 на расстоянии 3 мм друг от друга. В щели между контейнерами и вблизи боковой поверхности одного из них помещены датчики ЯМР (датчики нутации [3]) для измерения соответственно напряженности Н и индукции В магнитного поля внутри магнитной жидкости. Для определения магнитного момента наночастиц Р выбирают две точки кривой намагничивания. Первую точку выбирают при малой индукции внешнего магнитного поля В 0 , на начальном участке кривой намагничивания, где выполняется закон Кюри. Датчиками ЯМР измеряют напряженность Н 1 и индукцию В 1 магнитного поля внутри жидкости, определяют напряженность намагничивающего поля Н н1 = ( В 1 / µ 0 ) и находят начальную магнитную восприимчивость æ 1 = (1 – ( Н 1 / Н н1 )), которая связана с намагниченностью насыщения жидкости и магнитным моментом наночастиц выражением

Рис. 1. Теоретическая зависимость параметра α и функции Ланжевена от параметра ξ

æ1 = Мн Р µ0 / 3кТ. Вторую точку кривой намагничивания выбирают на участке с большей индукцией внешнего магнитного поля В0, где закон Кюри не выполняется. Датчиками ЯМР измеряют напряженность Н2 и индукцию В2 магнитного поля внутри жидкости, находят напряженность намагничивающего поля Нн2 = (В2/µ0) и определяют магнитную восприимчивость æ2 = (1 – (Н2/Нн2)), которая связана с намагниченностью насыщения жидкости и магнитным моментом наночастиц выражением æ2 = Мн La(ξ2)/Нн2, где La(ξ2) — функция Ланжевена, ξ2 = (Р µ0 Нн2/кТ) — параметр Ланже-вена в выбранной второй точке кривой намагничивания. Отношение магнитных восприимчиво-стей обозначим символом α. Этот параметр зависит от ξ2: α(ξ2) = æ2/æ1 = 3 La(ξ2) / ξ2 — поэтому, определив из опыта α, можно найти ξ2. Расчетные зависимости параметра α и функции La от ξ при- ведены на графике рис. 1. Определив из графика рис. 1 соответствующее полученному экспериментально параметру α значение ξ2, находим магнитный момент Р = ξ2 кТ / µ0 Нн2, а определив из этого же графика значение функции Ланжевена La(ξ2), находим намагниченность насыщения Мн = = М2 / La(ξ2). В качестве объектов исследования для сравнения были применены две магнитные жидкости. Жидкость 1 — ранее исследованная в работах [1, 2], у которой не было заметного различия магнитных моментов, измеренных на начальном и конечном участках кривой намагничивания, что говорит о малой дисперсии, и специально приготовленная магнитная жидкость 2, у которой эти магнитные моменты заметно различались, что говорит о большой дисперсии. На рис. 2, 3 приведены зависимости полученных по двум точкам кривой намагничивания значений магнитных моментов наночастиц и намагниченностей насыщения жидкостей от напряженности намагничивающего поля Нн2 в выбранной точке 2. Видно, что с ростом Нн2 измеренные значения Р уменьшаются, а измеренные значения Мн увеличиваются. Для жидкости 1 относительные различия измеренных значений Мн и Р составляют соответственно 20 % и 26 %, а для жидкости 2 соответственно 50 % и 75 %, т. е. в 2.5 раза больше. Большая зависимость Мн и Р от Нн2 у жидкости 2 подтверждает, что она вызвана дисперсией магнитных моментов наночастиц. Это дает предпосылку по различию значений Р и Мн, полученных при разных напряженностях поля Нн2, оценивать дисперсию магнитных моментов наночастиц в магнитной жидкости.

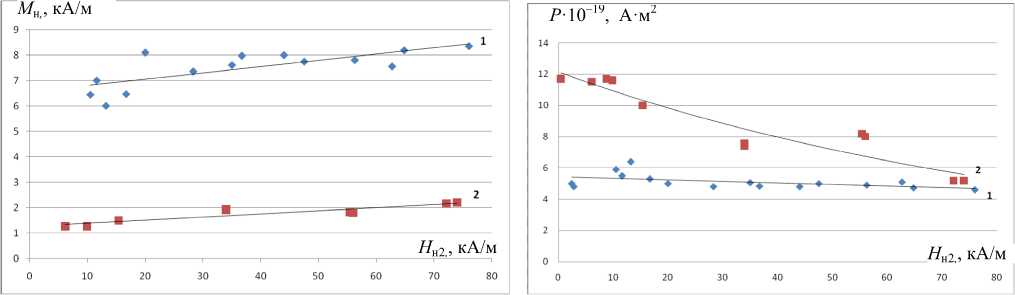
Рис. 2. Экспериментальные зависимости измеренных предлагаемым методом значений М _н от напряженности намагничивающего поля Н н2 в выбранной второй точке кривой намагничивания. Кривая 1 — жидкость 1; кривая 2 — жидкость 2

Рис. 3. Экспериментальные зависимости измеренных значений Р от напряженности намагничивающего поля Н н2 в выбранной второй точке кривой намагничивания. Кривая 1 — жидкость 1; кривая 2 — жидкость 2

ОБЪЯСНЕНИЕ ВЛИЯНИЯ ДИСПЕРСИИ МАГНИТНЫХ МОМЕНТОВ

НАНОЧАСТИЦ НА ВИД КРИВЫХ, ПРИВЕДЕННЫХ НА РИС. 2 И 3

Предположим, что в растворе есть два сорта наночастиц: частицы 1 с большим магнитным моментом Р1 и частицы 2 с меньшим магнитным моментом Р2, — создающих близкие по величине намагниченности насыщения Мн1 и Мн2. Частицы 1 имеют кривую намагничивания, расположенную левее, чем кривая частиц 2, поэтому на начальном участке кривой намагничивания раствора вклад в суммарную намагниченность М = М1 + М2 больше от частиц 1, а на участке кривой ближе к насыщению вклады от частиц 1 и 2 сближаются. В связи с этим определения магнитного момента Р по намагниченностям М с использованием вторых точек, расположенных на разных участках кривой намагничивания, дают разный результат: при увеличении напряженности Нн2 измеряемое значение Р уменьшается от Рмакс ≈ Р1 до Рмин ≈ (Р1+ Р2)/2. При использовании двух точек кривой намагничивания намагниченность насыщения находится по формуле Мн = М / La(ξ). В левой части кривой намагничивания намагниченность М создается преимущественно частицами с Р1, у которых при заданной напряженности Нн2 значения ξ и La(ξ) больше, а вклад в намагниченность частиц с Р2 меньше, т. к. у них значения ξ и La(ξ) меньше, поэтому измеряемое значение Мн ≈ М1 меньше истинного значения Мн = Мн1 + Мн2. С ростом Нн2 значения La(ξ1) и La(ξ2) сближаются, приближаясь к 1, поэтому вклад в Мн частиц с Р2 приближается к вкладу частиц с Р1 и измеряемое значение Мн приближается к значению Мн1 + Мн2. Таким образом, с ростом напряженности магнитного поля Нн2 измеряемая по двум точкам кривой намагниченность насыщения меняется от минимального зна- чения Мн,мин ≈ Мн1 до максимального значения Мн,макс ≈ Мн1 + Мн2. Значит, рост измеряемого значения Мн с ростом Нн2 характеризует вклад в намагниченность насыщения жидкости частиц с малым магнитным моментом (М,н,макc – Мн,мин) ≈ М2. В рассматриваемой модели количества частиц с магнитными моментами Р1 и Р2 — N1 = (Мн1 / Р1) и N2 = (Мн2 / Р2). Поэтому, используя полученные экспериментально результаты, эти величины можно оценивать по формулам: N1 = Мн,мин / Р1, N2= (Мн,макс– Мн,мин) / Р2.

ОПРЕДЕЛЕНИЕ ВИДА ФУНКЦИИ РАСПРЕДЕЛЕНИЯ ЧАСТИЦ ПО МАГНИТНЫМ МОМЕНТАМ

При непрерывном распределении частиц по значениям Р функция распределения f ( P ) = d N /d P , где d N ( P ) — число частиц c магнитным моментом от Р до Р + d Р . Используя связь d N = d М н / P , можно написать

f ( P ) = (d M н / d P ) / P.            (1)

Определяемые в выбранной второй точке кривой намагничивания значения намагниченности насыщения М н и магнитного момента Р однозначно связаны между собой, т. к. они рассчитываются по одним и тем же значениям æ 1 , æ 2 , Н н2 , ξ 2 . Поэтому их производная является однозначной. Из экспериментальных зависимостей, представленных на рис. 4, 5, видно, что в исследованном диапазоне магнитных моментов у обеих жидкостей производные d M н / d P от Р практически не зависят. Поэтому в выражении (1) производную d M н / d P можно заменить на коэффициент K . В результате получаем функцию распределения:

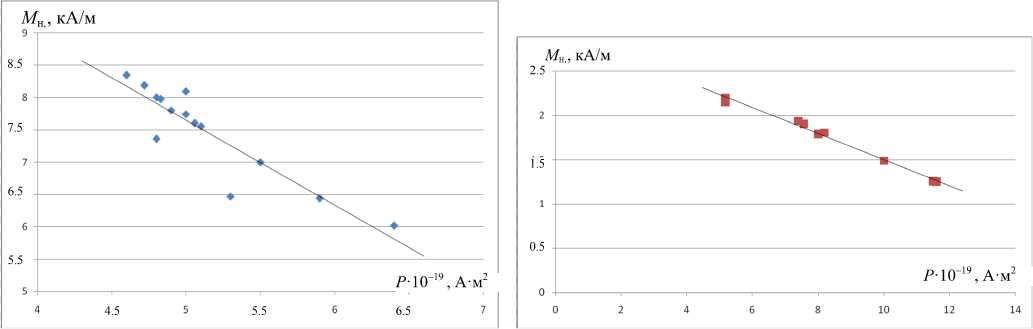
Рис. 5. Экспериментальная зависимость измеренных значений М _н от измеренных значений Р для жидкости 2

Рис. 4. Экспериментальная зависимость измеренных значений Мн от измеренных значений Р для жидкости 1

f ( P ) = K / Р ,                   (2),

где коэффициент K должен удовлетворять условию нормировки f (P W = 1.

г P макс j PMUH

Подставив f ( P ) из (2) и произведя интегрирование, получаем K ln( P макс / P мин ) = 1, откуда K = (ln( P макс / P мин ))^–1. В результате функция распределения:

f ( P )=—

P ln

' P макс

P мин

ОПРЕДЕЛЕНИЕ СРЕДНЕГО МАГНИТНОГО МОМЕНТА И КОНЦЕНТРАЦИИ НАНОЧАСТИЦ С МАГНИТНЫМИ МОМЕНТАМИ В ДИАПАЗОНЕ 4.5·10^–19<  Р < 12·10^–19А∙м²

Используя функцию распределения (3), можно найти выражение для среднего значения магнитного момента

rP макс

Pp -jp мин

P

P • f ( P )d P = J макс

P мин

( ln

V

(P макс

P

V мин

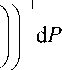
(P макс

P ) мин

(P ln макс

P

V J мин

Пользуясь выражением (4), из графиков рис. 3 находим Р ср . Для жидкости 1 получаем Р ср = (5.5 – – 4.8) / ln(5.5 / 4.8) = 5.14·10^–19 А·м². Это значение не противоречит полученному в работе [1] по наклону начального и конечного участков кривой намагничивания. Для жидкости 2 получаем Р ср = (12 – 5.3) / ln(12 / 5.3) = 8.2·10^–19 А·м². Концентрацию магнитных наночастиц можно оценить по формуле N = M н,макс / Р ср , взяв значения М н,макс из рис. 2. Для жидкости 1 получаем N = = 8.2·10³ / 5.14·10^–19 = 1.6·10²² м^–1, для жидкости 2 получаем N = 2.2·10³/ 8.2·10^–19= 0.27·10²² м^–1.

чений Р (4.5·10^–19<  Р < 12·10^–19 А·м²) она пропорциональна 1 / Р , т. е. уменьшается при увеличении Р . Сравним полученный результат с экспериментальными функциями распределения наночастиц по размерам d , найденными с помощью электронной микроскопии [4]. Эти функции уменьшаются с увеличением d при d > 9 нм, что соответствует результатам, полученным в настоящей работе, т. к. у наночастиц, имеющих магнитные моменты в исследуемом в ней диапазоне, расчетный размер магнитного ядра d > 12 нм. Исследование методом ЯМР функции распределения f ( P ) при меньших P и ее сравнение с измеренной методом электронной микроскопии функцией распределения f ( d ) позволит экспериментально оценивать граничное значение d , ниже которого частица становится немагнитной. Для исследования методом ЯМР функции распределения f ( P ) при Р < 4.5·10^–19 А·м² нужно увеличить напряженность намагничивающего поля Н н2 .