Исследование методом линейной регрессии зависимости механических характеристик керамических материалов от содержания кальцийсодержащего шлака черной металлургии

Кыштырлинское месторождение глины находится в Тюменской области и по суммарному содержанию А ₂ О ₃ + TiO ₂ относится к полукислым с высоким содержанием красящих оксидов ( Fe ₂ O ₃ более 3%). Согласно классификации глины по огнеупорности делят на три класса, исследуемая глина относится к - классу легкоплавких (огнеупорность 1220 - 1320^оС), по спекаемости к - неспекающимся, т.е. не способны при обжиге давать черепок без признаков пережога с водо-поглощением не более 5%.

Для изучения влияния шлака на физико-механические показатели кирпича были исследованы составы, приведенные в табл. 3.

Керамическая масса готовилась пластическим способом при влажности шихты 18-22%. Сформированный кирпич, высушенный до остаточной влажности не более 8%, обжигался при температуре 1050 оС.

При исследовании зависимости между содержанием шлака и основными механическими характеристиками кирпича использовался достаточно распространенный метод линейной регрессии. Этот метод позволяет выявить, как изменения одной переменной влияют на другую [12]. Модель строится на основании результатов фактического эксперимента и аналитически описывает зависимость результатов серии опытов.

При проведении экспериментов некоторые факторы, такие как давление прессования и температура обжига, не изменяли своих значений. Поэтому влияния на полученные результаты они не оказывали. Таким образом, определяющим фактором качества кирпича является единственный показатель — процентное содержание шлака в массе. Эксперимент состоял из 10 опытов. В первом опыте независимая переменная X принимала минимальное значение, равное 0%. В каж-

Таблица 1. Выбросы вредных веществ в атмосферу

Отрасль	Выбросы, %
Черная металлургия	24,3
Цветная металлургия	10,5
Энергетика	27,0
Автотранспорт	13,3
Нефтедобыча и нефтехимия	15,5
Промышленность строительных материалов	8,1

Таблица 2. Химический состав исследуемых компонентов

Компоненты	Содержание оксидов, мас. %
	SiO 2	Al 2 O 3 + TiO 2	Fe 2 O 3	CaO	MgO	R 2 O	SO 3	п.п.п.
Шлак от выплавки ферросплавов (г. Серов)	34,24	9,4	0,48	45,18	8,87	0,98	-	-
Кыштырлинская глина	55,38	19,46	7,52	1,75	1,82	2,73	1,82	8,42

Рис. 1. Рентгенограмма металлургического шлака

Таблица 3. Составы керамических масс

Компоненты Содержание компонентов (мас. %) 1 2 3 4 5 6 7 8 9 10 Кыштырлинская глина 100 90 85 80 75 70 68 65 62 60 Кальцийсодержащий шлак от выплавки ферросплавов - 10 15 20 25 30 32 35 38 40 дом последующем опыте содержание шлака уве- телей от содержания шлака имеют явно нелиней-

личивали, а в последнем опыте X приняла максимальное значение равное 40% (табл. 3). Зависимость механических показателей кирпича от содержания шлака представлена в табл. 4.Графики зависимостей функций Y ₁ , Y _2, Y _3, Y ₄ от Х (содержание шлака) имеют вид представленный на рис. 2.

Из рис. 2 видно, что все зависимости показа- ный характер.

Постановка задач заключалась в подборе функции – модели, описывающей экспериментальные данные, определения ее параметров, оценка точности и построение доверительных интервалов для данной функции. Отметим, что все исследуемые зависимости Y ₁ , Y _2, Y _3, Y ₄ имеют

Таблица 4. Экспериментальные данные зависимостей параметров изделия от содержания шлака

Показатели		Составы
		1	2	3	4	5	6	7	8	9	10
Х – содержание шлака	в %	-	10	15	20	25	30	32	35	38	40
	в долях	0,00	0,10	0,15	0,20	0,25	0,30	0,32	0,35	0,38	0,40
Y 1 – водопоглощение, %		11,2	11,2	11,2	11,1	11,0	10,8	11,3	12,0	13,2	15,0
Y 2 – прочность на сжатие, МПа		12,7	12,7	12,7	12,9	13,1	13,3	12,9	12,0	10,7	9,2
Y 3 – усадка, %		6,5	6,5	6,5	6,6	6,7	6,9	6,7	6,0	5,5	4,4
Y 4 – морозостойкость, циклы		28	28	28	29	30	32	29	26	20	14

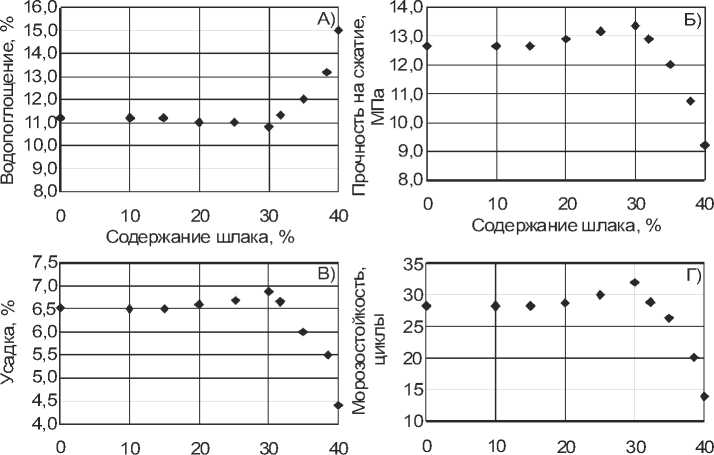
Содержание шлака, %

Содержание шлака, %

Рис. 2. Вид экспериментальных зависимостей показателей от содержания шлака: А) – водопоглощение; Б) – прочность на сжатие; В) – усадка; Г) – морозостойкость

качественно подобный характер, поэтому для данных зависимостей воспользуемся одной и той же моделью

Х 1 ( X ) =

a + cX + eX2 1 + bX + dX2

доверительными интервалами.

Для построения доверительного интервала по уравнению регрессии y = y ( x ) использовались следующие данные:

1. Оценка остаточной дисперсии по формуле (2)

которая как было показано в работах [1, 2, 3] является оптимальной. Затем для каждой из зависимостей Y ₁ , Y _2, Y _3, Y ₄ методом наименьших квадратов, найден коэффициент R ², а также были вычислены и построены 95% доверительные интервалы.

Значения параметров представлены в табл. 5, а на рис. 3 представлены модельные функции с

S

n

S (Ух -yj 2 _ i=1 i_________

n - 2

;

2. Средние значения независимой переменной по формуле (3)

Таблица 5. Значения параметров функций Y ₁ , Y _2, Y _3, Y ₄ и коэффициент R²

	Y 1 (Х)	Y 1 (Х)	Y 1 (Х)	Y 1 (Х)
a	11,30522	12,54797	6,39884	27,23876
b	-0,04563	-0,04833	-0,04592	-0,04935
c	-0,52691	-0,59187	-0,28393	-1,27577
d	0,00053	0,00060	0,00054	0,00063
e	0,00637	0,00714	0,00320	0,01516
R2	0,991	0,990	0,972	0,981

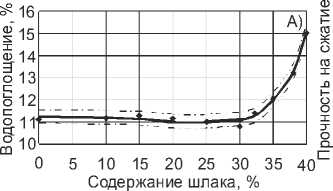
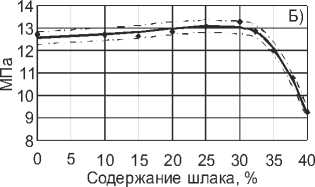
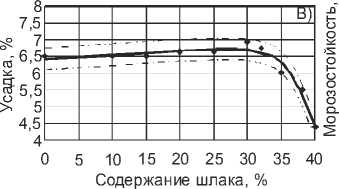
Рис. 3. Графики зависимостей водопоглощения, прочности на сжатие, усадки и морозостойкости от содержания шлака: А) – водопоглощение; Б) – прочность на сжатие; В) – усадка; Г) – морозостойкость. – модельная функция; 95% доверительные интервалы;

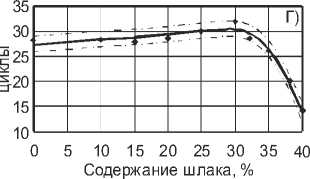
– экспериментальные данные

1n

X = Ё X ; n i=1 i

3. Оценка средней групповой дисперсии по формуле (4)

S

2 y _x

= s2

1+ n

(1 -x)2

Ё (1 - x )2

i = 1 i J

При определении доверительного интервала для индивидуальных значений зависимой переменной в пункте 3 можно использовать формулу (5)

S

2 y ₀

= s ²

1 + ¹ + n

к

⁽ x о ^- x ⁾²

n

Ё ( X i - x )² i = 1                 J

здесь х – значение переменной, для которой ищутся границы доверительного интервала.

Зная надежность gamma и число степеней свободы ( k = n – 2), по таблице Стьюдента находим t_{g , k} .

• 4.    Вычисляем отклонение: A = S • t„ , .

• 5.    Записываем результат в виде: y = y x ± A , с надежностью gamma.

yx     y , k

x – объясняющая переменная; y – фактические значения зависимой переменной; y_x – значение за в исимой переменной по уравнению регрессии; x – среднее значение x ; S ² – оценка остаточной дисперсии; n – число фактических данных; gamma – надежность.

Таким образом, экспериментальные данные показали, что кирпич имеет оптимальные физико–механические показатели при содержании

шлака в составах керамических масс 30%. Метод регрессионного анализа по результатам зависимостей физико – механических показателей от содержания количества шлака показал, что экспериментальные данные достаточно хорошо описываются математическими зависимостями с точностью, принятой в практических расчетах, приведенные модули дают достаточно хорошие результаты, поэтому их можно оставить в приведенном здесь виде.