Исследование методов моделирования цифровых автономных компенсаторов и систем регулирования

качество регулирования. Перекрестные каналы,

Повышение эффективности современного производства: улучшение качества выпускаемой продукции, минимизация производственных издержек, увеличение рентабельности и т. д. напрямую связано с необходимостью контроля и регулирования значительного числа технологических параметров (десятков, сотен, а иногда тысяч параметров). На многих высокотехнологических производствах для решения данных задач используются одноконтурные системы автоматического регулирования (САР), составляющие основу автоматизированных систем управления технологическими процессами (АСУТП) предприятия.

Однако наличие взаимного влияния управляющих воздействий на две и более управляемые величины (многосвязность объекта управления), контролируемых возмущающих воздействий, изменение статических и динамических характеристик технологического оборудования (процесса), вызванные изменением режима работы оборудования, характеристик сырья и теплоносителей, значительно снижают качество работы одноконтурных САР.

Взаимосвязь регулируемых величин характеризуется наличием в объекте основных и перекрестных каналов управления. Основные каналы, определяющие взаимосвязь технологического параметра с соответствующим регулирующим воздействием, обеспечивают желаемое заданное определяющие взаимосвязь технологических параметров с другими регулирующими воздействиями, приводят к нежелательному отклонению параметра от заданного значения (появлению ошибки регулирования), выступая в качестве дополнительных возмущающих воздействий. Это определяет сложность регулирования многосвязных объектов и необходимость устранения влияния перекрестных каналов.

Использование цифровых связанных систем регулирования (ЦССР), характеризующихся наличием внешних компенсирующих связей (компенсаторов) между регуляторами, обеспечивает частичную или полную автономность регулируемых параметров, позволяет повысить качество регулирования и придать системе определенные желаемые свойства [1]. Существующие способы расчета и моделирования ЦССР связаны со значительной сложностью и требуют выполнения значительных объемов аналитических преобразований [2]. Теоретической основой одного из способов является принцип автономности, позволяющий обеспечить независимое друг от друга регулирование связанных параметров [3].

Постановка задачи

Рассмотрим r -мерную цифровую систему управления (ЦСУ) (рисунок 1).

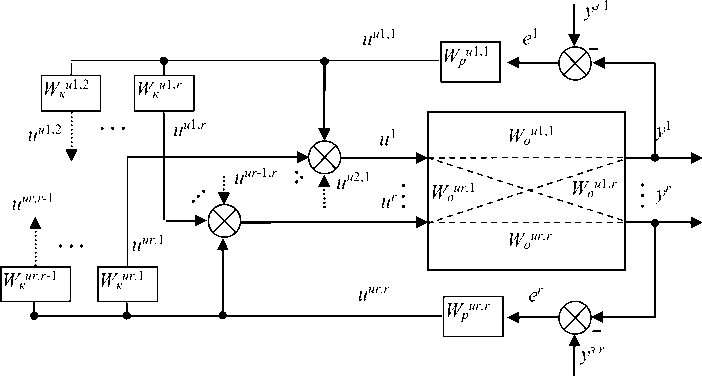
Рисунок 1. Структурная схема r -мерной системы управления

Figure1. Block diagram of the r -dimensional management system

В векторно-матричной форме система уравнений, описывающая её поведение, имеет вид:е =yз-y, uu =Wрu·е, u =Wкu·uu, y =Wоu·u, где е =[е1(z)…,еr(z)]Т –вектор ошибок управления; yз =[yз1(z)…,yз r(z)]Т –вектор заданий; y =[y1(z)…,yr(z)]Т –вектор выходов объекта управления (ОУ); иu =[иu1,1(z)…,иu r,r(z)]Т –вектор выходов регуляторов; и =[и1(z)…,и r(z)]Т –вектор управляющих воздействий; Wоu –матрица дискретных передаточных функций объекта по основным и перекрестным каналам, r х r; Wpu, Wk -диагональная матрица дискретных передаточных функций регуляторов и матрица дискретных передаточных функций компенсаторов, r х r; z -оператор временного сдвига; r -количество входов и выходов (размерность) системы.

Расчет дискретных передаточных функций (ПФ) автономных компенсаторов осуществляется по выражению [1]:

W к

uавт

_ ^pp иавт^ -1 , ppr ииавт

W o^u

W p^u

W k^u

W 0 ^1-1 ( z ) ... w o r ^-1 ( z ) w p ^1-2 ( z )... w p ; -² ( z )

W 1 r (z)... W r - r (z) w; u( z)...о "

о      ...о о     ... w;r • r (z)

1     ... w k ^{r J}( z )

w k    z )... w p r _ -² ( z )

wk 1 r (z)...1

где W o^uaem - блочная матрица, элементами которой являются матрицы дискретных передаточных функций основных и перекрестных каналов объекта, ( r • ( r - 1)) х ( r • ( r - 1)) ; w ku^a^^m - блочный вектор, элементами которого являются векторы дискретных передаточных функций компенсаторов, r • (r-1); W o^uuaem - блочный вектор, элементами которого являются векторы дискретных передаточных функций перекрестных каналов объекта, r • (r-1).

Поскольку расчет автономных компенсаторов основан на обращении и перемножении матриц (1), то их ПФ имеют вид дробно-рациональных выражений, числитель и знаменатель которых представляются как сумма ( r • ( r - 1))!

p i-j k _o

E l P i - j    - h +1

bh    ‘ z         ua“j где  Woui -j( z ) = -h^--z-1-d0    -дис- no

1 - Z a -j z ^{- h} h =1

кретная передаточная функция объекта по основным (i =j) и перекрестным (i j каналам ;

слагаемых, каждое из которых является произведением (r • (r-1)) ПФ каналов объекта:

W k

i ’^{j ( z} ) =

( r ■ ( r - 1))!

Z

Ц = 1

П W O ^rfV'^ ( z )

Z П w:

ц' = 1    V   v' = 1

u j ^j k _рк

Z q     ■ z - ^h

Wyj (z) = —h=°—-------- -дискретная пере- nрк

1 - Z p P ^j z ^{- h} h =1

даточная    функция j-го    регулятора;

где W P ^{ak v ,e}^ ^v ( z ) , W P ^x ^ ^{,v ,Y} ^, ^V ( z ) -ПФ каналов объ

екта; а^ц,\ e ^ ^,v, ^'^,v, Y ^' ^,V = 1 - r -индексы, принима-

u i’j kрк

V Лu i-j  -hh - d pk

Z q h ^z

WPi-j( z) =       ----------- nрк

1 -Z pPJ z- h h=1

–дискретная пере-

даточная функция компенсатора перекрестной

связи (i ^j); a^u i ^{- j} , b^p i ^{- j} ' , d— i’j -параметры

и число тактов запаздывания дискретной передаточной функции канала объекта; k — i ^{- j} , n — i ^- j –порядки числителя и знаменателя дискретной передаточной функции основного (i =j) или перекрестного (i j канала объекта; q ^p i ^{- j} , p ^u i ’ j ,

ющие натуральные значения из диапазона 1 r ; p, v -номер слагаемого и номер сомножителя в числителе (2); р', v' -номер слагаемого и номер сомножителя в знаменателе (2).

Для упрощения описания дальнейших преобразований и выводов введем новые обозначения:

W0 -a' VH"v (z) = WH,v (z), W“ ^'^ (z) = W^' (z), (r • (r-1))! = M , (r • (r -1)) = N, где Wц,¥ (z), Wц>' (z) -ПФ каналов объекта;

d ui^j -параметры и число тактов запаздывания дискретной передаточной функции регулятора (i =j) или компенсатора (i ^j); k u^j , n ^p ij -порядки числителя и знаменателя дискретной передаточной функции регулятора (i =j) или ком

пенсатора (i ^j); i, j = 1 - r .

р-р = 1-M ; v-v′ = 1-N.

В процессе синтеза системы расчет численного значения выходов всех элементов осуществляется на основе конечно-разностных уравнений. Для получения конечно-разностного уравнения автономного компенсатора необходимо его ПФ, представленную формулой (2), привести к одноэтажному дробно-рациональному выражению относительно оператора сдвига z, что требует выполнения большого объема аналитических преобразований.

В работе [2] приводится алгоритм, обеспечивающий автоматическое выполнение аналитических преобразований, реализуемый на ЭВМ. Однако использование данного алгоритма автоматизированного выполнения преобразований не обеспечивает получения искомого результата в силу недостатка самой методики. Суть недостатка заключается в недопустимости округления результата перемножения дробных чисел при вычисления коэффициентов ПФ компенсаторов, что нереализуемого в силу ограниченности разрядной сетки ЭВМ. В конечном счете, для систем размерности больше двух это приводит к не реализуемости условия автономности и неработоспособности системы.

В связи с этим поставлена задача разработки алгоритма, обеспечивающего высокую точность расчета численного значения выхода автономного компенсатора r-мерной ЦСУ по известной ПФ (2) в автоматическом режиме.

Разработка метода расчета

В данной работе предлагается метод, базирующийся на представлении автономного компенсатора в виде последовательно-параллельного соединения элементов с ПФ основных и перекрестных каналов объекта управления в соответствии с правилами структурного преобразования. Из выражения (2) следует, что автономный компенсатор можно представить в виде последовательного соединения элементов.

u

W' ( z )

θ --------►

1/ W'' ( z )

y

Рисунок 2. Схема автономного компенсатора: u – вход компенсатора; θ – выход звена с ПФ W' ( z ); y – выход компенсатора

Figure 2. Autonomous driving compensator: u – the input of the compensator; θ – the output level with PF W '(z); y– the output of the compensator

M N

W'(z) = ЯП W (z )|

Ц=1 V V=1

W"(z) =ffn W Ц'У (z) I н'=1 V v'=1

Выход автономного компенсатора можно найти путем последовательного расчета численных значений выходов элементов с ПФ W '( z ) и 1/ W "( z) .

В свою очередь W '( z ) (3) на основании правил структурного преобразования, представляет собой M цепочек, каждая из которых состоит из N элементов с ПФ моделей каналов объекта (рисунок 3).

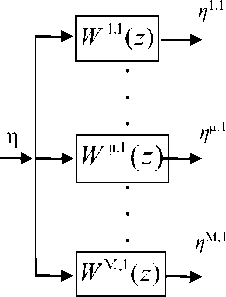
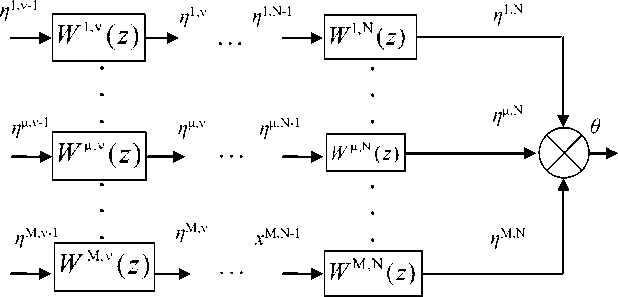
Рисунок 3. Схема соединения элементов, входящих в W ( z )

Figure 3. Connecting diagram elements included in W ( z )

В общем случае система конечно-разностных уравнений, используемая для описания элементов последовательно-параллельного соединения (рисунок 3), примет вид:

n

Ц.1 _ V z^-1

п =Laj j=1

k ^{Ц -1}

+ L b> 4-j - d -1 .

n ^’V

P,v X ' _U,V    U,V . X ' m,V U,V- ni =Laj  -^i-j+Lbj  -ni-j-d-V, j=1

M

9i =Lnj-N ,(7)

j = 1

где n ^^,v —выход v-го элемента ц-й цепочки; a ^ ’ ^V , b ^’ ^V , d ^{R , V} -параметры и целое число тактов запаздывания моделей каналов объекта; k ^ ^{, V} , n ^ ^{, V} -порядки правой и левой частей моделей каналов объекта; р ^^,1 -выход 1-го элемента ц-ой цепочки.

Вестник ВГУИТ/Proceedings of VSUET, № 4, 2016

По уравнению (5) рассчитывается выход

1-го элемента, а по (6) -v-го элемента (v = 2,N) в μ-ой цепочке. Выход всего последовательнопараллельного соединения f (элемента с ПФ W '( z )) рассчитывается по выражению (7).

Система уравнений (5) –(7) позволяет найти выход звена с ПФ W '( z ) (рисунок 2), без выполнения сложных аналитических преобразований, поскольку использует заранее известные модели каналов объекта.

Сложность расчета выхода второго элемента (рисунок 2) связана с дробно-рациональным видом его ПФ, в знаменатель которой входит сумма произведений ПФ каналов ОУ. Для решения данной задачи предложено два метода.

В соответствии с первым методом предлагается рассмотреть выход y в качестве входа, а вход f в качестве выхода.

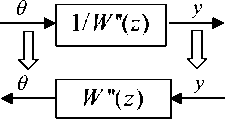
Рисунок 4. Схема расчета выхода звена с ПФ 1/ W "( z )

• Figure4. The scheme of calculating the output level with PF 1/ W "( z )

Данный прием позволяет избавиться от дробно-рационального вида ПФ второго элемента (рисунок 2) и представить взаимосвязь сигналов f и y, как и в предыдущем случае, в виде последовательно-параллельного соединения элементов с ПФ каналов объекта, где известен выход f и требуется найти вход y (рисунок 5).

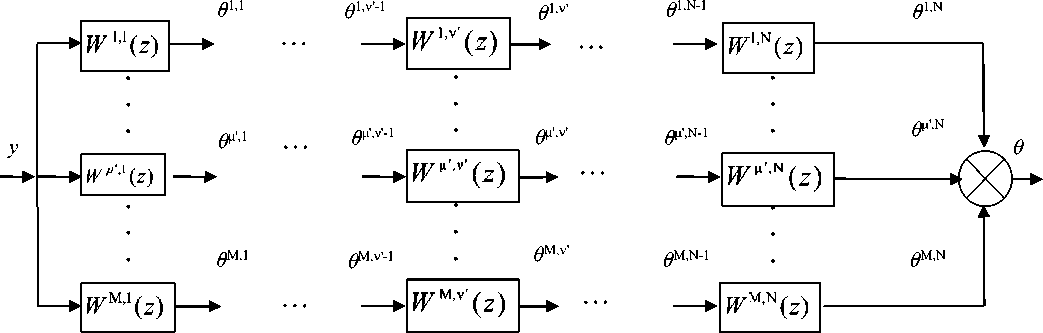
Рисунок 5. Схема соединения элементов, входящих в выражение W "( z )

Figure 5. Connecting diagram elements contained in the expression W "( z ) .

Система уравнений, описывающая взаимосвязь сигналов θ и y примет вид:

для расчета 1-го элемента в µ '-ой цепочке:

• n W            k W

• O^'1 = Yaf -0/'' +У bf - y(8)

• i               j        i ^- j          j        i - j - d ^gJ

j=1

для расчета v '-го (v' = 2, N) элемента в ц '-ой цепочке:

n ^f'^v

0f'v = Ya^’v -0^'^+Yb^’v - 0       .(9)

i       Z—l j       i—j Z—l j       i - j - d *-v j=1

Выход соединения определяется по формуле:

Μ

0i=£0f^ .(10)

ц' = 1

В общем случае любой канал объекта может иметь транспортное запаздывание. Поэтому представим каждый элемент цепочки в виде последовательного соединения звена без запаздывания и звена чистого запаздывания (рисунок 6).

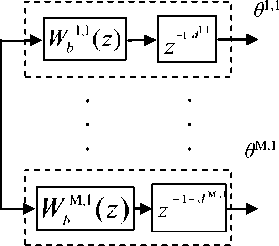
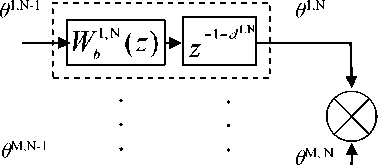
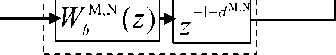
Рисунок 6. Представление ПФ W "( z ) в виде соединения звеньев без запаздывания и звеньев чистого запаздывания. W b ( z ) - ПФ канала без запаздывания

θ

—►

Figure 6. Presentation of PF W "( z ) as a compound units without delay and units of pure delay. W_b ( z ) - PF channel without delay

Преобразуем схему с учетом суммарного запаздывания каждой цепочки (рисунок 7).

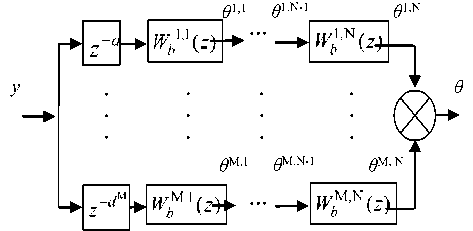
Рисунок 7. Представление ПФ W "( z ) в виде соединения звеньев без запаздывания и звеньев суммарного чистого запаздывания

Figure 7. Presentation of PF W "( z ) as a compound units without delay, and the delay units of the total net

При этом z d -передаточная функция звена чистого запаздывания μ'-й цепочки, а d*’=£(1 + d^'v‘).

Определяя минимальное из суммарных запаздываний всех цепочек, преобразуем схему к виду(рисунок 8).

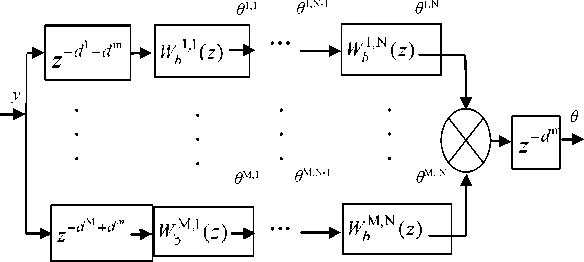
Рисунок 8. Преобразованная структурная схема

Figure8. The transformed structural diagram

При этом d ^m =min( d ^ц ) -минимальное из запаздываний цепочек последовательнопараллельного соединения (рисунок 7). В результате получим цепочки с запаздыванием и без запаздывания.

На основании структурной схемы (рисунок 8) по известным значениям сигнала y осуществляется последовательный расчет выходов элементов цепочек 0 "^Л' с запаздыванием (8) -(9). Из уравнения (10) вычисляется суммарный выход цепочек без запаздывания:

р

У 0 c ^- ■    0 i — у 0 s • ,          (ii)

c = 1                     s = 1

где ρ –количество цепочек без запаздывания (ρ ≤r); l –количество цепочек с запаздыванием (l

Для цепочек без запаздывания уравнение (9) для последнего элемента можно записать в виде:

n

k

0 s ^{- N} = У a f ^N -0 s —N + y b t ^{- N} -0 / . + b s ^{- N} -0 T ^{N- 1 (12)} t = 1                      t = 2

В свою очередь уравнение для предпоследнего элемента (с номером Ν-1) имеет вид:

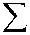
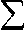
n s - ^{N- 1}                               k s ’ ”— ¹

0 s-N—1 = as-N—1 -0 s-N 1 + b-N—1 -0 s-N"2 + i                         t              I — t                     t              I — t + 1

t =2                      ⁽¹³⁾

+ b s ^{N- 1} -0 ^s - ^{N— 2}

Вместо 0 s ’ ^{N 1} выражения (12) подставим правую часть выражения (13):

n s - ^N                    k - ^N

Д s- N _ V   s -N A s -N , V"¹ i s -N A s - N—1 ,

0 i  = У at  -0 i—t + У bt  -0 i—t+1 + t=1

n ^{s N 1}                                   k ^s - ^{N 1}

+bs-N - ( У asN—1 - 0s-N 1 + У bs-N—1 - 0siN—2

t=1

+bs’N—1 -0s-N—2

После преобразований получим:

n

0 s - ^N =y a ^sN it

k^s - ^N

0 s - N + У УN i —tt t =2

Qs - N— 1  ,

^-0 i — t + 1 ⁺

n ’ b 1 s - ^N - у a .

s N— 1 s N— 1 ' t        ^{- 0} i — t

k- - ^{N— 1}

+ b s- ^N - У b^ ^—

1t t=2

Л s - N— 2  ,

^-0 i — t + 1   ⁺

+ b s ^N - b ^{s N— 1} -0 s ^{- N— 2}

Выполняя аналогичные действия для всех остальных элементов цепочки, приходим к выражению, связывающему вход y и выход s-ой цепочки 0 s ’ ^N :

0 s

j =N ^^ t = 1

+ E b t + 1 -0 sj ^{— 1} t = 0

j + 1

- П b .’ q =N

. I

n^s -

+ у

k^{s 1}

a s ^-1 -0 s ’1 + Tb s ¹ -0 s ’ t         I — t              t         I — t + 1

t = 2

2                  1

л b s ^{- q} + П b s^q - y i

=N       q =N

Подставляя в (11) вместо 0 s ^{- N} правую часть (15) получим выражение для расчета значения входа на текущем такте:

( р                 р  (   2 II  nc’j                         kc’j                       I   j+1          I y =I yeN —zl Zl I уacJ -0ct +УbcJ-6ct-1 I-ПbC- 1+(16)

V. c = 1              c = 1 I j =N I I   t = 1                       t = 1                    J   q =N         J '      ^

C - ¹                                                     C - ¹

/ n                           k ’

+l у a t ^-1 - о с -1 + y b t ^-1 -o ^C: 1 _{+ 1}

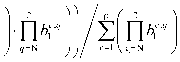
р где bt-N+1 = 1; У0С-N - сумма выходов цепочек с=1

без запаздываний.

Найденная величина является искомым выходом звена с ПФ1/ W "( z ) и автономного компенсатора в целом.

Из выражения (16) следует, что при расчете выхода автономного компенсатора на текущем такте квантования используются значения выходов элементов цепочек без запаздываний на предыдущих тактах. Поэтому для расчета численного значения выхода автономного компенсатора на каждом последующем такте квантования необходимо рассчитать выходы элементов цепочек без запаздываний по выражениям (8)–(9) на текущем такте.

Таким образом, итерационный алгоритм поиска численного значения выхода автономного компенсатора на основании предложенного метода включает выполнение следующих этапов:

• 1.    По выражениям (5) – (6) рассчитывается значение выхода объекта с ПФ W '( z );

• 2.    Определяется минимальное суммарное запаздывание из всех слагаемых, входящих в W "( z ) (4);

• 3.    По выражениям (8) – (9), (11) рассчитывается суммарный выход цепочек без запаздывания для элемента с ПФ W "( z );

• 4.    По (16) вычисляется величина входа элемента с ПФ W "( z ) (выхода элемента с ПФ 1 / W "( z )) на текущем такте;

• 5.    По выражениям (8) – (9) рассчитываются выходы промежуточных звеньев цепочек без запаздываний, необходимые для расчетов на последующих тактах.

Среди недостатков данного метода можно указать относительную громоздкость используемых математических выражений и сложность алгоритма расчета.

В связи с этим предложен второй метод расчета выхода второго элемента (рисунок 2) с дробно-рациональным видом ПФ, в знаменатель которой входит сумма произведений ПФ каналов ОУ. его суть заключается в рассмотрении обратных сигналов входа и выхода, т. е. 1/ f и 1/ y . Данный переход позволяет перейти от передаточной функции 1/ W "( z ) к передаточной функции W "( z ) (рисунок 11).

Рисунок 9. Способ расчета выхода звена с ПФ 1/ W'' ( z ) на основе обратных величин

Figure 9. A method of calculating the output level from the PD 1 / W '' (z) based on the reciprocals

После этого моделирование элемента осуществляется тем же способом, что и звена с ПФ W '( z ). Для этого используются зависимости аналогичные выражениям (5)–(7). Недостатком данного подхода является невозможность формирования на входе элемента бесконечно большого значения, в случае когда сигнал f равен нулю. Это приводит к появлению некоторой погрешности, величина которой от одной итерации расчета к другой будет расти, что в итоге может привести к существенному искажению конечного результата и как следствие к неработоспособности системы.

Проверка достоверности и работоспособности разработанных методов моделирования автономных цифровых систем регулирования осуществлялась путем численного моделирования четырехмерной системы регулирования.

В качестве объекта управления выбран технологический процесс синтеза аммиака, протекающий в 4-x слойном полочном реакторе в присутствии катализатора с промежуточным охлаждением между слоями (рисунок 9). Структура взаимосвязи каналов объекта представлена на рисунке 10. Значения параметров моделей основных и перекрестных каналов приведены в таблице 1.

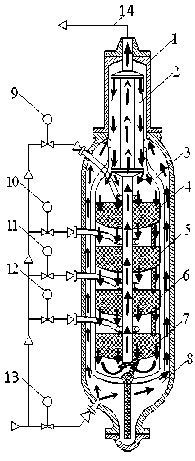
Рисунок 10. Реактор синтеза аммиака мощностью 1360 т/сут: 1 – корпус колонны; 2 – внутренний теплообменник; 3 – корпус катализаторной коробки; 4, 5, 6, 7 – I, II, III, IV катализаторные слои соответственно; 8 – пространство между корпусом колонны и катализаторной коробки; 9, 10, 11, 12 – клапаны подачи холодного газа на полки колонны; 13 – основной клапан подачи смеси по основному ходу колонны; 14 – выход колонны (смесь газообразного аммиака, водорода и азота)

Figure 10. Ammonia synthesis reactor capacity of 1360 t / day: 1 – the case of the column; 2 – internal heat; 3 – the case of the catalyst of the box; 4, 5, 6, 7 – I, II, III, IV catalyst layers, respectively; 8 – the space between the casing column and rolled-mash of the box; 9, 10, 11, 12 – cold gas flow valves to column flange; 13 – main control valve supplying the mixture in the main course of the column; 14 – output of the column (a mixture of gaseous ammonia, hydrogen and nitrogen)

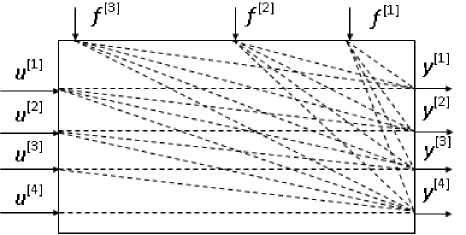
Рисунок11. Структурная схема взаимосвязи парамет-ров: u ^[1] ÷ u ^[4] – степени открытия заслонок на байпасных потоках (управляющие параметры); y ^[1] ÷ y ^[4] – температура в слоях катализатора (управляемые параметры); f ^[1], f ^[2], f ^[3] ÷ концентрация аммиака, инертных газов и соотношение водород/азот (возмущающие воздействия)

Figure 11. Block diagram of the relationship of parameters: u ^[1] ÷ u ^[4] - the degree of opening of valves in the bypass flow (control parameters); y ^[1] ÷ y ^[4] – The temperature in the catalyst layers (controlled parameters); f ^[1], f ^[2], f ^[3] ÷ concentration of ammonia, inert gases and the hydrogen / nitrogen (disturbance variables)

Таблица 1.

Параметры дискретной четырехмерной полной модели ОУ процесса синтеза аммиака

Table 1.

The parameters of a discrete model of the four full OU ammonia synthesis process

Канал Channal	a 1	a 2	b , %/ ºС	d, такт tact
Степень открытия первой заслонки –температура в первом слое катализатора. The first valve opening degree - the temperature in the first catalyst layer ( W оu [1][1] )	1,206811	-0,244581	0,64043	10
Степень открытия второй заслонки –температура во втором слое катализатора. The second valve opening degree - the temperature in the second catalyst layer ( W оu [2][2] )	1,250636	-0,28338	0,262926	16
Степень открытия третьей заслонки –температура в третьем слое катализатора. The third valve opening degree - the temperature in the third catalyst layer ( W оu [3][3] )	0,977349	-0,012609	0,213039	24
Степень открытия четвертой заслонки –температура в четвертом слое катализатора. The fourth valve opening degree - the temperature in the fourth catalyst layer ( W оu [4][4] )	1,020477	-0,045886	0,102611	30
Степень открытия первой заслонки –температура во втором слое катализатора. The first valve opening degree - the temperature in the second catalyst layer ( W оu [1][2] )	1,079484	-0,106821	0,082372	18
Степень открытия первой заслонки –температура в третьем слое катализатора. The first valve opening degree - the temperature in the third catalyst layer ( W оu [1][3] )	1,120682	-0,145529	0,037712	28
Степень открытия первой заслонки –температура в четвертом слое катализатора. The first valve opening degree - the temperature in the fourth catalyst layer ( W оu [1][4] )	0,755068	0,215573	0,014607	34
Степень открытия второй заслонки –температура в первом слое катализатора. The second valve opening degree - the temperature in the first catalyst layer ( W оu [2][1] )	1,063117	0,095382	0,089176	19
Степень открытия второй заслонки –температура в третьем слое катализатора. The second valve opening degree - the temperature in the third catalyst layer ( W оu [2][3] )	0,897605	0,078798	0,023784	38
Степень открытия второй заслонки –температура в четвертом слое катализатора. The second valve opening degree - the temperature in the fourth catalyst layer ( W оu [2][4] )	1,004704	-0,027202	0,009057	46
Степень открытия третьей заслонки –температура в первом слое катализатора. The third valve opening degree - the temperature in the first catalyst layer ( W оu [3][1] )	1,09690	-0,126882	0,041269	29
Степень открытия третьей заслонки –температура во втором слое катализатора. The third valve opening degree - the temperature in the second catalyst layer ( W оu [3][2] )	1,014329	0,039309	0,022401	39
Степень открытия третьей заслонки –температура в четвертом слое катализатора. The third valve opening degree - the temperature in the fourth catalyst layer ( W оu [3][4] )	0,950717	0,025159	0,004863	50
Степень открытия четвертой заслонки –температура в первом слое катализатора The fourth valve opening degree - the temperature in the first catalyst layer. ( W оu [4][1] )	0,939813	0,033397	0,012603	35
Степень открытия четвертой заслонки –температура во втором слое катализатора. The fourth valve opening degree - the temperature in the second catalyst layer ( W оu [4][2] )	1,102983	-0,126918	0,008534	47
Степень открытия четвертой заслонки –температура в третьем слое катализатора. The fourth valve opening degree - the temperature in the third catalyst layer ( W оu [4][3] )	1,012685	-0,040337	0,004862	52

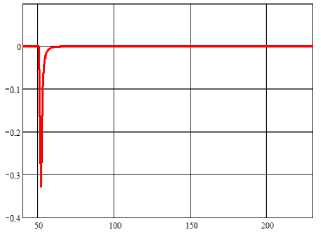
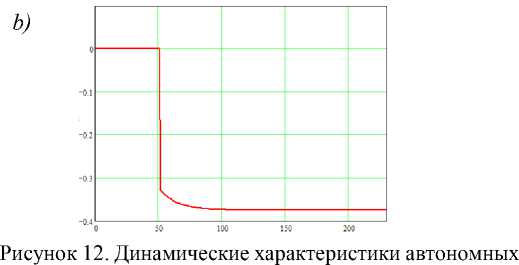
компенсаторов а) рассчитанные при обращении сигна лов; б) рассчитанные при инвертировании направления сигналов (предложенная методика)

Figure 12. The dynamic characteristics of autonomous expansion joints a) designed for handling signals; b) calculated by inverting the direction of the signal (the proposed method)

На первом этапе осуществлялось моделирование одного из автономных компенсаторов, связывающего выходы первого и второго регуляторов. Результаты моделирования по первому и второму предложенному методу, представленные графиками переходных процессов (рисунок 12), сравнивались с эталонным, полученным на основе аналитического расчета передаточной функции компенсатора в явном виде.

Анализ результатов показывает, что использование первой предложенной методики позволяет получить переходной процесс, полностью совпадающий с эталонным (рисунок 12 б ). Динамическая характеристика, полученная на основе обращения сигналов (рисунок 12 а ) вначале имеет схожий характер, однако затем сходится к прежнему установившемуся значению, что существенно отличается от эталонной. Это подтверждает предположение о влиянии невозможности цифровой вычислительной техники оперировать с бесконечно малыми и бесконечно большими величинами.

На втором этапе моделировалась работа всей четырехмерной цифровой автономной системы регулирования. В первом случае работа всех автономных компенсаторов моделировалась на основе первого метода, кроме компенсатора 12, работа которого моделировалась согласно второму методу. Во втором случае работа всех компенсаторов моделировалась по первому методу.

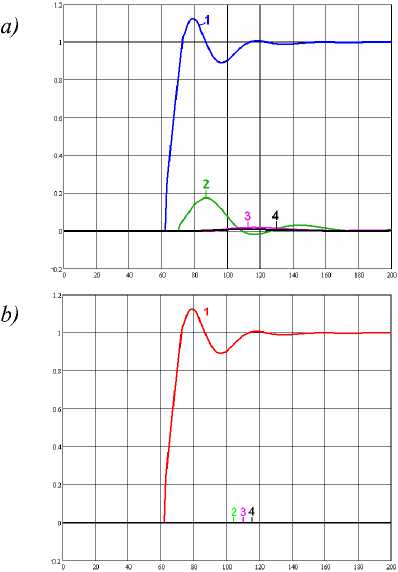
Рисунок 13. Динамические характеристики процесса синтеза аммиака (по заданию только на первый канал) а) рассчитанные при обращении сигналов; b) рассчитанные при инвертировании направления сигналов; 1, 2, 3, 4 – температура катализатора в соответствующих слоях

Figure 13. The dynamic characteristics of the ammonia synthesis process (only on the instructions of the first channel) a) designed for handling signals; b) calculated by inverting the direction of the signal; 1, 2, 3, 4 – the catalyst temperature in the respective layers

Как видно из графиков (рисунок 13), использование первого метода даже для расчета одного из компенсаторов не позволяет полностью устранить влияние перекрестных связей на температуру во втором, третьем и четвертом слоях катализатора. Применение же второго способа реализует принцип автономности в полном объеме.

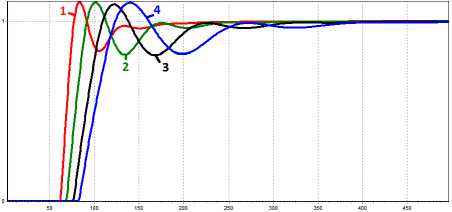
Рисунок14. Динамические характеристики процесса синтеза аммиака при изменении заданий по температурам на всех слоях катализатора; 1, 2, 3, 4 – температура в каждом слое.

Figure 14. The dynamic characteristics of processes sa ammonia synthesis when changing tasks at all temperatures of the catalyst layers; 1, 2, 3, 4 in each layer temperature

Заключение

Несмотря на указанные ранее относительные недостатки, результаты моделирования подтвердили достоверность и работоспособность первого предложенного метода моделирования и реализации автономных компенсаторов и системы в целом. Второй же подход, несмотря на простоту и легкость использования приводит к получению недостоверных результатов и в конечном счете к невозможности реализации автономной системы регулирования.