Исследование методов выбора оптимального маршрута движения по пересеченной местности при доставке спасателей к месту чрезвычайной ситуации

Сегодня задачи поиска оптимального пути от одной точки до другой возникают во многих прикладных областях. От гражданских и мирных, таких как проектирование маршрутов движения общественного транспорта, до военных и стратегических задач — передислокация войск и пути наступления. Не обходит стороной и область чрезвычайных ситуаций (ЧС). Её следует выделить отдельно, так как данная исследовательская работа проводилась в интересах Министерства по чрезвычайным ситуациям (МЧС) и посвящена поиску оптимального маршрута при реагировании на ЧС.

Важным в работе МЧС является скорость реакции и принятия необходимых мер для ликвидации ЧС, ведь от этого зависят не только количество человеческих жизней, а так же и состояние экологии окружающей среды. Доставка оборудования и спасателей на место ликвидации аварии оперативно и в кротчайшие сроки - неизбежный и актуальный вопрос в ходе реакции МЧС на происшествие, который опирается, в свою очередь, на выбор маршрута, по которому необходимо следовать до точки назначения.

Решение подобной задачи было бы нецелесообразным вне существующих направлений развития информационных технологий. Разработка подобного алгоритма и реализация его в виде программной компоненты имеет прикладное значение в области геоинформатики и геоинформационных систем (ГИС).

Географической информационной системой (ГИС) называется аппаратно-программный человеко-машинный комплекс, обеспечивающий сбор, обработку, отображение и распространение пространственных данных, интеграцию данных, информации и знаний для их эффективного использования при решении научных и прикладных задач, связанных с инвентаризацией, анализом, моделированием, прогнозированием и управлением окружающей средой и территориальной организацией общества.

ГИС как системы проектируются, создаются и эксплуатируются в комплексе составляющих их компонентов (блоков, подсистем, функциональных модулей), обеспечивающих функциональную полноту, адекватную решаемым задачам, возможность расширения функций и модификации системы.[3]

В общем случае состав ГИС можно представить в виде следующих компонентов (рис. 1):

• 1)    Данные (пространственные данные):

• -    позиционные (географические): местоположение объекта на земной поверхности;

• -    непозиционные (атрибутивные): описательные;

• 2)    Аппаратное обеспечение (ЭВМ, сети, накопители, сканер, дигитайзеры и т. д.);

• 3)    Программное обеспечение (ПО), которое включает в себя

• -    подсистему ввода данных;

• -    подсистему хранения и редактирования;

• -    подсистему анализа;

• -    подсистему вывода;

• 4)    Технологии (методы, порядок действий и т. д.). [3]

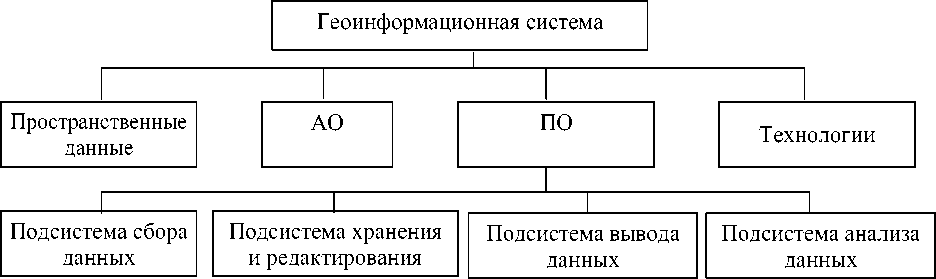
Рис. 1. Структура геоинформационной системы.

Таким образом, с технологической точки зрения поставленной задачей является разработка программного компонента подсистемы анализа данных для геоинформационной системы.

Несмотря на разброс областей применения, задача выбора маршрута сводится к теоретическим задачам поиска пути на графе. Направленный граф создается, принимая ячейки как вершины графа и возможные перемещения к соседним ячейкам как направленные грани между вершинами. Функция веса определена назначением стоимости к каждой грани, соответствуя «стоимости» перемещения по грани определенной при постановки задачи (время, длина, или любая функция, соответствующая данной проблеме). Для нахождения кратчайших путей в графах разработано и реализовано на различных языках программирования много различных алгоритмов. К ним можно отнести алгоритмы: Дейкстры, Дейкстры - Грибова, Левита, Йена, Флойда - Уоршелла, Форда-Беллмана, Джонсона. Поэтому разработчикам программного обеспечения в ходе решении конкретных прикладных задач приходиться использовать накопленный опыт лишь в качестве базовых рекомендаций, а создание программ требует проведения определенных исследований, как особенностей предметной области, так и характеристик используемой аппаратной составляющей, а в нашем случае и способности человека к преодолению различного рода препятствий.

Итак, отметим основные критерии выбора алгоритма поиска кратчайшего пути. Во-первых, путь должен быть оптимальным с точки зрения временных затрат. Следует сделать оговорку, что самый быстрый путь не является самым коротким. Скорее, вопрос поиска короткого пути -лишь частный случай поиска быстрого пути (то есть считается, что все шаги равномерны). Учитывая эти нюансы, сделаем вывод, что нам необходим алгоритм решения поиска быстрого пути. Во-вторых, наш путь должен быть наименее опасным как для автотранспорта, так и для человека. Наиболее частыми проблемами, с которыми сталкивается водитель на сложном рельефе, являются диагональное вывешивание и застревание из-за соскальзывания на препятствие или в него. Диагональное вывешивание означает, что два колеса по диагонали, как это следует из названия, теряют сцепление с поверхностью. Если эту неприятность еще можно предусмотреть, то предугадать падение днищем на камень или сползание мостом на перелом рельефа почти невозможно. Разбросанные на поверхности камни и валуны, канавы и бугры естественного или искусственного происхождения - довольно трудно проходимые участки пути на автомобиле. Тогда, для преодоления опасного рельефа следует выбрать либо пеший способ передвижения через данный участок (в том случае, если позволяют физиологические способности человека), либо выбрать обходной путь на автомобиле, который будет наиболее удобным и безопасным. Но следует помнить, что утомление, наступающее на дистанции под влиянием физической и умственной нагрузки, вызывает значительные изменения в организме человека. Особенно отчетливо эти признаки проявляются, как правило, на последней части дистанции. Появляется трудность в концентрации внимания и его распределении при чтении карты, а также в запоминании нужных ее элементов. Снижение работоспособности у человека накладывает и определенный отпечаток на выбор пути движения. Слабое восприятие, замедленная переработка полученной информации и ухудшенное ее запоминание вынуждают его выбирать более грубые, легко запоминающиеся ориентиры, избегать длинных, обходных, скоростных вариантов пути движения. Поэтому, на мой взгляд, будет правильнее следовать на автомобиле до того момента, пока вариант пересечения препятствия на автомобиле будет невозможным.

Исходя из всего вышесказанного, сделаем вывод, что при выборе алгоритма, нам необходимо учитывать его возможность заключать в себе некоторые функции, описывающие способности человека и автомобиля прохождения различных участков пути и, соответственно, саму характеристику рельефа.

Перейдем к рассмотрению алгоритмов. На данный момент общеизвестными являются следующие алгоритмы поиска пути: поиск в ширину; алгоритм “лучший-первый”; алгоритм поворота Креша; алгоритм «разделяй и властвуй»; алгоритм Дейкстры; алгоритм А*.[4]

В ходе их изучения выяснилось, что в нашем случае алгоритм поиска в ширину не является оптимальным по следующим причинам:

• 1)    поиск идет равномерно во всех направлениях, вместо того, чтобы быть направленным в сторону цели;

• 2)    не все шаги равны (по крайней мере, шаги по диагонали должны быть длиннее ортогональных);

• 3)    используя этот алгоритм, мы будем не в силах описать функции, заключающие в себе способности различных видов передвижения [3].

Алгоритм поворота Креша оценивает путь не весь сразу, а только на один шаг. Следовательно, алгоритм будет опускать все изменения на карте после начала движения. Переоценка маршрута после начала движения не является оптимальной. Более того, алгоритм поворота Креша не будет работать на пересеченной местности (но от ухода от деревьев/болот (мелких препятствий), возможно, он подойдет). Этим недостатком обладает так же алгоритм «разделяй и властвуй»[1].

Наиболее подходящим, на наш взгляд, является алгоритм Дейкстры. Е. Дейкстра разработал классический алгоритм для прохода по графам, грани которых имеют различный вес. На каждом шаге, он ищет необработанные узлы, близкие к стартовому, затем просматривает соседей найденного узла, и устанавливает или обновляет их соответствующие расстояния от старта. Этот алгоритм имеет два преимущества по сравнению с поиском в ширину: он принимает во внимание длину пути и обновляет узлы, если к ним найден лучший путь. Однако, он имеет слабость поиска в ширину, игнорируя направление к цели.[2]

Тогда, обратим внимание на следующий алгоритм - алгоритм «лучший - первый». Поиск «Лучший — первый» — это алгоритм поиска, который исследует граф путём расширения наиболее перспективных узлов, выбираемых в соответствии с указанным правилом.

Иудеи Перл (англ. Judea Pearl) описал поиск «Лучший — первый», взяв в качестве оценки узла значение некоторой «эвристической функции, которая, вообще говоря, может зависеть от описания цели, информации, собранной на данный момент и, самое главное, на каких-либо дополнительных знаниях о предметной области».[2]

Некоторые авторы использовали поиск «Лучший — первый» специально для описания поиска с эвристикой, чтобы попытаться предсказать, насколько близко находимся к финальному состоянию, так что пути, которые имеют лучшую эвристическую оценку, рассматриваются первыми. Этот специфический тип поиска называется жадным поиском «Лучший — первый».

Эффективный выбор текущего лучшего кандидата для расширения поиска, как правило, реализуется с помощью очереди с приоритетом.

Данный алгоритм так же имеет и свои слабости. Он не принимает во внимание накопленную стоимость пути, направляясь по прямой через зону с высокой стоимостью, а не обходя ее. [2]

Из всего вышесказанного сделаем вывод, что наиболее подходящими алгоритмами являются алгоритм Дейкстры и алгоритм «лучший-первый». Но преимущества одного алгоритма, являются недостатком другого и наоборот. Поэтому необходим алгоритм, сочетающий в себе учет длины предыдущего пути из алгоритма Дийкстры с эвристикой из алгоритма "лучший-первый". Тогда, интересным становится рассмотрение алгоритма А*. Ознакомимся с ним более детально.

Этот алгоритм был впервые описан в 1968 г. Питером Хартом, Нильсом Нильсоном и Бертрамом Рафаэлем. В их работе он упоминается как «алгоритм А». Но так как он вычисляет лучший маршрут для заданной эвристики, он был назван А*.

Всякой ситуации S, полученной из исходной ситуации в результате определенной последовательности действий, придается численная оценка f ( 5 ) = g (S ) + h( S ), где g(S) — реальная текущая стоимость ситуации S,

h ( S ) — эвристическая функция, которая оценивает стоимость наилучшей последовательности действий, начинающейся с S и заканчивающейся решением.[2]

Следовательно, f ( S ) является мерой стоимости решений, «подчиненных» ситуации S, т. е. решений, включающих то же подмножество исходных действии. Так, например, когда каждому действию соответствует элементарная стоимость f ( S , S ₂, a) , представляющая собой стоимость перехода из S в S с помощью действия а, подсчитать функцию g(S) очень просто: она равна сумме стоимостей действии, которые надо выполнить, чтобы дойти до данной точки от исходной ситуации S. Так как стоимости предполагаются положительными, функция g(S) будет строго аддитивной.

В начале работы алгоритма раскрывается начальный узел, затем просматриваются узлы, смежные с начальным, выбирается тот из них, который имеет минимальное значение f (S), после чего этот узел раскрывается. На каждом этапе алгоритм оперирует с множеством путей из начальной точки до всех ещё не раскрытых (листовых) вершин графа («множеством частных решений»), которое размещается в очереди с приоритетом. Приоритет пути определяется по значению f (S) = g(S) + h(S).

Алгоритм продолжает свою работу до тех пор, пока значение f ( S ) целевой вершины не окажется меньшим, чем любое значение в очереди (либо пока всё дерево не будет просмотрено). Из множественных решений выбирается решение с наименьшей стоимостью. Чем меньше значение f ( S ) , тем больше приоритет.

Алгоритм А* обладает следующими свойствами:

• 1)    Алгоритм A* является полным в том смысле, что он всегда находит решение, если таковое существует.

• 2)    Если эвристическая функция h допустима, то есть никогда не переоценивает действительную минимальную стоимость достижения цели, то A* сам является допустимым (или оптимальным), также при условии, что мы не отсекаем пройденные вершины. Если же мы это делаем, то для оптимальности алгоритма требуется, чтобы h(x) была ещё и монотонной, или преемственной эвристикой. Свойство монотонности означает, что если существуют пути A—B—C и A—C (не обязательно через B), то оценка стоимости пути от A до C должна быть меньше либо равна сумме оценок путей A—B и B—C. (Монотонность также известна как неравенство треугольника: одна сторона треугольника не может быть длиннее, чем сумма двух других сторон). Математически, для всех путей x , y (где y — потомок x ) выполняется:

g ( x ) + h ( x ) <  h ( y ) + h ( y )

• 3)    A* также эффективен для заданной эвристики h . Это значит, что любой другой алгоритм исследует не меньше узлов, чем A* (за исключением случаев, когда существует несколько частных решений с одинаковой эвристикой, точно соответствующей стоимости оптимального пути).[2]

Несмотря на ряд своих положительных свойств, алгоритм очень ресурсозатратен – во многих случаях без дополнительной оптимизации он непригоден для поиска в реальном времени.

Из описания алгоритма А* сделаем вывод, что на основе именно этого алгоритма будет строится решение задачи поиска оптимального пути, так как именно этот алгоритм в силах учитывать уровни сложности прохождения пути разного рода передвижения, имеет способность использовать эвристические функции, характеризующие время прохождения пути автомобиля и пешехода, а так же следует фиксировать длину всего пройденного пути от начала движения до настоящего места нахождения.

Таким образом, алгоритм А* является наилучшим решением поиска оптимального пути. Оптимизировав его, мы сможем справиться с задачей выбора оптимального пути следования при реагировании на ЧС в МЧС.

Geographic Information Systems, search algorithms, optimal route