Исследование модального способа построения Simulink-моделей ПИД-регуляторов для динамических систем первого порядка с транспортным запаздыванием

В работе [1] был разработан модальный метод проектирования ПИД-регуляторов для динамических систем второго и более высокого порядков. Суть модального способа ПИД-регулирования сводится к выбору параметров регулятора таким образом, чтобы его нули и полюса соответствовали полюсам аппроксимируемого полиномами первой или второй степени многомерного объекта. Доказано, что в этом случае обеспечивается наилучшее качество переходных процессов замкнутой регулятором системы.

В настоящей статье ставится задача описания и тестирования предложенного в [1] модального метода проектирования для аппроксимированных систем первого порядка и объектов первого порядка с запаздыванием.

1. МЕТОДИКА МОДЕЛИРОВАНИЯ ПИД-РЕГУЛЯТОРОВ ДЛЯ ДИНАМИЧЕСКИХ ОБЪЕКТОВ ПЕРВОГО ПОРЯДКА И СИСТЕМ

С ЗАПАЗДЫВАНИЕМ

Системы первого порядка и системы, которые могут быть аппроксимированы уравнениями первого порядка, главным образом характеризуются постоянной времени Т передаточной функции (1)

W ( 5 ) =

Ts + 1

Коэффициенты ПИД-регулятора, определяемые по постоянным времени для различных систем первого порядка KP, KI, KD и постоянные времени согласно описанной в [1] методике предлагается определять по формулам:

KT KT

T = — = - = 1, td = — = - = 1,- = —

I KI T D KP T в которых дифференциальная составляющая KD и интегральная составляющая KI корректируются, как показали исследования [1], споправочными коэффициентами a=[0.1, 3] и б=[0.1, 2] соответственно (табл. 1), N-коэффициент коррекции постоянной времени фильтра высоких частот.

Большое число промышленных объектов (например, бортовая инерциальная навигационная система самолета [2]) может быть приближенно смоделировано системами первого порядка с запаздыванием (FOPTD-моделями [2]). FOPDT-модели являются комбинацией моделей

систем первого порядка со звеном постоянного

транспортного запаздывания. Их передаточная

функция задается формулой (2)

W ( 5 ) =

e

Ts + 1

Баканов Максим Витальевич, аспирант.

и представляется s-образной кривой на рис. 1. Она характеризуется двумя константами: временем задержки (постоянной транспортного запаздывания) L и постоянной времени Т объекта первого порядка.

Для расчета коэффициентов ПИД-регуляторов в этом случае предлагается использовать формулы, приведенные в табл. 2.

Для проверки предложенного метода проектирования ПИД-регуляторов, создадим

Таблица 1. Предлагаемые формулы для расчетов коэффициентов ПИД-регуляторов для систем первого порядка

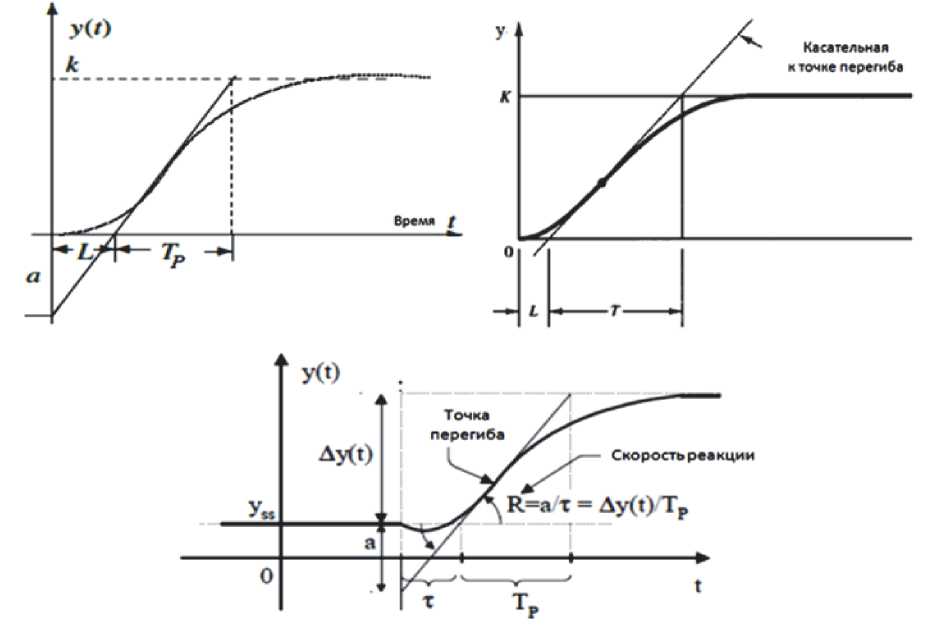
Рис. 1. S- образная крив ая реакции системы с запаздыванием

Объект	Параметры ПИД-регулятора
	KP	KI	KD	т D	TI	N
T	T	а Т	е Т	1	1	2…20
Пределы ограничений	T	а Т а = 0.1...3	е Т е = 0.1...2	е е = 0.1...2	а а = 0.1...3

Таблица 2. Предлагаемые формулы для расчетов коэффициентов ПИД-регуляторов для систем первого порядка с запаздыванием

Объект	Параметры ПИД-регулятора
	KP	KI	KD	т TD	TI	N
T	T	а Т	е Т	1	1	2…20
Пределы ограничений	T	а Т а = 0.1...3	е Т е = 0.1...2	е е = 0.1...2	а а = 0.1...3

Simulink-модель, изображенную на рис. 2, с четырьмя различными аппроксимированными системами, три из которых являются системами первого порядка, а четвертая – описывает процесс первого порядка с транспортным запаздыванием.

2. РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ В СРЕДЕ MATLAB/SIMULINK

При тестировании в среде Matlab предложенного метода проектирования ПИД-регуляторов [1] для систем первого порядка и объекта перво- го порядка с запаздыванием, необходимо применить формулы, приведенные в табл. 2, в виде функции, обозначаемой «PID_method». Значения законов ПИД-регулирования, вычисленные по предложенным формулам, а также величины коэффициентов настройкиKD и KI, ускоряющие реакцию системы и снижающие перерегулирование, приведены в табл.3.

При подстановке вычисленных коэффициентов ПИД в Simulink-модель для наблюдения реакции конкретной системы необходимо производить действия с переключателями ManualSwitch. При этом для каждой системы результаты реакции отображаются при помощи блока Scope в виде графиков, изображенных на рис. 3 и 4.

На рис. 3 изображена реакция системы 1 (sys1) при следующем положении переключателей:

ManualSwitch – вверх, ManualSwitch2 – вверх, а положение ManualSwitch1 произвольно; и значениях коэффициентов, вычисленных в табл. 3 в первом случае. Таким образом, наблюдается воздействие обычного ПИД-регулятора на систему 1 (sys1) по методу Николса - Циглера [1].

На рис. 4 изображена реакция системы 1 (sys1) при следующем положении переключателей: ManualSwitch – вниз, ManualSwitch1 – вверх, ManualSwitch2 – вверх; и значениях коэффициентов, вычисленных в таблице 3 в первом случае. Таким образом, наблюдается воздействие встроенного ПИД-контроллера Simulink на систему 1 (sys1).

На рис. 5 изображена реакция системы 1 (sys1) при следующем положении переключателей: ManualSwitch – вниз, ManualSwitch1 – вниз,

Таблица 3. Вычисленные значения коэффициентов ПИД-регуляторов

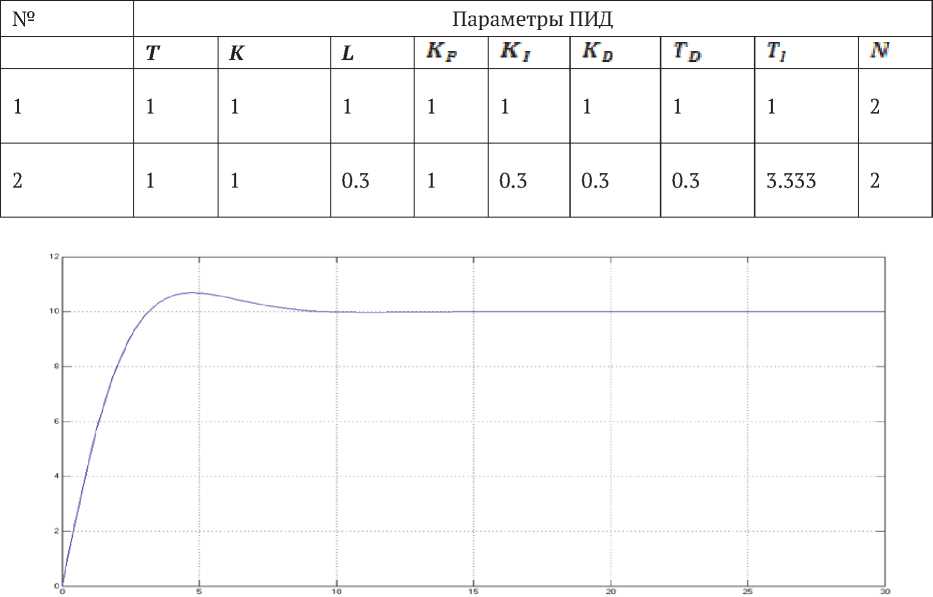
Рис. 3. воздействие обычного ПИД-регулятора на систему 1 (sys1)

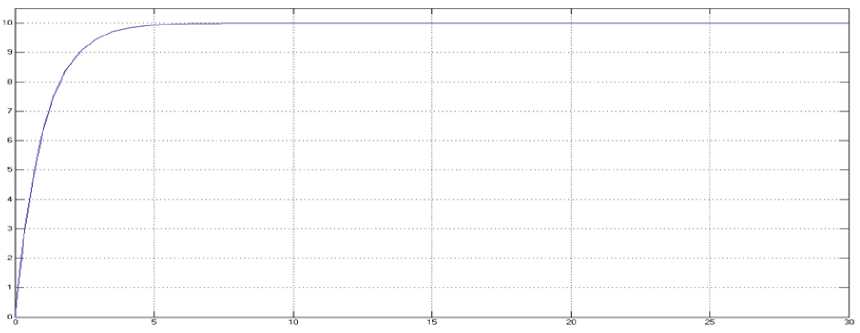
Рис. 4. воздействие встроенного ПИД-регулятора на систему 1 (sys1)

ManualSwitch2 – вверх; и значениях коэффициентов, вычисленных в таблице 3 в первом случае. Таким образом, наблюдается воздействие ПИД-регулятора, смоделированного с учетом фильтра низких частот, на систему 1 (sys1).

На рис. 6 изображена реакция системы 2 (sys2) при следующем положении переключателей: ManualSwitch – вверх, ManualSwitch2 – вверх, а положение остальных переключателей – произвольно; и значениях коэффициентов, вычисленных в табл. 3 во втором случае. Таким образом, наблюдается воздействие обычного ПИД-регулятора на систему 2 (sys2).

На рис. 7 изображена реакция системы 2 (sys2) при следующем положении переключателей: ManualSwitch – вверх, ManualSwitch2

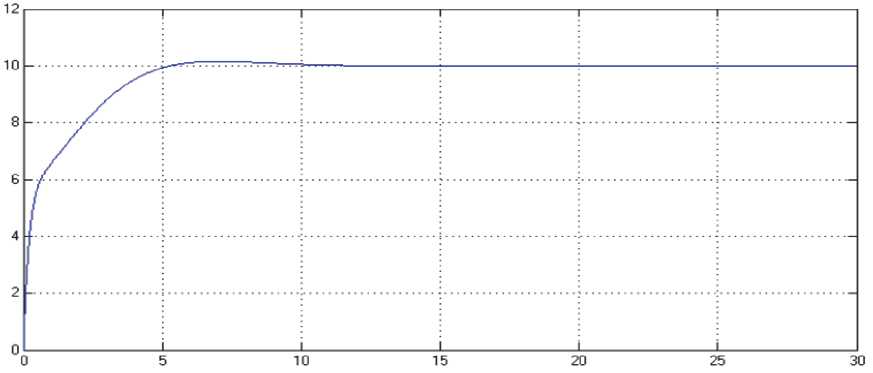
Рис. 5. воздействие регулятора, смоделированного с учетом фильтра низких частот ПИД-регулятора на систему 1 (sys1)

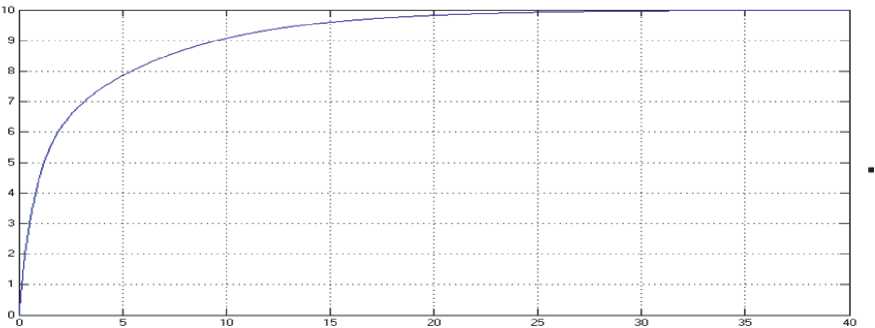
Рис. 6 . воздействие обычного ПИД-регулятора на систему 2 (sys2)

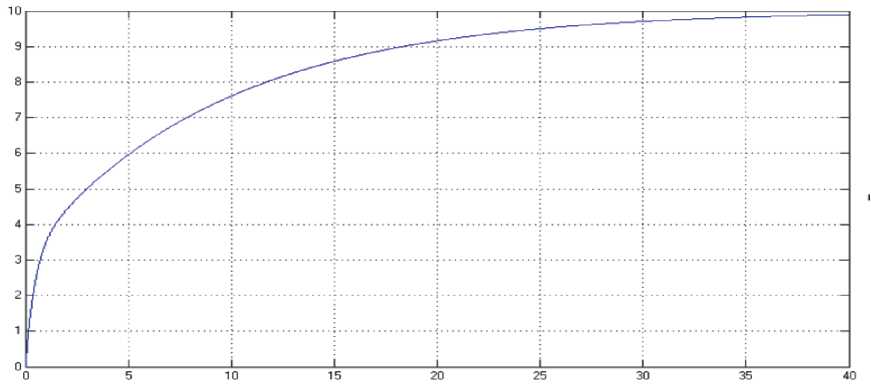
Рис. 7. Воздействие встроенного ПИД-регулятора на систему 2 (sys2)

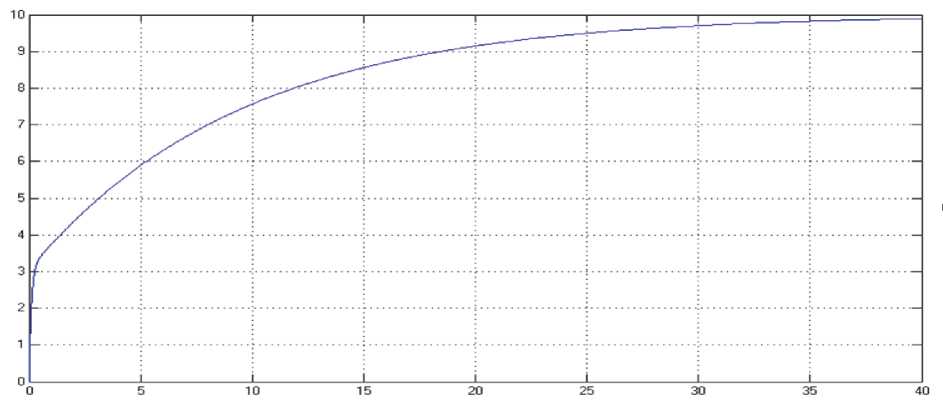
Рис. 8. Воздействие регулятора, смоделированного с учетом фильтра низких частот ПИД-регулятора на систему 2 (sys2)

– вниз, ManualSwitch3 – вверх, а положение остальных переключателей - произвольно; и значениях коэффициентов, вычисленных в табл. 3 во втором случае. Таким образом, наблюдается воздействие встроенного ПИД-регулятора на систему 2 (sys2).

На рис. 8 изображена реакция системы 2 (sys2) при следующем положении переключателей: ManualSwitch – вниз, ManualSwitch1 – вниз, ManualSwitch2 – вниз, ManualSwitch3 – вверх, а положение остальных переключателей - произвольно; и значениях коэффициентов, вычисленных в табл. 3 во втором случае. Таким образом, наблюдается воздействие ПИД-регулятора, смоделированного с учетом фильтра низких частот, на систему 2 (sys2).

ЗАКЛЮЧЕНИЕ

В статье представлены результаты исследований на основе простой и эффективной методики проектирования ПИД-регуляторов, основанной на знании параметров свободного движения объектов. Предложенная модель была протестирована на различных динамических системах, включая системы первого, второго, третьего и четвертого порядков, а также объектов первого порядка с запаздыванием. Приведены результаты численного моделирования: зависимости реакций систем на ступенчатый входной сигнал 10 ^. 1( t ) .

Анализ результатов тестирования показывает, что важным компромиссом моделирования является компромисс между средней быстротой сглаживания выходного сигнала и приемлемым перерегулированием. Это позволяет получить требуемые показатели качества переходных процессов: апериодичность выходного сигнала и минимальное время регулирования, а также определить величину критического транспорт- ного запаздывания, при котором объект управления становится неустойчивым.

Ряд близких и смежных вопросов управления объектами различной природы рассмотрен в работах [3-14].