Исследование моделей и процедур самоконфигурации генетического программирования для формирования деревьев принятия решений в задачах интеллектуального анализа данных

Введение. Алгоритм автоматизированного формирования деревьев принятия решений методом генетического программирования [1; 2] показал свою эффективность при решении тестовых и прикладных задач [3–5]. Следовательно, его дальнейшая модернизация для повышения скорости работы, удобства пользователя и уровня автоматизации является актуальной задачей. Для улучшения алгоритма были рассмотрены и реализованы три процедуры самоконфи-гурации: Population-Level Dynamic Probabilities (PDP), Individual-Level Dynamic Probabilities (IDP) [6] и управление с помощью нечеткого контроллера [7]. Данные процедуры позволят снизить участие пользователя в настройке алгоритма, что, в свою очередь, приведет к повышению скорости работы, удобства интерфейса и уменьшит риск человеческого фактора. Следовательно, данный алгоритм можно будет применять для решения задачи ракетно-космической отрасли, где требуется высокая точность и минимизация рисков.

Population-Level Dynamic Probabilities и IndividualLevel Dynamic Probabilities. Метод PDP работает следующим образом: вероятности использования генетических операторов напрямую зависят от успешности одного или другого оператора, т. е. чем успешнее действие оператора, тем чаще он используется. Вероятности рассчитываются по формуле (1):

ров рассчитываются для каждого индивида отдельно по формуле (2):

p = P all +

(max cntk +1 - cnt 'j) * (100 - n * p all) 1< k < n n *(maxcntk+1) -^^ cnt kj

Г *(100 - n * P all ) scale

success²       20          ⁿ

-----^, P all = —^, scale X r j ^, used -            n           j = 1

где success – это число успешных применений -го оператора; used – общее число применений - го оператора; n – общее число операторов [6; 7].

В методе IDP каждому индивиду популяции присваивается счетчик (cnt j ) по числу неудачных применений оператора. Вероятности применения операто-

20 Pall = —, n где n – общее число операторов [6; 7].

Нечеткий котроллер. Нечеткий контроллер – это регулятор, построенный на базе нечетких правил [8–10]. Общую схему регулятора можно увидеть на рис. 1.

Управление системы на основании нечеткой логики состоит из трех основных этапов:

• 1)    фаззификация;

• 2)    нечеткий вывод;

• 3)    дефаззификация.

На этапе фаззификации четкий вход (информация об управляемом объекте) переводится в нечеткую точку (если вход – скаляр) или точки (если вход – вектор), в соответствии с лингвистическими переменными.

На этапе нечеткого вывода по имеющимся нечетким точкам, полученным на этапе фаззификации, и базе нечетких правил находится нечеткий выход. Нечеткий выход представляет собой нечеткое множество, конкретный элемент которого выбирается на следующем этапе.

На заключительном этапе дефаззификации нечеткий выход, полученный на предыдущем этапе, переводят в четкий, используя соответствующие лингвистические переменные. Существуют несколько возможных вариантов такого перехода, например, первый максимум: из нечеткого множества (нечеткого выхода) выбирают наименьший элемент, принадлежность которого равна максимуму из принадлежностей точек, полученных при фаззификации.

Нечеткий контроллер управляет вероятностями селекции ( p s ), скрещивания ( p c ) и мутации ( p m ) на основании таких показателей, как номер итерации ( N i ), разнообразие популяции ( I i ) и средняя пригодность (sred i ). Общая схема управления представлена на рис. 2.

На рис. 3–5 представлены функции принадлежности для каждого входа и выхода.

В табл. 1–3 представлены базы правил. Формируются они следующим образом. Например, если номер итерации большой и разнообразие популяции не из-

менилось, то вероятность мутации изменяется слабо. Базы правил формулируются на основе многократного решения различных задач и обобщения полученного опыта.

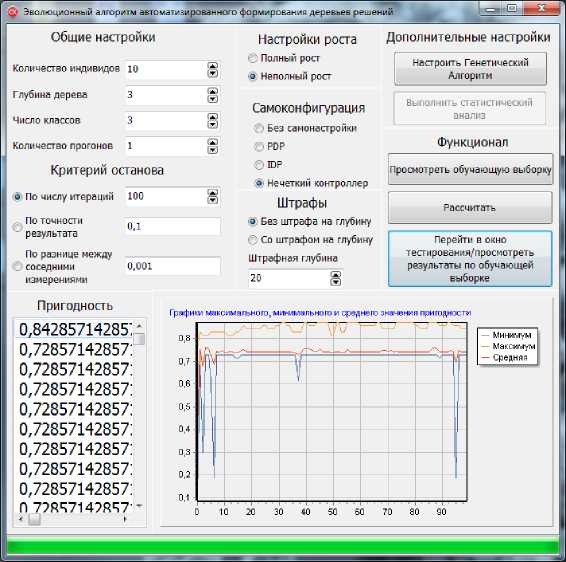
Самоконфигурирующийся гибридный эволюционный алгоритм автоматизированного проектирования деревьев принятия решений. Три настройки были реализованы в существующем алгоритме, главное рабочее окно программы можно увидеть на рис. 6.

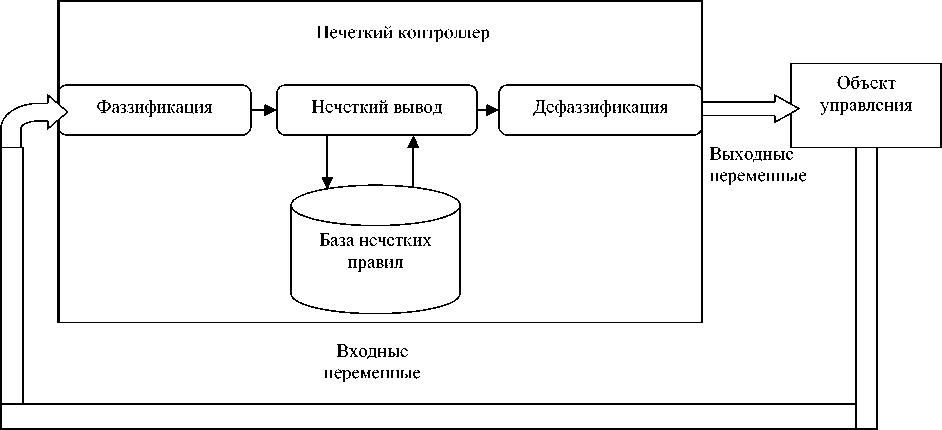
Рис. 1. Схема нечеткого контроллера

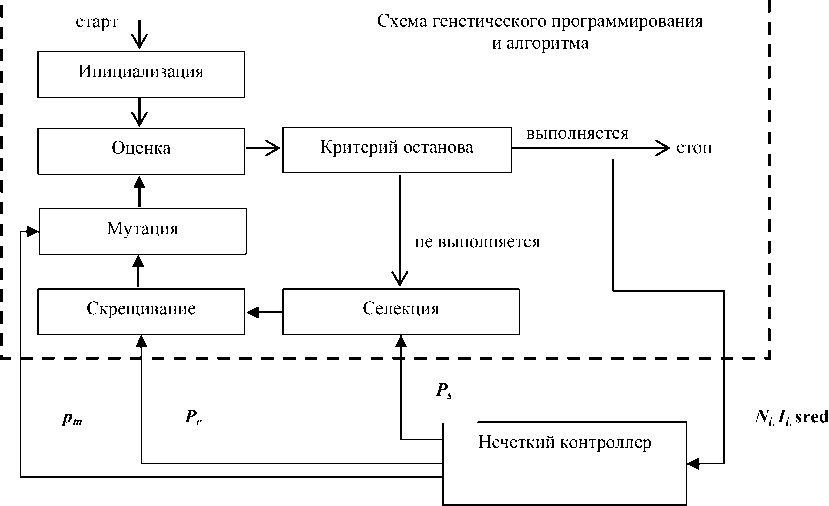
Рис. 2. Общая схема управления

µ ( N i ) t

µ ( I i )

Большой

Маленький

Средний

20 40 60 80

N i

Слабое Среднее Сильное

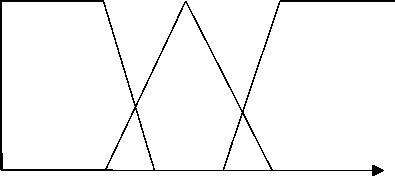
0           0,2 0,4 0,6 0,8            I i

µ (sred i )

Функция принадлежности для номера итерации ( N_i , для 100 итераций)

Функция принадлежности для разнообразия ( I i )

µ ( p m )

Низкая Средняя Высокая

0           0,2 0,4 0,6 0,8             p m

Функция принадлежности для вероятности мутации ( p_m )

Рис. 3. Функции принадлежности входных и выходных параметров

µ ( p s ) A

Маленька я Средняя Большая

0           0,2 0,4 0,6 0,8         sred i

Низкая

Высокая

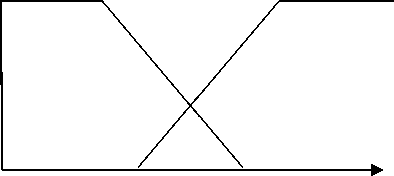
0,4

0,6

P s

Функция принадлежности для средней пригодности (sred _i ) для каждого типа селекции

Функция принадлежности для вероятности селекции ( p_si ) для каждого типа селекции

Рис. 4. Функции принадлежности для каждого входного и выходного параметра селекции

µ (sred i )

µ ( p c )

▲ ^{Маленькая} Средняя Большая

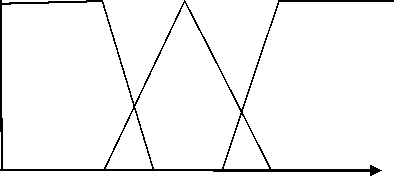
0           0,2 0,4      0,6 0,8          ^sred i

Низкая

Высокая

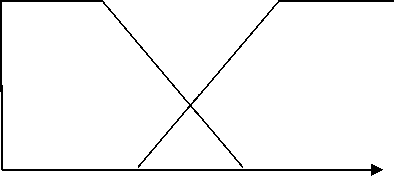
0,4

0,6

P c

Функция принадлежности для средней пригодности (sred _i ) для каждого типа скрещивания

Функция принадлежности для вероятности скрещивания ( p_сi ) для каждого типа скрещивания

Рис. 5. Функции принадлежности для каждого входного и выходного параметра скрещивания

Таблица 1

N i	I i	p m
Если номер большой	и разнообразие сильное	то вероятность мутации не изменяется
Если номер меньше или равен среднему	и разнообразие ниже или равно слабому	то вероятность мутации изменяется сильно
Если номер больше или равен среднему	и разнообразие ниже или равно слабому	то вероятность мутации изменяется средне
Если номер меньше или равен среднему	и разнообразие среднее	то вероятность мутации изменяется средне
Если номер большой	и разнообразие среднее	то вероятность мутации изменяется слабо
Если номер меньше или равен среднему	и разнообразие сильное	то вероятность мутации изменяется слабо

Таблица 2

Sred 1                Sred 2                 Sred 3	P 1          1             P 3            1             P 2
Если средние пригодности одинаковые (большие, средние или маленькие)	то вероятности становятся равными
Если две средние пригодности большие, а одна средняя	то две соответствующие вероятности селекции увеличиваются, а одна уменьшается
Если две средние пригодности средние, а одна маленькая	то две соответствующие вероятности селекции увеличиваются, а одна уменьшается
Если две средние пригодности средние, а одна большая	то две соответствующие вероятности селекции уменьшаются, а одна увеличивается
Если две средние пригодности маленькие, а одна средняя	то две соответствующие вероятности селекции уменьшаются, а одна увеличивается
Если одна средняя пригодность большая, вторая средняя, а третья маленькая	то соответствующие вероятности: увеличивается, не изменяется, уменьшается

База правил для управления скрещиванием

Таблица 3

Sred 1                        Sred 2	P 1	P 3
Если средние пригодности изменились одинаково	то вероятности становятся равными
Если sred 1 > sred 2	то вероятность одноточечного скрещивания увеличивается	то вероятность случайного скрещивания уменьшается
Если sred1< sred2	то вероятность одноточечного скрещивания уменьшается	то вероятность случайного скрещивания увеличивается

База правил для управления мутацией

База правил для управления селекцией

Решение задачи классификации ирисов Фишера и задачи прогнозирования побочных эффектов при лечении эпилепсии. Оценка работоспособности алгоритма с реализованными методами самонастройки была проведена на репрезентативном множестве тестовых задач, решение одной из которых (классификации ирисов Фишера [11]) представлено в табл. 4 для сравнения эффективности настроек. После оценки было проведено исследование предложенного подхода на практической задаче прогнозирования нежелательных явлений при лечении эпилепсии [12]. Для решения этой задачи была построена выборка, содержащая сведения об около ста пациентах. Для каждого пациента в выборке были определены следующие параметры.

• 1.    Входные: пол, возраст, степень обследования, характеристика приступов, МРТ, ВЭМ, терапевтический лекарственный мониторинг, фармакогенетика, вид мутации по трем цитохромам, наличие нежелательных лекарственных явлений.

• 2.    Выходные: группа риска нежелательных явлений и со стороны каких систем организма есть нежелательные явления.

По первому выходу представлены 5 градаций: низкая, средняя, высокая группа риска, не уточнялась и данных для определения недостаточно. Для второго выхода выделены 11 систем: не зарегистрированы нежелательные явления, со стороны центральной нервной системы, со стороны желудочно-кишечного тракта, со стороны эндокринной системы, поражение кожи и ногтей, со стороны мочевыделительной системы, со стороны репродуктивной системы, данных для определения недостаточно, а также есть случаи, когда нежелательные явления проявлялись со стороны нескольких систем одновременно.

Алгоритму были предоставлены достаточные и равные вычислительные ресурсы. Проведены исследования всех трех подходов, получены результаты по 40 запускам для каждого подхода, рассчитываемые по формуле (3), впоследствии усредненные и отраженные в табл. 4. Также в табл. 4 содержится усредненный результат работы алгоритма без самонастройки:

n error = —, n

где error – ошибка классификации; n о – число неверно расклассифицированных измерений; n – общее число измерений.

Статистический анализ результатов. Для сравнения эффективности подходов был проведен статистический анализ [13].

Была выдвинута нулевая гипотеза о том, что нет статистически значимого различия между каждыми двумя генеральными совокупностями, т. е. их математические ожидания равны ( H 0 : M [ X ] = M [ Y ]), при конкурирующей гипотезе, что математическое ожидание первой совокупности больше, чем у второй ( H 1 : M [ X ] >  M [ Y ]). Так как независимые выборки произвольно распределены и их дисперсии неизвестны, но при этом они имеют объем, больше 30 каждая, то выборочные средние распределены приближенно нормально, а выборочные дисперсии являются достаточно хорошими оценками генеральных дисперсий. Тогда можно применить следующий критерий (формула (4)):

X - Y

ID в ( X ) + D в ( Y )

nm

Критическая область в данном случае правосторонняя (рис. 7), уровень значимости равен 0,05, критическая точка равна 1,65 [14; 15]. Значения критерия соответствующих выборок приведены в табл. 5 и 6 (при z набл <  z кр гипотеза H 0 принимается, иначе отвергается).

Таблица 4

Методы/задачи	Классификация ирисов Фишера	Прогнозирование побочных реакций при лечении эпилепсии
Алгоритм без самонастройки	0,044	0,173
IDP	0,02	0,153
PDP	0,022	0,156
Настройка с помощью нечеткого контроллера	0,016	0,132

Результаты работы алгоритма с разными настройками

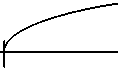
α = 0,05

Z кр = 1,65

Рис. 7. Правосторонняя критическая область

Таблица 5

Попарный статистический анализ для задачи классификации ирисов

	IDP	PDP	Настройка с помощью нечеткого контроллера
Алгоритм без самонастройки	3,28	2,31	5,02
IDP		0,90	1,86
PDP			2,65

Таблица 6

Попарный статистический анализ для задачи прогнозирования побочных явлений

	IDP	PDP	Настройка с помощью нечеткого контроллера
Алгоритм без самонастройки	2,04	1,69	4,37
IDP		0,46	2,38
PDP			2,82

Заключение. Проведенный попарный статистический анализ результатов выявил следующие результаты: алгоритм с любой процедурой самоконфигуриро-вания лучше, чем без нее; управление с помощью нечеткого контроллера лучше, чем методы PDP и IDP, при этом последние не имеют статистически значимого различия между собой, поэтому несравнимы. Следует заметить, что у нечеткого контроллера есть и дополнительные преимущества: прозрачность принятия решения, широкие возможности в управлении (включение перезапуска, добавление новых случайных индивидов и т. д.).

Последующая разработка процедур автоматизированной настройки правил позволит существенно увеличить эффективность алгоритма.