Исследование модифицированной модели Уитли с различным количеством и различными методами формирования элитных особей

Введение. Представлен сравнительный анализ решений модифицированной модели Уитли при различных способах формирования элитных особей. В данном исследовании для формирования элитных особей используются алгоритмы Крона и Плотникова-Зверева. Целями работы являлись разработка модифицированной модели Уитли с применением алгоритмов Крона и Плотникова-Зверева для формирования элитных особей, а также программного средства для решения задачи теории расписаний. Необходимо было получить лучшее решение этой задачи при различных исходных данных с последующей обработкой результатов и выявлением модификации модели Уитли. Описана задача, которая подразумевает поиск оптимального распределения работ по процессорам с минимизацией максимального времени выполнения работ.

Материалы и методы. Приведено описание всех алгоритмов, которые были реализованы при разработке программного средства решения задачи оптимизации построения расписания. Разработаны следующие алгоритмы: модифицированная модель Уитли, применение стратегии элитизма, алгоритм Крона, алгоритм Плотникова-Зверева. Результаты исследования. Разработано программное средство, с помощью которого проведён вычислительный эксперимент при различных исходных данных, с использованием одной, двух, трёх и четырёх элитных особей. Вычислительный эксперимент проведён для наиболее распространённых наборов данных при различном количестве элитных особей. Каждая модификация модели Уитли запускалась сто раз с каждым набором исходных данных. В результате сравнительного анализа было выявлено, какое влияние оказывает использование рассмотренных стратегий элитизма в разработанных модификациях генетического алгоритма (модели Уитли) на точность решения однородной минимаксной задачи при различном количестве элитных особей.

Обсуждение и заключения. Определены лучшие результаты работы алгоритмов, выявлена эффективность применения элитизма в модифицированной модели Уитли при

Introduction. A comparative analysis of the modified Whitley model solutions through different methods of forming elite individuals is presented. The algorithms of Kron and Plotnikov-Zverev are used in the study for the formation of elite individuals. The work objectives are the development of the modified Whitley model involving the Kron’s and Plotnikov-Zverev’s algorithms to form elite individuals, as well as a software tool for solving the scheduling theory problem. It was necessary to obtain the best solution to this problem with various initial data followed by processing the results and identifying a modification of the Whitley model. The distribution problem which implies the search for the optimal distribution of work to the processors with the minimization of the maximum execution time is described.

Materials and Methods. All the algorithms implemented under the development of the software tool for solving the optimization scheduling problem are considered. The following algorithms are presented: the modified Whitley model, the application of the elitism strategy, the Kron’s algorithm, the Plotnikov-Zverev’s algorithm.

Research Results. A software tool is developed. It was applied to conduct a computational experiment with various initial data using one, two, three, and four elite individuals. The experiment was carried out for the most common data sets with a different number of elite individuals. Each Whitley model modification was launched a hundred times with each set of the source data. The comparative analysis of the results shows how the application of the considered elitism strategies in the developed modifications of the genetic algorithm (Whitley model) affects the accuracy of the solution to the homogeneous minimax problem with a different number of elite individuals.

Discussion and Conclusions. The best results of the algorithms are determined; the utilization of elitism in the modified Whit-

Машиностроение и машиноведение

*

∗∗

решении однородной минимаксной задачи теории распи-     ley model when solving a homogeneous minimax problem of саний. Проведено сравнение результатов работы алгорит-      scheduling theory is estimated. The algorithm results are com- ма при одной, двух, трёх и четырёх элитных особях.             pared for one, two, three and four elite individuals.

алгоритмы, вычислительный эксперимент.

Образец для цитирования: Кривошей, Н. С. Исследова-      For citation: N. S. Krivoshey, V. G. Kobak. Study on modi- ние модифицированной модели Уитли с различным коли-     fied Whitley model with different number and various meth- чеством и различными методами формирования элитных      ods of forming elite individuals. Vestnik of DSTU, 2018, vol.

10.23947/1992-5980-2018-18-2-223-229

Введение. Одними из наиболее часто решаемых задач теории расписаний являются NP-полные задачи. Для них практически невозможно подобрать решение за полиноминально быстрое время [1]. Так как в последние годы все более широкое распространение получают многопроцессорные, многомашинные вычислительные комплексы, объединённые в единую вычислительную систему, необходимость поиска наилучшего распределения заданий между процессорами является актуальной и обосновывается возможностью существенной экономии машинного времени. Теоретическая сложность нахождения наилучшего распределения связана с решением экстремальных задач комбинаторного типа, требующих больших вычислительных ресурсов. Генетические алгоритмы, моделирующие эволюционные процессы, являются перспективным способом решения подобных задач [2]. Основным механизмом эволюции является сочетание генетического механизма передачи наследственности, механизма мутаций, обеспечивающих разнообразие видов, и естественного отбора, который обеспечивает с течением времени формирование особей популяции, наиболее приспособленных для данной среды. Более приспособленные особи имеют большую вероятность передать свою наследственную информацию. Наследственная информация в виде хромосомы полностью определяет развитие особи в ее жизненном цикле, и с помощью обмена генами хромосом происходит передача наследственной информации потомкам. Случайные изменения в генофонд вносятся во время мутаций, если новые признаки увеличивают приспособленность особи, то такие признаки скорее всего закрепятся и перейдут к потомкам [3].

Применение стратегии элитизма позволяет дополнительно увеличить скорость схождения алгоритма и, во многих случаях, точность решения [4]. Хотя сама концепция элитизма по сей день является спорной из-за возможности обнаружения алгоритмом решения в локальном экстремуме, во многих случаях она оправдана, и эти случаи можно определить путём сравнения результатов с результатами алгоритма без элитизма в тех же исходных условиях. Обычно в качестве элитной особи выбирается особь с наилучшим значением целевой функции, а модификации алгоритма с применением различных способов формирования элит изучены крайне мало.

Постановка задачи. В вычислительную систему (ВС) из N несвязанных идентичных устройств: P = {p 1 , p₂,™, p n } поступает набор из M независимых параллельных заданий: T = { t 1 , t₂,..., t m }. Известно время решения τ ( t i ) задания t i . При этом каждое задание может выполняться на любом из устройств. В каждый момент времени отдельный процессор обслуживает не более одного задания, выполнение задания не прерывается для передачи на другой процессор. Требуется найти такое распределение заданий по процессорам, при котором суммарное время выполнения заданий на каждом из процессоров было бы минимальным.

Для решения этой задачи хорошо подходят генетические алгоритмы [1, 2]. В данной работе рассматривается решение задачи с помощью модифицированной модели Уитли с использованием элитизма. Комплектование элитных особей реализовывается несколькими различными способами. Задача решается для различных значений параметров M, N и постоянного диапазона времени выполнения заданий .

Краткое описание алгоритмов . Рассматриваемый в данной статье генетический алгоритм (ГА) был описан Уитли (D. Whitley) [5]. Он отличается от классического ГА следующими тремя свойствами:

• •    На каждой итерации только одна случайная родительская пара создает одного потомка.

• •    Ребенок заменяет собой не своего родителя, а одну из наименее приспособленных особей в популяции (первоначально — наихудшую).

• •    Отбор особи для замены производится по ее ранку (рейтингу), а не по приспособленности.

Таким образом, алгоритм включает следующие шаги:

• 1.    Формирование начального поколения;

• 2.    Пропорциональный отбор и последующее применение генетических операторов (в данной модификации — это одноточечная мутация и одноточечный кроссовер с выбранной вероятностью);

• 3.    Проверка условия останова алгоритма (если неуспешна, переход на шаг 2);

• 4.    Лучшая особь является решением задачи.

В исследуемой модификации алгоритм завершает работу, если в течение заданного количества поколений не происходит никаких улучшений показателей приспособленности.

В разработанной в рамках исследования модифицированной модели алгоритма Уитли применяется стратегия элитизма. Элита — это лучшая по приспособленности особь текущего поколения, переходящая в следующее поколение без изменений, она не участвует в селекции и последующем скрещивании [6, 7].

Алгоритм Крона . Принцип работы данного алгоритма заключается в случайном распределении всех заданий на множество процессоров, вычислении общего времени загрузки по каждому процессору { Ti }( i =1.. n ) и выполнении обмена заданиями между процессорами с максимальным Tmax и минимальным Tmin значениями из набора { Ti } при выполнении условия | qkmax - qjmin | <  D , где D = Tmax - Tmin , k , j = 1,2.. m . После каждой из операций обмена значения { Tk } пересчитываются, снова выбираются два процессора с Tmax и Tmin и алгоритм проверки описанного выше условия повторяется. Алгоритм завершится, когда условие ни разу не выполнится [8, 9]. Таким образом, первый этап алгоритма включает шаги:

• 1.    Генерация случайного числа pi — номер прибора равномерно распределённого на интервале [1, N ]. Инициализация j = 1.

• 2.    Назначение на прибор с номером pi j -ого задания. Увеличение счётчика j = j + 1.

• 3.    Проверка, является ли значение j большим , чем количество заданий M , если условие выполняется, то завершить распределение, иначе перейти к шагу 1.

Второй этап включает следующие шаги:

• 1.    Вычисление времени загрузки каждого процессора { Tj } ( j = 1,.., N ) путем суммирования времен выполнения заданий загруженных в каждый j -й прибор.

• 2.    Из итогового множества { Tk } выбираются номера процессоров с максимальным Tmax и минимальным Tmin значениями из{ Tk } соответственно.

• 3.    Для каждого из процессоров с минимальной и максимальной загрузкой проверяется условие по принципу каждый с каждым: tkmax – tlmin <  Δ , где Δ = Tmax - Tmin, k , l = 1,.., M . При этом tkmax > tlmin .

• 4.    Обмен значения tk и tl местами и переход к шагу 1.

Если оно выполняется, то происходит переход к следующему шагу, а иначе выполнение алгоритма прекращается.

Блок схема алгоритма представлена на рис. 1.

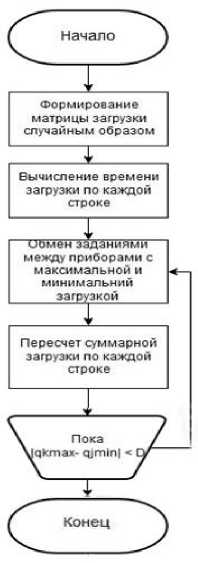
Рис.1. Блок-схема алгоритма Крона / Fig. 1. Flowchart of Kron’s algorithm

Машиностроение и машиноведение

Алгоритм В. Н. Плотникова-В. Ю. Зверева . Широкое распространение имеют простые и достаточно эффективные списочные алгоритмы построения расписаний, основанные на эвристических алгоритмах. Одним из них является алгоритм, предложенный В. Н. Плотниковым и В. Ю. Зверевым. Это приближенный метод для поиска близкого к оптимальному решению, использующий минимаксный критерий [10]. Он выключает следующие шаги:

• 1.    Упорядочить строки матрицы по убыванию сумм всех элементов строки n              n                     n

• 2.    В преобразованной матрице выделить первую строку i =1 и найти в ней min(x (t 1 P j )) — минимальный элемент. Этот элемент принимается за элемент распределения и прибавляется к соответствующему элементу второй строки min(i (t 1 p j ))+ (т (t₂ P j )).

• 3.    Вторая строка теперь учитывает предыдущее решение. Из нее выбирается минимальный min(T (t₂P j )), нужно прибавить его к соответствующему элементу третьей строки min(T (t₂ P j ))+ (т (t₃ P j )) и т.д., в результате получим матрицу Т_т ” .

• 4.    На выполнение передаётся минимальный элемент строки min(T ” (t i P j )), такой что min(T (t i P j )) + 0.

2c(tiPi)) > ^ (T(t2Pi)) > "’ > 2 (^^Pi))-

7=1            i=i                   i=i

Данный алгоритм отличается наибольшим по сравнению с точными быстродействием, простотой и позволяет получить приемлемые по точности решения [10]. Блок-схема алгоритма представлена на рис. 2.

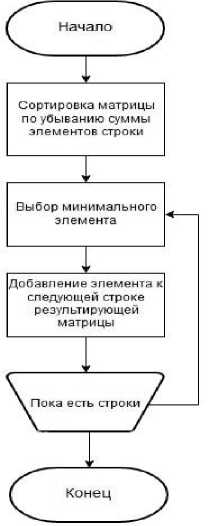
Рис. 2. Блок-схема алгоритма Плотникова-Зверева

Fig. 2. Flowchart of Plotnikov-Zverev’s algorithm

Результаты исследования. Аналитическое определение степени влияния способа формирования элитных особей на результат работы генетического алгоритма не представляется возможным, поэтому с помощью программного обеспечения, реализованного в среде Microsoft Visual Studio 2012 на языке Visual C++, был проведен вычислительный эксперимент.

Разработаны 3 модификации модели Уитли:

• 1.    Элитой полагается лучшая особь исходного поколения;

• 2.    Элита формируется алгоритмом Крона;

• 3.    Элита формируется алгоритмом Плотникова-Зверева.

Массив заданий случайным образом генерируется из заданного диапазона значений (20–30). Вероятности кроссовера и мутации равны 100%. Условие остановки (количество поколений c неизменным Тmax) — 10. Эксперимент был проведён для наиболее часто встречающегося количества процессоров (N) — 2–4 и количества задач (M) — 19, 119, 519. Результаты работы при 1–4 элитных особях приведены в таблицах 1–4. Tmaxm — среднее значение из 100 повторений алгоритма.

Таблица 1

Table 1

Средние значения Тmax (1 элита)

Average values of Tmax (1 elite)

Таблица 2

Table 2

М	N	Алг. Плотникова-Зверева		Алг. Крона		Лучшая особь
		Тmaxm	t, c	Тmaxm	t, c	Тmaxm	t, c
19	2	241,55	0,007	241,03	0,009	245,25	0,005
	3	167,81	0,006	165,19	0,013	168,34	0,006
	4	124,19	0,008	124,57	0,012	125,25	0,005
119	2	1520,14	0,025	1517,62	0,051	1519,91	0,035
	3	1014,28	0,070	1014,75	0,081	1016,79	0,039
	4	767,33	0,051	766,98	0,073	769,19	0,030
519	2	5510,22	0,199	5513,19	0,211	5517,09	0,105
	3	4409,15	0,179	4409,99	0,199	4416,21	0,109
	4	3325,71	0,199	3324,99	0,407	3325,97	0,149

Средние значения Тmax (2 элиты)

Average values of Tmax (2 elites)

М	N	Алг. Плотникова-Зверева		Алг. Крона		Лучшая особь
		Тmaxm	t, c	Тmaxm	t, c	Тmaxm	t, c
19	2	240,52	0,007	240,07	0,011	242,29	0,005
	3	161,31	0,006	162,11	0,013	162,54	0,006
	4	122,59	0,007	122,57	0,014	123,25	0,006
119	2	1520,44	0,028	1518,69	0,057	1520,94	0,041
	3	1012,22	0,087	1012,72	0,089	1025,72	0,042
	4	763,31	0,056	763,93	0,093	764,15	0,035
519	2	5509,25	0,211	5508,02	0,261	5510,09	0,111
	3	4406,55	0,176	4407,96	0,237	4407,91	0,117
	4	3318,75	0,195	3317,95	0,426	3318,98	0,145

Таблица 3

Table 3

Средние значения Тmax (3 элиты) Average values of Tmax (3 elites)

М	N	Алг. Плотникова-Зверева		Алг. Крона		Лучшая особь
		Тmaxm	t, c	Тmaxm	t, c	Тmaxm	t, c
19	2	242,85	0,006	242,53	0,009	242,85	0,006
	3	168,88	0,006	168,18	0,017	168,94	0,006
	4	125,15	0,008	126,58	0,015	127,95	0,006
119	2	1524,16	0,027	1514,12	0,058	1516,31	0,036
	3	1016,26	0,075	1016,25	0,071	1019,19	0,036
	4	767,31	0,055	767,18	0,079	768,69	0,038
519	2	5515,24	0,193	5515,18	0,251	5517,19	0,115
	3	4409,96	0,178	4409,91	0,199	4410,25	0,106
	4	3326,76	0,159	3326,95	0,409	3326,99	0,141

Машиностроение и машиноведение

Таблица 4

Table 4

Средние значения Тmax (4 элиты)

Average values of Tmax (4 elites)

М	N	Алгоритм Плотникова-Зверева		Алгоритм Крона		Лучшая особь
		Тmaxm	t, c	Тmaxm	t, c	Тmaxm	t, c
19	2	243,43	0,007	242,73	0,009	245,24	0,006
	3	168,78	0,006	167,15	0,011	168,39	0,006
	4	126,15	0,009	126,27	0,011	126,29	0,005
119	2	1525,17	0,026	1524,68	0,031	1525,34	0,022
	3	1017,27	0,049	1017,96	0,081	1017,29	0,034
	4	769,35	0,037	767,93	0,071	771,49	0,034
519	2	5512,21	0,159	5510,59	0,201	5515,44	0,185
	3	4415,13	0,158	4411,09	0,161	4415,29	0,169
	4	3327,77	0,168	3329,19	0,372	3331,47	0,209

Заключение. Из полученных результатов видно, что средние значения Tmax , полученные с использованием алгоритмов Крона и Плотникова-Зверева для формирования элиты, во всех случаях являются лучшими по отношению к результатам работы алгоритма с обычным элитизмом. С увеличением количества элит эффективность алгоритма Крона становится более выраженной, при этом время работы генетического алгоритма увеличивается не слишком существенно.