Исследование наборов твердооксидных топливных элементов в пакетном исполнении

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 622.621.46                                     

Основной целью выполнения настоящих исследований и вычислительных является определения ресурса безаварийной эксплуатации ТОТЭ пакетного исполнения. Причем этот ресурс должен соответствовать периоду времени от начала эксплуатации до момента одновременного наступления деформационных осложнений (по устойчивости и прочности) в поведении ТОТЭ пакетного исполнения. Это означает что необходимо разработать регламент на проектирование ТОТЭ в пакетном исполнении для определения их конструкций,

[(cc)   ® I обеспечивающих деформационное функционирование пакета ТОТЭ в установленных пределах эксплуатации. Достижения установленных целей обеспечивается путем решения задачи устойчивости и прочности в отдельности и совместного анализа их результатов: задача устойчивости для ТОТЭ в пакетном исполнении. Предполагается, что пакет выполняется из прямоугольных пластин, представляемых отдельными планарными ТОТЭ. Положение отдельных пластинок ТОТЭ зафиксированы в пакете специальным ограничителем-рамкой [1–8].

Предполагается, что теплофизические свойства ограничителя отличаются от свойств собранных в пакет пластин, а именно коэффициент его температурного расширения значительно меньше аналогичного показателя пластин. Ширина и длина собранных в пакет пластинок обозначены, соответственно, «а» и «в». Предполагается также, что собранных в пакет пластинок физико-механические и тепла-физические свойства с учетом возможных отклонений при реализации технологических регламентов их изготовления могут существенно различаться. Поэтому для этих показателей с учетом количества пластинок в пакете приняты соответственно, обозначения Е i , V 1 , α i , Е z , Ƴ 2 , α 2 , E n , V 2 , E n , V n , α n , где Е i , — модуль упругости, α i — коэффициент температурного расширения i-той пластины.

Для обозначенного варианта исполнения пакета пластинок требуется определить предельное значения операционный температуры, при достижении которой произойдет потеря устойчивости отдельных пластинок в пакете. Это состояние и дальнейшая эксплуатация пакетного исполнения ТОТЭ будет способствовать снижению КПД в целом, так и математическое моделирование задачи.

С учетом принятого допущения о том, что коэффициенте температурного расширения ограничителя-рамки значительно меньше значения этого показателя собранных в пакет пластинок предполагается, что при высокой операционной температуре генерируемого при эксплуатации энергоустановок, ограничитель-рама не деформируется. Пластины ТОТЭ, установленные в пакет, представляются элементами конструкции, толщины которых значительно меньше других их размеров, т е длины и ширины. Следовательно, расширения подобного конструктивного элемента в направлениях перпендикулярной ее оси в плоскости можно принимать во внимание. Материалы, из которых изготавливаются отдельные пластины, собранные в пакет, рассматриваются как однородные и изотропные.

Методы решения задачи

Для решения задачи при принятых выше допущениях задачи применены метод сечений и принцип независимости действия сил.

Решение задачи . Рассматривается, как указано выше «а» и «в» заключенных в ограничительную раму (Рисунок 1).

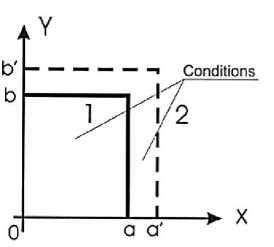
Согласно методу сечений предполагается отсутствие ограничительной рамы, поддерживающей собранные в пакет пластины. В этом случае, т. е. при отсутствии ограничительной рамы относительное удлинение i -той пластинки в пакете может представлено выражение вида:

E j = а_г T ( i е n ) , (1)

где T — значение операционный температуры, воздействию которой одинаково подвергаются все элементы пакетного исполнения ТОТЭ.

Состояние пластинок в пакетном исполнении 1,2 до соответственно и после деформационного состояния i -той пластины в пакете.

При достижении температурного фактора уровня операционной размеры пластин с учетом термовоздействия в свободно состоянии без ограничительно рамы могут быть определены как а1=а(1+αiT)                                               (2)

b¹=b(1+α i T)

Следовательно, в реальности если принять тот факт, что длина т =пластинок уменьшается на величину, равную b' - b = b a T , то ширина пластинок будет увеличиваться До a a T + v b a T = ( a + v b ) a T

Таким образом, относительные удлинения ширины и длины пластинок, соответственно, можно представить в виде

£

£ yi

| 1 + v.— \a.T ii

k     a J

I 1 + v. a^\aT ii

k     b J

i — 1,..., n

Если предположить, что потеря устойчивости пластинок в пакетном исполнении происходит в упругой области деформаций, где связи между деформациями и напряжениями подчиняются закону Гука, тогда для определения напряжений могут быть записаны ниже приводимые зависимости:

i — 1,..., n

a — E 1 + v — \aT;

xi             i                i             i

k     a J

(     a ^ T

a — E 1 + v — aT.

yi             i                i             i .

где _a , _a — соответственно, значения напряжений вдоль координатных осей « х » и « у »

Аналогично, силы, действующие на поверхностях пластинок, могут быть определены выражениями вида

b ^

P = Es S = E 1 + v.— \aT ■ b ■ h ;

xi            i xi x            i               i             i                  i к     a J

P = e s S = E \ 1 + v. a \a.T ■ b ■ h . yi            i yi y            i               i             i                  i

где hi — толщина i-той пластины в пакете, Sx, Sy — площади поперечных сечений, соответственно, в направлениях перпендикулярных осям «x» и «y».

Если принять предложения о том, что при пакетном исполнении реализовался вариант конструкции, с размерами b> а , то потеря ее устойчивости будет происходить в направлении оси « y ».

Известно, что при оценке работоспособности конструкций по деформационному явлению устойчивости соответствующее поведение определяется значением критической силы по Эйлеру, т. е. по формуле

П ²EJ i mn ^kp          b²      ,

где Ji min — минимальное значения момента инерции поперечного сечения элемента конструкции, в нашем случае i -этой деформируемой в пакете пластины.

Следует отметить, что конструктивное исполнение пакета пластинок дает основание для предложения о существовании более благоприятного режима деформирования внутренних пластинок, по сравнению с крайними в общем пакете.

Это означает, что внутренние пластинки в общем пакете взаимодействия друг с другом поддерживаются соседними пластинками т. е деформированные поведения «i»-го и «j»–го слоев накладываясь ограничивают деформации внешние или крайние пластины имеют одностороннюю поддержку и поэтому лишены возможности поддерживаться с обеих сторон, что делает их более уязвимыми в деформационном поведении пластинок в пакетном исполнении.

Таким образом, с учетом содержания поставленной задачи из условия равенства (5) и

E , 1 + v - a Tah

n2 EJ i x min

i

к

i b J

ii

b ²

критическое значение операционной температуры из

последнего для реализуемой конструкции пакетного исполнения ТОТЭ может быть определено по ниже приводимому выражению:

T kr

n ² h ²                   ah³

__________i ______ где j =    ■

12 b ( b + v-) a      x min    12

.

Как следует из (7) значение операционный температуры, соответствующее критическому состоянию пакетного исполнения ТОТЭ прямо пропорционально квадрату толщин (hi2) пластинок в пакете и обратно пропорционально их метрическим размерам («а» и «b») и коэффициенту термического расширения («αi»). Существенным является то, что на величину критической температуры не влияют механические свойства. («Еi») материалов изготовления пластинок пакетного исполнения ТОТЭ. Следует принять во внимание и тот факт, что при значительно высоких соответствующих и сопровождающих эксплуатационные циклы ТОТЭ и операционных температурах коэффициент Пуассона для всех материалов принят равным ν → 0,5 . Это означает, что на значения температуры, определяющее критическое деформационное поведение ТОТЭ пакетного исполнения механические характеристики материалов изготовления пластинок не влияют и оно может быть определено с учетом их метрических и теплофизических характеристик. Полученные результаты позволяют сделать нижеприводимые обобщения для практики проектирование пакетов ТОТЭ и управления их деформационным поведением:

• -    при одинаковых метрических размерах и теплофизических свойствах материалов изготовления более уязвимыми в деформационном поведении являются крайние конструктивные элементы пакетного исполнения планарных ТОТЭ;

• -    более чувствительными в определении значения температур, соответствующих критическому деформационному поведению пакетного исполнения планарных ТОТЭ пакетного исполнения из метрических характеристик, являются толщины его конструктивных элементов. Причем, эта зависимость является квадратичной, что делает необходимым использование в пакете в качестве крайних конструктивных элементов с большими толщинами;

• -    при одинаковых метрических размерах для повышения термоустойчивости планарных ТОТЭ в пакетном исполнении необходимо при их проектировании использование элементов отдельных (ТОТЭ) с относительно низкими коэффициентами температурного расширения;

• -    уменьшение метрических размеров (длины и ширины) планарных ТОТЭ в пакетном исполнении способствует увеличению термической устойчивости конструкции причем на этой зависимости никак не отражаются механические характеристики материалов изготовления отдельных элементов (отдельных ТОТЭ).

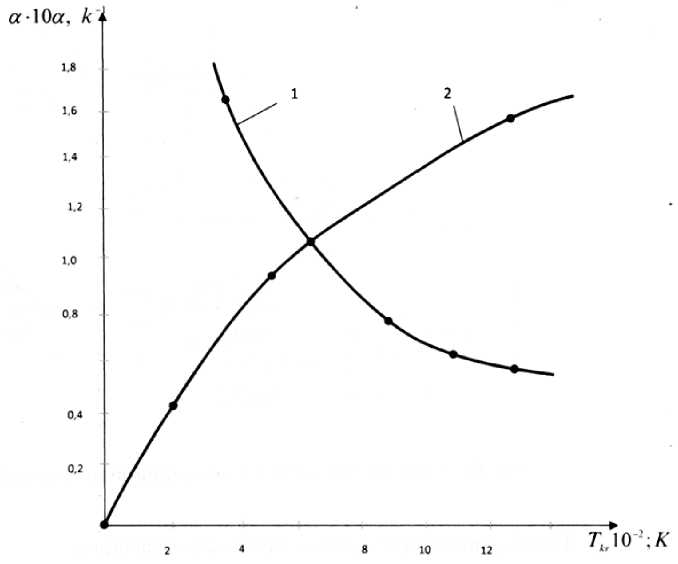
Рисунок 2. Зависимость температуры термоустойчивого пакета пластинок от их коэффициента термического расширения материального исполнения (кривая 1) вычислялась для α=0,1 и метрических характеристик (кривая 2 вычислялась для α i =1,2×10^-5k^-1)

Выше приводятся зависимости критической температуры [ а = а(Т_кр ) ]

коэффициента термического расширения от и допустимых температурных нагружений от метрических характеристик

Tkp = Tkp(v) Для планарного ТОТЭ пакетного исполнения с тремя конструктивными элементами (Рисунок 2).

Сделано предположение о том, что серединный элемент имеет меньшую толщину по сравнению с крайними и приняты обозначения вида a = ь • у = h • v = 0,3; _п ² = 10 . a

Следует отметить, что при эксплуатации ТОТЭ в пакетном исполнении не исключается потеря прочности и разрушения от воздействия температурного фактора конструктивных элементов до потери их устойчивости. Этой случай тоже может быть классифицирован как возникновение деформационного осложнения в эксплуатационном процессе установки. Наступление подобного осложнения будет способствовать уменьшению КПД установки, что несомненно станет причиной снижения показателей ее эффективности.

Поэтому необходимо поддерживать и обеспечивать эксплуатационный процесс технологическими параметрами, исключающими подобное деформационное осложнение. Для решения этой задачи ниже рассматривается задача прочности многоэлементного пакета установки ТОТЭ, для чего общая толщина пакета обозначена H =^п ; где n — количество i = 1

пластинок в пакете. Согласно механической модели на Рисунке 3 определены силы и напряжения, действующие по направлениям осей « x » и « y » нижеприводимыми зависимостями:

а

Z Ej | 1 + v;. — Ьа • T • b • h i=1    I          a )

H

а

n

Z E1

i = 1

a

1 v ib

^а 1

• T • a • h

H

Для оценки прочности используются условия прочности при плоском напряженном состоянии вида

J2 + 2(1 + v)J2 =а2

где J1, J2 — соответственно, первый и второй инварианты напряжений, определяемые как j = a + a ; j = -a •^ ; a и v — соответственно, приведенные предел текучести и 1       x       у’     2         x     y     T коэффициент Пуассона материального исполнения элементов пакета, определяемые как:

GT

n

Za iT • hi i=1

H

;

v =

n

Zvi • h1

i = 1

H

^_т и vi — соответственно предел текучести и коэффициент Пуассона i -ой пластины.

С учетом введенных обозначений после несложных преобразований для определения критической температуры соответствующей потере прочности элементами ТОТЭ пакетного исполнения получается нижеприводимая зависимость:

T kp

K д/(A + B)2 - 2(1 + v)AB ’

где

„(,      a I

A = aYE 1 + v • a. ■ h i     i      11

i=1   V        Ь J nb

B=b Ё E 1+vi- Ьа • hi i=1    V        a J

k=i °л i =1

Как следует из полученных зависимостей предел температурной прочности элементов ТОТЭ в пакетном исполнении определяется наряду с метрическими характеристиками конструкции исключительно физико-механическими свойствами их материального исполнения. Как было отмечено выше, что полный эксплуатационный ресурс планарного ТОТЭ в пакетном исполнении может быть обеспечен при технологических режимах, способствующих появлению деформационного осложнения, потерей и одновременно устойчивости элементов и появлениям пластичности в их материальном исполнении.

Поэтому решения задачи обеспечения использования существующего механического потенциала для ТОТЭ в пакетном исполнении является весьма важной в определении рациональных метрических характеристик его конструкции. Эти характеристики могут быть определены путем анализа результатов задач для устойчивости и прочности. С этой целью следует приравнять выражения (7) и (9).

n² h²      ₌__________k __________ (11)

12 b(b+v • a a  j(a + в )2 - 2(1 + v Ab или для пакета квадратной формы n2 h2     =      k                                            (12)

12 a2 (1 + vi )a   A 7 4 - 2(1 + v)

Если учесть, что при появлении пластичности в материалах независимо от его остальных механических характеристик v = v = 0,5, тогда (12) вырождается в зависимость вида nh =K                                     (13)

18 a2 a A где

A = 1,5 a j^ E, a h

K = H a

Tnp

Для a = a = a = 1,2 •ю ^{- 5} k ^{- 1} после несложных преобразований для проектирования планарного ТОТЭ в пакетном исполнении между метрическими, теплофизическими и механическими характеристиками получается нижеприводимая зависимость

Y = 10aaP или a

10 - 5 Y 2

,

P

p = Tnp - который может быть представлен значение P = 3 • 10 3. k — коэффициент E np термического расширения, 1/к.

С учетом последнего при значениях α i =1,2×10^-5k^-1 может быть определена рациональная геометрическая характеристика для планарного ТОТЭ в пакетном исполнении, т. е. γ i >6×10^-2.

Эта означает, что если относительная толщина крайнего элемента пакета ТОТЭ планарного исполнения γ i >6×10^-2, то наступившее деформационное осложнение будет характеризоваться потерей устойчивости конструкций. В противном случае, т. е. при γ i <6×10^-2, то элементы ТОТЭ пакетного исполнения могут потерять устойчивость после появления пластичности в их материалах. Следовательно, только при γ i =6×10^-2 может быть достигнута (конечно, для принятых значений параметров, входящие в полученные зависимости) использование потенциалов конструкции как по устойчивости ее элементов, так и по прочности их материалов.

Значение параметра γ, как видно из (Рисунок 3), может изменяться для различных уровней температурного нагружения. Причем результаты анализа приведенных кривых свидетельствует, что для операционных температур (600–1000)K приведенный физический параметр «а» изменяется в переделах от ( 0,35 ^ 0,18 )^ 10 ^{- 5} K ^{- 1} уменьшается, примерно на 65%. Таким образом, эти результаты могут быть использованы для определения с приемлемым деформационным поведением конструкций при заданных их метрических характеристиках и теплофизических свойств материального исполнения.

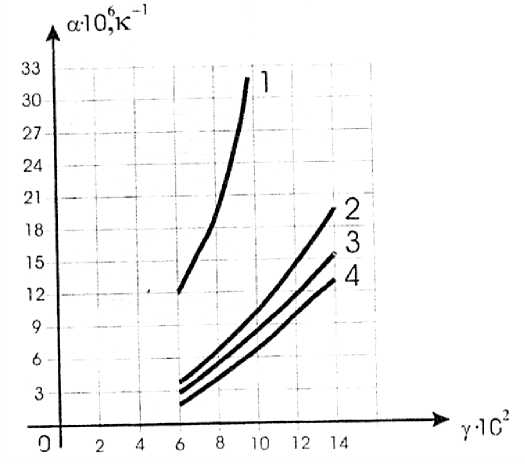
Рисунок 3. Изменение метрических характеристик конструкции от теплофизических свойств материалов: 1 — (Т=200°С); 2 — (Т=600 °С); 3 — (Т=800°С); 4 — (Т=1000°С)

Вывод

Это означает что если относительная толщина крайнего элемента пакета ТОТЭ планарного исполнения γ i >6×10^-2, то наступившее деформационное осложнение будет характеризоваться потерей устойчивости конструкции. В противном случае, т. е. при γ i <6×10^-2 элементы ТОТЭ пакетного исполнения могут потерять устойчивость до появления пластичности в их материалах. Следовательно только, при γ i =6×10^-2 может быть достигнута использование потенциалов конструкций как по устойчивости ее элементов, так и по прочности их материалов.