Исследование напряженно-деформированного состояния сечения численным экспериментом

Бюллетень науки и практики / Bulletin of Science and Practice

УДК 624.07+721.011                                 

Для исследованию железобетонных одномерных конструкций и деформативности бетона посвящены работы В. Н. Байкова, В. Я. Бачинского, А. А. Беспаева, С. В. Бондаренко, И. С. Воронюк, А. А. Гвоздева, А. Л. Гуревича, П. Ф. Дроздова, А. С. Залесова, Д. Р. Маиляна и др. [1–10, 14, 15].

Вопросы нелинейной работы железобетона с трещинами при силовых воздействиях пластин изучали Н. И. Карпенко, М. Д. Кутуев, Ж. Т. Тентиев, К. Темикеев и др. [11-13, 16, 17]. В этих работах изучались или аналитические нелинейные зависимости бетона и арматуры, или напряженно-деформированное состояние сечений при различных упрощающих положениях, не учитывая влияние разгрузки средней зоны сечения.

Исходя из вышеизложенного для апробации теоретических положений, в матрица внешней жесткости, вычисления ее элементов через единичные перемещения по определению напряженно-деформированного состояния сечения железобетонного элемента при чистом изгибе в стадии до образования трещин с учетом эффекта разгрузки средней зоны, обусловленного различной деформативностью бетона при растяжении и сжатии выполнен численный эксперимент с целью: проверить возможность раскрытия внутренней статической неопределимости напряженно-деформированного состояния сечения; определить деформированное состояние сечения в целом и его средней зоны: определить распределение нормальных напряжений по высоте сечения при различных уровнях воздействия изгибающего момента.

При выполнении эксперимента решались следующие задачи: исследовать качественно и количественно траекторию центров мгновенного поворота сечения, определить деформирование центра тяжести сжатой и растянутой граней сечения; исследовать характер распределения напряжений в сечении и его средней зоне, где волокна сначала сжимаются, а затем частично или полностью разгружаются с переходом в растяжение; выявить характер изменения положения центров общего поворота (нейтральной оси по деформациям); выявить положение нейтральной оси по напряжениям в процессе нагружения; выявить положение; выявить характер изменения нейтральной оси по напряжениям в процессе нагружения; определить значение изгибающего момента при трещинообразовании; выявить влияние на указанные факторы класса бетона и класса арматуры.Численный эксперимент выполнен для железобетонного элемента прямоугольного сечения с одиночной арматурой. Исследование проводилось при армировании сечения арматурой классов A-II и А-III и варьировании класса бетона от В10 до В60 и коэффициентов армирования от 0,0025 до 0,0125.

Численный эксперимент проводился по специальной программе по аналитическим зависимостям. Траектория центра мгновенного поворота сечения для класса бетона В12,5 и класса арматуры А-III показана на Рисунке 1. Выпуклость кривой направлена в сторону оси Х. В начале нагружения положение оси изменяется медленно, а затем более интенсивно. На Рисунке 2 показан график изменения деформаций на уровне центра тяжести сечения в зависимости от положения оси мгновенного поворота сечения. При увеличении изгибающего момента деформация вначале растет медленно, а затем приращение ее увеличивается, достигая в момент трещинообразования величины — 8,5∙10-6.

Зависимость изменения положения центра мгновенного поворота сечения от кривизны показана на Рисунке 3. При трещинообразовании кривизна составила 1,75 ∙ 10-4 рад. С увеличением кривизны смещения положение Центра мгновенного поворота замедляется.

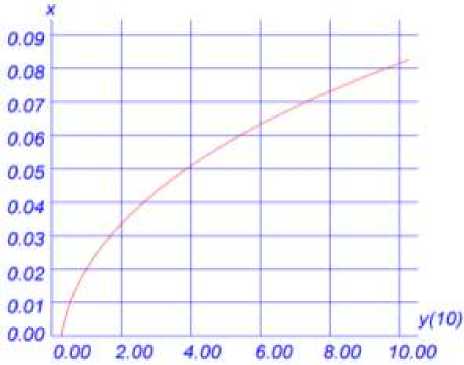
Рисунок 1. График траектории мгновенного       Рисунок 2. Деформация центра тяжести центра поворота

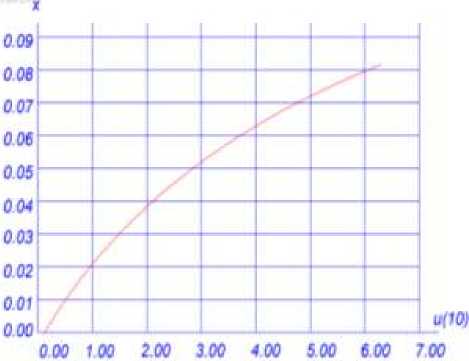
сечения от положения мгновенного центра

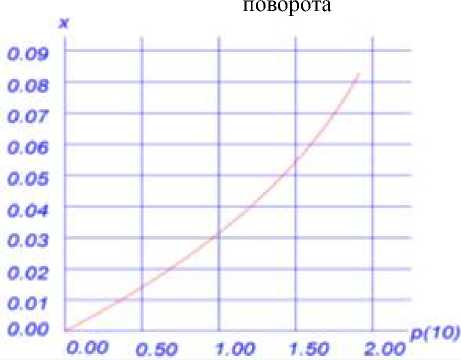
Рисунок 3. Зависимость кривизны от координат мгновенного центра поворота

График нейтральной оси по деформациям показан на Рисунке 4. Эта зависимость имеет слабо выраженную нелинейность. В момент перед образованием трещин перемещение оси по высоте сечения составило 0,04h. На Рисунке 5 показаны графики, для сопоставления, деформации центра тяжести сечения для классов бетона В12, B25, B40 и В60. С увеличением класса бетона, что характеризуется ростом значений и, положение центра мгновенного поворота. График зависимости траектории оси мгновенного поворота сечения от изгибающего момента показан на Рисунке 6.

На Рисунке 7 показаны графики напряжений в относительных напряжениях r/Rbtn для класса бетона В60 и класса арматуры А-I, а на Рисунке 8, то же для класса бетона В10. Из сопоставления графиков видно, напряжения сжатой грани бетонов более высокого класса бетона меньше, чем для бетонов низкого класса. Из сравнения графиков Рисунка 6 и 7 можно заметить, увеличение класса бетона и арматуры увеличивает длину траектории, но если с увеличением класса бетона увеличивается пологость, то с увеличением коэффициента армирования пологость уменьшается.

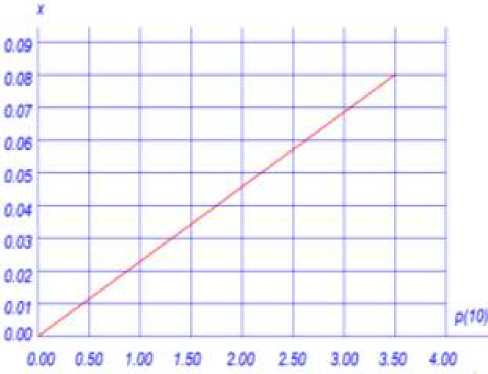
Рисунок 4. Зависимость между траекторией центра мгновенного поворота и положением нейтральной оси по напряжениям

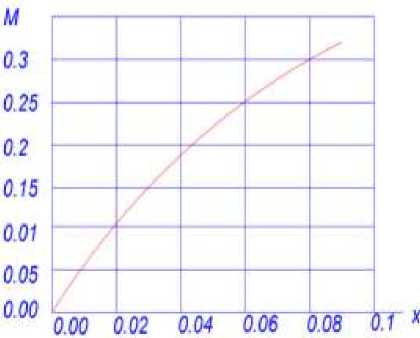
Рисунок 5. Зависимость между траекторией

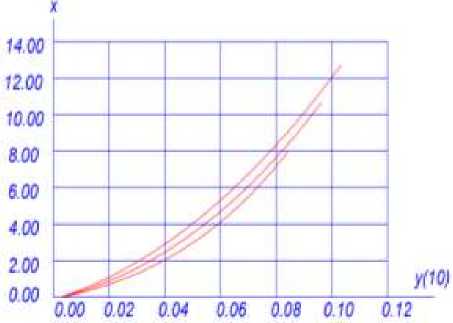
Рисунок 6. Влияние класса бетона на траекторию центра мгновенного поворота сечения

центра мгновенного поворота сечения от

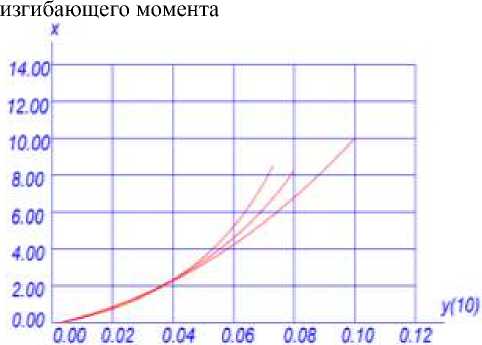
Рисунок 7. Влияние коеффицента армирования на траекторию центра мгновенного поворота сечения

На Рисунке 8 (B12,5; A-II, ц = 0,01) показаны графики распределения нормальных напряжений в сечении при напряжениях в растянутой грани сечения a_t = (0,25...1,0) Rbtn. Из графиков видно, с увеличением момента эпюра нормальных напряжений в растянутой и средней зоне заметно искривляется, а в сжатой грани эпюра почти линейная. На Рисунке 9 показано влияние на распределение нормальных напряжений класса бетона. Для бетонов более высокого класса напряжение в уровне центра мгновенного поворота сечения больше, чем для бетона более низкого класса.

В Таблице 1, 2 и 3 показано влияние на положение по высоте сечения центра мгновенного поворота. Для арматуры классов A-II и А-III положение центров мгновенного поворота при образовании трещин мало отличаются друг от друга.

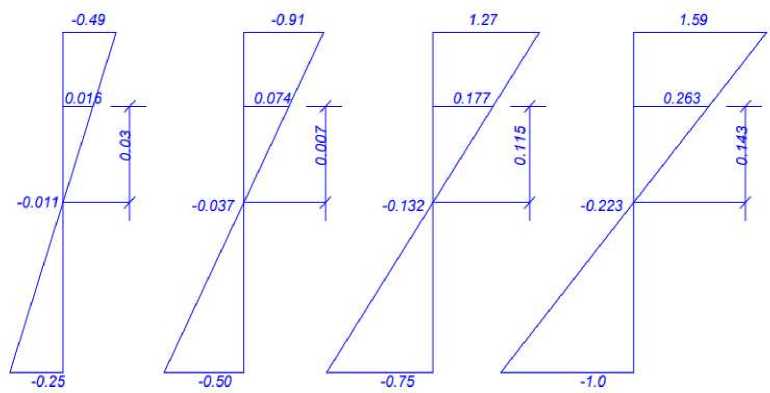
Рисунок 8. Распределение напряжений по высоте сечения при различных значениях величины изгибающего момента (д = 0,01; В12,5; А-II)

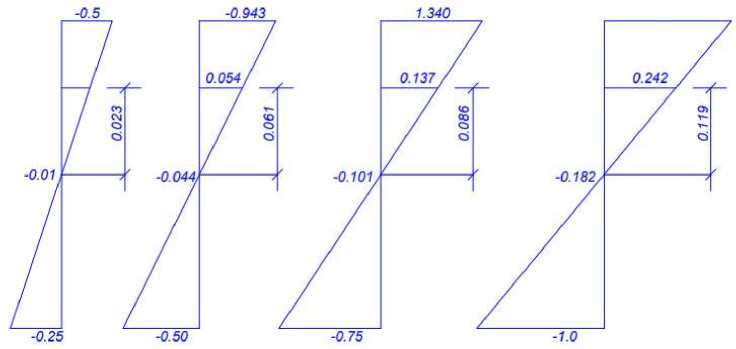
Рисунок 9. Распределение напряжений по высоте сечения при различных значениях величины изгибающего момента (д = 0,01; В40; А-II)

Таблица 1

(H t = 0,0025)

x/h	0,02	0,04	0,06	0,08
A – II	0,51	1,90	4,00	6,68
A - III	0,52	1,91	4,01	6,70
		(^ = 0,0075)		Таблица 2
x/h	0,02	0,04	0,06	0,08
A – II	0,61	2,25	4,72	7,87
A - III	0,60	2,23	4,66	7,78
		(щ = 0,0125)		Таблица 3
x/h	0,02	0,04	0,06	0,08
A – II	0,72	2,65	5,52	-
A - III	0,71	2,60	5,42	-

В Таблице 4 приведены значения относительных моментов трещинообразования для различных классов бетона и коэффициента армирования при арматуре классов A-II и А-ІІІ. Коэффициент армирования оказывает слабое, но более заметное, чем класс арматуры, влияние на образование трещин. Класс бетона В60 увеличивает момент трещинообразования более чем в два раза, по сравнению с классом В12,5.

Таблица 4

МОМЕНТ ТРЕЩИНООБРАЗОВАНИЯ ДЛЯ РАЗЛИЧНЫХ КЛАССОВ

БЕТОНА И КОЭФФИЦИЕНТА АРМИРОВАНИЯ

n t		0,0025	0,0075	0,0125
A=II	B12,5	0,238	0,242	0,246
	B40	0,497	0,505	0,509
	B60	0,592	0,599	0,604
A - III	B12,5	0,237	0,242	0,246
	B40	0,496	0,502	0,507
	B60	0,591	0,599	0,602

Выводы

Выполненный численный эксперимент качественно и количественно подтвердил теоретические разработки, которые позволяют раскрыть внутреннюю статическую неопределимость сечения и определить напряженно-деформированное состояние сечения, учитывающего зоны, обусловленный различной упруго эффект разгрузки средней пластической деформативностью при сжатии и растяжении и разработанный теоретический метод расчета позволяет определить момент образования трещины при чистом изгибе по рабочему состоянию, используя реальные диаграммы деформирования бетона при сжатии, растяжении и разгрузке.