Исследование напряженно-деформированного состояния соединения изделий из композиционных материалов

пряжений. Это позволяет значительно снизить радиальные растягивающие напряжения на границе “подкрепляющий элемент - листовая заготовка” при эксплуатационных нагрузках и сохранить, тем самым, клеевую прослойку. В работе [5] разработана математическая модель, определяющая зависимость конструктивных параметров процесса образования отверстий с подкрепленными стенками на деформированное состояние подкрепляющего элемента по внешнему контуру и на границе отверстия листовой анизотропной детали.

В работе [6] представлена конечно-элементная модель и методика расчетов для определения напряженного состояния по контуру механического точечного соединения с подкреплением в листовой детали из композиционных материалов для случая ее растяжения .

Целью данной работы является исследование напряженно-деформированного состояния по контуру соединения с подкреплением пластинки из КМ в случае действия силы Q, приложенной к болту, уставленному в отверстие втулки, и силы Р, приложенной к заготовке (рис. 2.). При этом вследствие неоднородности материала, малого относительного удлинения и упруго-вязких свойств полимерного связующего важными

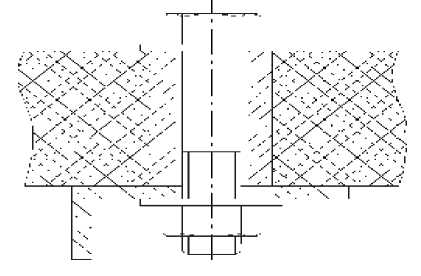
Рис. 1. Конструкция подкрепления стенок отверстий в листовой заготовке из КМ

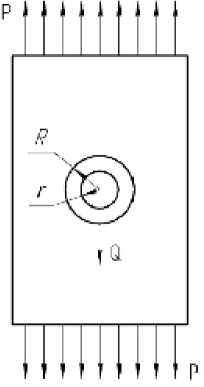
Рис. 2. Растяжения пластины с подкрепленным отверстием при действии сил Q и Р

являются определение критического радиального натяга по контуру отверстия с подкреплением и запаса прочности при эксплуатационных нагрузках.

Имеется ряд критериев прочности, позволяющих оценить предельное состояние для упругих ортотропных и изотропных материалов [1, 7]. Однако в этих критериях не учитываются такие особенности композитов, как различная прочность на растяжение и сжатие. В работе [7] предложен критерий прочности Дж. Марина, учитывающий эту особенность. Для плоского напряженного состояния в случае, когда главные оси анизотропии совпадают с осями главных напряжений, этот критерий имеет вид

^ ' + L g ₂ + L .^ + L ₃ g ₂ = L ₄ , (1) где L ■ — L ₄ - коэффициенты, определяемые из следующих соотношений:

L 1 = 2 — [ R сж 2 — R p . — T ; ₅₀( R сж 1 — — R p 1 — R сж 1 R p 1 / R p 2 + R p 2) ]/ T 45 0 ;

L 2 = R_C ж 1 — R p 1 ;

L ₃ = Rcж 1 R p 1

L 4 = R сж 1 R p 1 ;

U [ El ₊ "  Rg E 2

/ R p 2 — R p 2 ;

G

k — v_n( k + N )] ;

E 1

<7 2

= U -( k + N — v ,2 ); k=, E 2 ;

Rg

N =

^{2 ( k —} V 12 ^{) +} - ^El ;

G 12

_ ^{(1 — V} 12 ^V 21 ) g = E 2 + G 12

R _сж 1 ’ R _сж 2, Rp 1’ Rp 2 - прочность соответственно на сжатие и растяжение по главным осям; Т ₄₅ о - прочность на сдвиг; E 1 и E 2 - модули упругости материала листовой заготовки во взаимно-перпендикулярных направления; v ₁₂ и v ₂₁ коэффициенты Пуассона; G 12 - модуль сдвига; U_r - величина радиального перемещения; R-радиус отверстия в листовой заготовке.

Для определения прочностных характеристик, в соответствии с методикой [8, 9], проводились испытания на одноосное статическое растяжение образцов из углепластика марки КМУ-4Л и на смятие болтовых соединений пластин из этого материала по схеме (рис. 3). Для испытаний на статическое растяжение изготавливались: образцы прямоугольной формы длиной 250 мм и шириной 10 мм; на смятие прямоугольной формы длиной 150 мм и шириной 30мм. Диаметр крепежного элемента составлял 8,0мм на расстоянии от края образца 18 мм. Толщина образца составляла 4,0 мм. При статическом растяжении определяли прочностные характеристики по главным осям R р ₁ и R _{р 2} . Проведенные испытания болтовых соединений позволили получить удельные характеристики на смятие по главным осям R _сж 1 и R _{сж 2} . Решив совместно уравнения (1) и (2) относительно U _r определялось значение критического натяга для данного материала, которое составило 1,2%.

При испытании болтовых соединений также производилось варьирование направлением вырезки образцов, диаметром крепежного отверстия, отношением геометрических параметров

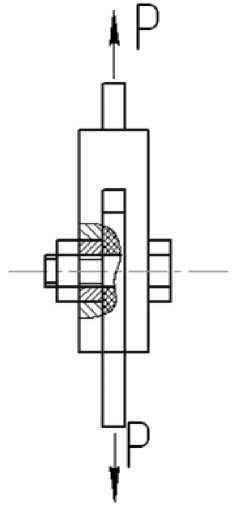
Рис. 3. Схема испытания на смятие болтовых соединений пластин

отверстия и образца. В результате обобщения экспериментальных данных по методике [7, 8] построены поверхности максимальных напряжений, соответствующих уровню разрушающей нагрузки. Они представляют собой трехмерные диаграммы зависимости номинальных напряжений от угла вырезки образца, а также от геометрических и конструктивных параметров соединения. По полученным результатам построена диаграмма анизотропии (рис. 4), по которой можно оценить напряженное состояние в образце при промежуточных значениях параметров и вычислить коэффициент запаса прочности. При указанных выше геометрических параметрах пластины и нагрузки Р по известным соотношениям [7] находили величину номинальных напряжений смятия. Восстановив перпендикуляр к плоскости d- 6 в направлении поверхности максимальных напряжений с учетом направления приложения нагрузки и диаметра крепежного элемента d, определялась точка, в которой нормаль пересекает поверхность А. Отложив на перпендикуляре отрезок ВС, величина которого равна а ^м , определялся коэффициент запаса прочности как отношение отрезков АВ к ВС.

Поверхности максимальных напряжений могут позволить решать не только задачу о нахождении коэффициента запаса прочности, но и обратные задачи:

• -    нахождение допустимых значений напряжений в пластине из КМ в зоне крепежного отверстия по известным коэффициенту запаса прочности, типоразмеру крепежного элемента и моменту предварительной затяжки;

• -    определение оптимальных параметров материала по уровню и направлению нагружения, параметрам крепежного элементам, конструктивным параметрам;

• -    оптимизация отдельных параметров крепежного элемента по уровню и направлению нагружения соединения;

• -    оптимизация конструктивных параметров соединения.

Определение напряженно-деформированного состояния по контуру соединения с подкреплением пластинки из КМ в случае действия сил Q и Р, выполнялось с помощью метода конечных элементов [10]. Для этого использовалась система MSC/NASTRAN [11]. Конечно-элементная модель включала в себя квадратную ортотропную пластинку размером 48 R, в центре которой располагается отверстие радиусом R. Втулка имела внутренний радиус г и внешний контур, определяемый функцией R + ur (ф) , где Ur (ф) — величина раздачи при запрессовке, зависящая от угловой координаты ф. Рассматривался случай симметрии механических свойств ортотропной пластинки, внешних нагрузок и формы запрессованной втулки относительно одной из плоскостей – XOZ, перпендикулярной плоскости пластинки. Поэтому конечно-элементная модель (рис. 5), строилась для половины пластинки с использованием соответствующих условий симметрии. Кроме того на сторонах втулки перпендикулярных силе Р задавались вынужденные перемещения, соответствующие силе Р. К половине внутренней поверхности втулки по косинусоидальному закону прикладывалось давление, соответствующее силе от болта Q.

Расчет напряженно-деформированного состояния по разработанной модели выполнялся в три этапа.

• 1.    Определялись напряжения и деформации в пластинке с вклеенной втулкой от действия внешних нагрузок. При этом элементы втулки и пластинки жестко связаны между собой. Монтажные деформации отсутствуют. Расчет проводился в линейной постановке.

• 2.    Определялись монтажные напряжения, появляющиеся в результате запрессовки втулки, с учетом контакта между втулкой и пластинкой. Для моделирования контакта между элементами втулки и пластинки вставлялись контактные конечные элементы. Расчеты проводились в нелинейной постановке.

• 3.    Результирующее решение получалось суммированием монтажных напряжений и деформаций с напряжениями и деформациями, обусловленными внешней нагрузкой.

Адекватность разработанной конечно-элементной модели проверялась путем сравнения результатов КЭ-расчетов с аналитическим решением для тестового случая. В качестве тестовой рассматривалась задача [12] определения радиального контактного напряжения в изотропной полосе, растягиваемой силой Р и в отверстие которой вложена шайба, нагруженная усилием Q. При этом задача рассматривалась в пределах малых упругих деформаций, диаметры отверстия и шайбы равны между собой, а трением по контактной поверхности пренебрегали. По условию задачи по концам полосы задавались растягивающие перемещения, таким образом, чтобы растягивающая сила Р в четырех случаях нагружения принимала значения: Р = 0/ 2 Q / 4 Q / 6 Q . Радиальные напряжения определялись из выражения

^ = - в r _F

2_ f _L П ^ г в*

P1   А.р .„

1,35— cos 6 +-- cos 6

Q J Q

,(3)

где F – площадь поперечного сечения полосы;

в =

в

^в ( 1 + ц ) + 1 - ц

. в = EX.

;; E

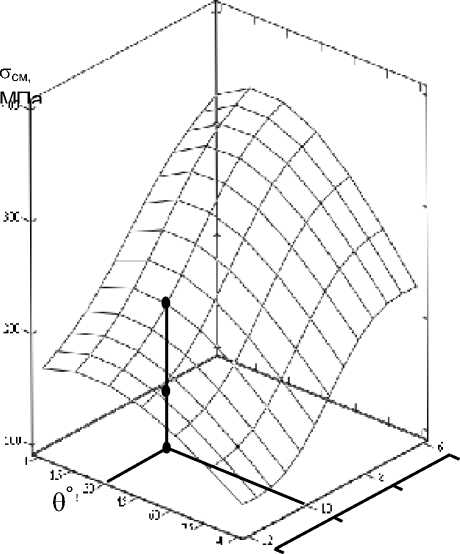
Рис. 4. Диаграмма анизотропии прочностных свойств болтового соединения

Рис. 5. Конечно-элементная модель пластинки с втулкой

E ₁ – модуль упругости материала шайбы; E – модуль упругости материала пластины; b – ширина полосы; r - радиус отверстия в пластине; Ц -коэффициент Пуассона материала пластины.

Результаты сравнения в характерных точках приведены на рис. 6. Анализ результатов КЭ-рас-четов и аналитического решения показал хорошее согласование результатов

Для исследования напряженно-деформированного состояния по контуру отверстия с подкреплением проводилось конечно-элементное

моделирование на пластинке размером 240 О 240 мм. Толщина пластинки составляла 1,0 мм. При этом наружный диаметр втулки был равен 5,0 мм, внутренний диаметр 3,0 мм. Пластинка находилась под действием силы от болта, установленного в отверстие втулки, равной 500 Н. Материал пластинки имел следующие характеристики: E₁=120000 МПа, E₂=8000 МПа, G ₁₂ =4000 МПа, х₁₂= 0,3, х ₂₁ =0,02 Материал втулки – алюминиевый сплав с характеристиками: E=70000 МПа, х=0,3. Заданные отклонения внешней поверхности втулки от круговой показано на рис. 6. Величина давления на стенки отверстия от болта вычислялась следующим образом:

Р (Ф) = <

—болт²- • cos( ф ), для Ф G п • R1 • t

0,

для Ф £

п п

2;2

пп

2;2

где Q _болт – сила, приложенная к болту; j - угол, откладываемый в плоскости пластинки; j=0 – направление действия силы, приложенной к болту.

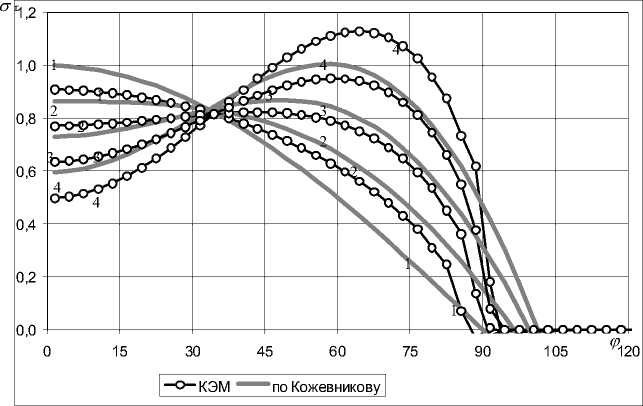
Рис. 6. Сравнение радиальных напряжений в контакте шайбы с пластинкой, полученных из соотношений [12] и из конечно-элементного расчета при закреплении пластинки с одной стороны:

1 – Р=0; 2 – Р=2Q; 3 – Р=4Q; 4 – Р=6Q;

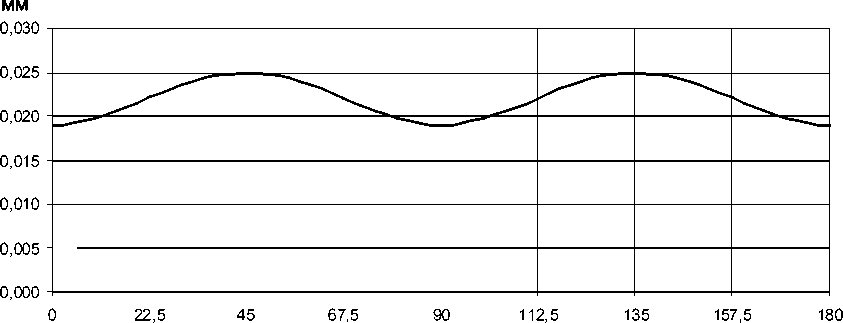
Рис. 7. Форма раздачи втулки при запрессовке

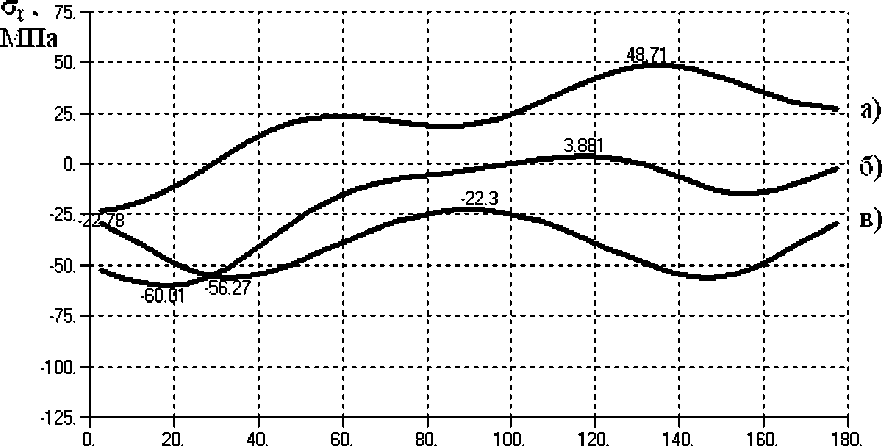
Рис. 8. Радиальные напряжения по контуру отверстия в пластинке при нагрузке от болта с силой 500Н и растяжении пластинки с напряжением 100 МПа: а – напряжения, обусловленные действием нагрузки;

б – напряжения, обусловленные действием нагрузки и запрессовкой;

в – напряжения от запрессовки

Проведенные исследования показали, что разработанный способ постановки втулки значительно снижает напряженное состояние по периметру отверстия с подкреплением (рис. 7) и увеличивает несущую способность силовой точки. Разработанная конечно-элементная модель и методика расчета показала хорошее согласование результатов с известными аналитическими решениями и позволяет с высокой точностью определять напряженное состояние по контуру силовой точки в анизотропных композиционных материалах.