Исследование напряженного состояния железнодорожного рельса трехэкспозиционным методом голографической фотоупругости

Одной из самых главных значимых задач теории упругости как для экспериментального, так и для аналитического и численного решений является исследование напряженно-деформированного состояния в местах контакта деталей.

Это объясняется следующими факторами: во-первых, нелинейностью задачи, связанной с изменением размеров контактной площадки в процессе нагружения, во-вторых, наличием высоких градиентов напряжений в зоне контакта.

В настоящее время при решении пространственных контактных задач достаточно широко применяются различные полуаналитические и численные методы [1, 2]. Недостатком всех численных методов является то, что они не позволяют гарантированно и доказательно оценить точность получаемого результата. При решении пространственных контактных задач методом КЭ очень трудно правильно задать соответствующие надстройки (метод решения, вид конечноэлементной сетки, тип и порядок конечного элемента и др.) при проведении расчетов. Использование метода конечных элементов также ограничивается ресурсами применяемых ЭВМ, что не позволяет построить корректную конечно-элементную сетку, например, для сложных пространственных конструкций. Такая практика приводит к ошибкам в результатах расчетов, которые проявляются только при эксплуатации, что может привести к тяжелым последствиям.

Поэтому проведение экспериментальных исследований для подтверждения правильности результатов решения пространственных контактных задач численными методами необходимо.

В механике деформируемого тела основное развитие получили два экспериментальных метода - метод фотоупругости и метод интерферометрии. Метод фотоупругости с использованием объемных составных моделей [3, 4] имеет ряд достоинств, таких как возможность полного исследования пространственного напряженного состояния на одной модели при различных нагрузках. С помощью метода фотоупругости можно получить интерференционную картину изохром, т. е. изолиний с постоянной разностью главных напряжений (с 1 - g₂). Недостатком данного метода является то, что если основная часть объемной модели изготовлена из полимера (оргстекло), обладающего некоторой оптической чувствительностью, то по обычной схеме невозможно определить направления квазиглавных осей во вклейке. Измеряется лишь с погрешностью 2-3 % оптическая разность хода методом интерференционных полос.

С помощью метода интерферометрии можно получить интерференционную картину изо-пахик, т. е. изолиний с постоянной суммой главных напряжений (g , + g₂). Используя информацию, которую содержат интерференционные картины изоклин и изопахик, можно легко получить раздельные значения главных напряжений при решении плоских задач, но для разделения напряжений в пространственных задачах этой информации недостаточно.

Метод голографической фотоупругости [5] имеет большие возможности при исследовании объемного напряженного состояния моделей реальных объектов, так как объединяет в себе возможности как метода фотоупругости, так и метода интерферометрии. Недостатком этого метода является то, что при исследовании модели в классическом интерферометре можно получить интерференционные картины, промодулированные несколькими семействами интерференционных полос (изоклин, изопахик и изодром). Если расстояния между этими се- – 324 –

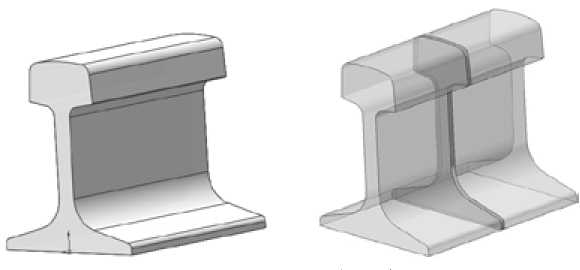
а – модель из блочного стекла б – модель со специальной пластинкой

Рис. 1. Объемная модель рельса

Fig. 1. Volume model of a rail

мействами достаточно велики и они практически ортогональны, то расшифровка такой интерференционной картины не составит труда. Но в большинстве случаев различные семейства интерференционных полос практически параллельны друг другу и качественная расшифровка таких интерферограмм практически невозможна.

На основе методов голографической фотоупругости и фотоупругости нами был разработан метод трех экспозиций, позволяющий разделить интерференционные картины изоклин, изопахик и изодром (изолиний постоянной разности хода). На основе данных, которые содержат три семейства интерференционных полос, разработана методика разделения напряжений пространственных задач теории упругости.

Применим разработанный метод трех экспозиций для исследования напряженного состояния при контакте колеса и рельса. Для этого необходимо изготовить три объемные модели рельса. Одна модель выполнена из блочного стекла (рис. 1 а ). Основная часть двух других рельс изготовлена из оргстекла, а в центральную часть вклеивается тонкая пластинка из оптически чувствительных материалов (рис. 1 б ). Первый цилиндр имеет вклейку из эпоксидной смолы, второй – из поликарбоната. Оптически чувствительные материалы вклеек подбирались так, чтобы их упругие постоянные были одинаковыми, а оптически постоянные С ₁ и С ₂ выполняли следующее условие:

С 1 _≠ С 2

с‘ с2 ’ где С1 и С2 - оптические постоянные материала на основе эпоксидной смолы; С‘ и С‘ - оптические постоянные поликарбоната.

Таким требованиям отвечают материал на основе эпоксидной смолы ЭД-6М и поликарбонат.

В классических голографических интерферометрах с наклонными опорными пучками используют двухэкспозиционный метод [4], с помощью которого можно получать интерференционные картины изохром, т. е. изолиний постоянной разности главных напряжений (g1 - g2); изопахик - суммы главных напряжений (о1 + о2), а также совмещенные картины – 325 – изохром и изопахик, изохром и изодром, т. е. изолиний постоянной абсолютной разности хода Si и S2.

Для получения отдельной картины изодром нами был предложен трехэкспозиционный метод голографической фотоупругости. Этот метод основан на исключении картины изодром путем наложения друг на друга интерференционной картины изодром с целыми порядками полос. Следовательно, на интерференционной картине с целыми порядками темные полосы соответствуют нулевой интенсивности света I = 0, а в этих же точках на интерференционной картине с половинными порядками полос I = I max и наоборот. Таким образом, при совмещении двух интерференционных полос получается сплошное серое поле, на котором отчетливо видна интерференционная картина изодром.

Для получения изодром трехэкспозиционным методом был разработан универсальный интерферометр [6].

Последовательность трехэкспозиционного метода получения изодром

Первая экспозиция - модель находится в ненагруженном состоянии. Главные оси поляроидов в опорном и предметном пучках универсального интерферометра установлены вертикально, т. е. из поляризованного по кругу излучения получается плоскополяризованное излучение в вертикальной плоскости.

Вторая экспозиция - модель нагружается соответствующей силой. Главные оси поляроидов в опорном и предметном пучках остаются вертикальными.

При первых двух экспозициях получается совместная картина изохром (изолиний разности главных напряжений (G 1 ^- 0 2 )) ^{половинного} порядка и изодром.

Третья экспозиция - модель остается нагруженной той же силой. Поляризация света в предметном пучке остается вертикальной, а в опорном пучке главная ось поляроида разворачивается на 90°, т. е. устанавливается горизонтально, и изохромам соответствуют целые порядки полос.

Другими словами, при третьей экспозиции на картину изохром темного поля накладывается картина изохром светлого поля и получается серый фон, на котором отчетливо видны изодромы (рис. 2).

Последовательность раздельного получения главных напряжений исследуемой модели рельса методом голографической фотоупругости с использованием двух объемных моделей с вклейками из эпоксидной смолы и поликарбоната: модель первой модели рельса с вклейкой из

Рис. 2. Интерференционная картина изодром в объемной модели рельса, полученная методом трех экспозиций

Fig. 2. Interferential isodromic picture in volume model of a rail, received by method of three expositions материала на основе эпоксидной смолы помещается в рабочее поле универсального интерферометра и фотографируется голограмма, содержащая интегральные интерференционные картины. Абсолютная разность хода, накапливаемая в первой объемной составной модели рельса, описывается выражением

7 о о

^A   J [С 1 ^{0 1} + С 2 ^{( о} 2 + ^о 3 )] ds +

s

+ [Ci Oi + С2 (о2 +03)] d + j[С0О1 + С0(о2 + 03)] ds, si+ d где 51 - путь луча света в модели до вклейки; 5 - путь луча света по всей модели; d - толщина вклейки из оптически чувствительного материала; С1 и С2 - оптические постоянные материала основной части модели; Сj и С2 - оптические постоянные материала вклейки; Gj, g2, g3 -главные напряжения.

Как видно из выражения (2), абсолютная разность хода, накапливаемая в основной части составной модели, вносит достаточную погрешность. Для исключения этой ошибки предлагается определить величину абсолютной разности хода для модели, полностью изготовленной из блочного органического стекла. Тогда абсолютная разность хода, накапливаемая в сплошной модели цилиндра, описывается выражением

• - 0 = j [с 1 о 1 + C 0 ( о ₂ + о ₃ )] ds.                                         (3)

Следовательно, абсолютная разность хода, накапливаемая во вклейке, будет определяться выражением

А 1=-¹— = (С - С 0 ) О 1 + (С 2 - С 20 )( О 2 + О 3 ) .                    (4)

d

Получить дополнительную информацию можно, используя различные оптические свойства материалов, из которых изготавливаются вклейки, т. е. можно получить еще одно уравнение абсолютной разности хода, аналогичное уравнению (4), для составной модели с вклейкой из другого оптически чувствительного материала. В этом случае материалы для вклеек подбираются так, чтобы их оптические постоянные выполняли условие (1).

Поместив вторую модель цилиндра с вклейкой из поликарбоната в предметный пучок интерферометра, получаем уравнение абсолютной разности хода А2

Л 2 = J [C « „ i + C⁰⁰ ( , 2 + „ )] ds + [C ‘ „ + C 2 ( „ 2 + . Я d + 0

_s                                                                                               ⁽⁵⁾

+ J [C 1 „ 1 + C ₂ ⁰ ( „ ₂ +„ ₃ )] ds. s l + d

Вычитая из полученной величины абсолютную разность хода, накапливаемую в сплошной модели рельса (3), получаем величину абсолютной разности хода, накапливаемую во вклейке из поликарбоната:

^А 2 = ^--^ = (С 1 - С) . + (С 2 - С 20 ) ( . 2 + . 3 ) .                    (6)

d

Решая совместно систему уравнений (4) и (6), получаем величину первого квазиглавного напряжения

. =------ А’ ⁽С ‘— С ^- ) -^А 2 ⁽С ² - С 2 ) -----0- .                     (7)

⁽ С 1 ^- С 1 ) ⁽ С 2 ^- С 2 ) - ⁽ С ‘ ^- С 1 ⁾⁽ С 2 ^- С 2 )

Абсолютные разности хода Δ ₁ и Δ ₂ определялись с использованием интерференционных картин изодром, полученных методом трех экспозиций.

Величина абсолютной разности хода связана с порядком изодромы следующим выраже нием:

Δ = n λ,

где n – порядок изодромы.

Следовательно, абсолютная разность хода Δ ₁ в модели с вклейкой из полимера на основе эпоксидной смолы определяется уравнением

(« 1 - « 0 )х ' =        .

где n 1 - порядок изодромы в модели с вклейкой из полимера на основе эпоксидной смолы; n о -порядок изодромы в сплошной модели.

Абсолютная разность хода Δ′2 в модели с вклейкой из полимера на основе эпоксидной смолы определяется уравнением д’ = <112 -n0)\

2 d ’ где n2 - порядок изодромы в модели с вклейкой из поликарбоната.

Для определения второго главного напряжения требуется дополнительная информация, которую можно получить при расшифровке интерференционной картины изохром, которая регистрируется в голографическом универсальном интерферометре и содержит информацию об оптической разности хода:

6 = С „ ( = 1 -а 2 ) ,                                                        ⁽¹¹⁾

где C σ – оптический коэффициент по напряжениям.

Непосредственно с использованием картины изохром оптическая разность хода определя ла ется по формуле

δ = n λ,

где n – порядок изохромы.

Тогда из уравнения (11) определяется второе квазиглавное напряжение:

=   = А.                                                 (13)

С σ

Теперь, зная величины двух квазиглавных напряжений а и о2, из уравнений (4) и (6) можно определить третье квазиглавное напряжение:

А‘ _п - (С 1 — С 0 )

( С 2 - С 0 )   ² ( С 2 - С 0 ) ■

Точность раздельного определения компонентов тензора напряжений при взаимодействии рельса и колеса по предлагаемой методике проверялась сравнением экспериментальных результатов с аналитическим решением [7] и результатами решения тестовой задачи – «Исследование напряженного состояния при контакте двух цилиндров со скрещивающимися осями».

Результаты экспериментального исследования трехэкспозиционным методом голографической фотоупругости напряженного состояния рельса в сравнении с теоретическим решением и результатами тестовой задачи приведены на рис. 3, 4.

Расхождение экспериментальных и теоретических результатов составило менее 5 %, что говорит о высокой точности предложенной методики разделения напряжений при решении пространственных задач трехэкспозиционным методом голографической фотоупругости.

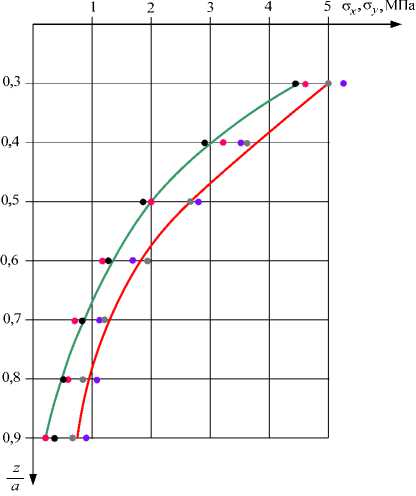
Рис. 3. Графики теоретических и экспериментальных значений напряжений a x : - - теоретические значения напряжений σ x ; • – экспериментальные значения напряжений σ x для модели рельса; • – экспериментальные значения напряжений σ x для модели цилиндра; - – теоретические значения напряжений σ y ; • – экспериментальные значения напряжений σ y для модели рельса; • – экспериментальные значения напряжений σ y для модели цилиндра

Fig. 3. Diagrams of theoretical and experimental values of the a _x stress: - - theoretical values of the a _x stress; • – experimental values of the σ _x stress for rail model; • – experimental values of the σ _x stress for cylinder model; - – theoretical values of the σ _y stress; • – experimental values of the σ _y stress for rail model; • – experimental values of the σ _y stress for cylinder model

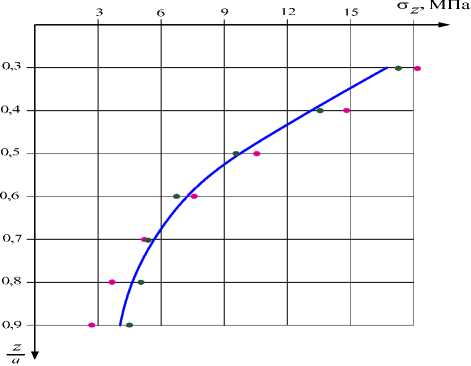
Рис. 4. Графики теоретических и экспериментальных значений напряжений σ _z : - – теоретические значения напряжений σ _z ; • – экспериментальные значения напряжений σ _z для модели рельса; • – экспериментальные значения напряжений σ z для модели цилиндра

Fig. 4. Diagrams of theoretical and experimental values of the σ _z stress: - – theoretical values of the σ _z stress; • – experimental values of the σ _z stress for rail model; • – experimental values of the σ _z stress for cylinder model