Исследование немарковской динамики двух взаимодействующих кубитов на основе численного решения нелинейного стохастического уравнения Шрёдингера
Автор: Павельев Андрей Владимирович, Семин Виталий Владимирович
Журнал: Компьютерная оптика @computer-optics
Рубрика: Дифракционная оптика, оптические технологии
Статья в выпуске: 2 т.43, 2019 года.
Бесплатный доступ
В работе исследуется немарковская динамика системы, состоящей из двух взаимодействующих кубитов. На основе идей стохастического исчисления выведено и обобщено на немарковский случай нелинейное стохастическое уравнение Шрёдингера. Стохастическое уравнение решается путём прямого компьютерного моделирования. На основе решения строятся различные динамические характеристики рассматриваемой системы.
Открытая квантовая система, нелинейное уравнение шрёдингера, диполь-дипольное взаимодействие, кубит
Короткий адрес: https://sciup.org/140243276
IDR: 140243276 | DOI: 10.18287/2412-6179-2019-43-2-168-173
Текст научной статьи Исследование немарковской динамики двух взаимодействующих кубитов на основе численного решения нелинейного стохастического уравнения Шрёдингера
Моделирование динамики связанных кубитов имеет большое значение для задач квантовых вычислений и квантового компьютинга [1]. В традиционном подходе к математическому описанию систем кубитов, представленных в классических монографиях [1, 2], не учитывается деструктивное влияние окружения на динамику запутанных состояний, которые играют первостепенную роль при построении любого квантового алгоритма. Ясно, что декогерен-ция, вызванная взаимодействием кубитов с внешним окружением, приводит к разрушению запутанных состояний [3] и не может игнорироваться.
Для описания динамики открытых квантовых систем (ОКС) наиболее часто используется подход, основанный на решении операторно-кинетического уравнения для матрицы плотности (англ. master equation ). Базовым допущением при выводе операторнокинетического уравнения является марковское приближение [3], которое характеризуется пренебрежением всеми эффектами памяти, связанными с динамикой окружения.
В ряде недавних экспериментальных работ было показано проявление немарковских эффектов в динамике квантовых систем [4–9]. Также было показано, что немарковские эффекты могут оказывать значительное влияние на динамику открытой квантовой системы [10, 11]. В связи с этим в последнее время прилагаются значительные усилия для обобщения марковского кинетического уравнения на немарковский случай [12, 13].
Однако попытки обобщить операторно-кинетическое уравнение на случай немарковской динамики не приводят к особым успехам [12, 13]. Основные трудности связаны с тем, что на сегодняшний день общая форма немарковского кинетического уравнения, гарантирующая сохранение положительной определенности матрицы плотности, неизвестна. Более того, имеются примеры, когда формально построен-
ное немарковское кинетическое уравнение приводит к совершенно нефизическим результатам [3].
В работе [14] А. Баркелли предлагает метод непротиворечивого описания динамики ОКС с учётом немарковских эффектов на основе стохастического уравнения Шрёдингера (СУШ). Данный подход, основанный на замене марковского белого шума на более общий немарковский процесс, гарантированно приводит к физически корректным свойствам оператора плотности.
В данной работе мы предлагаем описание немарковской релаксации двух диполь-дипольно взаимодействующих кубитов на основе нелинейного стохастического уравнения Шрёдингера. С помощью прямого численного моделирования анализируется динамика возбуждения различных квантовых состояний системы.
1. Нелинейное стохастическое уравнение Шрёдингера для системы из двух кубитов
В данной работе изучается система двух диполь-дипольно взаимодействующих кубитов в двух независимых термостатах. Марковское операторнокинетическое уравнение для матрицы плотности при нулевой температуре термостатов, полученное в работе [15], имеет следующую форму:
dp dt
= -1 Q[G+G2 + G+G, , p]-
— 2 Yo (G+Gip
- 2g, pG, + pG, G, )-
— 2 Yo (g2G2p
- 2G2pG2 + pG2G2 ),
где g + - понижающие и повышающие операторы для i -го кубита, Q - константа диполь-дипольного взаимодействия, у 0 - скорость релаксации. Квадратными скобками обозначен коммутатор двух операторов.
В результате процедуры распутывания (англ. unravelling ) [16] из данного операторно-кинетического
уравнения (1) можно вывести стохастическое уравнение Шрёдингера, которое будет эквивалентно последнему в смысле стохастического усреднения по ансамблю квантовых траекторий р = E (I vXv l).
Ранее в нашей работе [17] в результате процесса распутывания уравнения (1) было получено линейное стохастическое уравнение Шрёдингера для волновой функции. Его можно записать в следующем виде:
d| у) = A\ v) d t + B |V d W1 + C | y) d W 2 ,
A = - I П ( о + О2 + o + O 1 ) - 2 Y o ( 0 + 0 1 +0 + ^ 2 ) ,
в = i TYo" c , с = i TYo" 0 2 .
Для обобщения линейного СУШ (1) на немарковский случай в статье [14] было предложено заменить винеровские процессы d W i на процессы более общего вида. Примером такого процесса является процесс Орнштейна –Уленбека:
dX i = - k i X i dt + d W i ,
где k i – неотрицательные постоянные, отвечающие за характерное время скоррелированности с i- м термостатом. В результате формальной подстановки d W i ^ dX i получаем следующее выражение для кет-вектора:
d| y) = A| v) d t - k i X 1 B| v) d t - k 2 X 2 C | y) d t + + B | y) d W1 + C | y) d W 2.
Однако полученное уравнение (4) не сохраняет нормировку волнового вектора в среднем, что необходимо для физической интерпретации членов уравнения [16]. Для сохранения нормировки в среднем необходимо потребовать, чтобы величина | у) была мартингалом, то есть:
E (v|v) = 1, (5)
где E – усреднение по ансамблю стохастических реализаций. Из этого условия следует, что стохастическое уравнение для величины (v l v) должно содержать только шумовую часть.
Использование правила дифференцирования Ито:
d (у | у) = d (VI ■ I v) + (VI ■ d I v) + d (V | • d | V> позволяет получить СУШ следующего вида:
d (y|y) = «V| A t + A V)- k i X 1 (v| B t + B | V-
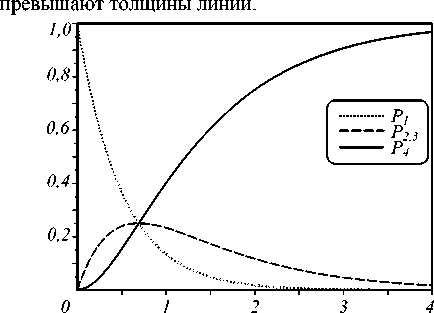
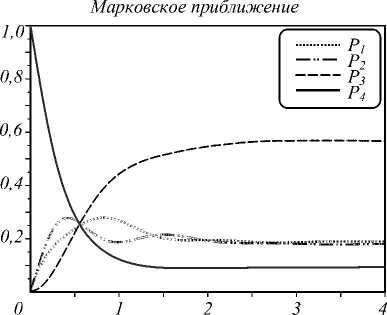
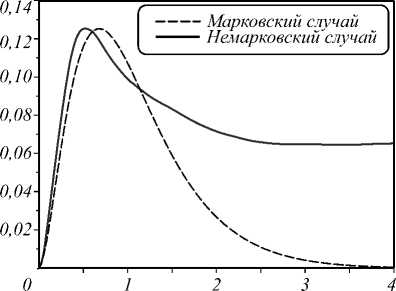
-k2X2 (v ICt + CIV) + + (v|Bt+ B|V)dW1+(v|Ct+ C|v)dW2. При выводе была использована таблица Ито: dwi ■ dWj=8j, dt ■ dt = 0, dt ■ dWi = 0.(8) Для выполнения свойства мартингальности член в выражении (7) при dt должен быть равен нулю. Это условие будет выполнено, если провести следующую замену в уравнении (4): A ^ A - k1X1Bt - k2X2Ct. (9) Окончательно уравнение, сохраняющее норму, имеет вид: d| v) = ( A - ki X1 (B + + B)-k2 X2(C + + C ))|v> dt + +B| v) dW + C |v) d W2. Решение данного уравнения является мартингалом, т.е. сохраняет нормировку в среднем. Хорошо видно, что при k1 = k2 =0 уравнение (10) переходит в марковское уравнение (2). Однако стохастические реализации решения обладают большой дисперсией, что приводит к тому, что для получения адекватного результата нужно смоделировать неоправданно много траекторий. Традиционный путь преодоления данного недостатка состоит в выводе нелинейного уравнения для нормированного волнового вектора: I "^^ = "/rTT = lv>llvir1, (11) V\v|v) которое эквивалентно исходному уравнению в слабом вероятностном смысле (другими словами, средние, вычисленные с помощью решения одного и второго уравнения, совпадают). Дифференцируя выражение для обратной нормы с использованием леммы Ито [18]: IVT1' 1 и заменяя волновую функцию в обкладках матричных элементов на нормированную волновую функцию, получаем: d||v||-1 = = 31ЫГ1(^ |B t + B| V )2+^ |Cf+ C| V )2) dt - (13) - 2| Ivll-1G Используя стохастическое исчисление Ито с одновременной заменой вероятностной меры процессов по теореме Гирсанова [18], можно получить нелинейное СУШ, которое гарантированно сохраняет норму волнового вектора в любой момент времени. Из уравнения (10) и уравнения (13) получаем замкнутое уравнение для нормированной волновой функции: d| V/) = ( A - k1 X1 (вt+ B)- k2X2 (Ct+ C) + +2 в (tV |bt+ b\tV)+2 с (V |Ct+ C| <й) - - 8 в ^ |Bt+ b\tV )2- 8 с ^ |ct+ с| V )2 +f C - 2 (tV |Ct+ C| tVW )d W2. В вышеприведённом уравнении новые шумы Wi определяются следующим образом: d Wi = dW + (/ Bf + B| / ), d W2 = d W2 + (/ |C t + C |/), dX1 =- k1 X1d t + dW +^ |B t + B| / )d t, (15) dX2 =- k2 X2d t + d W2 + (1/ |Cf+ C |/ )d t. Из выражений видно, что шумы также зависят от состояния системы. Полученное уравнение обладает рядом преимуществ: гарантирует полную положительность оператора плотности p = B(|\j/><14/1), сохраняет нормировку волновой функции в любой момент времени по построению, обладает меньшей дисперсией по сравнению с линейным уравнением (2). Уравнение (14) является стартовой точкой для проведения компьютерного моделирования. Имея N его решений (стохастических траекторий), можно получить среднее значение произвольного оператора M следующим образом: 1N (M=n E^-M Ы Например, вероятность обнаружить систему в состоянии, при котором оба кубита находятся на верхнем энергетическом уровне, можно найти как: N P=NE <-i g+Gj g+g2 При этом среднеквадратичное отклонение находится по формуле: ставлены на рис. 1 и 2 соответственно. Среднеквадратичные отклонения, найденные по формуле (18), не Рис. 1. Вероятность обнаружить систему в конкретном состоянии P от безразмерного времени γ0 t. Рис. 2. Вероятность обнаружить систему в конкретном состоянии P от безразмерного времени γ0 t. Немарковское приближение N< N E^M l,/-) —I EC^^-M l'/-) i=1 V -=1 . N (N -1) 2. Результаты моделирования Полученное выше нелинейное стохастическое уравнение Шрёдингера (14) записано для четырёхкомпонентного вектора | \Y . Квадрат модуля каждой компоненты соответствует вероятности обнаружить систему в одном из следующих состояний: оба кубита находятся на возбужденном энергетическом уровне (P1), один из кубитов находится в возбужденном состоянии (P2,3) или оба кубита – в основном состоянии (P4). Численное решение уравнения (14) проводилось с помощью явного метода Эйлера [19] со следующими значениями параметров: | /й (0)) = (1;0;0;0), У 0 = 1, (19) П = 2,3, к1 = 0,8, к2 = 1,6. Результаты усреднения по 100000 траекторий для марковской (k1,2 =0) и немарковской динамики пред- Из приведённых рисунков видно, что учёт немар-ковости снимает вырождение состояния, когда один из кубитов находится на верхнем энергетическом уровне. Кроме того, смещаются вероятности найти систему в одном из состояний в стационарном режиме. Учёт немарковского окружения также приводит к появлению осцилляций вероятностей, связанных с перекачкой энергии из одного кубита в другой. Вероятность обнаружить систему в симметричном перепутанном состоянии определяется следующим образом [20]: 1N Ps =^E^-lsXsl ^Y N i=1 1T где5 =Y/i(0;i;i;0). Зависимость вероятности обнаружить симметричное перепутанное состояние от безразмерного времени Y01 изображена на рис. 3 для марковского и немарковского случая соответственно. Из рис. 3 видно, что учёт немарковской релаксации приводит также к изменению вероятности найти систему в перепутанном состоянии в стационарном режиме. В марковском случае эта вероятность экспоненциально спадает к нулю с течением времени. Рис. 3. Зависимость вероятности обнаружить систему в симметричном перепутанном состоянии Ps от безразмерного времени γ0 t в различных приближениях Заключение Использование нелинейного стохастического уравнения Шрёдингера позволяет моделировать динамику системы кубитов как в марковском, так и в немарковском приближениях, и при этом обладает рядом преимуществ по сравнению с другими методами: гарантированность полной положительности матрицы плотности (характерно в принципе для подходов, основанных на СУШ) и сохранение нормы волнового вектора, что является ключевой особенностью нелинейного стохастического уравнения Шрёдингера. В данной работе получено нелинейное стохастическое уравнение Шрёдингера для немарковской релаксации системы из двух диполь-дипольно взаимо-действущих кубитов. Показано, что немарковость оказывает существенное влияние на динамику системы, в том числе на вероятность возбуждения перепутанных состояний, что может быть использовано как ресурс в квантовой информатике и квантовых системах связи. Данная работа была выполнена при поддержке Российского фонда фундаментальных исследований (грант № 18-32-00249).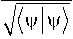
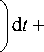
Список литературы Исследование немарковской динамики двух взаимодействующих кубитов на основе численного решения нелинейного стохастического уравнения Шрёдингера
- Nielsen, M.A. Quantum computation and quantum information/M.A. Nielsen, I.L. Chuang. -Cambridge: Cambridge University Press, 2000. -702 p. -ISBN: 978-0-521-63503-5.
- Баллаж, Ф. Квантовые вычисления и связь. Инженерный подход: пер. с англ./Ш. Имре, Ф. Баллаж. -М.: Физматлит. -2008. -319 c.
- Петруччионе, Ф. Теория открытых квантовых систем: пер. с англ./Х.-П. Бройер, Ф. Петруччионе; под ред. Ю.И. Богданова. -Ижевск: Регулярная и хаотическая динамика, 2010. -824 c.
- Liu, B.-H. Experimental control of the transition from Markovian to non-Markovian dynamics of open quantum systems/B.-H. Liu, L. Li, Y. Huang, C.F. Li//Nature Physics. -2011. -Vol. 7. -P. 931-934.
- Parkdag, S.H. Intraband relaxation time effects on non-Markovian gain with many-body effects and comparison with experiment/S.H. Parkdag, S.L. Chuang, J. Minch, D. Ahn//Semiconductor Science and Technology. -2000. -Vol. 15, Issue 2. -P. 203-208.
- Xu, J.-S. Experimental investigation of the non-Markovian dynamics of classical and quantum correlations/J.-S. Xu, C.F. Li, C.J. Zhang, X.Y. Xu, Y.S. Zhang, G.C. Guo//Physical Review A. -2010. -Vol. 82. -042328.
- Orieux, A. Experimental on-demand recovery of entanglement by local operations within non-Markovian dynamics/A. Orieux, A. D'Arrigo, G. Ferranti, R.L. Franco, G. Benenti, E. Paladino, G. Falci, F. Sciarrino, P. Mataloni//Scientific Reports. -2015. -Vol. 5. -8575.
- Bernardes, N.K. Experimental observation of weak non-Markovianity/N.K. Bernardes, A. Cuevas, A. Orieux, C.H. Monken, P. Mataloni, F. Sciarrino, M.F. Santos//Scientific Reports. -2015. -Vol. 5. -17520.
- Xu, J.-S. Experimental recovery of quantum correlations in absence of system-environment back-action/J.-S. Xu, K. Sun, C.-F. Li, X.-Y. Xu, G.-C. Guo, E. Andersson, R.L. Franco, G. Compagno//Nature Communications. -2013. -Vol. 4. -2851.
- Rotter, I. A review of progress in the physics of open quantum systems: theory and experiment/I. Rotter, J.P. Bird//Reports on Progress in Physics. -2015. -Vol. 7, Issue 11. -114001.
- de Vega, I. Dynamics of non-Markovian open quantum systems/I. de Vega, D. Alonso//Reviews of Modern Physics. -2017. -Vol. 89. -015001.
- Barnett, S.M. Hazards of reservoir memory/S.M. Barnett, S. Stenholm//Physical Review A. -2001. -Vol. 64. -033808.
- Campbell, S. Critical assessment of two-qubit post-Markovian master equations/S. Campell, A. Smirne, L. Mazzola, N.L. Gullo, B. Vacchini, T. Busch, M. Paternostro//Physical Review A. -2012. -Vol. 85. -032120.
- Barchielli, A. Stochastic Schrödinger equations with coloured noise/A. Barchielli, C. Pellegrini, F. Petruccione//Europhysics Letters. -2010. -Vol. 91, Issue 2. -24001.
- Mikhailov, A.V. The Fokker-Planck equation for relaxation of a system of two dipole-dipole interacting atoms/V.A. Mikhailov, N.V. Troshkin, A.M. Trunin//Proceedings of the SPIE. -2015. -Vol. 9917. -991732.
- Barchielli, A. Quantum trajectories and measurements in continuous time: The diffusive case/A. Barchielli, M. Gregoratti. -Berlin, Heidelberg: Springer-Verlag, 2009. -325 p. -ISBN: 978-3-642-01297-6.
- Semin, V. Simulation of non-Markovian dynamics of dipole-dipole interacting atoms/V. Semin, A. Pavelev//Journal of Physics: Conference Series. -2019. -Vol. 1096. -012169. -
- DOI: 10.1088/1742-6596/1096/1/012169
- Оксендаль, Б. Стохастические дифференциальные уравнения. Введение в теорию и приложения/Б. Оксендаль. -М.: Мир, 2003. -408 с.
- Platen, E. Numerical solution of stochastic differential equations with jumps in finance/E. Platen, N. Bruti-Liberati. -Berlin: Springer, 2010. -869 p.
- Баргатин, И.В. Запутанные квантовые состояния атомных систем/И.В. Баргатин, Б.А. Гришанин, В.А. Задков//Успехи физических наук. -2001. -Вып. 171. -С. 625-647.


