Исследование необходимости учета насыщенных параметров при моделировании генератора на основе данных СВИ

Моделирование синхронных машин необходимо для выбора параметров первичного оборудования, расчета уставок релейной защиты и проти-воаварийной автоматики.

Традиционно синхронная машина моделируется с учетом системы уравнений Парка – Горева [1]. При этом существует множество различных версий моделей в зависимости от принимаемых допущений. Пакеты программ Rustab и Power Systems Transients часто используются в России для расчета режимов в действующих значениях, они представляют генератор как электродвижущую силу (ЭДС) и сопротивление. В вышеперечисленных программных пакетах имеется возможность ввода характеристик холостого хода (ХХХ) для пересчета индуктивных сопротивлений по осям d и q , после чего из полученных сопротивлений повторно инициализируется значение ЭДС для учета насыщения системы. Аналогичное использование ХХХ, как способа учета насыщенности системы используется и в расчетах по мгновенным значениям [2]. Но широкого применения использование ХХХ в задачах расчета синхронных машин в России на уровне требований и стандартов никогда не было, поэтому рекомендуется апробировать этот метод.

Для расчета токов короткого замыкания (КЗ) на Западе традиционно используют насыщенные параметры генератора [3]. Между тем в соответствии с российскими традициями ненасыщенные параметры до сих пор используются при построении модели схемы замещения генератора и расчете переходных процессов в электрических системах. На сегодняшний день вопросов по этому поводу не было.

Индуктивное сопротивление, используемое для расчетов синхронных машин, является величиной, представляющей величину магнитного потока на единицу намагничивающей силы, т. е. прямым образом зависит от того, по какому пути в данный момент замыкается магнитный поток, который динамически изменяется в процессе работы под воздействием внешних магнитных потоков и величины магнитной проводимости материала, которая также изменяется [4]. Влияние внешних магнитных потоков приводит к тому, что синхронное сопротивление переходит в сверхпереходное, которое затем становится переходным (рис. 1).

Несмотря на то, что предэксплуатационный запуск генератора проводится для выявления насыщенных параметров и что в программных комплексах есть ХХХ для пересчета параметров модели, по результатам валидации модели с ненасыщенными параметрами инженеры пришли к выводу, что этого достаточно.

Насыщенность системы определяется тем, какая в текущий момент магнитная проводимость контура магнитного поля. Синхронная машина может стать насыщенной в процессе, когда нарушен баланс между полем статора и ротора в ту или иную сторону. В первом случае это связано с режимами КЗ и асинхронного хода, а во втором – с режимами резкой значительной разгрузки.

На сегодняшний день в расчетах генератора недостаточно внимания уделяется учету насыщения генератора в процессе переходных процессов. Индуктивные сопротивления в насыщенном состоянии меньше, чем в ненасыщенном, на 10–20 %, в результате при использовании сопротивления, не соответствующего действительности, токи могут

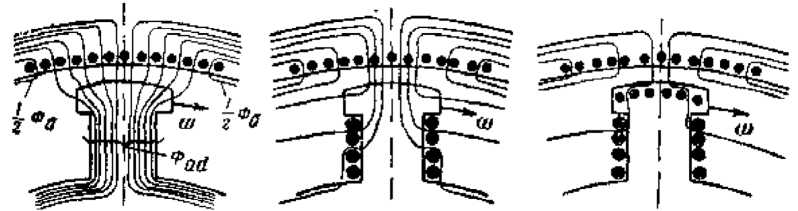
а)                                      b)                                      с)

Рис. 1. Магнитные потоки в продольной оси ротора, определяющие синхронную реактивность (а), переходную реактивность (b) и сверхпереходную реактивность (с)

Fig. 1. Magnetic fluxes in the longitudinal axis of the rotor, determining synchronous reactivity (a), transient reactivity (b) and super-transient reactivity (c)

отличаться также на 10–20 %. О необходимости учета насыщения в задаче расчета синхронных машин ранее упоминалось в [5, 6]. Однако в России традиционно используется расчет по ненасыщаемым параметрам. Данные расчеты выполняются без учета ХХХ, независимо от режима работы генератора.

Целью данного исследования является описание и изучение насыщения в синхронной машине. Это явление исследуется с помощью моделирования различных режимов с использованием метода конечных элементов и модели Парка – Горева. Кроме того, гипотезы подтверждаются практическими результатами сравнения разницы между измеренными и имитационными сигналами тока, полученными при воспроизведении по данным синхронных векторных измерений с различными индуктивными сопротивлениями.

Моделирование

• А.    Описание процессов насыщения

с использованием МКЭ

Для иллюстрации процесса насыщения стали статора использовалась модель генератора, описанная в [7]. Данная модель выполнена для генера- тора ТВВ-320 российского производства. Магнитное поле рассчитывалось методом МКЭ. Электротехническая сталь имеет нелинейную зависимость B(H) для статора и ротора. Кроме того, в реальном генераторе используется холоднокатаная сталь, которая является анизотропным материалом, ее магнитная проводимость вдоль одной оси больше, чем вдоль другой. Этот эффект необходимо учитывать, чтобы правильно выявить факт насыщения зубцовой зоны генератора. В модели анизотропность стали учитывается тем, что в зубце используется одна кривая намагничивания, описывающая магнитные свойства материала, а в остальной части статора – другая кривая намагничивания, соответствующая меньшей магнитной проводимости. Это допустимо в связи с тем, что магнитный поток в основном направлен вдоль зубца и поперек дна паза.

На рис. 2 показана кривая намагничивания стали статора по продольной оси, из которой состоит статор. По этой характеристике сталь считается насыщенной, когда магнитная индукция превышает 1,7 Тл.

На рис. 3 показано распределение магнитной индукции сначала в нормальном режиме, а затем в

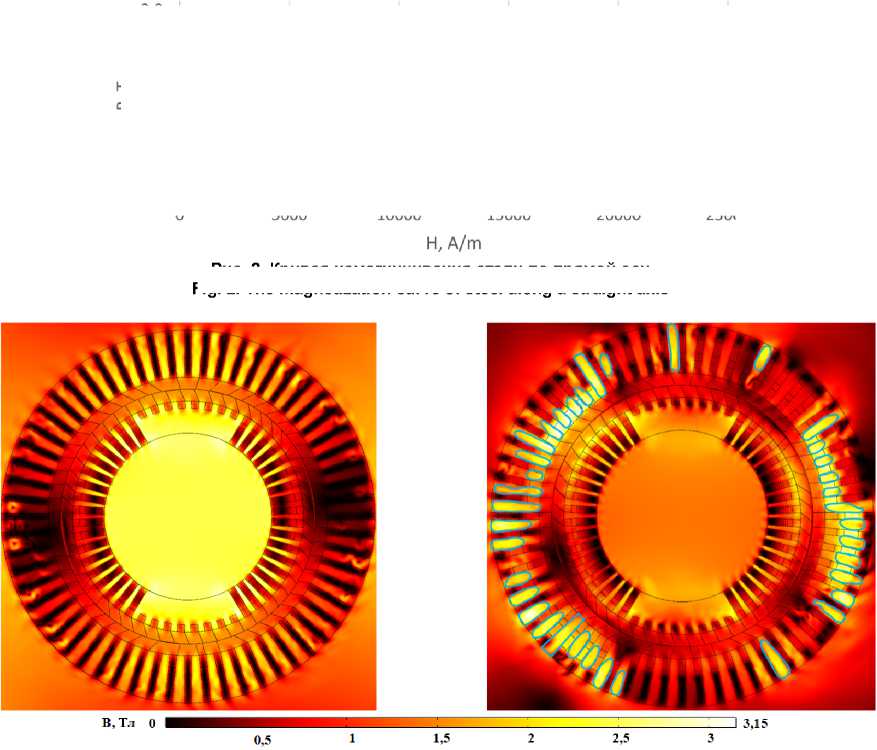
а)

b)

Рис. 3. Распределение магнитной индукции: нормальный режим (а), режим двухфазного КЗ (b)

Fig. 3. Magnetic induction distribution: normal mode (а), two-phase short circuit mode (b)

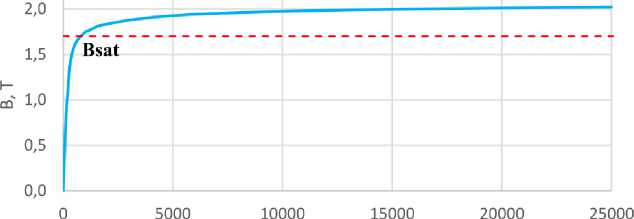
Рис. 2. Кривая намагничивания стали по прямой оси Fig. 2. The magnetization curve of steel along a straight axis

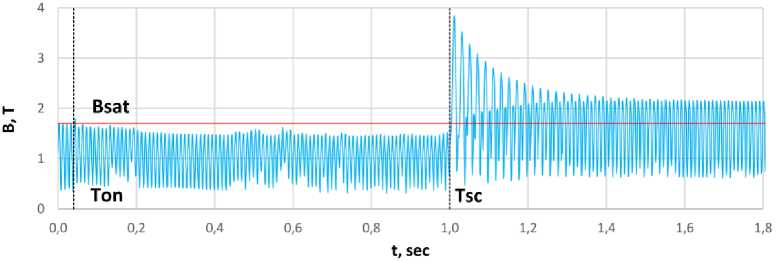
Рис. 4. График изменения магнитной индукции в зубце при КЗ

Fig. 4. Graph of changes in magnetic induction in the tooth at short circuit

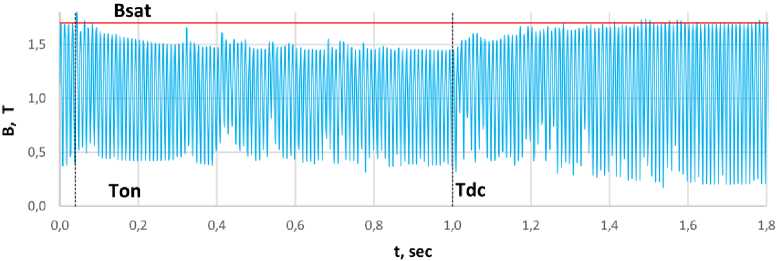
Рис. 5. График изменения магнитной индукции в зубце генератора при выделении энергорайона на изолированную работу

Fig. 5. Graph of changes in magnetic induction in the tooth of an electric generator when allocating an energy district for isolated operation

режиме двухфазного КЗ. Цветным градиентом отображается уровень магнитной индукции.

Видно, что насыщение стали имеет неравномерный характер при КЗ. Сталь насыщается вокруг пазов статора, в которых плотность магнитной индукции выше. В литературе это явление известно как размагничивающее действие реакции якоря [8]. Зоны зубцов статора, в которых магнитная индукция выше 1,7 Тл, выделены голубым цветом. В области вокруг пазов с высокой плотностью тока магнитное поле искажается и магнитная проводимость становится максимальной.

В результате неоднородность картины поля свидетельствует о неприемлемости использования параметров модели, полученных из экспериментов с нормальным режимом, описанных в [9].

На рис. 4 показано усредненное по площади зубца статора мгновенное значение магнитной индукции в режиме работы на холостом ходу до 0,04 с, затем генератор включается в сеть, а с 1 с обмотки статора фазы В и С замыкаются между собой. При этом ток статора резко возрастает, но ток возбуждения остается прежним, в результате чего увеличивается уровень магнитной индукции в зубцах и насыщает сталь. В этом случае большинство зубцов статора находится в состоянии насыщения, поэтому генератор будет характеризоваться насыщенными параметрами переходного и сверхпереходного сопротивления.

На рис. 5 показано усредненное по площади зубца статора мгновенное значение магнитной индукции в режиме работы на холостом ходу до 0,04 с, затем генератор включается в сеть и через 1 с отключается от системы. При этом ток статора резко уменьшается, а ток возбуждения остается прежним, в результате чего увеличивается уровень магнитной индукции в зубцах и сталь синхронной машины находится практически в насыщенном состоянии. Красным цветом на обоих графиках отмечен уровень 1,7 Тл, определяемый границей насыщения. В этом случае максимальные значения магнитной индукции незначительно превышают границу насыщения, поэтому генератор можно скорее считать ненасыщенным.

• B.    Сравнение моделей с учетом насыщения и без учета насыщения

Для сравнения качества моделей использовался аналогичный метод [10, 11]. Дело в том, что для воспроизведения событий в рамках исследуемой математической модели необходимо использовать данные СВИ, измеренные на реальном оборудовании (в нашем случае на генераторе). Парадигма воспроизведения представлена на рис. 6. Она предполагает воспроизведение амплитудных и частотных сигналов вектора напряжения с каждой фазы выводов статора, напряжения возбуждения и скорости вращения ротора.

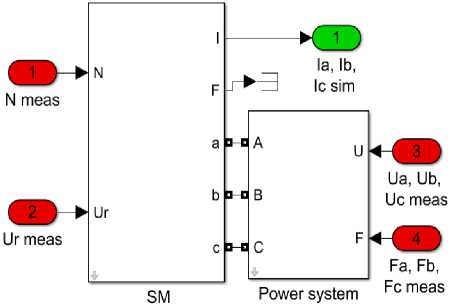
Рис. 6. UF(N,Ur) – воспроизведение Fig. 6. UF(N,Ur) – playback

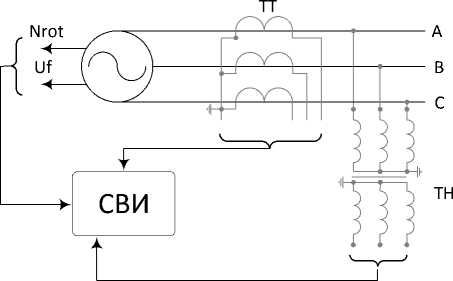
Рис. 7. Схема подключения измерительных приборов

Fig. 7. Measuring tools wiring diagram

Регистрировались сигналы текущих векторов, затем экспертно и численно оценивалось качество модели с помощью функции наименьших квадратов (SSE):

SSE = E C₌0 ( S m ^ ( t ) - S ts™ ( t ) ) 2 ,           (1)

где C – номер образца; S_i^meas , S_i^sim – измеренные и смоделированные сигналы модели в момент времени t .

Для использования этой функции важным примечанием является то, что измеренные и смоделированные сигналы должны иметь один и тот же шаг расчета данных. «Нагрузка» (ток) статора в этой парадигме определяется разницей между ЭДС ротора и вектором напряжения статора.

Объектом исследования был генератор производства BRUSH типа DG185ZL-04. В технической документации, предоставленной производителем, приведены ненасыщенные, насыщенные сопротивления генератора и ХХХ (раздел V). Программное обеспечение MATLAB Simulink использовалось в качестве основы для воспроизведения событий. Использовался стандартный блок Synchronous Machine PU, основанный на уравнениях Парка – Горева. В этом блоке учитываются:

• •    переходные процессы в цепях возбуждения и демпфирование;

• •    потери на трение;

• •    ХХХ.

Этого достаточно, чтобы оценить влияние насыщения на моделирование переходных процессов.

Для определения правильных параметров в условиях различных возмущений были проверены три набора параметров генератора:

• 1)    генератор с насыщенными параметрами (Sat);

• 2)    генератор с ненасыщенными параметрами (Uns);

• 3)    генератор с ненасыщенными параметрами и ХХХ (UnsNLC).

Для проверки параметров были выбраны два события: режим с выделением энергорайона, в котором функционирует исследуемый генератор, на изолированную работу и режимом КЗ. СВИ регистрировал данные этих событий с помощью ряда сигналов: напряжения возбуждения, частоты вращения ротора, частоты напряжения и тока каждой фазы, частоты напряжения каждой фазы. На рис. 7 представлена схема подключения измерительных приборов.

В работе использовались измерения с гарантированной, соответствующей предельной погрешности точностью УСВИ класса М [12]. События выбраны с учетом влияния погрешностей измерения трансформаторов тока (ТТ) и напряжения (ТН). Из условий применения на генераторе ТТ типа ТКБ-10-5 10 кВ 2500/1 и диапазона допустимых токов СВИ класса М в статических условиях 2 I nom один из основных критериев определяется максимальным значением тока статора, т. е. 5 кА. Номинальное напряжение ТН по номинальному напряжению генератора ограничено от 0,2 U nom до 1 , nom .

Было экспертно установлено, что в доаварий-ных режимах генератор не был в насыщении, а частота сети соответствовала номинальной, поэтому для всех наборов параметров синхронные сопротивления одинаковы и соответствуют ненасыщенным.

Результаты

В результате моделирования были получены графики I ( t ) и U ( t ) в о. е., определяющие поведение генератора при выделении энергорайона на изолированную работу, что показано на рис. 8, и КЗ, что показано на рис. 9. Стоит отметить, что в первом случае просадка напряжения и увеличение тока статора генератора определяется возникновением существенного дефицита мощности в изолированной энергосистеме, во втором – характерными для КЗ электромагнитным переходным процессом. В первом случае модель показала наилучшие результаты с ненасыщенными параметрами, во втором – с насыщенными. Заметим, что из-за значи-

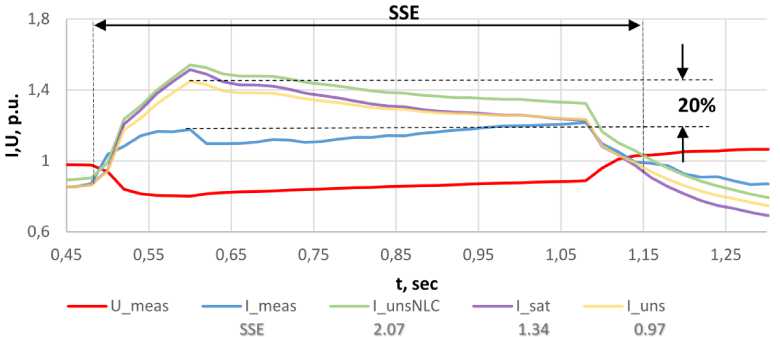
Рис. 8. График изменения тока и напряжения статора в результате выделения энергорайона на изолированную работу

Fig. 8. Graph of changes in the current and voltage of the stator as a result of the allocation of the energy district for isolated operation

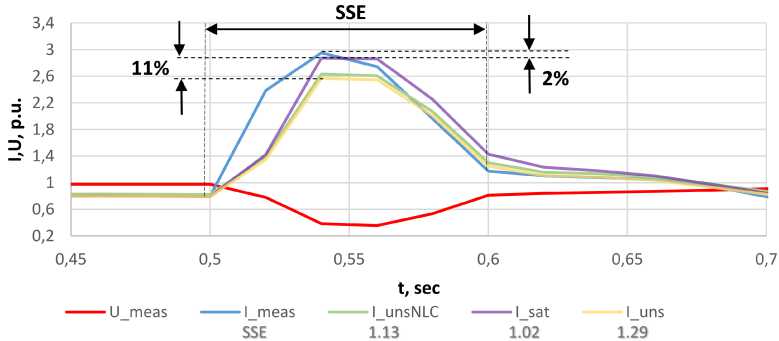
Рис. 9. График изменения тока и напряжения статора в результате удаленного КЗ Fig. 9. Graph of stator current and voltage changes as a result of remote short circuit

тельной погрешности «наилучшего» случая в 20 % для выделения энергорайона на изолированную работу необходимо идентифицировать параметры модели и сравнивать их с другими параметрами. Значения SSE, которые определяются как разница между смоделированным и измеренным сигналом, показаны на рис. 8 и 9.

На рис. 8 и 9 используются следующие обозначения: U_meas – измеренное напряжение статора; I_meas – измеренный ток статора; I_unsNLC – смоделированный с помощью ненасыщенных параметров и ХХХ ток статора; I_sat – смоделированный ток статора с использованием насыщенных параметров; I_uns – смоделированный ток статора с использованием ненасыщенных параметров.

Приемлемые результаты были получены во втором случае. Стоит обратить внимание на то, что минимальную SSE имела модель с насыщенными параметрами. Это означает, что генератор насыщается в режиме КЗ.

Важно отметить, что модель с ненасыщенными параметрами и ХХХ, к сожалению, не стала универсально точной как для событий, так и для всего уровня насыщения. Этот вопрос требует дополнительного изучения с помощью процедуры проверки ХХХ, а также алгоритма пересчета сопротивления.

Выводы

В работе было произведено исследование процессов насыщения в турбогенераторах, дано их численное и графическое описание. С помощью модели МКЭ показано, что в условиях переходных процессов вследствие КЗ или на холостом ходу сталь синхронной машины может уходить в насыщение.

Модель Парка – Горева имеет ограничения из-за принятых при ее разработке допущений и ее дискретности, т. е. при моделировании генератора можно использовать шесть вариантов схемы замещения: синхронные, переходные и сверхпереходные, которые могут быть насыщенными и ненасыщенными. Поэтому выбор между насыщенным и ненасыщенным параметрами для каждого генератора является индивидуальным. Чтобы сделать вывод о необходимости использования на- сыщенных параметров при удаленных КЗ, необходимы дальнейшие исследования с помощью анализа больших данных СВИ.

По результатам сравнения моделей с насыщенным и ненасыщенным параметрами при коротком замыкании (см. рис. 9) видно, что разница между сигналами модели с использованием насыщенных параметров по сравнению с ненасыщенными параметрами определяется уменьшением максимума тока на 11 % в первый момент КЗ, т. е. является значительным.

Судя по экспериментальным данным и замерам, полученным с СВИ, можно утверждать, что при близких КЗ стоит использовать насыщенные параметры генератора для получения более точных результатов по сравнению с моделью с ненасыщенными параметрами и моделью с ненасыщенными параметрами с использованием ХХХ, независимо от страны и производителя генератора.

Использование же насыщенных параметров при ХХ, форсировке возбуждения или изменении нагрузки (выделении на изолированную работу) не рекомендуется, но при расчетах и сопоставлении результатов с замерами параметров генератора стоит учитывать, что насыщение могло произойти в зависимости от величины остаточной намагниченности из предыдущего режима и соотношения поля ротора и статора.

Модель Парка – Горева для моделирования генератора в масштабах энергосистемы на сегодняшний день – самый оптимальный вариант. Модель генератора с использованием МКЭ трудозатратна и требует больших вычислительных мощностей.

В дальнейшем планируется разработать модель генератора с использованием метода конечных разностей FDTD на принципе Yee-алгоритма. Такой способ расчета позволит моделировать генератор аналогично МКЭ, но при этом расчет можно сделать с использованием параллельных вычислений.

Проведенные эксперименты с помощью модели МКЭ показали, что резкое увеличение тока статора приводит к насыщению стали синхронной машины. Несимметричные режимы приводят к неравномерному распределению магнитной индукции. Это говорит о том, что из-за использования симметричных режимов при испытаниях КЗ и ХХ для определения параметров схемы замещения имеет значительную погрешность при расчете несимметричных режимов. Для получения более точных параметров схемы замещения предлагается использовать метод частотного анализа для идентификации индуктивностей генератора.

Приложение: Параметры синхронной машины

Общие параметры:

S = 27,7 МВА U = 10,5 кВ нн	f н = 50 Гц
Tq ′ = 1,15 с         Td ′′ = 0,04 с Xl = 0,33          Rs = 0,01 Ненасыщенные параметры:	Tq ′′ = 0,04 с
X di = 2,47          X d ′′ i = 0,33 Х qi = 1,26          X q ′′ i = 0,5 Насыщенные параметры:	X d ′′ i = 0,21
X di = 2,13          X d ′ i = 0,27 Х qi = 1,09          X q ′′ i = 0,33	X d ′′ i = 0,19