Исследование неоднородного уширения линии ЯМР в дисперсии парамагнитных наночастиц

Считается, что неоднородное уширение линии ЯМР жидкости в однородном внешнем магнитном поле наблюдается, если в ней присутствуют парамагнитные или диамагнитные частицы размером больше микрона [1]. Однако в работах [2, 3] методом спин-эха наблюдалось проявление неоднородного уширения в жидкости, содержащей парамагнитные частицы размером 10 нм. Парамагнитные наночастицы на основе магнетита применяются в наномедицине [4]. Естественные парамагнитные наночастицы (гемы) содержатся во многих живых тканях [5]. Создаваемое этими наночастицами неоднородное уширение линии ЯМР вносит искажения в ЯМР-томограммы и спектры высокого разрешения биологических объектов. Поэтому изучение неоднородного уширения линии ЯМР в присутствии магнитных наночастиц является актуальным. В настоящей работе получена зависимость неоднородного уширения от концентрации парамагнитных наночастиц, которая ранее не исследовалась.

ИЗМЕРЕНИЯ И РАСЧЕТЫ

Исследуемая магнитная дисперсия — стабилизированный олеатом натрия коллоидный раствор в воде однодоменных частиц магнетита размером около 10 нм. Сигнал ЯМР протонов растворителя регистрировался импульсным спектрометром С-200 фирмы Bruker с рабочей частотой f 0 = = 200 МГц, источником магнитного поля в виде сверхпроводящего соленоида и цилиндрическим датчиком диаметром 5 мм с осью, параллельной напряженности поля.

На рис. 1 приведены записи линий ЯМР протонов двух образцов магнитной дисперсии с разными концентрациями магнетита С, полученными путем разбавления водой исходной дисперсии с объемной концентрацией магнетита С0 = 2.7 %. По оси абсцисс отложена разница установленной напряженности магнитного поля Н спектрометра ЯМР и напряженности этого поля H0 , при которой наблюдается максимум сигнала ЯМР от протонов эталонного вещества, в качестве которого

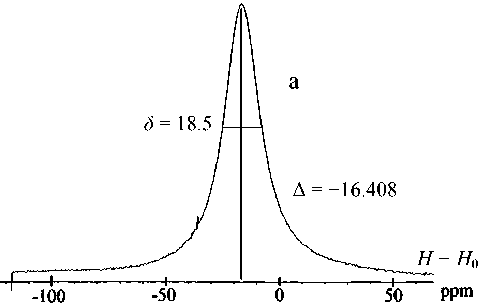
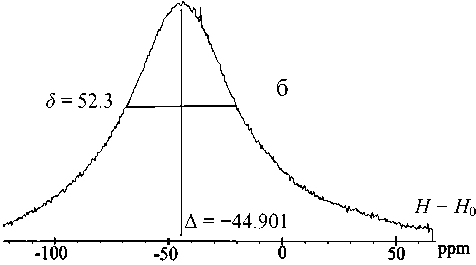
Рис. 1. Записи сигналов ЯМР протонов магнитной дисперсии при объемных концентрациях магнетита С = 0.1 С0 (а) и С = 0.2 С0 (б). Химический сдвиг А относительно сигнала воды и ширина 3 указаны в миллионных долях (ppm), 1 ppm = 3.74 Ам взят чистый растворитель (вода). Из рис. 1 можно определить химический сдвиг А (величину H - H0, при которой сигнал 1H ЯМР от магнитной дисперсии максимален) и ширину линии на полувысоте 5. На рис. 2 приведены зависимости А и 5 от объемной концентрации С магнетита. Из рисунка видно, что химический сдвиг А пропорционален С, а 5 с ростом C увеличивается нелинейно.

Приведенную на рис. 2 зависимость А от С можно представить в виде

А = - K а - C ,                   (1)

где K _А = 6.9 - 10 4 А/м. Подробно зависимость А от С исследована в [6].

Ширина линии 5 складывается из однородного

5 ₀ и неоднородного 5 H уширений [7]:

5 = V 5 2 + 5 Н .

Однородное уширение в коллоидных растворах обычно пропорционально концентрации [8]

5 о = K 0 С ,                   (3)

где коэффициент K ₀ от С не зависит. Неоднородное уширение также представим пропорциональной зависимостью

Из (2–4):

5 = 7 K О + KH - C             (5)

и модуль отношения равен

5 _ У ^K о ² + K H

А "    K а

На рис. 3 приведена экспериментальная зависимость 5 /А| от С , из которой видно, что с ростом С отношение 5 /А| уменьшается, что, согласно (6), говорит об уменьшении K_H с ростом С . Из рис. 3 также видно, что при ( C/C 0 ) > 0.8 отношение | 5 А| от С практически не зависит. Это означает, что при C/C 0 ® 1 K H <<  K 0 и, из (6):

5 = K

А    K а .

Из рис. 3 также следует, что при CC ₀ ~1 отношение | 5 /А| = 0.5, откуда с учетом (7) получается значение K ₀ = ^2-, подставив которое в (3) и

KC А _ /А² , ~ (5), получаем о ₀ = 2 = у и 5 = J — + о_н , от-

5 н = К_н - С .                    (4)

куда находим связь неоднородного уширения

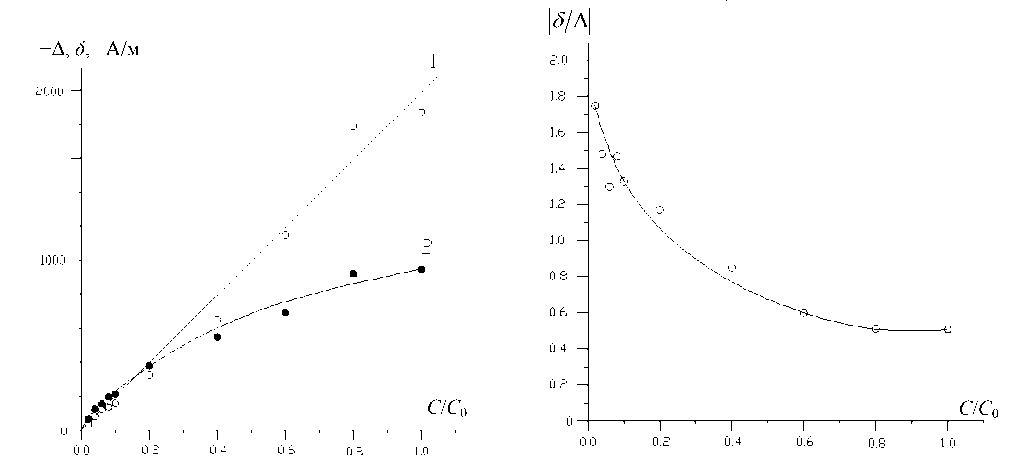
Рис. 3. Экспериментальная зависимость модуля отношения 5 /А| от объемной концентрации С магнетита

Рис. 2. Экспериментальные зависимости химического сдвига А (1) и ширины сигнала на полувысоте 5 (2) от объемной концентрации С магнетита

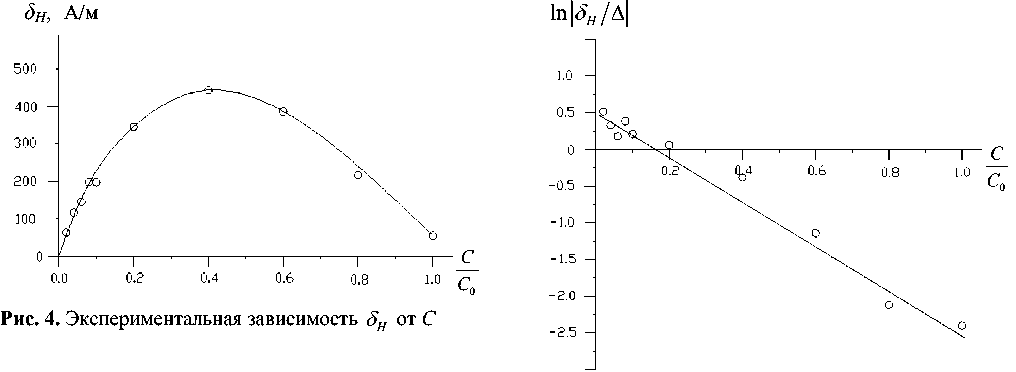
с экспериментальными величинами ∆ и δ :

Рис. 5. Экспериментальная зависимость ln от С

^δ H ⁼

.

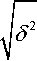
∆ ²

δ _H ∆

Подставив в (8) экспериментальные значения δ и ∆ , приведенные на рис. 3, получили зависимость δ _H от С, отраженную на рис. 4. Она может быть представлена эмпирической формулой

δ H = aK ∆ Ce ^{- bC} , (9)

где а и b — коэффициенты, не зависящие от С .

Для проверки адекватности формулы (9) эксперименту ее удобно разделить на ∆ и представить в виде

^{δ H} = ae ^{- bC} ∆

.

Прологарифмировав (10), получаем ln δ _H /∆ = = ln a - bC .

На рис. 5 построена зависимость ln δ _H /∆ от С/C ₀ , полученная из экспериментальных результатов, приведенных на рис. 4. Она близка к линейной, что говорит в пользу адекватности выражения (10). Из нее — значения коэффициентов a = 1.8, b = 113.

ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Теоретический расчет сдвига и неоднородной ширины линии ЯМР в дисперсии сферических частиц в цилиндрическом датчике с осью, ориентированный нормально напряженности магнитного поля, приведен в [9]. Из него следует, что теоретические величины сдвига и ширины определяются формулами (1), (4) с коэффициентами

K _∆ = 10⁵ А/м , K_H = 4.2 ⋅ 10⁵А/м . При этом коэффициент K_Н и отношение δ _Н /∆= 8.4 не зависят от С .

Отличие в два раза полученного в настоящей работе экспериментального значения K _∆ от теоретического можно объяснить тем, что в работе [4] не учитывалась агрегация частиц, которая в результате замыкания части создаваемого частицами магнитного потока внутри агрегатов должна приводить к уменьшению ∆ .

Меньшие теоретических экспериментальные значения K_Н и δ _Н I ∆ , а также их зависимость от С можно объяснить влиянием статистических процессов усреднения локальных полей частиц и образованием конгломератов. В частности, уменьшение δ _Н /∆ с ростом С на рис. 3 можно объяснить, исходя из того, что сдвиг ∆ пропорционален средней намагниченности J_ср , создаваемой наночастицами в объеме образца, а ширина линии δ _H пропорциональна среднему квадратичному локальных отклонений намагниченности ∆ J в разных точках образца. Напряженность магнитного поля спектрометра С-200 обеспечивает намагничивание дисперсии до насыщения. При этом J_ср = µ n_ср , ∆ J = µ ⋅∆ n , где µ — магнитный момент частицы, n ср — средняя концентрация частиц, ∆ n — средняя квадратичная флуктуация локальной концентрации частиц. В результате δ ∆ n

H = . Как известно, величина относительной ∆ nср флуктуации концентрации частиц ∆n nср с ростом nср уменьшается пропорционально 1 nср . Следовательно, по этой причине с увеличением С отношение δН ∆ должно уменьшаться пропорционально 1 C . Появление конгломератов уменьшает nср , приводя к росту δН ∆ .

Уменьшение δ _H с ростом С на рис. 4 можно объяснить тепловым движением молекул. Известно, что если действующие на движущуюся молекулу локальные поля частиц меняются со временем корреляции τ , то неоднородная ширина линии ЯМР δ _H пропорциональна τ [1]. Время τ связано с масштабом неоднородности l и коэффициентами самодиффузии D формулой Эйнштейна τ = l ² (2 D ) . За масштаб неоднородности можно принять длину свободного пробега молекулы между столкновениями с частицами λ = 1 ( σ n ) ( σ — сечение столкновения, n — концентрация частиц). Подставив n = CV ( V — объем частицы), получаем τ = V ² ( 2 DC ² σ ² ) . В результате ширина δ _H пропорциональна 1 C ² . Появление конгломератов вследствие уменьшения n должно увеличивать λ , приводя к росту δ _H .

пользовать для изучения структуры магнитных дисперсий, играющей большую роль при их практическом применении.