Исследование нестационарных движений физических систем

Рассмотрим нестационарную голономную систему с идеальными связями, положение которой определяется n обобщенными координатами Q . Математическую модель такой системы можно представить уравнениями Лагранжа d ЭТ дТ _ dt 9 q dq '             (1)

где кинетическая энергия

7 = Г₂ + 7\ + T_o , T₂(t,q, q) =^q^T(t,q)q

Tjfcg, q)= B^T(t, q)q, ^(t, V) =     ), (3)

где A(t, q) – матрица размерности n H n, B(t,q) – матрица-столбец размерности n H 1, C(t, q) – скалярная функция, Q = Q(t,q,q) – матрица-столбец размерности nЧ1 обобщенных сил, действующих на систему.

При этом предполагаем, что функции переменных C^ Q ) являются дважды непрерывнодифференцируемы и ограничены вместе со своими производными физическими свойствами исследуемого объекта.

Вектор обобщенных сил Q можно представить в виде суммы

Q^,q>4)=Qy(t,q,q) + Qb(t,q), (4) где Qy =          – n-вектор управляющих сил, который необходимо определить, а Qb= (^.» Q) – n-вектор внешних сил.

Учитывая выражение кинетической энергии (2), уравнения (1) можно привести к виду

d dT₂ dT₂ dt dq dq

dt dq ^ Q)   Qb , (5)

Если ввести новые обобщенные координаты x = q- q(t), то структура уравнений (3) в силу линейности оператора предложенной замены не изменится. При этом в новых переменных кине- тическая энергия системы имеет вид

T=                              =

=

+ B^T(t,x + q(t))(x + q(t)) +

+C(t,xr + q(t)) =

, где

A(t,x) = A(t,x + q(t)) ,

B(t,x) = B(t,x + q(t)) + A(t,x + q(ty)q(t),

C(t,x) =^q^T(t)A(t,x + q(t))Q(C +

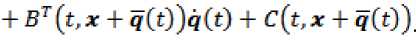
В результате указанной замены изучение поведения решений системы (1) в окрестности программного движения ( q.q) сводится к изучению поведения решений преобразованной системы в окрестности x = x = 0 . Поэтому, без ограничения общности, можно считать, что обобщенные координаты Q выбраны таким образом, что программное движение системы определяется тождеством q — 0, q =0.

Будем искать вектор управляющих сил Q_y(t, q. q) в виде

=

=                                              . (6)

Для существования программного движения вектор сил Qy(t,q) должен удовлетворять соотношению

Q^t, o) = -Q_b (t, o) - ^ (t, o) + ^(t, o) . (7)

Если при этом

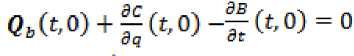
, при всехtER , тогда следует, что

<^М = 0 .

Допустим, что действие управляющих и внешних сил представимо в виде

Qy(t,q) + Qb^q^-^^t-q) +

Эс ^ л _    ^ ^ 9S(t,q}

⁺ -(t,q) = -p(t,q) — ^,

где функции p(t,q"),dS(t,q) удовлетворяют условиям

0 < p₀< p(t, q) < p_t , где Po , Pi – постоянные,

S(t,q_Q) = 0,^| (t,q₀) = 0

Тогда уравнение движения (5) принимает вид d ^ат„\ ат, as , =-P^+G 4 + Qy. (9) at \ cq J dq         dq                   v 7

Решение уравнения (9) позволяет получить зависимость оптимальных входных сигналов от параметров системы с целью получения необходимого сигнала на выходе.

Рассмотрим задачу о стабилизации некоторого нестационарного движения физического маятника fl = y₀(t) , которое создается регулируемой скоростью вращения вокруг вертикальной оси. Уравнение движения маятника имеет вид

АУ = — (mgz₀ + (C — S)2(t) cost?) sin У. (10)

Пусть закон вращения щ = щ(t) вокруг вертикальной оси таков, что осуществляется нестационарное движение маятникаУ = y0(t), то есть w2(t)(C — 5) cosi90(t) sini90(t) =

= ЛУ₀(1) + mgz₀ sin У_о (t) , при этом будем предполагать, что ω (t) представляет собой ограниченную функцию.

Введем x = У — У_о (t) – отклонение истинного движения от программного. Допустим, что в оси качания действует стабилизирующий момент, типа момента вязкого трения, M_y = —kx , где к = const >  0 .

Из (10) находим, что уравнения возмущенного движения будут иметь вид

,

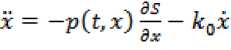
где где ,

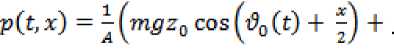
+ (C — S)to2(t) cos2^i90(t) +j) cos^

При выполнении условий

p(t, 0) >  Pq = const > 0 ,

— (Znp(t,0)) > — 2k0 + a0

(a0 = const > 0) , или p(t, 0) = mgzQ cos Уо (t) +

+ (C — 5) p0 > 0, it _ 2£>5^£2iLEi£i£**LL£lI^£°£52^Lli^£z^wV^i!*iifLi£l^Ll£^ Д 1                   ffl#^vcu»#4(i)f(C"^)e#x(iJre*M^(i)                , где aT = const > 0 (12)

То есть при выполнении условий (12) имеем равномерную асимптотическую устойчивость положения x = 0 системы (11) или равномерную асимптотическую устойчивость заданного нестационарного движенияУ = ^(t) системы (10). Из этой равномерно асимптотической устойчивости следует также равномерная устойчивость при любых постоянно действующих возмущениях.

В общем случае, условия (12) можно представить как условие определенно-положи-тельности второй вариации 5 на движении » = ^(t) и условие ограниченности логарифмического изменения этой вариации во времени снизу значением 2к0.

Исследуем устойчивость нестационарных движений центрифуги, изображенной на чертеже (рис. 1). Кабина M центрифуги представляет собой твердое тело, которое может свободно поворачиваться вокруг оси OO' относительно державки AOO'. Ось OO' ортогональна плоскости L, проходящей через ось AD центрифуги и центр масс S кабины. Державка AOO' приводится во вращение вокруг неподвижной оси AD, при этом скорость вращения изменяется согласно заданному закону ω = ω (t) . За обобщенную координату примем угол α – угол поворота кабины вокруг оси OO'.

Пусть L – плоскость симметрии кабины, а ось Ox , проходящая в этой плоскости через точку S и пересекающаяся с осью OO' в точке O, является главной осью центрального эллипсоида инерции. Обозначим через A, B, C моменты инерции кабины M относительно осей Ox, Oy, Oz , рассто-

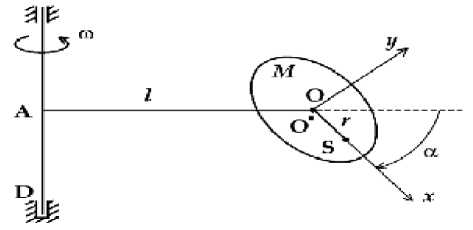
Рис. 1. Устойчивость нестационарных движений центрифуги

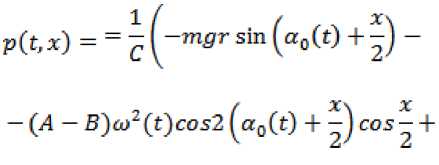
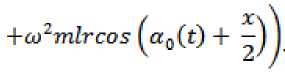
При выполнении условий

p(t, 0) > p₀ = const > 0,

яние OA через l , расстояние OS через r . Кинетическая энергия кабины имеет вид

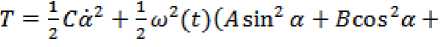
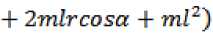
или

Т = Т Т Т 1                 1            ,

Т₂ = ^Са² К = О

'      2         ^, 1        ^,

Tq = -о>²(£)(Л sin² а + Bcos²a +

+ "Zmlrcosa + ml²) .

Потенциальная энергия кабины в поле тяжести имеет вид силы

П = mgr sin a.

Предположим также, что в шарнирных опорах OOґ действуют силы вязкого трения, образующие момент M = — к a , где к = const > О . Запишем уравнения движения

Ca = —mgr cos a + 2(t) H

H((Л — B) cos a — mlr^ sin a — ka . (13)

Пусть регулируемое вращение державки AOOґ вокруг оси AD по закону щ = щ(t) таково, что осуществляется нестационарное движение кабины a = a0(t), то есть имеет место соотношение co2 (t)((Л — B) cos cr0 — mlrj sin a0(t) =

.

При этом будем предполагать, что ω (t) представляет собой ограниченную функцию.

Рассмотрим задачу об условиях устойчивос- ти указанного нестационарного движения a = a0(t) . Уравнение возмущенного движения можно привести к виду x = — pvt.x) - k^,      (14)

гдеx = a — a0(t) – отклонение истинного движения от программного, ки = - 5(л) = 4(1 — cos-)

¹     c^,               X            2 ^,

— (lnp(t, 0)) > —2кг + a2, где a2 = const > 0

или

—mgr sin a₀(t) + co²(t)(?nZr cos a₀ (t) —

— (Л — B)cos2a₀(t)) >  p_Q > 0

2k 2cu(t)w(t)((4 - 8)cos2a0(t) - mZrcosa0(t)) +

C ¹                    TngrsiTUZQ^t) 4                  ^,

+fmyrcosa:_D (t)+a)²(t)(mirsina:₀ (t)-2(A-B) sin2a₀ (t))Ja₀(t) +ш²(0((Д-В) cos2a_B (,t)—mlrcosa_B(.i))

где a_± = const > 0 .

То есть имеем равномерную асимптотическую устойчивость положения x = 0 системы (14) или равномерную асимптотическую устой- чивость заданного нестационарного движения a = a0(t) системы (13). Из этой равномерной асимптотической устойчивости следует также равномерная устойчивость при любых постоянно действующих возмущениях.

При отсутствии сил вязкого трения в опорах OO', т.е. когда M=0 , и при противоположном условии p(t, 0) < -p₀< 0, движение a = a₀(t) будет неустойчивым.

Рассмотрим задачу в предположении, что ось OO' параллельна оси AD центрифуги (рис. 2).

За обобщенную координату примем угол Я – угол поворота кабины вокруг оси OO'. Обозначим момент инерции кабины относительно оси OO' через I, расстояние OA через l, расстояние OS через r.

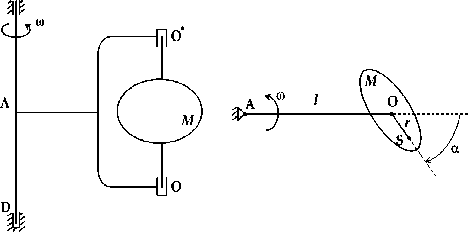
Рис. 2. К решению задачи в предположении, что ось OOґ параллельна оси AD центрифуги

Потенциальная энергия в рассматриваемом случае равна нулю. Кинетическая энергия имеет вид

Т = |z«² ~ a>(t)(mZrto(t) cos а + /)а +

+ -co²(t)(Z + mZ² + 2mZr cos a )

2                                                     , или

Г = T₂ + T_t + T_o , ,r₂ = |/<^ Т_г = —

Предположим также, что в шарнирных опо-

рах OO' действуют силы вязкого трения, образующие момент M = —Zea, где к = const > 0 . Запишем уравнения движения la = —to² (t)mZr sin a +

+ to(t)(2mZrco(t) cos a + 7) — ka . (15)

Пусть регулируемое вращение державки AOO' вокруг оси AD по закону co = 0(t). При этом будем предполагать, что "(t) представляет собой ограниченную функцию.

Рассмотрим задачу об условиях устойчивости указанного нестационарного движения a = a0(t) .

Уравнение возмущенного движения можно привести к виду x = —pvt.x) — — ktx ,      (16)

гдеx = a — a0(t) – отклонение истинного движения от программного, k. = - S(x) = 4(1 — cos-)

¹ i^{, v}           \             2 ^,

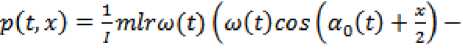
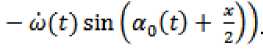
При выполнении условий

, p(t, 0) = 0(t) —

— 0(t)) > p₀ = const > 0 ,

^(lnp(t, 0)) > -2^! + a₂, где a₂ = const > 0, имеем равномерную асимптотическую устойчивость положения x = 0 системы (16) или равномерную асимптотическую устойчивость заданного нестационарного движения a = a₀(t). системы (15). Из этой равномерной асимптотической устойчивости следует также равномерная устойчивость при любых постоянно действующих возмущениях.

При отсутствии сил вязкого трения в опорах OO', т.е. когда M=0 , и при противоположном ус-ловииp(t, 0) < -p₀< 0, движение a = a₀(t) . будет неустойчивым.

Можно отметить, что условия равномерной асимптотической устойчивости программного движения в исследованных задачах можно представить как условие определенной положительности второй вариации приведенной потенциальной энергии или функции 5 на программном движении и условие ограниченности логарифмического изменения этой вариации снизу.

Таким образом, получена зависимость, которая позволяет указать оптимальные выходные сигналы функции параметров исследуемой системы с целью получения требуемого сигнала на выходе.