Исследование общего количества надземной биомассы в лесах в зависимости от взаимосвязи высоты и диаметра ствола деревьев

DOI:

Цитирование. Тахмазов Т. М. Исследование общего количества надземной биомассы в лесах в зависимости от взаимосвязи высоты и диаметра ствола деревьев // Природные системы и ресурсы. – 2023. – Т. 13, № 1. – С. 17–23. – DOI:

Введение. Показатель количества биомассы в деревьях является важным параметром для осуществления мониторинга состояния лесов [5]. Биомасса, содержащаяся в лесах, составляет основную часть всей биомассы, имеющейся в экосистеме, и позволяет определить скорость изменения состояния лесов [7; 8; 10]. Этот показатель также играет важную роль при планировании работ по лесоводству [4]. Количество биомассы в лесах имеет первостепенное значение при вычислении того убытка экосистеме, которое образуется из-за деградации и вырубки лесов, приводящих в конечном счете к генерации дополнительного количества СО₂, являющегося основным парниковым газом. Согласно [10], основными причинами деградации лесов и обезлесения являются:

• –    лесные пожары;

  – использование лесов в качестве пастбищ;

• –    болезни деревьев из-за различных вредителей;

• –    рубка деревьев;

• –    развитие населенных пунктов вблизи лесов.

Что касается абсолютного количества показателя биомассы в лесах, то этот пока- затель может быть измерен различными техническими средствами, используя как наземные, так и бортовые методы измерений. Некоторые значения этого показателя, приведенные в различных источниках приведены в таблице. Как видно из данных, для этой цели широко используются средства дистанционного зондирования, установленные в различных спутниках (Sentinel-2, Geo Eye-1, QuickBird и др).

В целом существуют схожие эмпирические формулы расчета показателя ABG (Aboveground Biomass) в зависимости от диаметра стебля и высоты деревьев [6; 10; 11; 13].

Целью настоящего исследования является выяснение условий достижения минимального значения показателя AGB в лесах в смысле выбора наилучшей функциональной зависимости между такими показателями как диаметр стебля и высота деревьев. Цель исследования, заключающаяся в достижении минимума показателя AGB, заключается в гарантированном обеспечении минимума биомассы в лесах, что в перспективе привело бы к усилению лесоохранных мер, к более точной оценке потенциала лесов аккумулировать карбон.

Способы оценки количества биомассы в различных типах лесов с использованием средств дистанционного зондирования

№	Тип лесов	Количества биомассы (AGB)	Сенсор	Литература
1	Леса частного сектора	72,54 мг/га	Sentinel-2	[2]
2	Мангровиальные леса	250,53 мг/га	GeoEye-1	[6]
3	Средиземноморской тип	38 тон/га	QuickBird	[10]
4	Лиственный	58 тон/га	ALOS PALSAR	[3]
5	Бореальный	39,5 мг/га	Landsat ETM+	[14]

Материалы и методы. Исходным предположением для построения предлагаемой зонной модели лесов является равномерный закон распределения деревьев в пределах некоторого типа леса в пределах фиксированной высоты деревьев (h₁ ÷ h₂), то есть:

где ρ – плотность вероятности распределения высоты деревьев.

При допущении (1) возможно построение зонной модели лесов, в которой лес состоит из некоторого количества воображаемых лесных зон, обладающих следующей особенностью упорядоченности высот деревьев в зоне. Требуемая упорядоченность деревьев в каждой из зон заключается в выполнении следующего условия налагаемой на показатели высот деревьев ( h ) в зоне:

h_t = h_i_₁ + Д/i;

Д/г = const i = l,n h_mtn< h_t< h_max

Таким образом, условия (1) и (2) позволяют нам в дальнейшем при проведении модельных исследований оперировать не всей территорией леса, а только одной воображаемой зоной, где условия (1) и (2) выполняются.

С учетом вышеизложенных исходных предположений проведем модельное исследование условий достижения минимальной величины показателя AGB в одной зоне, а следовательно, во всей территории исходного леса. Отметим, что существуют несколько различные эмпирические формулы для вычисления показателя AGB. Так, например, соглас- но [1], для вычисления AGB пригодна следующая формула:

AGB = 0,0509 ■ pD²h ,         (3)

где ρ – плотность; D – диаметр стебля на некотором фиксированном уровне; h – высота дерева.

В работе [2] приведены более уточненные формулы, раздельно для отдельных типов деревьев.

Так, например для акации:

AGB = 0,0775(D2/i)°-9018.(4)

Для тектоны (Teak):

AGB = O^UgCD2^)1’0835.(5)

Для остальных типов деревьев:

AGB = 0,0240(D2/i)°'7817.(6)

Для осуществления интегральной модельной оценки AGB также воспользуемся известными результатами по исследованию взаимосвязи показателей D и h .

Как отмечается в [12], традиционно, указанная взаимосвязь моделируется линейными уравнениями. В качестве примера на рисунке 1 приведены скаттерограммы, которые могут быть аппроксимированы линейными и нелинейными регрессионными уравнениями.

Отметим во многих работах (см. например: [9; 13]) приводятся сложные экспоненциальные регрессионные уравнения зависимости h = f ( D ). Вместе с тем существуют работы, в которых исследована обратная зависимость, то есть регрессионная связь:

D = φ ( h ).                    (7)

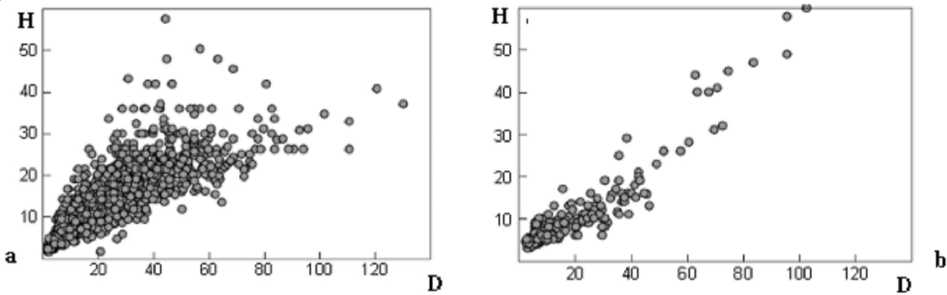
Рис. 1. Скатерограммы статической зависимости h от D , которые могут быть аппроксимированы нелинейными ( а ) и линейными регрессионными уравнениями ( b )

Например, согласно работе [14], такая статистическая связь может быть охарактеризована квазилинейным регрессионным уравнением (рис. 2).

С учетом вышеизложенного сформулируем задачу вычисления минимально гарантированного количества биомассы в одной зоне вышепредложенной зонной модели леса. В качестве функционала цели сформируем следующее выражение, используя базовую формулу (3):

, (8)

Решение оптимизационной задачи (20) согласно методу Эйлера должно удовлетворить условию

d^a.1D(h.")2h.+A.D(h.'y\ __

.

Из (12) получим:

Из (13) находим:

.                (13)

где a ₁ = 0,05099; D ( h ) – искомая оптимальная зависимость D от h при которой F достиг бы минимума. Для решения задачи (8) введем на рассмотрение следующее ограничительное условие:

.        (9)

Смысл условия (9) заключается в некотором ограничении пространства непрерывных и дважды дифференцируемых функций, в котором возможен подбор решения следующей безусловной вариационной задачи оптимизации:

.               (10)

С учетом (8) ^ (10) имеем:

,(11)

где X - множитель Лагранжа.

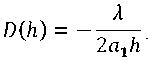
С учетом (9) и (14) вычислим λ. Имеем

.

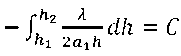
Из (15) находим:

2 а^ с

.                     (16)

hi

С учетом (14) и (16) получим

DW =

С

.

Мл

Покажем, что при решении (17) целевой функционал (20) достигает минимум. Для этого достаточно вычислить производную (13) по и убедиться, что полученный результат всегда

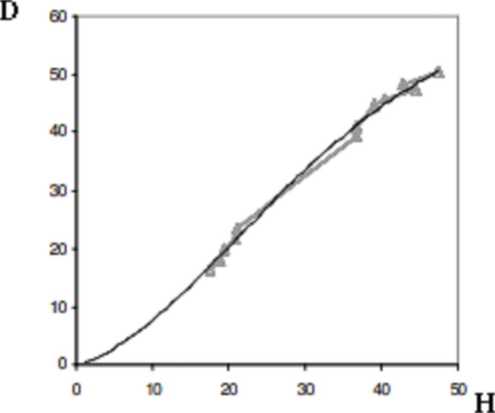
Рис. 2. Квазилинейная регрессионная линия взаимосвязи

является положительной величиной. Этот признак позволяет судить о том, что при решении (17) целевой функционал (11) достигает минимума.

Режим аналогичную оптимизационную задачу с применением выражения (6). На базе этого выражения составим следующий целевой функционал:

F₃ = ^a₂.(D(h.Wdh , (18)

Из (25) и (26) получим:

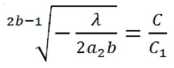
или

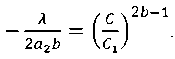
Из (28) получим:

где a ₂= 0,024; b = 0,7817.

.

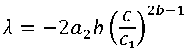
С учетом (7), (9) и (18) составим следующий целевой функционал безусловной вариационной оптимизации:

F01 = £a2-(D(hyhydh +

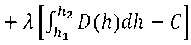
С учетом (23) и (28) получим:

Результаты и обсуждение. Анализ показывает, что решения сформулированных

Согласно методу Эйлера решение оптимизационной задачи должно удовлетворить условию:

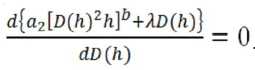
Из выражения (20) находим:

a₂b[D(h)²h]^{b 1}2D(h)dh + Л = 0.    (21)

Из (21) получим:

2a₂bh^bD(hy^b"¹ + Л = 0.       (22)

Из (22) имеем:

D(h) =

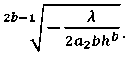
С учетом (9) и (23) получим:

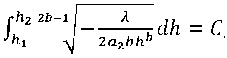
Выражение (24) запишем как:

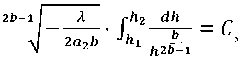
обозначив:

рЯ₂ dh _ _r h_t T ^L1 ^.

№-i

оптимизационных задач с использованием известных моделей для вычисления общего количества надземной биомассы деревьев дают схожие результаты. Как видно из (30) при b = 1 выражение (30) превращается в ранее полученное решение (17). При решении (30) целевой функционал (19) также достигает минимума, что может быть проверено проверкой знака производной выражения (21), который оказывается плюсовым, что подтверждает минимум функционала (19) при решении (30).

Таким образом, показано, что с учетом предложенной зональной модели леса, известной зависимости показателя AGB от диаметра стебля и высоты дерева, а также с принятым дополнительным условием налагаемым на функциональную зависимость D = D ( h ) суммарная биомасса лесов может достичь минимума при обратной зависимости D от h в виде функций (17) и (30), соответственно при рассмотрении моделей (3) и (6).

Заключение. Сформулирована и решена задача исследования зависимости суммарного количества биомассы в лесах, в частности показателей AGB, от взаимосвязи таких показателей деревьев как высота дерева и диаметр стебля деревьев. На основе предложенной зонной модели лесов, сформирован целевой функционал в двух вариантах, соответствующих известным выражениям зависи-

мости AGB от вышеуказанных показателей деревьев. Сформированы оптимизационные задачи с учетом налагаемого дополнительного ограничительного условия на функциональную зависимость диаметра стебля от высоты дерева. Решение оптимизационных задач по методике безусловной вариационной оптимизации показало, что суммарное количество биомассы в лесах (то есть показатель AGB) достигает минимума при наличии обратной зависимости диаметра от высоты деревьев.