Исследование обтекания проницаемого тела по линейной динамической модели проницаемости методом крупных частиц

Full systematic results of investigation of flows around permeable bodies in all range of permeability are given in this article. Linear Davidov’s kinematics condition is used for boundary formulation of surface of permeable body. Calculations are realized with Large-Particles Method. Bifurcation points of transition from one flow topology to another are finded. The flat and axially symmetric flows were considered.

Первые исследования течений жидкости через пористую среду были проведены Н.Е. Жуковским [1]. Это направление затем было развито в работах С.А. Христиановича [2], П.Я. Полубариновой-Кочиной [3] и др. Для тонкого тела простейшая модель проницаемости впервые была предложена Х.А. Рахматулиным [4].

Течение за полупроницаемой поверхностью может иметь очень сложную структуру. До сих пор эти структуры практически не поддавались исследованию. Даже в простом случае течения вблизи лобовой поверхности обтекаемого тела при наличии вдува через эту поверхность, который в определенном смысле моделирует проницаемость, структура течения очень сложная: появляется висячий пограничный слой, при неравномерном вдуве образуются зоны возвратно-циркуляционного течения и т.п. При вдуве через кормовую поверхность, например, в случае частичного протекания потока через обтекаемое тело, структура потока за кормой ещё более сложная: зона возвратно-циркуляционного течения оттесняется от кормовой поверхности тела, смещаются точки отрыва и т.п. За плохообтекаемыми телами образуются срывные зоны возвратно-циркуляционного течения. Эти зоны являются замкнутыми, локализуются за кормой тела и отделяются контактной поверхностью от внешнего течения. Поток в зонах рециркуляционного течения обычно существенно дозвуковой, величины плотности и давления здесь также достаточно малы. Такие течения наблюдаются при обтекании парашютных систем, при фильтрации жидкостей и газов через проницаемые преграды во многих технических устройствах и технологических процессах.

Структуры сложных вихревых течений за кормой проницаемого тела зависят от степени проницаемости, от постановки граничных условий на поверхности тела. Получение точных численных результатов, адекватных реальным физическим процессам, во многом зависит от качества математической модели граничных условий. Ю.М. Давыдовым [5] была предложена иерархическая система физико-математических моделей проницаемости. Эти модели были реализованы при численном моделировании обтекания проницаемых тел методом крупных частиц [6, 7]. Физико-математические модели проницаемости состоят из двух классов: класса кинематических моделей и класса динамических моделей, они получили название "физико-математические модели проницаемости Давыдова" [8-12 и др.]. Достаточно подробные исследования обтекания проницаемого тонкого тела методом крупных частиц были проведены в работе [12].

При исследовании использовались по три варианта кинематических и динамических моделей проницаемости Давыдова.

Рассмотрим результаты расчетов обтекания полупроницаемой тонкой преграды с использованием линейной динамический модели проницаемости, которая имеет следующий вид:

Δ M _гр = k ₂₁ (p ₊- p _- ) , (1) где Δ М гр - расход массы через единицу поверхности проницаемой границы, k 21 -линейный динамический коэффициент проницаемости, р + , р - - значения давлений перед и за тонким телом, соответственно. Изменения значения коэффициента проницаемости k 21 находятся в диапазоне 0 ≤ k 21 ≤ 0,397х10^-2. Величина k 21 =0 соответствует непроницаемому телу ( Δ М =0), величина k 21 =0,397х10^-2 - полностью проницаемому. Исследовались как до -, так и сверхзвуковые режимы обтекания. В данной статье приводятся результаты по сверхзвуковому обтеканию с числом Маха набегающего потока М ∞ =2,0 для пространственно-двумерных плоского и осесимметричного случаев.

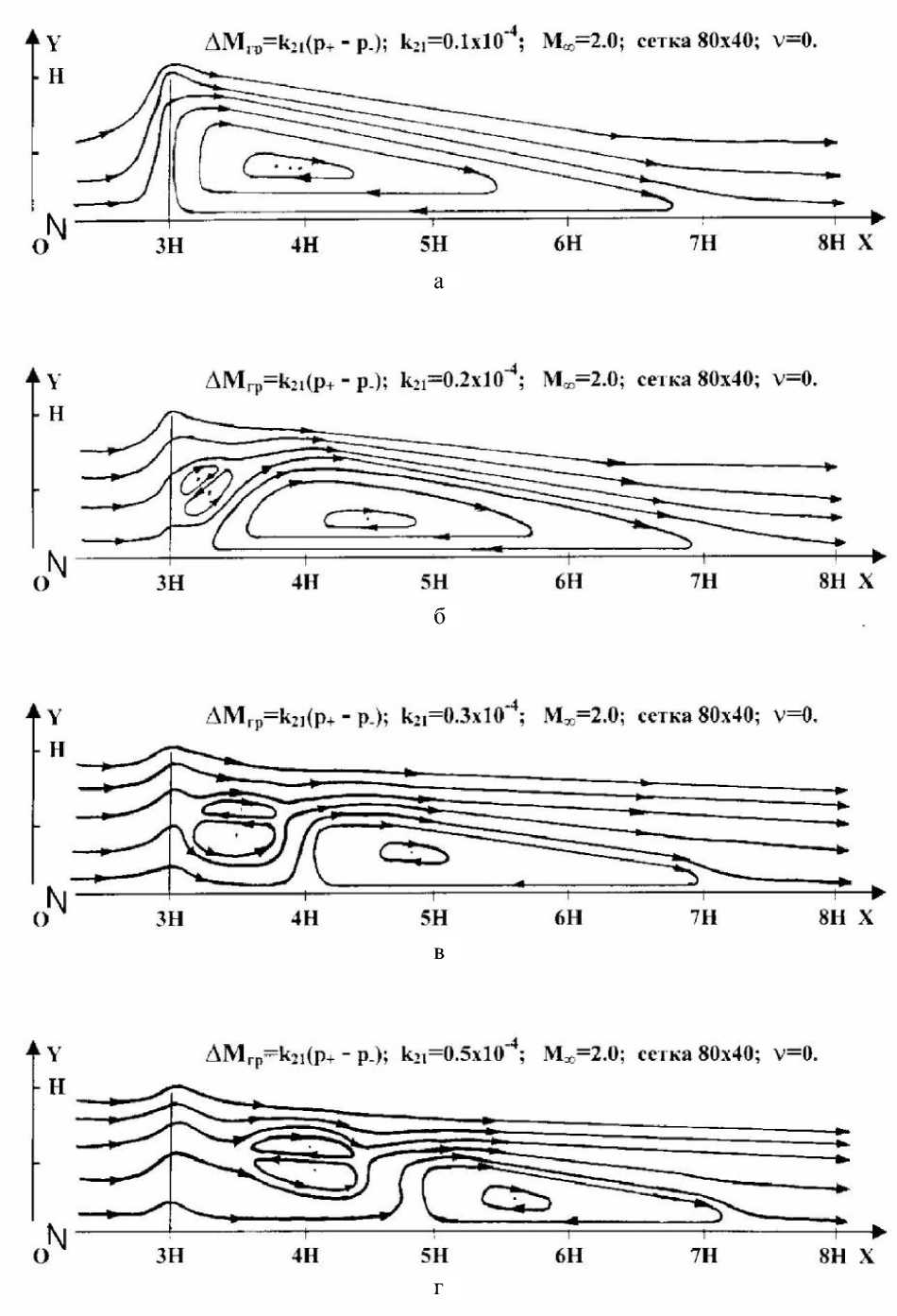
Покажем динамику изменения топологии течения в зависимости от величины коэффициента k 21 при применении модели (1). На всех рисунках использованы обозначения: v =0 соответствует плоскому случаю; v =1 - осесимметричному случаю. Результаты в плоском случае представлены на рис.1. При k 21 =0,1х10^-4 за пластинкой образуется обширная зона возвратно-циркуляционного течения с точкой отрыва, находящейся ниже верхней кромки проницаемой пластинки (см. рис.1,а). Дальнейшее увеличение коэффициента k 21 приводит к качественному изменению картины течения за проницаемой пластинкой. При k 21 =0,2х10^-4 основная возвратно-циркуляционная зона отходит на незначительное расстояние от кормы проницаемой пластинки. Кроме того, реализуется система двух небольших возвратноциркуляционных зон непосредственно за проницаемой пластинкой. Образуется также сквозная линия тока, проходящая между парой вихревых зон с замкнутыми линиями тока и основной возвратно-циркуляционной зоной (см. рис.1,б). При дальнейшем увеличении проницаемости (k 21 =0,3х10^-4, см. рис.1,в) происходит уменьшение основной возвратно-циркуляционной зоны и её удаление на расстояние ≈ 1Н (Н -высота пластины) от кормы проницаемой пластинки. Система пары вихревых зон с замкнутыми линиями тока смещается на небольшое расстояние от пластинки вправо и вверх; при этом горизонтальный размер этой двойной зоны вдоль плоскости симметрии увеличивается по сравнению со случаем k 21 =0,2х10^-4 (см. рис.1,б). При k 21 =0,3х10^-4 возрастает толщина слоя сквозного течения между парой зон и основной возвратноциркуляционной зоной (см. рис.1,в). Дальнейшие увеличение коэффициента k 21 до значения k 21 =0,7х10^-4 не приводит к качественному изменению картины течения; происходит количественное изменение размеров и места нахождения возвратноциркуляционных зон. Потоки, проходящие сквозь проницаемую пластинку, обтекая парные зоны возвратно-циркуляционного течения, сжимают их, уменьшая их толщину и, увлекая за собой, увеличивают их длину и протяженность сквозного потока. При этом возрастает расстояние между основной возвратно-циркуляционной зоной и обтекаемой пластинкой, а также уменьшается линейный размер основной приосевой зоны (см. рис.1,г-1,е). При достижении коэффициентом проницаемости k 21 величины k 21 =0,8х10^-4 (см. рис.1,ж) в картине течения происходит качественное изменение: исчезает основная возвратно-циркуляционная зона; парные вихревые зоны возвратноциркуляционного течения отходят дальше от кормы (см. рис.1ж),

tY

- Н

ДМгр=к21(р+ -

р_); кг^О.бхЮ"4; Мх=2.0; сетка 80x40; v=0.

►

8Н X

ДМгр=к2](р+ -

д

Р-); к2|=0.7х10"4; Ме=2.0; сетка 80x40; v=0.

8Н X

е

4 Y

■ II

ДМгр=к2|(р+- р.); к2|=0.8х10'4; М»=2.0; сетка 80x40; v=0.

п ►

8Н X

ж

t Y

- Н

ДМгр=ки(р+- р_); к2|=0.825х10'4; М»=2.0; сетка 80x40; v=0.

О        ЗН        4Н        511        6Н        7Н        8Н X

з

Рис.1. Изменение топологии течения в зависимости от величины коэффициента k 21 : (а) - k 2i = 0,1 х 10^-4 , (б) - k 2i = 0,2 х 10^-4 , (в) - k 2i = 0,3 х 10^-4 , (г) - k 2i = 0,5 х 10^-4 , (д) - k 21 = 0,6 х 10^-4, (е) - k 21 = 0,7 х 10^-4, (ж) - k 21 = 0,8 х 10^-4, (з) - k 21 = 0,825 х 10^-4

их линейные размеры становятся несколько меньше. При достижении коэффициентом проницаемости значения k 21 =0,825х10^-4 (см. рис.1,з) происходит переход от течения с возвратно-циркуляционными зонами к течению без зон с замкнутыми линиями тока. Дальнейшие увеличение k 21 до верхнего предельного значения соответствует безотрывному обтеканию с монотонным уменьшением сопротивления проницаемого тела и асимптотическим приближением к свободному невозмущённому течению.

Резюмируя описанные выше результаты численного эксперимента, отметим, что с использованием модели (1) в плоском случае при значениях коэффициента проницаемости k 21 в диапазоне 0 ≤ k 21 ≤ 0,8х10^-4 (см. рис.1,а-1,ж) реализуется обтекание с возвратно-циркуляционными зонами, а в диапазоне 0,825х10^-4 ≤ k 21 ≤ 0,397х10^-2 -безотрывное течение. Величины k 21 =0,2х10^-4 , k 21 =0,8х10^-4 , k 21 =0,825х10^-4 являются бифуркационными значениями линейного динамического коэффициента проницаемости.

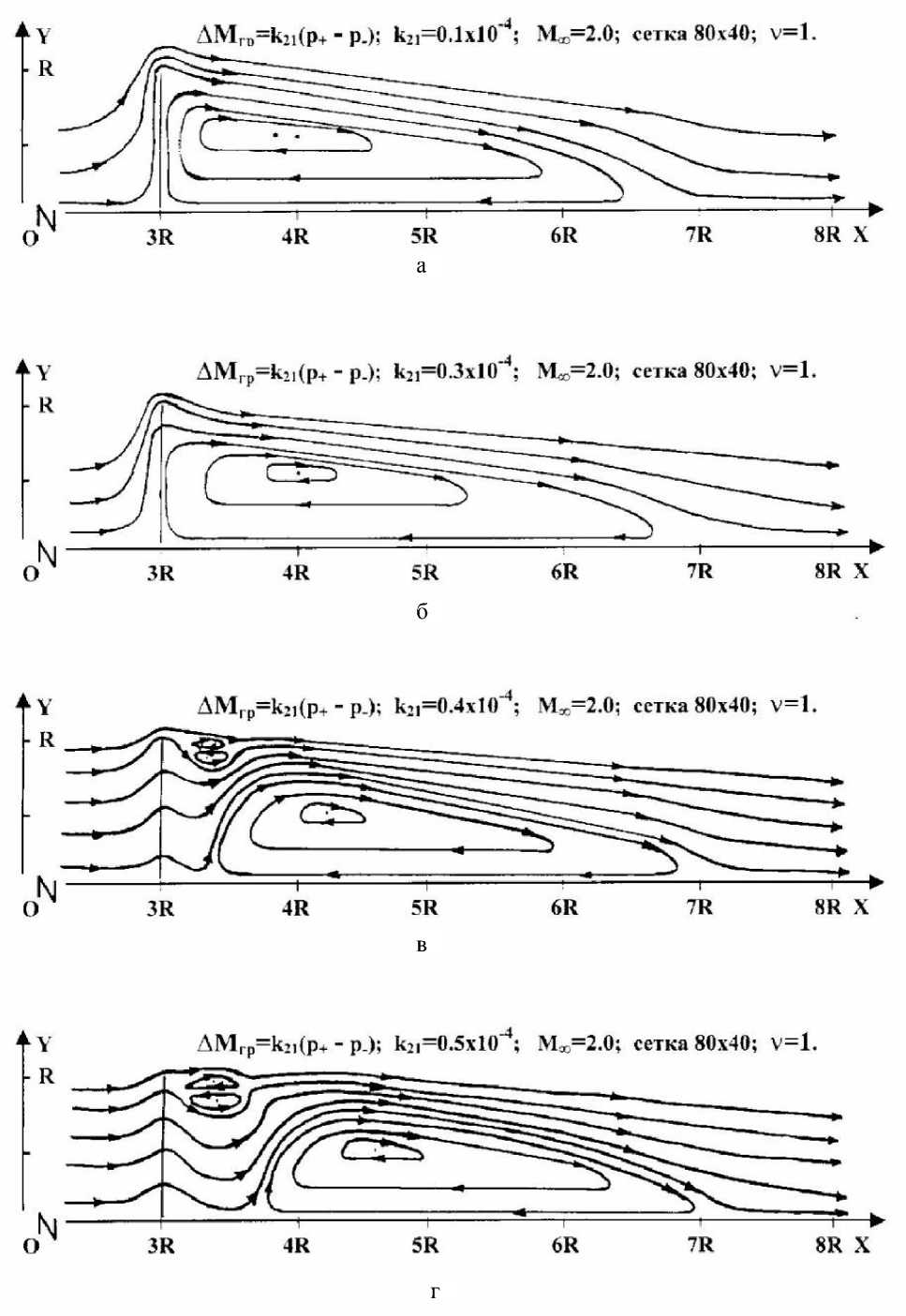
Для сравнения с результатами, полученными с использованием модели (1) в плоском случае, на рис.2 показаны линии тока в осесимметричном случае в зависимости от величины коэффициента проницаемости тонкого диска . На этом рисунке можно заметить качественные отличия осесимметричного случая от плоского (см. рис.1) в указанных диапазонах значений коэффициента проницаемости. При малых значениях k 21 (k 21 =0,1х10^-4, см. рис.2а; k 21 =0,3х10^-4, см. рис.2,б) существует примыкающая к корме проницаемого диска обширная зона возвратно-циркуляционного течения, при этом точки отрыва потока по мере увеличения коэффициента проницаемости смещаются ниже верхней кромки диска. При k 21 =0,4х10^-4 (см. рис.2,в) реализуется качественно новая картина течения: основная зона возвратно-циркуляционного течения отходит от кормы проницаемого диска на расстояние 0,35R (R - радиус диска) и её линейный размер уменьшается. В окрестности кормы образуется новая двойная вихревая зона возвратно-циркуляционного течения (двойной тороид), состоящая из двух вращающихся друг навстречу другу потоков с замкнутыми линиями тока и расположенная вблизи верхней кромки диска. Этот двойной тороид имеет небольшие линейные размеры. Дальнейшее увеличение коэффициента проницаемости k 21 до величины k 21 =0,1х10^-3 включительно не приводит к качественным изменениям структуры течения (см. рис.2,г-2,е), хотя количественные изменения в картине течения имеют место. Основная зона возвратно-циркуляционного течения уменьшается и дистанцируется от проницаемого диска; при этом сохраняется двойной тороид вблизи верхней кормы диска, его размеры могут незначительно изменяться (см. рис.2,в-2,е). При достижении коэффициентом проницаемости значения k 21 =0,125х10^-3 (см. рис.2,ж) двойной тороид вблизи верхней кромки диска исчезает; основная зона возвратноциркуляционного течения продолжает удаляться от кормы диска; её линейный размер при этом уменьшается. Дальнейшее незначительное увеличение коэффициента k 21 до величины k 21 =0,15х10^-3 (см. рис.2,з) приводит к новому качественному изменению структуры течения за проницаемым диском: происходит переход от возвратноциркуляционного течения к течению без зон с замкнутыми линиями тока. Величина коэффициента проницаемости k 21 =0,15х10^-3 при обтекании полупроницаемого диска в осесиммтричном случае является бифуркационным значением параметра. При дальнейшем увеличении коэффициента k 21 до верхнего предельного значения линейного динамического коэффициента проницаемости реализуется безотрывное обтекание. По мере увеличения коэффициента k 21 монотонно уменьшается сопротивление проницаемого диска; структура потока асимптотически приближается к свободному невозмущённому течению.

ДМгр=к21(р4 - p.); к^ЛхЮ"4; M«=2.0; сетка 80x40; v=L

5R

д

7R       8R X

4 Y

• R

ДМгр=к21(р+- р.); k2i=0.1xl0

сетка 80x40; v=l

=1--►

8R X

е

4y

- R

ДМгр=к2|(р4 - p.); k2i=0.125xl0"3; М«=2.0; сетка 80x40; V=l.

8R X

ж

ДМгр=к21(р+ - p.); k2i=0.150xl0 3; Mx=2.0; сетка 80x40; V=l.

N----------------------------------- I-------------------1---------------------I---------------------i-------------------- 1-----►

О        3R        4R       5R        6R        7R       8R X

з

Рис.2. Изменение топологии течения в зависимости от величины коэффициента k 21 : (а) - k 2i = 0,1 x 10^-4 , (б) - k 2i = 0,3 x 10^-4 , (в) - k 2i = 0,4 x 10^-4 , (г) - k 2i = 0,5 x 10^-4 , (д) - k 21 = 0,7 x 10^-4 , (е) - k 21 = 0,1 x 10^-3, (ж) - k 21 = 0,125 x 10^-3, (з) - k 21 = 0,15 x 10^-3

Результаты расчетов показывают, что в осесимметричном случае при использовании линейной динамической модели (1) в диапазоне величин коэффициента проницаемости k 21 0 ≤ k 21 ≤ 0,125х10^-3 (см. рис.2,а-2,ж) существует возвратноциркуляционное течение, а в диапазоне 0,15х10^-3 ≤ k 21 ≤ 0,397х10^-2 реализуется безотрывное течение. При значении k 21 =0,3х10^-4 в осесимметричном случае ещё существует присоединённая к корме зона возвратно-циркуляционного течения (см. рис.2,б). В плоском же случае при этом значении коэффициента проницаемости реализуется существенно более сложная картина течения, описанная выше (рис.1,в). Результаты расчетов показывают динамику изменения структуры течения в плоском и осесимметричном случаях в зависимости от величины коэффициента проницаемости при использовании линейной динамической модели для расчета обтекания тонкого полупроницаемого тела. При одинаковых значениях коэффициента k 21 разность давления перед и за тонким телом в плоском случае всегда больше, чем в осесимметричном случае. Это обстоятельство в рамках динамической модели приводит к разным структурам течения за проницаемым телом в плоском и осесимметричном случаях - к лучшему продуванию (пропусканию) газа через тело в случае большей разности давлений. Отсоединённая от кормы зона возвратно-циркуляционного течения в плоском случае наблюдается при значительно меньших значениях коэффициента проницаемости (k 21 =0,2х10^-4, см. рис.1,б) по сравнению с осесимметричным случаем (k 21 =0,4х10^-4, см. рис.2,в).