Исследование очесывающего аппарата устройства для уборки зерновых культур как колебательной системы

Одним из перспективных нетрадиционных способов уборки зерновых культур является уборка с использованием устройства, очесывающего растения на корню. Способ известен достаточно давно, но именно сейчас получает развитие. Жатки очесывающего типа к зерноуборочным комбайнам пока не получили широкого распространения, но уже выпускаются серийно в России и за рубежом [1–3].

Пропускную способность комбайна ограничивают соломотряс и очистка. Уменьшение подачи соломы оптимизирует процессы сепарации и очистки и создает предпосылки для увеличения производительности зерноуборочного комбайна [4]. Высокое содержание свободного зерна в очесанном ворохе дает предпосылки для создания перспективных малогабаритных прицепных очесывающих устройств для уборки зерновых [5; 6].

Основной проблемой, которую необходимо решать при разработке, являются потери зерна неочесом. Для снижения потерь мы предлагаем конструкцию очесывающего аппарата с виброприводами (рис. 1) [7].

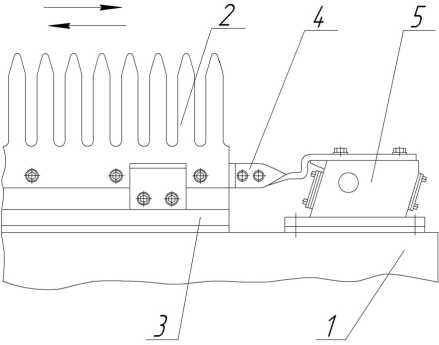
Р и с. 1. Очесывающий аппарат с вибрационным возвратно-поступательным движением гребенок

F i g. 1. Stripping device with vibrating reciprocating motion of stripping fingers

Данное устройство совмещает очес зерновых культур и вибрационное воздействие гребенок на колос растений. Основными составляющими очесывающего аппарата являются барабан 1 с кронштейнами 3 , гребенки 2 , виброприводы 5 . Кронштейны 4 соединяют гребенки, собранные на брусьях, с виброприводами 5 .

В процессе захвата растений и очеса колосьев гребенки в направляющих совершают вибрационные возвратно-поступательные движения с определенной частотой и амплитудой. Колебательные движения облегчают внедрение гребенок в стеблестой. Кроме того, колосья растений воспринимают вибрационное воздействие гребенок, что способствует более полному выделению зерна из колоса.

Определение и оптимизация параметров рабочего процесса очеса зерновых культур предполагают создание математической модели процесса. Важнейшим этапом математического описания данного колебательного процесса является составление дифференциального уравнения движения гребенки.

Цель исследования – составление расчетной схемы и дифференциального уравнения движения очесывающей гребенки, совершающей вибрационные возвратно-поступательные движения.

Обзор литературы

Прочность связи зерна с колосом неравномерна по длине колоса. Менее прочно связаны с колосом зерна, расположенные в средней части. Данные факторы обуславливают потери зерна неочесом при работе очесывающих устройств. В одной из работ приведены данные по общим потерям зерна и потерям неочесом при использовании адаптеров различной конструкции [8]. Так, после внедрения адаптера фирмы Shelbourne Reynolds потери зерна неочесом изменялись в диапазоне 0,32–0,97 %. При этом они возрастали пропорционально скорости комбайна. Потери неочесом на хлебах с полегло-стью 80 % достигали 3,15 %. Необходимо также отметить данные по потерям зерна в оборванных колосьях при работе адаптера конструкции ЦНИИМЭСХ, разработанного совместно с ФГБНУ «Федеральный научный агроинже-нерный центр ВИМ». Указанные потери зерна изменялись в пределах 0,40–4,52 %.

В другой работе приведены результаты экспериментальных исследований при уборке овса и пшеницы методом очеса. При этом отмечено, что рабочая скорость комбайна при уборке овса выше, чем при уборке пшеницы. Это зависит от более прочной связи зерна пшеницы с колосом. В то же время отмечена более прочная связь метелки овса со стеблем, чем колоса пшеницы с растением [9].

В результате анализа указанных исследований можно отметить важность снижения усилия очеса растений и улучшение процесса отделения зерен от колосьев. Это дает предпосылки не только для снижения потерь неочесом, но и для снижения потерь зерна в оборванных колосьях, так как основной причиной данного процесса остается превышение усилия отделения зерна над обрывом колоса. Использование очесывающего аппарата с виброприводами позволит снизить указанные потери.

Был произведен обзор литературных источников, посвященных использованию вибропроводов в промышленности, на путевых машинах. Кроме того, рассмотрены методики описания движения механических систем в рамках теории колебаний.

Рассмотрены конструктивные особенности и режимы работы вибрационных машин. Отмечено, что виброприводы современных транспортирующих механизмов и машин выдают прямолинейные гармонические колебания [10].

Основными рабочими органами путевых выправочно-подбивочно-рих-товочных машин являются подбивоч-ные блоки. Подбойки подбивочных блоков внедряются в балласт и производят его обжатие. Подбойки колеблются с частотой 35 Гц. Это упрощает их внедрение в балласт и придает ему подвижность, необходимую для уплотнения [11]. Гидропривод машины обеспечивает вращение эксцентрикового вибровала, движение кривошипного механизма и, соответственно, вибрацию подбоек.

Том 31, № 3. 2021

Анализируется проблема избыточного вибровоздействия, приводящего, в том числе, и к разрушению балласта [12].

Автор следующей статьи вводит понятие «время вибровоздействия» применительно к путевым машинам и балласту. Отмечено, что увеличение времени вибровоздействия является резервом повышения качества подбивки балласта. Отмечена зависимость величины передаваемой энергии от частоты вибрации. Значительно возрастает передаваемая на балласт энергия при переходе от частоты вибровоздействий в 45 Гц к частоте в 35 Гц [13].

Другая статья посвящена проблематике резания полимерных композиционных материалов. Такие материалы обладают специфической структурой, а также анизотропией свойств, значительно усложняющих их механическую обработку. Можно добиться значительного повышения качества обработки и снижения сил резания (до 80 %), используя комбинацию традиционного сверления и вибрационного воздействия на заготовку в ультразвуковом диапазоне. Одним из факторов, обеспечивающих указанные эффекты, является значительное улучшение процесса стружкообразования [14].

Аналогичный прием предложен для обработки глинозема. Указывается, что ротационная ультразвуковая обработка – один из наиболее эффективных методов для хрупких материалов. Также отмечены снижение силы резания и негативное влияние на процесс резания боковой вибрации. Предложена методика ее минимизации [15].

Положения рассмотренных выше работ [14; 15] позволяют предложить гипотезу о снижении сил очеса растений при использовании очесывающего аппарата с виброприводами.

Исследованы усилия очеса при использовании аппарата традиционной конструкции [16]. Вопросы прочности связи зерна с колосом рассмотрены в другой работе [17]. Подтверждение или опровержение предложенной гипотезы в теоретической плоскости возможно только при подробном математическом описании колебательного процесса очеса.

Авторы анализируют преимущества и конструктивные особенности бесшатунных механизмов преобразования движения. Составлена кинематическая схема, получены основные уравнения кинематики и динамики механизма, а также предложена методика определения степени влияния параметров системы на кинематические и динамические характеристики механизма. При этом отмечена необходимость уравновешивания сил инерции и их моментов [18].

Рассмотрены особенности математического описания колебательных процессов под действием внешних сил. Внимание уделено методологии определения и представления механической мощности и ее составляющих. Инерционная мощность отмечена как характерная для вибромашин. Проведена аналогия между механическими и электрическими составляющими мощности [19].

Материалы и методы

Важнейшим этапом построения расчетной схемы является определение числа степеней свободы системы. Так как гребенка движется в направляющих, ограничивающих ее продольное перемещение, она работает только в поперечном направлении. Данная система может рассматриваться как имеющая одну степень свободы.

Предложенная расчетно-графическая схема колебательной системы представлена на рисунке 2. После выбора расчетной схемы составим уравнения движения системы.

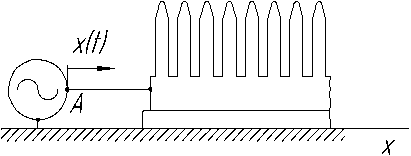
Р и с. 2. Расчетно-графическая схема колебательной системы

F i g. 2. Calculation and graphic diagram of an vibrating system

Наиболее общим является метод, предполагающий использование уравнения Лагранжа II рода. Оно является дифференциальным уравнением второго порядка:

• 8 T 8x

  |- — ₌ Q П ₊ Q Ф ₊ Q B ,  (1)

  ) 8x

  
  

  4 I dt (

  
  

где Т - кинетическая энергия колебательной системы; x - обобщенная координата колебательной системы; Q ^П – обобщенная сила потенциальных сил; Q ^Ф – обобщенная сила от действия сил сопротивления; Q ^В – обобщенная сила от возмущающих сил.

Рассматриваемая система совершает вынужденные колебания. В данном случае они вызываются не заданными силами, а возникают благодаря приведению в движение по заданному закону точки системы, то есть точки на гребенке. Такое возбуждение будет являться кинематическим. При этом задачу о кинематическом возбуждении нетрудно свести к задаче о силовом возмущении. На данном этапе составления расчетной схемы пренебрегаем силами трения и силами сопротивления, связанными с воздействием на колос.

При составлении уравнения Лагранжа на первом этапе вычисляем кинетическую энергию системы.

Результаты исследования

Запишем выражение для кинетической энергии гребенки:

mV 2   1

T =---= - mx2

22,

где m – масса гребенки, V – скорость гребенки.

Имеем:

движения гребенки будет иным. Расчетно-графическая схема для данного случая представлена на рисунке 3. При составлении расчетной модели учтем силы сопротивления при движении гребенки и очесе зерновых культур.

5 T

— = mx ; 5 x

--0; d; ax      dt

a t

• *

■     = mx.

ax

Так как выходное звено вибратора совершает гармонические колебания, то

x = x 0sin(«t + 3),       (3)

где to - угловая частота колебаний выходного звена вибропривода; 3 - начальная фаза колебаний.

В этом случае

mx = mx0to2 sin(^/ + 5).    (4)

В данном уравнении роль обобщенной силы выполняет величина mx _ооу sin( «Z + 5 ) .

Перепишем уравнение (4) в следующем виде:

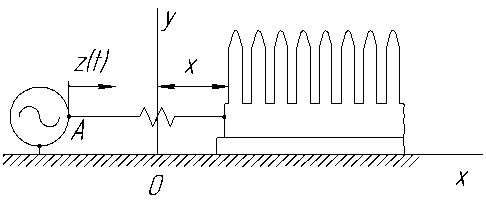
Р и с. 3. Расчетно-графическая схема колебательной системы с упругим элементом

F i g. 3. Calculation and graphic diagram of an vibrating system with an elastic element

Составим уравнение Лагранжа для гребенки относительно подвижной системы отсчета Оxy , начало которой движется вместе с точкой А так, что ОА при движении остается постоянным.

В данном случае в уравнении (1) появляется обобщенная сила потенциальных сил Q ^П:

где

mx = H sin(«Z + 5),     (5)

Q ^п

ап

— = - cx, аx

H = mx 0to2.

В уравнении (6) H – постоянная, характеризующая обобщенную силу и являющаяся ее амплитудой.

Как видно из уравнения (6), в нашем случае при кинематическом возбуждении заданием движения x = x 0 sin( ®/ + 5 ) гребенки H пропорционально ω ².

Уравнение (5) будет являться дифференциальным уравнением движения гребенки, совершающей вибрационные возвратно-поступательные движения.

Если рассматривать кронштейн 4 (рис. 1) как упругий элемент, уравнение

где П - потенциальная энергия системы; с - коэффициент жесткости упругого элемента.

Силу сопротивления запишем следующим образом:

Q ^ф

д Ф ”Х55с

= - ^х,

где Ф - обобщенная сила сил сопротивления при движении гребенки и очесе; μ – коэффициент сопротивления.

Движение гребенки в данном случае будем рассматривать как сложное, состоящее из переносного вместе с точкой A и относительного по отношению к подвижной системе координат Оxy .

Кинетическая энергия гребенки в данном случае будет равна:

mV2     ( x + .

T =    = m

.

Для производных от кинетической энергии имеем:

— - 0; — = m ( x + z ) ;

ax     8x d 8 T ---= m dt 8x

Подставляя полученные выражения в уравнение (1), получим:

m (x + z) = - cx - ЦХ или mx + px + cx --mz.    (10)

В данном уравнении роль обобщенной силы выполняет величина - mz .

С учетом (3) уравнение (10) примет вид:

mx + ^х + cx = mz ₀ го ²sin( rot + § ). (11)

Уравнение (11) и будет являться дифференциальным уравнением движения гребенки при наличии упругого элемента.

Выделим постоянную H , характеризующую обобщенную силу, по аналогии с уравнением (5):

H = mz ₀ ro 2 .         (12)

Здесь величина H , так же как и в уравнении (6), пропорциональна ω ².

Тогда mx + цх + cx = H sin(rot + §). (13)

Для приведения уравнения (13) к стандартному виду разделим обе части на m и введем обозначения k = c ;

h = - ; n = ^.

mm

Дифференциальное уравнение вынужденных колебаний в окончательной форме будет иметь следующий вид:

x + nx + kx = h sin(wZ + 5). (14)

Для решения дифференциального уравнения (14) воспользуемся пакетом прикладных программ MATLAB.

Аналитическая запись решения будет иметь следующий вид:

-05 1 ( ⁿ - ( n -4 k ) x = C 1 e   ^{2 2}      '

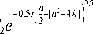
• -°,⁵ t [ П + ( n ² -4 к j )     0,5 1 ( n 2 - 4 k j ^0,5 _nt

he ^{2 2}       ' e '    ' + U,

2 ¹

n ² ( n ² - 4 k j ^0,5 - 4 kn - 2 k ( n ² - 4 k j ^0,5 + 2 m ² ( n ² - 4 k j ^0,5 + n ³

• -0,5 1 ( n - ( n 2 -4 k 1Г nt - 051 ( n - ( n -4 k VT

________________he 121 j) e2 121     'i U2________________ n21 n2 - 4 kj0-5 + 4 kn-2 k (n2 - 4 k ^°’5 + 2m2 (n2 - 4 kj0-5 - n3

где

U1 = sin(^/ + 5)(n2 - 4k)0,5 -- 2ro cos(rot + 5) + n sin(^/ + 5),

U2 = sin(^/ + 5)(n2 - 4k)0,5 + + 2® cos(rot + 6) - n sin(^/ + 5).

Вид кривой колебаний будет зависеть от соотношения k и ω . При близких значениях √ k и ω имеет место случай резонанса, то есть совпадение частот собственных колебаний и возмущающей сил. Наличие сопротивления определяет следующую особенность протекания резонансных явлений: амплитуда колебаний остается постоянной, а не изменяется с течением времени.

Вынужденные колебания очесывающей гребенки при √k ≠ ω будут являться гармоническими колебаниями с постоянной амплитудой. Частота колебаний гребенки будет совпадать с частотой возмущающей силы или, применительно к нашему случаю, с частотой колебания выходного звена вибропривода.

Обсуждение и заключение

Предложена расчетная модель для описания движения гребенок очесывающего аппарата с виброприводом. Получено уравнение движения гребенки, совершающей вибрационные возвратно-поступательные движения.

Предложено в расчетной схеме выделить упругий элемент и получить более общий случай движения очесывающей гребенки и, соответственно, более общее математическое описание данного движения. Движение гребенки в данном случае рассмотрено как сложное. Характерной особенностью математического описания является наличие обобщенной силы потенциальных сил и обобщенной силы от действия сил сопротивления. Получено дифференциальное уравнение движения гребенки при наличии упругого элемента, а также решение данного уравнения.

При отсутствии резонансных явлений вынужденные колебания очесывающей гребенки будут являться гармоническими с постоянной амплитудой и частотой, равной частоте колебания выходного звена вибропривода.

Отмечено, что при близких значениях V к и го имеет место случай резонанса, то есть возрастание амплитуды до величин, несоразмерных с амплитудой синусоидальной силы, вызывающей само колебание системы. Параметры системы необходимо выбирать таким образом, чтобы избежать этого негативного, в данном случае, явления.

Поступила 06.02.2021; одобрена после рецензирования 10.03.2021; принята к публикации 20.03.2021

Автор прочитал и одобрил окончательный вариант рукописи.