ИССЛЕДОВАНИЕ ОПТИЧЕСКИХ ПОВЕРХНОСТЕЙ ПЛОСКОВЫПУКЛЫХ ЛИНЗ ЭКСПЕРИМЕНТАЛЬНОЙ ИНТЕРФЕРЕНЦИОННОЙ УСТАНОВКОЙ С ДИФРАГИРОВАННЫМ ОПОРНЫМ ВОЛНОВЫМ ФРОНТОМ

В настоящее время огромное внимание уделяется методам и средствам оптических измерений в процессе разработки оптических и оптико-электронных приборов и комплексов [1, 2]. Эти методы и средства играют важнейшую роль в осуществлении контроля оптических деталей. Их высокая точность и чувствительность обеспечивают достоверность измерений исследуемых объектов [3, 4]. Пороговая чувствительность и точность методов оптических измерений находится в диапазоне от 1 мкм до 0.01 мкм [5, 6]. Используя оптические приборы и системы совместно с современными компьютерными технологиями возможно увеличить эти параметры в десятки раз. Анализ научно-технической литературы показал, что оптический контроль доказал свою достоверность, информативность, наглядность и надежность [7, 8]. Поэтому оптические методы и средства нашли свое применение в естественнонаучных и научно-технических направлениях. С каждым днем их роль возрастает в технической, медицинской, биологической и химической практиках [9, 10].

Среди методов оптического контроля преимущественно выделяются методы когерентной оптики, а именно интерференционные методы [11, 12]. Интерференционные методы позволяют решать задачи различной сложности: исследовать плоские, сферические и клиновидные поверхности оптических элементов; получать информацию о деформации объектов со сложным рельефом поверхности [13, 14]. Важность интерференционных методов обусловлена их возможностями. Эти методы дают возможность получать информацию о статистических и динамических процессах, данные о волновых фронтах в разные промежутки времени, информацию о поверхности объекта в качественном и количественном аспектах, изображения в трехмерной графике [15, 16].

Интерференционные методы контроля оптической поверхности и работа соответствующих приборов основаны на анализе светового излучения, отраженного от исследуемой поверхности [17, 18]. Оптические поверхности изделий представляют собой формы сфер, плоскостей, наклонных плоскостей. Изучение научно-технической литературы представило следующую картину: при измерениях оптических поверхностей возможно применять теневой метод Фуко, метод Гартмана, а также интерферометрический метод с использованием интерферометра Физо [19, 20].

В последние годы появились научные работы, направленные на получение количественных оценок ошибок системы по данным испытаний теневым методом, а в методе Гартмана научились обеспечивать наглядность и по гартманограммам в аберрационно-корригированной оптической системе извлекать величину аберраций. Касаемо интерференционного метода, то до сих пор контроль оптической поверхности осуществляется интерферометром Физо, т.к. в нем снижена чувствительность к вибрациям, которая имелась у двухлучевого интерферометра Тваймана [2, 21]. И еще важная деталь: выпускаемые оптико-электронные комплексы, имеющие в составе интерферометр Физо, оснащены компьютерами, видеовыходом и дорогостоящим программным обеспечением. Однако их точностные возможности ограничены необходимостью применения в их конструкции образцовых деталей, точность которых неизбежно ограничена и находится на уровне λ/20 [2, 22].

Схемные решения классических интерферометров основаны на формировании опорного волнового фронта с применением образцовых оптических поверхностей (интерферометры Тваймана и Физо), которые до сих пор широко используются для контроля оптических поверхностей. На сегодняшний день наблюдается рост тенденции контроля элементов оптических систем наивысшего класса точности. К таким оптическим элементам изделий можно отнести оптические элементы современных исследовательских микроскопов, технологической аппаратуры микроэлектроники и оптико-электронных устройств записи информации [23, 24]. Требования к точности расчета и выполнения этих систем находятся на уровне 1/20– 1/30 λ, где λ — длина волны оптического излучения. Таким образом, для контроля при их изготовлении и применении необходимы приборы, обеспечивающие точность на уровне 1/100–1/200 λ, т.е. на порядок точнее классических [2, 25].

Поэтому может представлять интерес исследование оптических поверхностей плосковыпуклых линз, применяемых в объективах современных интерференционных микроскопов, интерференционной установкой с дифрагированным опорным волновым фронтом.

Цель работы состояла в исследовании оптических поверхностей плосковыпуклых линз экспериментальной интерференционной установкой с дифрагированным опорным волновым фронтом.

ПОСТАНОВКА ЗАДАЧИ

В современных интерференционных микроскопах микрообъективы являются одними из основ- ных элементов. Плосковыпуклые линзы используются в этих микрообъективах, и от того, какое качество поверхности линзы, зависит точность измерений. В последние 10–12 лет микрообъективы создавались на базе импортных оптических элементов (двояковыпуклых, двояковогнутых, плосковыпуклых линз, плоскопараллельных пластин и т.д.). Поэтому необходимо было провести измерения оптических поверхностей плосковыпуклых линз отечественного производства в рамках импортозамещения, предоставленных ООО "Завод Оптических Изделий". Измерения проводились на экспериментальной оптико-измерительной установке, построенной на базе лазерного дифракционного интерферометра.

ОБЪЕКТ И МЕТОД ИССЛЕДОВАНИЙ

Исследовались три вида плосковыпуклых линз: из бесцветного оптического стекла марки К8, кварцевого стекла марки КИ (плавленый кварц SiO 2 ) и селенида цинка (ZnSe). Все образцы имели одинаковые геометрические размеры: диаметр 10 мм, толщина по оси 3 мм, толщина кромки 2 мм.

Для контроля оптических поверхностей изделий различных форм используют автоматизированные комплексы и приборы, построенные на базе интерферометра Тваймана или Физо [2, 20, 25]. Последняя технология проста в использовании и имеет малую виброустойчивость. Данные приборы и комплексы имеют один значимый недостаток — неустранимые остаточные ошибки опорного волнового фронта эталона, которые возникают при его изготовлении. Автоматизированные интерферометрические комплексы, построенные по классической схеме, работа которых основана на анализе светового излучения, отраженного от контролируемой поверхности, и по сей день применяются на различных оптических производствах. В повседневной практике в результате длительной эксплуатации этих комплексов возникали проблемы с измерениями. Например, при контроле одного и того же образца в одно время были одни параметры, а в другое время — отличные от предыдущих параметров. Видимо, это связано с ненадлежащим хранением эталона, да и сами комплексы 1973 г. выпуска.

В настоящее время созданы и активно разрабатываются современные автоматизированные интерферометрические комплексы на базе лазерного интерферометра с дифрагированным опорным (эталонным) волновым фронтом [2, 25]. Преимущества такой схемной реализации над классической в том, что дает экспериментатору удобство и комфорт при эксплуатации такого комплекса, простоту в управлении. В таком схемном решении физический эталонный образец заменен на дифрагированный эталонный волновой фронт, а значит, что точность измерений вырастает в разы. Снимается вопрос об остаточных ошибках опорного волнового фронта эталона и его ограничении точности при изготовлении.

Поэтому для контроля оптических поверхностей элементов высокоточных оптических приборов и комплексов целесообразно применять лазерную интерференционную экспериментальную установку с дифрагированным эталонным волновым фронтом.

В Приложении показан внешний вид установки. Излучение от лазера имеет высокую когерентность и способно фокусироваться в диаметры от 1 мкм до 10 мкм. В экспериментальной установке в качестве эталона использовался сферический волновой фронт, образованный дифракцией сходящихся лучей на отверстии с диаметром, равным 5 мкм. Точечная диафрагма выполнена из полированной металлической пластинки с диаметром отверстия 5 мкм. Отверстие служило источником дифракционной волны. Сложение этой волны (опорной) с волной, отраженной от измеряемой поверхности (объектной), есть результат интерференции.

На рис. 1 представлена оптическая схема лазерной интерференционной установки с дифрагированным эталонным волновым фронтом.

Свет от когерентного источника 1 (ЛГ-79-1 — He-Ne лазер с λ = 0.63 мкм, P = 15 мВт), пройдя отрицательный компонент 2, фокусируется объективом 3 в точечное отверстие 5 наклонной высокополированной металлической пластинки 4. Отверстие совмещено с центром сферической поверхности исследуемого объекта 13. В ветви наблюдения имеются объектив 9 и окуляр 11 для наблюдения освещенной точечной диафрагмы и автоколлимационного изображения точки в центре контролируемой поверхности. Для наблюдения интерференции в зрачке дополнительно вводится линза Бертрана 10. Для регистрации интерферограммы за окуляром устанавливается камера 12.

Технико-эксплуатационные характеристики экспериментальной установки:

• •    предельная инструментальная погрешность — λ /100;

• •    апертура проверяемых поверхностей не более — 0.25;

• •    числовая апертура объектива —0.2;

• •    пределы перемещения интерференционной головки по 3 осям, мм —

• •    приемник изображения — фотокамера "Canon";

• •    источник света —             лазер ЛГ-79-1;

• •    длина волны излучения, мкм —0.63;

• •    габаритные размеры, мм —     750×450×550.

  

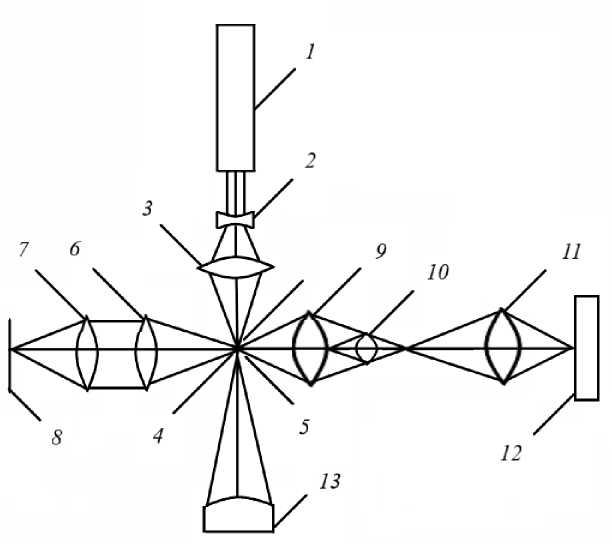
  Рис. 1. Оптическая схема лазерной интерференционной установки с дифрагированным эталонным волновым фронтом.

  1 — лазер; 2 — двояковогнутая линза; 3 — микрообъектив; 4 — высокополированная металлическая пластинка; 5 — точечное отверстие; 6 и 7 — встречные коллиматорные объективы; 8 — опорное зеркало; 9 — объектив; 10 — линза Бертрана; 11 — окуляр; 12 — фотокамера

  
  

ЭКСПЕРИМЕНТАЛЬНЫЕ РЕЗУЛЬТАТЫ

На экспериментальной установке были получены поочередно интерферограммы поверхностей исследуемых плосковыпуклых линз: из бесцветного оптического стекла марки К8, кварцевого стекла марки КИ (плавленый кварц SiO 2 ) и селенида цинка (ZnSe). Интерферограммы получены на дифракционном интерферометре, где в качестве эталонного волнового фронта используется волна, дифрагированная на отверстии с диаметром, равным 5 мкм. На рис. 2 приведены экспериментальные результаты. С целью восстановления фазы волнового фронта и топографии поверхности использовалась компьютерная программа обработки интерферограмм ZEBRA MathOPTIX.

Программа ZEBRA MathOPTIX аналогична программному обеспечению интерферометров таких ведущих фирм, как Zygo, Veeco и Möller-Wedel. Обработка интерферограмм производится в несколько этапов. Этап неглубокой пространственной фильтрации для удаления "мусора" из интерферограммы и этап идентификации полос — расстановка точек вдоль полос с определением возможного порядка базиса аппроксимации контролируемого волнового фронта или поверхности. Дальнейшая обработка основывается на серии математических методов интерпретации функций, целью которых является получение достоверного разложения отклонения волнового фронта или по- верхности по полиномам Цернике. При этом определяются такие важные величины, как размах (peak-to-valley, R) и среднеквадратическое отклонение (RMS, σ) в микрометрах.

Полученные результаты:

– Для оптического стекла марки К8:

R = 0.191180 мкм, σ = 0.03025 мкм.

– Для кварцевого стекла марки КИ:

R = 0.152534 мкм, σ = 0.02925 мкм.

– Для селенида цинка:

R = 0.102198 мкм, σ = 0.02113 мкм.

Выпуклые поверхности плосковыпуклых линз контролировались экспериментальной установкой с точностью не хуже 0.01 λ.

Исследования показали, что измеряемые оптические поверхности высокого качества. Использование этих оптических элементов в объективах интерференционных микроскопов целесообразно.

На представленной экспериментальной установке проведены измерения отражательной способности исследуемых поверхностей (экспериментальная установка позволяла получить данные об отражательной способности исследуемых образцов). Для проведения этих измерений использовались программы Golden Softwear Interferometer. Эти программы позволяли получать данные о зависимости коэффициента отражения от перемещения исследуемого образца по координатам x и y .

Рис. 2. Интерферограммы оптических поверхностей плосковыпуклых линз. а — линза из марки К8; б — линза из марки КИ; в — линза из ZnSe

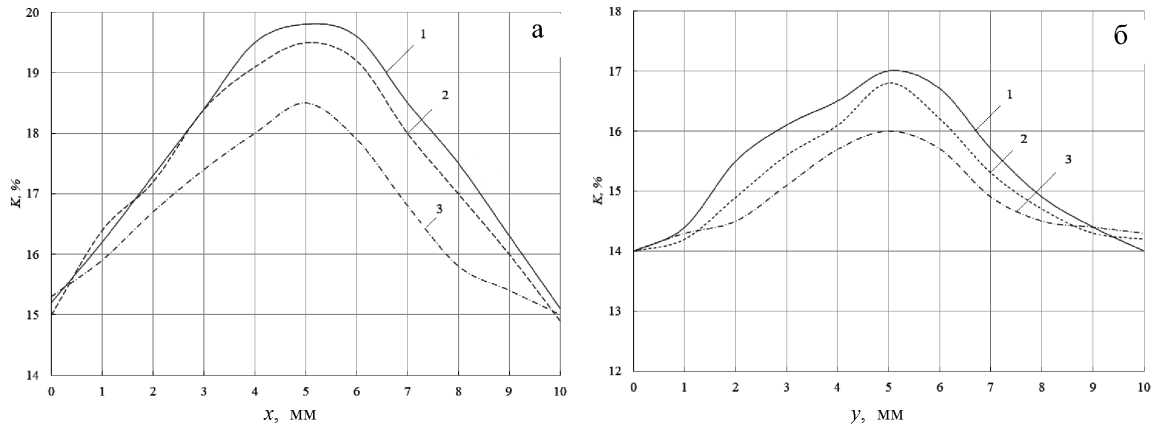
Рис. 3. Зависимость коэффициента отражения от перемещения исследуемых образцов.

а — по координате x для 1 — линзы из марки К8, 2 — линзы из марки КИ, 3 — линзы из ZnSe;

б — по координате y для 1 — линзы из марки К8, 2 — линзы из марки КИ, 3 — линзы из ZnSe

На рис. 3 представлены экспериментальные данные. Графические зависимости показывают, что распределение коэффициента отражения имело плавную колоколообразную форму, ни смещений, ни всплесков не наблюдалось. А это означает, что оптические поверхности высокого качества.

ЗАКЛЮЧЕНИЕ

Полученные экспериментальные результаты измерений оптических поверхностей исследуемых образцов значимы, т.к. данные оптические элементы планируется применить в объективах высокоточных оптических комплексов и приборов различного назначения. Данная работа представляет интерес как для оптического приборостроения, так и для совершенствования научной базы научных исследований оптических деталей различного назначения.

ПРИЛОЖЕНИЕ

Внешний вид экспериментальной установки