Исследование оптико-механических характеристик волокна в условиях термоцикла
Автор: Сметанников Олег Юрьевич, Труфанов Александр Николаевич, Лесникова Юлия Игоревна
Журнал: Известия Самарского научного центра Российской академии наук @izvestiya-ssc
Рубрика: Машиностроение и машиноведение
Статья в выпуске: 6-2 т.20, 2018 года.
Бесплатный доступ
В работе методами математического моделирования описана эволюция напряженно деформированного состояния в анизотропном оптическом волокне типа Panda в условиях контактного взаимодействия волокна и катушки при однорядной силовой намотке и циклическом изменении температуры. Методом конечных элементов построен конечномерный дискретный аналог. Выполнены многовариантные вычислительные эксперименты, в которых варьировались диаметр катушки и отклонения геометрии поперечного сечения волокна типа Panda. Получены зависимости описывающие эволюции напряженно-деформированного состояния в волокне, показателя преломления и двулучепреломления в светопроводящей жиле. Исследовано влияние отклонений геометрии поперечного сечения волокна типа Panda на оптические характеристики. Установлено, что для катушек малого диаметра характерно нелинейное изменение исследуемых параметров при высоких температурах, что связано с релаксационными процессами в защитно-упрочняющем покрытии волокна.
Анизотропное волокно, численное моделирование, полимерное защитно-упрочняющее покрытие, контактное воздействие, релаксация
Короткий адрес: https://sciup.org/148314122
IDR: 148314122 | УДК: 681.7.068
Текст научной статьи Исследование оптико-механических характеристик волокна в условиях термоцикла
В качестве чувствительных элементов некоторых современных датчиков физических величин используются специальные типы оптических волокон, изготовленных из легированных кварцевых стекол [1-3]. Для защиты световода от внешней среды и механических воздействий используют полимерные покрытия. В одном из вариантов исполнения такого защитно-упрочняю-щего покрытия (ЗУП) на волокно наносят два слоя УФ-отверждаемого полимера (рис.1). Внутренний слой покрытия при комнатной температуре находится в высокоэластическом релаксационном состоянии, его задача уменьшить влияние силовых воздействий (изгиб, поперечная сила и др.) на оптоволокно. Для защиты относительно мягкого первичного покрытия от механических воздействий и влияния внешней среды наносят второй слой, который при комнатной температуре находится в стеклообразном состоянии.
К специальным оптическим волокнам, используемым в составе различных измерительных
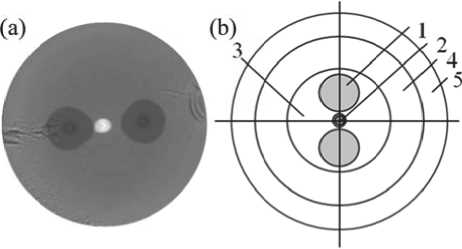
Рис. 1. Поперечное сечение анизотропного оптического волокна типа Panda.
(a) Фото и (b) cхема: 1 – силовой элемент, 2 – светопроводящая жила, 3 – основной материал (кварцевое стекло), 4 - внутренний ЗУП,
5 - внешний ЗУП комплексов, систем навигации на основе оптоволоконных гироскопов, систем мониторинга состояния строительных конструкций и др., предъявляются жесткие требования по корректной работе изделий в заданном эксплуатационном диапазоне температур. Перечислим основные факторы, влияющие на оптические характеристики волокна в условиях нарушения термостатики.
Главный вклад в изменение поляризации светопроводящей жилы при колебаниях температуры вносит гетерогенность кварцевой части волокна (сочетание отличающихся КЛТР с приблизительно одинаковыми упругими свойствами).
Второй по значимости фактор – существенное отличия КЛТР материалов ЗУП и кварцевого стекла. Несмотря на большую податливость внутреннего слоя ЗУП, в стесненных условиях он способен передавать заметные дополнительные температурные напряжения на светопроводящую жилу.
Помимо термоупругих напряжений и деформаций необходимо также учитывать вязкоупругие эффекты, связанные, в первую очередь, с релаксационными переходами в полимерах ЗУП в эксплуатационном температурном диапазоне, которые сопровождаются изменением податливости материала на несколько порядков, и, как следствие, скачкообразным изменением степени поляризации.
Еще одной причиной нештатного изменения оптических свойств может стать несовершенство технологических процессов, приводящее к отклонениям геометрических параметров конструктивных элементов от проектных значений [4, 5]. В связи с этим на некоторых технологических этапах производства происходит контроль соответствия параметров изделия проектным значениям. В рамках одного из таких испытаний волокно с натягом наматывается на алюминиевую катушку и подвергается термоциклированию, во время которого контролируются оптические характеристики. Влияние силовой намотки волокна на катушку без учета защитного покрытия и контакта с катушкой было рассмотрено в работах [6, 7]. В статье [8] выполнен анализ с учетом контактного воздействия на волокно в защитно-упрочняющем покрытии при комнатной температуре и без учета несовершенства геометрии анизотропного волокна.
ПОСТАНОВКА ЗАДАЧИ
В работе методами математического моделирования выполнено исследование влияния термосилового воздействия на напряженно-деформированное состояние в анизотропном волокне и на его оптические характеристики, при однорядной силовой намотке на алюминиевую катушку, с учетом перечисленных во введении факторов, в том числе, релаксационных процессов протекающих в полимерных защитно-упрочня-ющих покрытиях при циклическом изменении температуры по заданному закону в диапазоне от -60 до 60 °C (рис. 2) и отклонений центра светопроводящей жилы от центра волокна.
Расчетная схема контактного взаимодействия катушки и волокна приведена на рис. 3. Для учета остаточных напряжений в анизотропном волокне типа Panda сформированных после высокотемпературной вытяжки использовался подход, описанный в [9]. Таким образом, на первом этапе были получены поля остаточных деформаций, которые были использованы на втором этапе в качестве начальных условий.
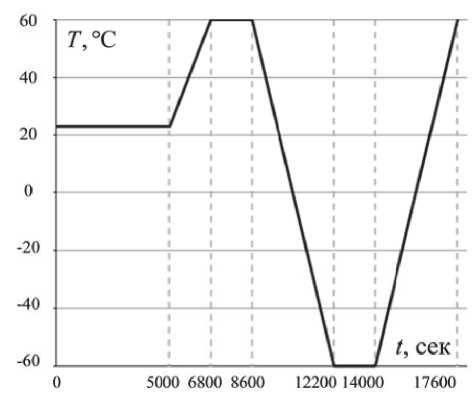
Рис. 2. Цикл изменения температуры
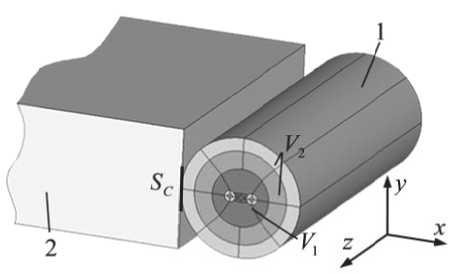
Рис. 3. Расчетная схема:
1 – оптическое волокно типа Panda, 2 – катушка, V1 – объем волокна, V2 – объем ЗУП, SC – контактная поверхность
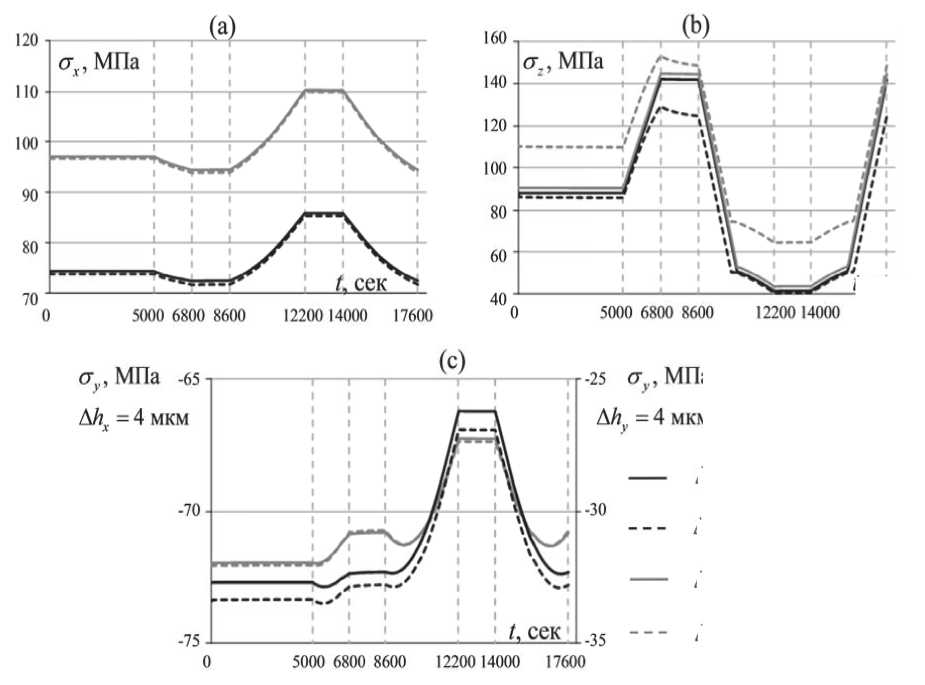
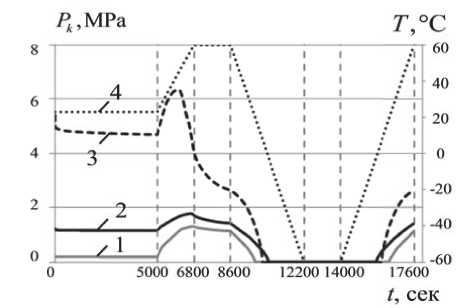
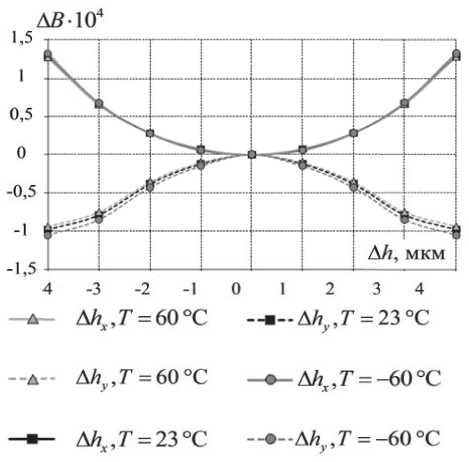
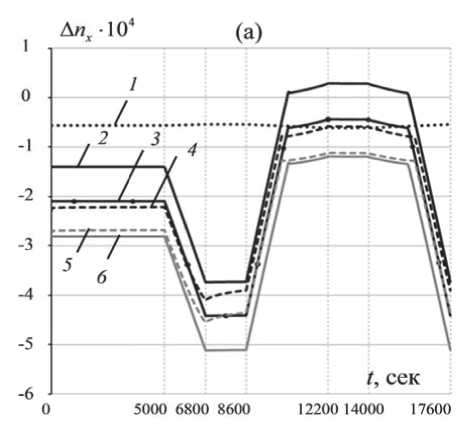
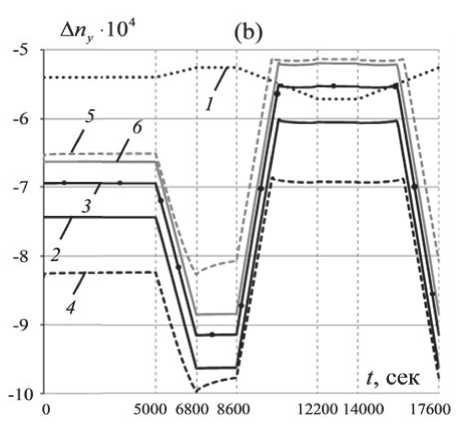
Математическая постановка описанной задачи включает в себя уравнения равновесия div где J - тензор напряжений, V - расчетный объём, X - радиус-вектор произвольной точки расчетного объёма. Геометрические соотношения с учетом малости деформаций 1 _ T 8 = 2 (Vu + (Vи) ), X е V, (2) где 8 - тензор деформаций, й - вектор перемещений. В качестве физических соотношений для конструктивных элементов волокна, состоящих из легированных кварцевых стекол, использовался обобщенный закон Гука. Учитывая, что упругие характеристики кварцевого стекла в рассматриваемом диапазоне эксплуатационных температур изменяются незначительно [10], была принята гипотеза, что они не зависят от температуры j = Х11 (8) I + 2G8 , X е V, (3) где X - параметры Ламе, G - модуль сдвиговой деформации, 11 (s) - первый инвариант тензора деформаций, I – единичный тензор. Для полимеров ЗУП использовались физические соотношения, соответствующие линейной вязкоупругой модели [11] с аппроксимацией модуля релаксации суммой экспонент <7 = KА + 2J G(t - т)d((т) -13 А(т)l), (4) где ∆ – объемная деформация, К – модуль объемного сжатия, G(t) функция сдвиговой релакса- ции: nG G(t) = Gо CG -V CG exp i=1 ^^^^^^^в t TG где G0 – мгновенный модуль, CiG – экспериментальные коэффициенты, nG – количество членов экспоненциального ряда, т° - времена релаксации. При учете влияния температуры на свойства материала используется температурновременная аналогия, при этом для вычисления приведенных времен применяется коэффициент температурно-временного сдвига, получаемый по формуле Вильямса-Ланделла-Ферри lg aT CT (T - Tb) CT + (T - Tb) , где C1T , C2T , Tb – экспериментальные коэффициенты. Граничные условия в перемещениях и напряжениях u = и, x e su, <7 • n = P, x e S7, где Su и Sст - части границы с заданными перемещениями и нагрузками соответственно, n -нормаль к поверхности. Контактное взаимодействие двух поверхностей без учета трения моделировалось соотношениями, записанными в системе координат, связанной с общей нормалью к первой поверхности в точке контакта: x01 + u1 (t) = x02 + u2 (t) - при наличии контакта, x01 + u1 (t) < x02 + u2 (t) - при отсутствии контакта, где индексы 1 и 2 относятся к соответствующим контактирующим поверхностям, x0i и ui –на-чальная координата и перемещение i-ой контактирующей точки соответственно. Численная реализация была выполнена методом конечных элементов. Предварительно по методике, изложенной в работах [9], были определены поля остаточных напряжений, формирующиеся в волокне в процессе высокотемпературной вытяжки. РЕЗУЛЬТАТЫ На первом этапе многовариантных численных экспериментов были получены поля остаточных напряжений в оптоволокне после высокотемпературной вытяжки, характерные эпюры которых приведены на рис. 4. На втором этапе были получены зависимости компонент тензора напряжений от времени, в условиях изменения температуры по приведенному на рис. 2 термоциклу. Характерные зависимости эволюции компонент тензора напряжений в центре светопроводящей жилы для двух разных отклонений геометрии волокна для катушек радиусом 50 мм и 10 мм приведены на рис. 5. Видно, что наибольшее влияние изменение температуры оказывает на стz. При нагреве катушки радиусом 50 мм до 60 °С, стz в центре светопроводящей жилы увеличивается более чем в 1,6 раза, достигая в максимуме 142-145 МПа, а при дальнейшем охлаждении до -60 °С уменьшается до 40 МПа, а изменение стx и стy не превышает 20%. На рис. 6 приведены зависимости контактного давления от температуры для двух вариантов радиуса катушки и силы натяжения волокна при намотке на катушку FT=0,2Н и FT=0,02Н. Анализ результатов позволяет сделать вывод, что при отрицательных температурах контактное давление становится равным 0. Это говорит о том, что происходит «разрыв» контакта. Характерные нелинейные участки в районе 6800-8600 секунд соответствуют релаксационным процессам в первичном защитно-упрочняющем покрытии, которое при нагреве начинает размягчаться. Для катушки радиусом 50 мм и усилия натяга FT = 0,02 Н температура соответствующая разрыву контакта равна 19 °С и -2 °С при FT = 0,2 Н, для катушки 10 мм и усилия натяга FT = 0,2 Н 7 °С. Установлено, что чем больше сила натяга и радиус катушки, тем ниже температура, при которой происходит разрыв контакта. На третьем этапе, используя известные соотношения [12, 13], связывающие компоненты тензора напряжений с оптическими характеристиками А n =- C 7 - C2 (7 - 7 ), xxyz А ny = - C7y - C2 (7x - 7z), В- = Аnx - Аny, го 2п ( C1 - C2 )J J (7x ( r, Ф)-7y ( r, Ф))|E ( r, Ф, V )|2 rdrdФ В = го 2п JJ |E (r, ф, V )| ^^ф где C1, C2 – коэффициенты фотоупругости, E – распределение интенсивности основной моды, Bi – материальное двулучепреломление, B – модовое двулучепреломление, ∆nx, ∆ny – приращение показателя преломления света, вызванное на- Рис. 4. Эпюры компонент тензора остаточных напряжений после вытяжки, вдоль линии, соединяющей центры силовых стержней: (а) - Ahx = 4 мкм; (b) - Ahy = 4 мкм L сек Айх =4 мкм, /?ы= 10 мм ДАГ = 4 мкм, /?ы= 50 мм ДЛг =4мкм, /?ка1 = 10 мм ДЛ. = 4 мкм, /?ка1 = 50 мм Рис. 5. Эволюция компонент тензора напряжений в центре светопроводящей жилы (FT = 0,2 Н): (a) - сх,(b) - aZ,(c) - аy Рис. 6. Эволюция контактного давления: 1 – FT = 0,02 Н, Rkat=50 мм, 2 – FT = 0,2 Н, Rkat=50 мм, 3 – FT = 0,2 Н, Rkat=10 мм, 4 – график с изменением температуры пряженно-деформированным состоянием, были получены зависимости показателя преломления и модового двулучепреломления от отклонений геометрии волокна и температуры (рис.7, 8). На рис.7 приведена зависимость ∆B=B’-B0 от ∆hx и ∆hy при разных значениях температуры, где B’, B0 – двулучепреломление волокна с отклонением гео -метрических параметров и с проектной формой соответственно. В результате анализа полученных данных установлено, что отклонение светопро -водящей жилы по оси OY более чувствительно к изменению температуры, о чем свидетельствует больший разброс кривых на рис. 7, который растет с увеличением отклонения ∆hy, из чего также можно сделать вывод, что чем больше отклонение геометрии волокна, тем большее влияние на его оптические характеристики оказывает измене -ние температуры. Нелинейное изменение откло -нений показателя преломления света на участке Рис. 7. Зависимость отклонения двулучепреломления от ∆h – смещения светопроводящей жилы волокна при Rkat=50 мм выдержки после нагрева с 6800 по 8600 секунды (рис. 8) коррелирует с эволюцией контактного давления (рис. 6) и становится более выраженным при уменьшении радиуса катушки. Этот эффект объясняется тем, что при нагреве податливость внешнего полимерного покрытия, находящегося в состоянии релаксационного перехода, увеличивается более чем на порядок и под действием кон -тактного давления в условиях выдержки при тем -пературе 60 °С, в нем развиваются деформации ползучести, за счет чего происходит частичная разгрузка растянутого кварцевого волокна. При больших радиусах намотки, этот эффект практически незаметен, т.к. контактное давление существенно меньше (рис. 6). Рис. 8. Эволюция отклонения показателя преломления в условиях термоцикла (а) по оси x, (b) по оси y: 1 – свободное волокно без отклонений геометрии; 2 – ∆hx = 4мкм, Rkat=50 мм; 3 – волокно без отклонений геометрии, Rkat=50 мм; 4 – ∆hx = 4мкм, Rkat=10 мм; 5 – ∆hy = 4мкм, Rkat=10 мм; 6 – ∆hy = 4мкм, Rkat=50 мм ЗАКЛЮЧЕНИЕ В рамках исследования построена численная модель контактного взаимодействия катушки с анизотропным оптическим волокном в защитно-упрочняющем покрытии при силовой однорядной намотке в условиях термоцикла. В результате проведенных многовариантных численных экспериментов были получены зависимости, описывающие эволюцию полей напряжений в волокне, а также связанные с ними оптические характеристики. Анализ полученных данных позволяет сделать следующие выводы: 1. Изменение температуры в рассматриваемом диапазоне оказывает существенное влияние на НДС волокна. 2. При охлаждении происходит отрыв волокна от алюминиевой катушки. Температура, при которой это происходит, зависит от радиуса катушки и усилия натяга, с которым наматывалось волокно. 3. За счет деформаций ползучести во внешнем защитно-упрочняющем покрытии, развивающихся под действием высокой температуры и контактного воздействия, происходит частичная разгрузка кварцевого волокна.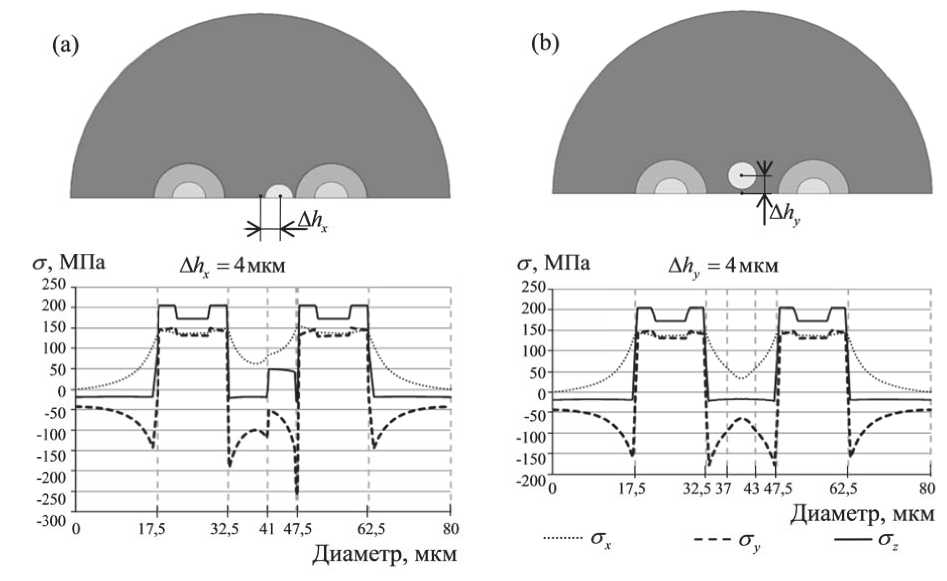
Список литературы Исследование оптико-механических характеристик волокна в условиях термоцикла
- Lee B. Review of the present status of optical fiber sensors // Opt. Fiber Technol. 2003. Vol. 9. P. 57-79.
- Transverse load sensor based on Mach-Zehnder interferometer constructed by a bowknot type taper/ W. Lou, F. Shentu, Y. Wang, C. Shen, X. Dong // Opt. Fiber Technol. 2018. Vol. 40. P. 52-55.
- Fiber-optic bend sensor using LP21 mode operation/ Y. Fan, G. Wu, W. Wei, Y. Yuan, F. Lin, X. Wu // Opt. Exp. 2012. Vol. 20. P. 26127-26134.
- Семенов Н.В., Труфанов Н.А., Адамов А.А. О технологических несовершенствах геометрических параметров силового стержня для заготовки оптического волокна Panda // Научно-технический вестник информационных технологий, механики и оптики. 2014. №1(89). С.54-59.
- Численно-экспериментальное исследование влияния технологических несовершенств геометрии силовых стержней на напряженное состояние и оптические характеристики световода типа «Панда» / Е.В. Праведникова, Н.В. Семенов, А.Н. Труфанов, Н.А. Труфанов // Известия Самарского научного центра РАН. 2014. Т. 16. № 6. С. 89-94.


