Исследование основ нестационарного тепло- и массообмена в вентилируемой воздухом массе плодоовощной продукции

В современной практике хранения загрузка плодоовощной продукции в хранилищах осуществляется в виде штабелей, сформированных из контейнеров с продукцией. Для рационального использования подаваемого воздуха и максимального использования грузового объема хранилищ контейнеры размещаются в соответствии с технологическими схемами: плотная загрузка; П-образное складирование; складирование с технологическим колодцем; П-образное встречное складирование и т.д.. В процессе хранения в плодоовощной продукции продолжаются жизнедеятельные процессы, сопровождающиеся выделением теплоты и влаги, что приводит к самосогреванию штабеля. В объеме его устанавливаются температурно-влажностные поля, градиенты которых зависят от системы воздухораспределения, формы, размеров и плотности штабеля, вида продукции, а также от способов и интенсивности вентилирования хранилища. Эффективный отвод теплоты из штабеля и связанное с ним выравнивание полей температур в его объеме будут происходить только тогда, когда аэродинамическое сопротивление штабеля будет меньше давления, создаваемого разностью плотностей воздуха в хранилище и штабеле, либо давления, развиваемого вентиляторами.

При рассмотрении хранения плодоовощной продукции (ПП) в штабеле выделяют два режима теплообмена:

• -    стационарный теплообмен с окружающей воздушной средой в период основного хранения, когда происходит только выделение теплоты дыхания и влаги, и процессы ассимиляции их принимаются стационарными во времени, интенсивность которых зависит от изменения температуры хранения;

• -    нестационарный теплообмен, в процессе которого понижается температура продукции и уменьшается количество выделяемой физиологической теплоты. Этот режим теплообмена протекает в хранилищах начиная с осушки влажной поверхности, т.е. сразу после загрузки и до начала периода хранения. Процесс тепломассообмена насыпного слоя продукции с вентилирующим воздухом характеризуется сложностью, многофакторностью явлений теплообмена, массообмена и аэродинамики воздушного потока.

Наиболее точно процессы тепломассопереноса воспроизводятся на основе системы дифференциальных уравнений Рейнольдса:

• -    уравнение движения (Навье-Стокса):

  э^

  ^{д и} ф  1 ^д V U ф J

  дт ⁺ 2    д х

  
  

  1 д Р

  Р е д х

  
  

  + Ф х +

  
  
  
  

  д х "

  
  

  V

  
  

  U ² Ф

  
  

  - уравнение неразрывности:

  
  

  дт

  - уравнение баланса тепловой энергии:

  
  

  ^др %₀ + ^д ( p U™

  
  

  д >

  
  

  = 0;

  
  

  1 д д 1

  U , дт д х ф

  
  

  ^a tFy 1

  
  

  ^tпов U_™п

  
  

  —

  
  

  te )

  
  
  
  

  - уравнение баланса массы вещества в потенциалах влажности или влагосодержания:

•« я _    ^aeF_ya _to __fl х

Uф дт д х ( Св Р е VфП      ® ^е )

¹ * + a d = a d—, ( -

U™ ^{дт д} U™ п р ^  ^ ^

Главная сложность использования этой системы уравнений связана с отсутствием надежных методов численного решения ее на ПЭВМ.

Теоретические и экспериментальные исследования И.Л. Волкинда, Г.М. Позина [1], В.З. Жадана [2] и других показывают, что в насыпи плодоовощной продукции значительных размеров при неработающих и работающих системах активной вентиляции (САВ) в теплообмене с контактирующим воздухом участвует лишь верхний слой насыпи толщиной 0,3....0,4 м, что с некоторыми допущениями справедливо для беззакромного хранения (рис.1).

При хранении в контейнерах необходимо учитывать, что продукция размещается в хранилище в виде штабелей, омываемых воздухом, практически, со всех сторон. В штабеле плодоовощной продукции всегда наблюдается движение воздуха с меньшей или большей интенсивностью. Выражение для определения коэффициента теплопроводности штабеля Х _шт = е Х _в +(1- е )= Х _пр [3] справедливо для условия неподвижного воздуха внутри штабеля, что в практике хранения плодов и овощей отсутствует. В действительности на величину коэффициента Х шт , помимо молекулярной теплопроводности воздуха и продукта, значительное влияние оказывает конвективный и лучистый теплообмен.

Выполненный анализ применяемой технологии хранения ПП в хранилищах с активным вентилированием позволяет выделить основные требования к теоретической модели тепло- и массообмена в насыпном слое. Модель должна:

• -    иметь форму краевой задачи с заданными граничными условиями;

• -    описывать процессы теплообмена, массопереноса, движения воздушных масс в массе ПП - с учетом их взаимосвязей;

• -    быть нестационарной и иметь уравнения в дифференциальной форме;

• -    быть общей как для расчета теплообмена при активном вентилировании в период охлаждения, так и для основного периода хранения продукции в режиме естественной вентиляции.

В общем случае тепло- и массообмен между массой продукции и воздуха, находящихся в насыпи, можно выразить системой дифференциальных уравнений вида [4]:

^д =----- a v ----г ( T - т ) +----- qv ----г •

^{д р} с^Сн ^{( 1 £} ск )          ^р с^Сн ^{( 1 £} ск )

дТ + £ск дТ =  av дх  V дh  р С V

н

Решение системы (6...7), которой соответствует расчетная схема, представленная на рисунке, ищут при начальных и граничных условиях обычно одного рода [5]. Вместе с тем, как справедливо будет сказать, различий в решении этой системы уравнений много.

В работах [6,7] применено аналитическое решение задачи охлаждения насыпи, полученное при помощи преобразования Лапласа. Другие исследования использовали решения, полученные А. Анце-лиусом и Т. Шуманом. Для решения системы уравнений (6...7) В.И. Бодровым использован также системный метод.

Различия в ее решении заключаются в следующем:

• -    принимаются при различных допущениях значения величин биологических тепловыделений:

qv= 0 - [3,8,9] и др.,(8)

qv = qoexp(bt) - [9] ,(9)

qv = const - [6],(10)

• -    допускаются различные начальные условия:

t = T = Tн   τ=0 - [8] и др.,(11)

T -t t = T = Tн - н o x    τt=0 - [10].(12)

h

Авторами работы [9] получено аналитическое решение для более сложного случая, чем описываемое системой (6...7), с учетом реальной теплопроводности массы продукции. При этом уравнение (6) заменено уравнением теплопроводности для контейнерной тары с внутренним источником теплоты.

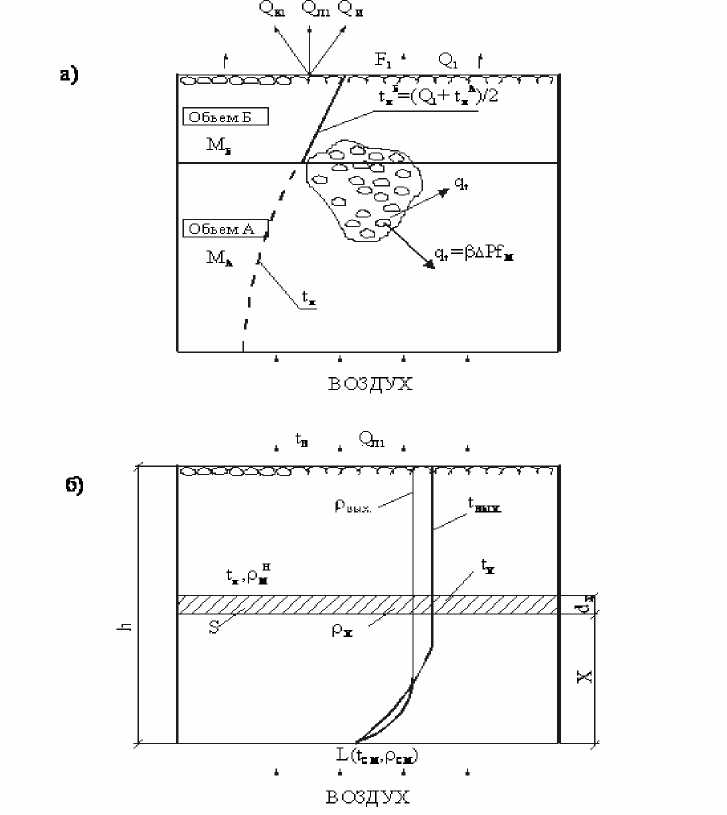
Рис. Расчетные схемы тепло-и массообмена в насыпном слое плодоовощной продукции при неработающей активной вентиляции (а) и в период работы активной вентиляции (б)

Знание характера распределения температурно-влажностных полей в объеме контейнерного штабеля, в зависимости от системы вентилирования, позволяет определить оптимальные размеры штабеля, в котором будут поддерживаться температурно-влажностные условия, способствующие наиболее качественному и длительному хранению, при имеющемся инженерном оборудовании, продукции.

Другой подход к расчету распределения температуры в штабеле представил J.G.Tohumak [11], который рассмотрел штабель как неограниченную пластину, составленную из крупнозернистых элементов. Вместо коэффициента молекулярной теплопроводности твердого тела им введено значение эквивалентного коэффициента теплопроводности ( Х _экв).

Для установления температурных распределений в штабеле с внутренними источниками теплоты мощностью Q шт использована методика решения обобщенной задачи по охлаждению неограниченной пластины толщиной 2R при граничных условиях третьего рода. Решение в безразмерных величинах для вентилируемого штабеля представлено в виде:

_е = Т ( % , т ) - To Тв — То

г

= 1 + 0,5 Ро 1 -

I

х ²    2

R ^{2 +} Bi ,

го 2 1 - n =11

Po

2 ^ n

x

An cos Ц п — exp

(- Ц 2 nFo )

На наш взгляд, полученные результаты носят теоретический характер, т.к. они выполнены для тел простой формы (куб, пластина), а на практике штабель с продукцией имеет форму параллелепипеда с самым разным соотношением линейных размеров.

В случае равномерного распределения вентиляционного воздуха, подаваемого по схеме «снизу вверх» по площади штабеля, в последнем будут иметь место градиенты температуры и влагосодержания только по высоте штабеля. В основной период хранения изменение температуры воздуха по высоте штабеля происходит нелинейно, т.к. теплота дыхания отводится явным и скрытым путями. Ввиду того что температурно-влажностное состояние воздуха по высоте штабеля меняется, различно и соотношение между скрытым и явным отводом теплоты от продукции. По этой же причине интенсивность влаго-выделений по высоте штабеля также неодинакова, что приводит к нелинейному изменению влагосодер- жания воздуха по высоте.

Г.М. Позиным в работе [6,7] установлено, что температура вентиляционного воздуха при прохождении через насыпь продукции изменяется по высоте. Для нахождения закона ее изменения выделен в насыпи по высоте Х элементарный слой dх, при прохождении через который температура воздуха изменяется на dt (рис. 1б). Для слоя dх приведено дифференциальное уравнение сохранения энергии в виде:

М L_C M (1/S)C e dx = a F M F m (1/S h_Hac)(t M - t x ) dx.                               (14)

Аналогично приведенным выше рассуждениям записано дифференциальное уравнение изменения парциального давления водяных паров в воздухе:

М L cM (1/S)bdP x= = P f M F m (1/S hXP M^ P x ) dx.                            (15)

После интегрирования уравнения (14) и (15), получено безразмерное значение по высоте насыпи: - температуры:

9 = t%  tм = ex_p - ₀,ю4 ⁽¹ 2с ) *

tсм ^- tм [            е Ск d

- парциального давления водяных паров:

Р =

Рх

н Рм

Рсм

н Рм

= exp

- 0,140

^{(1   е} ск ) ^

^ь ск d

С помощью полученных зависимостей (14...17) авторами этой работы сделаны следующие выводы:

• -    изменение температуры и влагосодержания воздуха при его прохождении через слой продукции зависит только от скважности насыпи и диаметра составляющих ее элементов; температура воздуха нарастает достаточно быстро и уже на высоте 0,3...1 м становится практически равной температуре массы ПП; воздух насыщается влагой еще быстрее (для картофеля практически полное насыщение имеет место при высоте слоя порядка 0,6 м).

Из анализа выводов следует: температуру воздуха при выходе из насыпи в верхнюю зону можно считать равной температуре насыпи (tB ® tнаc); относительная влажность воздуха при выходе в верхнюю зону близка к равновесной ~ 100%; при активном вентилировании происходит постепенное удаление тепло- и влагоизбытков из насыпи продукции: сначала из нижних слоев, а затем фронт понижения тем- пературы воздуха и уменьшения влагосодержания перемещается вверх (при подаче воздуха по схеме «снизу-вверх»).

Анализ динамики температурно-влажностных полей в насыпи продукции, находящейся в контейнере, позволяет выявить пути снижения потерь продукции и предотвратить создание условий, способствующих образованию конденсата на поверхности сырья.

Основные условные обозначения d – диаметр, м; влагосодержание воздуха, г/кг; К – коэффициент теплопередачи, Вт/(м2 К); a - коэффициент температуропроводности, м2/с; b – градиент температур по высоте штабеля и насыпи продукции, 0С/м; Ср – удельная массовая теплоемкость, кДж/(кг 0С); T, θ - температура, 0С; tв ,tм – температура внутреннего воздуха, температура массы продукции 0С; H, hнас –высота помещения, высота насыпи продукции, м; М – масса продукции, кг; qv – удельный тепловой поток, Вт/м2; qt – удельная теплота дыхания продукции, Вт/т; Вт/м3; г/(м3 ч); at, aв – коэффициент теплоотдачи, Вт/(м2 К); λ - коэффициент теплопроводности, Вт/(м К); d – диаметр, м; β - коэффициент мас-сообмена, кг /(м2Па сек); F – площадь поверхности продукции м2; L, Lm, Lv – удельные объемные расходы воздуха м3/(м2 ч); м3/(т.ч); м3/(м3 ч); ΔРо – аэродинамическое сопротивление, Па; Р – парциальное давление водяного пара, Па; ΔР – потери давления, Па; Rо – сопротивление теплопередаче ограждения, (м2 0С)/Вт; ρ - плотность воздуха, кг/м3; µ - коэффициент динамической вязкости, м2/с; V – объем, м3; υ- скорость, м/с; S - площадь поверхности штабеля, насыпи, м2/м3, м2/т; aθ, ad – коэффициенты массообмена, г/(м2 ч Па); εск – порозность насыпного слоя (скважность); G – массовый расход воздуха, кг/ч; τ - время, ч; температура внутренней поверхности, 0С; ϕ - относительная влажность воздуха, доли %; x, y, z – текущие координаты.