Исследование особенностей движения астероидов главного пояса

Рассматривается финансовая система, состоящая из 13-ти региональных банков Ростовской области, действующая в периоде 2009 – 2017 г.г. по материалам публичного архива [1] приложения работы [2]. В соответсвующем периоде наблюдения материалы представлены в таблицах (пример, 2014 г., табл. 1). Работа выполняется в среде MATLAB R2014a M-BOOK with word. В представленных материалах факторы описания зависимы: в активы включены кредиты, а в депозиты – вклады населения.

Для анализа при независимых ортогональных факторах введём новые факторы "Капитал банка", "Кредиты", " Др. активы", "Вклады населения", "Др. депозиты" и проведём расчёты рабочего трёхмерного массива F (13, 13, 5) по алгоритму 1

БАНКИ ПО СОСТОЯНИЮ НА 01.01.2014 (тыс. руб.)

п/п Банки Капитал Активы Кредиты Депозиты Вклады населения 1 Дон-Тексбанк 312908 1580631 656586 624604 624604 2 Донкомбанк 523332 6917497 4449734 2770783 2143925 3 Донхлеббанк 273473 2810992 1249875 1202233 1073233 4 Земкомбанк 586530 3430334 1068692 624587 563587 5 Капиталбанк 320524 2142763 739876 999418 821351 6 Кредэксбанк 494167 3228777 1602296 1120678 760979 7 РостФинанс 301926 3164207 825177 1054206 191247 8 Российский нац. банк 481216 3568235 2095508 1739407 151528 9 Сельмашбанк 277564 1456775 785702 403491 214041 10 Стелла-Банк 269700 3367684 1281881 960190 762590 11 Таганрогбанк 235616 574819 234642 137561 87561 12 Центр-инвест 9586325 112061472 65041445 46753465 37389622 13 Южный Региональный Банк 271420 569443 365156 62443 62443 foBrn0(=:,:1,n:s)i=ze[(AA,(:3,1),n) A(:,3,n) A(:,2,n)-A(:,3,n) A(:,5,n) A(:,4,n)-A(:,5,n)];

B = cat(1, B0, sum(B0)/size(B0,1));

for k = 1:size(B,1)

X(k,:,n) = B(k,:,n)./B(size(B,1),:,n);

end end

%% Находим:

% единичный эталон e = X(size(X,1), :,n);

% вектор весовых коэффициентов p= e/sum(e);

% и метрический тензор

P = diag(p);

for n = 1:size(A,3)

for k = 1:size(A,1)

for l = 1:size(A,1)

cov2(k,l,n) =((X(k,:,n)*P*X(l,:,n)')/sqrt((X(k,:,n)*P*X(k,:,n)')* (X(l,:,n)*P*X(l,:,n)')))^2;

F(k,l,n) = sqrt(atan((1 - cov2(k,l,n))/cov2(k,l,n)));

end end end

Алгоритм 1. Расчёт основных рабочих массивов.

Каждый элемент F (:, :, 1:5) массива представлен квадратной симметрической матрицей размерности 13x13 оценки вращательной симметрии в бинарном соответствии ( x, у ) банков соответствующего периода наблюдения, что отвечает оценке структурных расхождений данных объектов в соответствующий момент наблюдения. Оценка состояния системы проводится по равноотстоящим на временном горизонте срезам. В каждый фиксированный момент времени метрическимй тензор P является исчерпывающей характеристикой для состояния любого объекта как случайной величины в оценке его динамики, а его предыдущее состояние в оценке играет роль памяти. Т.о., рассматриваемый процесс эволюции системы относится к типу немарковских процессов с последействием, т.е., в частности, к проблемам квантовой механики и использования её терминологии в описании.

Покажем, что массив F действительно является оценкой структурных сдвигов, т.е. оценкой динамики качества объектов и качества системы как целого и, как следствие, может служить оценкой эволюции кластеров при её факторизации.

Действительно, если записать объект в полярной системе координат, полярная ось которой фиксирована элементом y, x = r (x) е1ф (x y ), то для бинарного соответствия (х, у) любых объектов x множества X (см. Алг. 1), как линеала, будет справедливо основное метрическое тождество [3]

D(x, у) = /л2(x, у) + Г(x, у), которое при фиксировании направления у ЕX единичным вектором е =е(у), принимает вид r2(x) = E2(x) + V(x),  E (x) = e'Px.

В двумерном ортогональном представленнии элемента x комплексным числом x = E (x) + iV1/2(x)

находим на любом бинарном соотвествии ( x, y) e X x X значение его аргумента и представление на всём временном горизонте функции качества

F ( x, y, t ) = {ф( x, y, t ) = arctg ( V ^%( x ( 1 1 ), 1 2 )/ E ( x ( 1 1 ), 1 2 )): ( x ( 1 1 ) , y ( 1 2 )) e X x X x T,

12 = 11 = t}, которая описывает состояние объекта и представляет диалектическое единство сходства и различия объектов по качественным признакам. Чем больше на бинарном соответствии элементов значение данной функции, тем больше между ними структурное различие. Поэтому она может служить инструментом таксономии множества объектов по качественным признакам.

Задаваясь определённым порогом содержания в объекте того или иного свойства, можно выделить его из общего множества и проследить качественное изменение его во времени. Принимая данную функцию за дистанционную, отметим, что она возрастает при увеличении качественного различия между её аргументами x и y , т.е. между двумя различными состояниями, а при качественном подобии x = Ay +a обращается в нуль.

Рассмотрим классификацию системы банков в наблюдаемый момент t = 1, что отвечает периоду её состояния на 01.01.2009 года. При этом будем отмечать соответствующий банк его порядковым номером в списке, см. таб. 1.

Качественному состоянию системы в периоде наблюдения t = 1 отвечает дистанционная функция F (:, :, 1). Избавляясь от единичной размерности и вводя для неё новое обозначение, приходим к табл. 2.

F1 = squeeze(F(:,:,1))

F1 =

0  0.1333  0.0720  0.9582  0.9801 0.9891					0.9849	0.4243	0.9572	0.5813	0.4504	0.6578	0.7454
0.1333	0  0.0729		0.8622	0.9059	0.9207	0.3052	0.8920	0.5131	0.3149	0.5663	0.6697
0.9083
0.0720	0.0729	0	0.8971	0.9436	0.9480	0.3561	0.9092	0.5151	0.3735	0.6073	0.6731
0.9484
0.9582	0.8622	0.8971	0	0.4221	0.3298	0.5642	0.1873	0.4618	0.6732	0.3892	0.5837
0.3601
0.9801	0.9059	0.9436	0.4221	0	0.2071	0.6963	0.4051	0.7508	0.8576	0.2987	0.9712
0.0751
0.9849	0.9207	0.9480	0.3298	0.2071	0	0.6667	0.2597	0.6871	0.8468	0.3184	0.8967
0.1726
0.4243	0.3052	0.3561	0.5642	0.6963	0.6667	0	0.6389	0.4048	0.1761	0.3686	0.5426
0.6666
0.9572	0.8920	0.9092	0.1873	0.4051	0.2597	0.6389	0	0.4753	0.7877	0.3905	0.6517
0.3660
0.5813	0.5131	0.5151	0.4618	0.7508	0.6871	0.4048	0.4753	0	0.4528	0.4812	0.2554
0.7285
0.4504	0.3149	0.3735	0.6732	0.8576	0.8468	0.1761	0.7877	0.4528	0	0.5407	0.5007
0.8252
0.6578	0.5663	0.6073	0.3892	0.2987	0.3184	0.3686	0.3905	0.4812	0.5407     0		0.7386
0.2961
0.7454	0.6697	0.6731	0.5837	0.9712	0.8967	0.5426	0.6517	0.2554	0.5007  0.7386    0
0.9363
0.9891	0.9083	0.9484	0.3601	0.0751	0.1726	0.6666	0.3660	0.7285	0.8252  0.2961  0.9363

Видим, что объекты 1, 2 и 3 могут составлять определённый кластер, от которого объекты 4, 5, 6, 8 и 13 находятся на значительном качественном расстоянии. Заданием порога близости L объектов на бинарном множестве {0, 1} данная матрица обращается в разреженную матрицу S1 из нулей и единиц, где единица отвечает близости объектов на данном пороге, а нуль -их расхождению.

Применением метода Далмейджа-Мендельсона построим вектор сходства g1 такой, что матрица R1 имеет полный столбцовый ранг. Последние строки алгоритма формируют графики разреженной матрицы и матрицы после упорядочения, рис .1.

L = 0.35;

for k = 1:13

for l = 2:13;

if F1(k, l) < L

S1(k, l) = 1;

S1(l, k) = 1;

else

S1(k, l) = 0;

S1(l, k) = 0;

end end

S1(k,k) = 1;

end g1 = symrcm(S1)

R1 = S1(g1,g1);

subplot(1,2,1),spy(S1);

subplot(1,2,2), spy(R1)

Алгоритм 2. Группировка объектов по качественному сходству.

Вектор максимального качественного сходства имеет вид g1 = [3 1 2 10 7 8 4 6 13 11 5 12 9]

Рисунок упорядоченной матрицы показывает, что система состоит из трёх кластеров Class1 = Set1 ∪ Set2, Class2 = Set3 ∪ Set4 и Class3 = Set5, содержащих множества Set1 = (3, 1, 2), Set2 = (2, 10, 7), Set3 = (8,4,6), Set4 = (6, 13, 11, 5), Set5 = (12, 9). При этом Set1∩Set2 = 2 и Set3∩Set4 = 6.

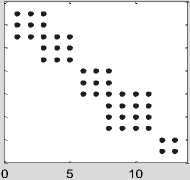
nz = 45

Рис.1. Графическая интерпретация разреженной матрицы и матрицы после MD-декомпозиции.

Каждая матрица X(:, :, t), t = 1:8, массива X (алг. 1) определяет координаты объектов в декартовом пространстве с единичным масштабным кубом [0, 1]5, в котором диагональ куба выполняет роль эталона e. Поскольку пространства l1 и l2 связаны выпуклым преобразованием, то, исходя из массива X, анализ проведём в пространстве последовательностей, суммируемых с первой степенью, т.е. в l1. В этом пространстве качество объекта определено в пропорциях его координат и лучше просматривается в отнесении их к максимальному значению координаты, а количественной объёмной характеристикой может служить индикатор нормы вектора-строки матрицы X1 как среднего её элементов (алг. 3). Более того, можно обратиться к экономическому содержанию показателей.

%% Устанавливаем число объектов анализа n = 1:13;

% Из массива A фиксируем матричное описание в надлежащем периоде наблюдения и удаляем

% единичную размерность

X1 = squeeze(X(:,:,1));

% Находим для каждого объекта максимальное значение фактора для более наглядного

% представаления качества в пропорциональных отношениях их числовых характеристик X1maxStr = (max(X1'))';

% Для каждого объекта вычисляем объёмную характеристику

Modul1 = (sum(X1')/5)';

%% Вычисляем пропорциональные отношения факторов for k = 1 : 14

X1str (k, : ) = X1(k,: )/X1maxStr(k,1);

end

% и составляет таблицу в исходном списочном порядке объектов пропорциональных отношений факторов

% и модульной оценке объектов в процентном выражении

X1strmod = cat(2, n', X1str(1:13,1:5), 100*Modul1(1:13,1)/sum(Modul1(1:13,1)))

%% Формируем характеристики классов

Class1=cat(1, X1strmod(3,:), X1strmod(1,:), X1strmod(2,:), X1strmod(10,:), X1strmod(7,:)) SUM1 = cat(2, sum(Class1(:,2:6)/5),sum(Class1(:,7)))

Class2=cat(1,        X1strmod(8,:), X1strmod(4,:), X1strmod(6,:), X1strmod(13,:),

X1strmod(11,:),X1strmod(5,:))

SUM2 = cat(2, sum(Class2(:,2:6)/6),sum(Class2(:,7)))

Class3=cat(1, X1strmod(12,:), X1strmod(9,:))

SUM3 = cat(2, sum(Class3(:,2:6)/2),sum(Class3(:,7)))

Алгоритм 3. Вычисление качества в отношении координат и объёмной характеристики объектов с классовым расслоением.

Из табл. 3 видим, что данная система имеет расслоение на три класса. Объекты первого и второго классов сравнительно небольшие и занимают в финансовой сфере деятельности свою нишу. Деятельность первой группы банков сосредоточена в активах и обеспечивает обслуживание вкладов населения. Банки второй группы, как-бы, являются хранилищем капиталов. Обе группы совсем не интересны для депозитариев. Деятельность банков третьей группы равномерно распределена по всем факторам, а банк Центр-инвест (№ 12) наиболее привлекателен для депозитов, вероятно, как крупнейший банк региональной системы (обеспечивает 83% деятельности системы в целом), который они вероятно считают наиболее надёжным.

В процессе функционирования системы объекты могут переходить из класса в класс и образовывать новые классы. В данном примере могут быть до тридцати

Таблица 3.

Оценки объектов и их качественная классификация (на 01.01.2009 год).

Классификация банков W Качественное отношение факторов Объёмный индекс (%%) 1 2 3 4 5 3. 0.4860 0.5469 0.3592 1.0000 0.0610 2.2269 1. 0.4375 0.5426 0.2813 1.0000 0.0216 1.0287 СЛ СЛ й и 2. 0.5344 0.5175 0.4352 1.0000 0.0313 1.6719 10. 0.7446 0.6769 0.9812 1.0000 0.1422 2.6090 7. 0.9998 0.8459 0.8571 1.0000 0.0728 0.3053 Сред нее 0.6405 0.6260 0.5828 1.0000 0.0658 7.8419 8. 1.0000 0.5369 0.2773 0.2071 0.3575 1.3067 о о kJ 4. 1.0000 0.4604 0.5002 0.2169 0.3530 3.0582 6. 1.0000 0.4448 0.2191 0.1590 0.0610 1.2526 СЛ й и 13. 1.0000 0.2711 0.2747 0.2038 0.0156 0.8531 11. 1.0000 0.4507 0.3409 0.5315 0.0405 0.3401 5. 1.0000 0.2368 0.2096 0.2382 0 0.2509 Сред нее 1.0000 0.4001 0.3036 0.2594 0.1379 7.0616 СЛ й и 12. 0.7825 0.8835 0.9089 0.8535 1.0000 83.2020 9. 1.0000 0.7781 0.5768 0.9076 0.7097 1.8945 Сред нее 0.8913 0.8308 0.7428 0.8805 0.8548 85.0964 различных кластеров. Так, к 2017 году система становится плотнее и на пороге расслоения L = 0.35 1-й, 7-й, 8-й, 11-й и 13-й банки попадают в отдельные кластеры. Остальные банки образуют попарно зависимую цепь. И лишь с порога L = 0.32 происходит расслоение, представленное в табл. 4.

Сопоставление данных таблиц говорит о том, что под воздействием изменений окружающей данную систему среды и внутренней финансовой среды системы объекты меняют ориентацию и мощность. Происходит постоянная динамическая перестройка (деформация) системы. Её объекты постоянно меняются количественно и качественно.

Таблица 4

Оценки объектов и их качественная классификация (на 01.01.2017 год).

Классифик ация банков		и ей И	Дифференциальные характеристики качества					Интегра льный индекс (%%)
			1	2	3	4	5
	I	1	1.0000	0.3041	0.3409	0.4801	0	0.7785
		12.	0.8092	0.9942	0.7834	1.0000	0.9353	71.2686
		2.	0.7480	0.8900	0.5805	1.0000	0.3978	3.2179
	п	3.	0.5307	0.5310	0.6006	1.0000	0.2196	2.0956
		Сре днее	0.6959	0.8051	0.6548	1.0000	0.5176	76.5821
		10.	0.8835	0.4164	1.0000	0.5287	0.1773	1.3663
	ш	4.	0.7371	0.2854	1.0000	0.2645	0.0142	2.2179
о о й R		Сре днее	0.8103	0.3509	1.0000	0.3966	0.0958	3.5841
		9.	1.0000	0.5826	0.6603	0.3170	0.3503	1.1379
		6.	1.0000	0.5182	0.5535	0.4066	0.4604	2.2869
	№	5.	1.0000	0.5627	0.7081	0.5648	0.9070	4.5882
		Сре днее	1.0000	0.5545	0.6406	0.4295	0.5726	8.0130
	V	7.	0.2421	0.1543	1.0000	0.2707	0.0927	4.0272
	№	8.	0.3317	0.2686	0.3792	0.0567	1.0000	5.5708
	W	11	1.0000	0.1766	0.1241	0.0576	0.2687	0.5841
	ш	13	1.0000	0.2091	0.4576	0.0466	0	0.8602

В данной работе автор не ставит перед собой цель раскрытия деятельности некоей региональной финансовой системы под действием изменения внешних и внутренних условий (о некоторых динамических аспектах данной системы банков можно посмотреть на сайте [4]), а лишь желает на конкретном числовом примере показать элементы анализа эволюции некоторой системы как материалистического объекта в философском содержании понятия [5], исходя из фундаментальности основного метрического тождества.