Исследование особенностей фокусировки вихревых супергауссовых пучков при изменении высоты дифракционного аксикона

Дифракционный аксикон (кольцевая решетка) аналогично действию конического аксикона формирует протяженный световой отрезок вдоль оптической оси [1, 2]. Увеличивать размер фокального отрезка можно изменением радиуса освещающего луча или дополнением оптической системы регулируемой линзой или аксиконом, получая динамический фокус [3, 4]. Хорошо известно применение аксикона для ряда приложений, среди которых можно отметить тестирование материалов и устройств [5], метрологию [6], оптическое микроманипулирование [7–9].

Уменьшение размера изготавливаемых аксиконов (вплоть до микро- и наноуровня) расширяет область их применения [10– 15] и дает возможность использовать их в том числе для формирования световых полей с заданной структурой амплитуды, фазы и поляризации. Малые размеры оптических элементов также означают необходимость применения строгой электромагнитной теории для проведения моделирования [16]. Если период кольцевой решетки будет меньше длины волны, то субволновый аксикон является метаповерхностью, благодаря которой можно получить преобразование линейно-поляризованного лазерного излучения в цилиндрически-поляри-зованное излучение [17]. Если числовая апертура становится больше предельной, то энергия входного пучка перераспределяется в затухающие волны [18].

Дальнейшее уменьшение периода приводит к качественно другим эффектам [10, 19].

Гауссовы пучки и оптические вихри часто используются для решения ряда задач в оптике [20], в том числе передачи информации по оптоволокну [21], в квантовой информатике [22], в системах беспроводной связи [23]. Также ранее было продемонстрировано применение цилиндрических векторных пучков для решения задач резкой фокусировки и поляризационно-амплитудной модуляции фокальных распределений [24, 25]. Также было продемонстрировано, что состояние поляризации оказывает наибольшее влияние на продольную составляющую электрического поля [20, 26].

В данной работе исследуется влияние изменения высоты высокоапертурного дифракционного аксико-на на фокусировку мод Лагерра–супергаусса (1,0), а также супергауссовых пучков с радиальной и круговой поляризацией. Ранее было показано влияние изменения толщины подложки на картину дифракции ограниченной плоской волны на дифракционных ак-сиконах с различной числовой апертурой, где толщина менялась от 0,2λ до 0,3λ [20]. В данной работе меняется высота рельефа дифракционного аксикона в пределах от 0,25λ до 3λ. Моделирование осуществлялось методом конечных разностей во временной области (FDTD), реализованном в свободно распространяемом программном продукте Meep.

1.    Прохождение супергауссовых пучков через бинарный дифракционный аксикон

Комплексную функцию пропускания рефракционного аксикона можно представить в следующем виде:

т (г) = exp( ik a ₀ r ),

где k =2π / λ – волновое число, λ – длина волны, α 0 – параметр, равный синусу угла выходящих лучей и зависящий от материала аксикона и угла при его вершине.

Для дифракционного аксикона с непрерывным (без учёта скачков величиной 2π) изменением фазы выражение (1) сохраняет силу, но здесь α 0 может быть и больше единицы.

Ниже будем рассматривать действие наиболее простой реализации в виде бинарного дифракционного аксикона с числовой апертурой NA=0,95 (период решетки 1,05λ), у которого фаза принимает значения 0 и π радиан. Высота рельефа бинарного элемента, соответствующая фазе π радиан, при показателе преломления материала элемента n = 1,5 равна:

h = —^П— = X . k ( n - 1)

В дальнейшем высота рельефа h дифракционного аксикона будет варьироваться от 0,25λ до 3λ.

Следует отметить, что вполне можно ожидать, что результат расчёта по строгой электромагнитной теории будет заметно отличаться от результатов, полученных на основе геометрической оптики или в модели тонкого элемента по формулам Кирхгофа. Более точно можно сказать следующее. В рамках геометрооптического подхода бинарный элемент при нормальном падении пучка вообще не изменяет падающий пучок независимо от высоты рельефа. При использовании интеграла Кирхгофа (как в скалярном, так и в векторном варианте) учитывается только набег фазы, создаваемый элементом, продольный размер которого считается достаточно малым.

Иногда для лазерных пучков требуется равномерное распределение интенсивности по сечению пучка, чего можно добиться, используя пучки с распределением амплитуды, аппроксимируемым супергауссовой функцией [27, 28]. Также супергауссовые пучки характеризуются более резким спадом интенсивности на краях пучка. Ранее было продемонстрировано преобразование Гауссовых пучков в супергауссовы пучки с использованием DMD (digital micro-mirror device) [28].

Также ранее было показано [20, 29], что добавление оптического вихря существенно меняет фокальную картину и важным становится направление вращения круговой поляризации. При втором порядке оптического вихря и выше для круговой «–» поляризации (знак круговой поляризации противоположен знаку внесенной вихревой фазовой сингулярности)

происходило формирование теневого круглого светового пятна. По этой причине в данной работе рассматривается первый порядок оптического вихря в падающем пучке.

Таким образом, в качестве входного лазерного излучения рассматривались моды Лагерра–супергаусса (1,0), а также супергауссов пучок с радиальной и круговой «–» поляризацией (рис. 1). Размер пучка σ везде указан в мкм. Амплитуда супергауссова пучка степени p определяется выражением

A ( r ) = exp

rp

2 g p

а амплитуда моды Лагерра–супергаусса (1,0) выражением

A ( r , ф ) = r ■ exp

rp

2 g ^p

■ e^ .

Рис. 1. Входные пучки, общая интенсивность: супергауссов пучок (а), (в), мода Лагерра–супергаусса (1,0) (б),(г)

2.    Исследование дифракции супергауссова пучка при изменении высоты аксикона

Параметры моделирования: длина волны X = 0,532 мкм, размер вычислительной ячейки x,y,z е [-5,64 X ; 5,64 X ]. Шаг выборки по пространству - X /16, шаг по времени - X / (32 c ), где c - скорость света. Толщина поглощающего слоя PML~1,13 X . В качестве входного лазерного излучения рассматривался супергауссов пучок степени 6 с радиальной и круговой «–» поляризацией. В табл. 1 показаны результаты исследований для рассматриваемого аксикона при высоте рельефа элемента h от 0,25λ до 3λ.

Табл. 1. Двумерная картина дифракции супергауссова пучка на аксиконе с переменной высотой в плоскости xz, общая интенсивность (размер области 13,5Х х 13,5Х)

Высота h	Круговая «–» поляризация		Радиальная поляризация
	σ = 5 мкм	σ = 12,25 мкм	σ = 5 мкм	σ = 12,25 мкм
0,25λ	7 '        4   8   8 10 12 8    / ■ П 4 6 ' 8 ' 1'о' 12 X     кг г— l ’ 4 ’ 6 ’ 8 10 12 X 8. i— ' 4 ' 6 ' 8 ' 10 ’ 12 X 3'        1                                                    3"        1                                                    3'        1                                                    3' 1 .          1                                                     5:        1                                                     -          1                                                     •          1 ■.. 1. 1.                                                            . 1                                                             ■. 1 7 .    '                                           7. 1 4 1 5 •    ■                             7 .      1"^*                                    7.      l1-^* .    1                              .    1                                   1                              .1 9-1                        9 -    1                        9    1                        9    1 .               1                                                                                                 .              1                                                                                                  .              1                                                                                                 .              1 11 ■      1                              11 •     1                              11 ■     1                              11-1 ■               )                                                                                                 '              ]                                                                                                                 ]                                                                                                                 1 - "^ .        4 ' 6 ' 8 ' 10 ' 12 X У        4 ' 6 ' 8 ' 10 ' 12 X у        4 6   8 Ю ' 12 X У        4 ' 6 ' 8 ' 10 ' 12 X 5       3                                   5 ■                                           5 ■                                            5 .       3                                               .       3                                                .       3                                               .       3 7 -   -1*”                7-   3*                 у. * 3—                 у. - 3 —- ,      3                                          .      3                                          .      3                                                 3 9-3                      9-   3                      9.    3                      9    3 .       3                                               .       3                                                .       3                                               .       3 // ■ з                                      // - з                                      // •      3                                      7/ -       3 ■       3                                               ■       3                                                •       3                                                       3 —[—.7 6   8 10 12 X j.i ,_4 6 8 10 12 X           4 6   8 10 12 X      — v 6 8 10 12 X 3                                                                           3                                     3 5                                                                     5                                  5 7-                             7-   ^ —                    7-   =|'—*                   7- 9'^                 9 ■                      9 ■                      9 11 ■      =1                               11 ■      =1                              77      =1                              77 ■     =1 7 4 — ___________ ' 6 ' 8 ' 10 ' 12 X у Г—14 ‘ 6 ‘ 8 ' 10 ' 12 X   У [—у— ' 6 ' 8 ' 10 ‘ 12 X у г—-4 ' 6 ‘ 8 " 10 ' 12 X 5                                                 5 ■                                                5                                                 5 ■ у.  ^*             7 ■  ^ *              7 •  ^^^            7 ■  ^^^^ 9    ^                   9                          9                          9 И ■     =1                         77 ■    =3                         77     =1                         77 ■    —3 73 ■ — _____________ В • — _____________ В ■ — _____________ В • — _____________ ^ .    1 ^ ' 6 ' 8 ' io' 12 X У [— |—7-, ' 6 ' 8 ' 10 ' 12 X у [— ]—7-, ' 6 ' 8 ' 10 ' 12 X У ГТ—^ 6 ' 8 ' 10 ' 12 X 3'        ------1                                       3"        ------1                                       3          -------1                                                         1 5 ■      —3                            5"                                       5 ■      -----'                            5 ■       ' 7:    ^         7: ^"                         ^ 9-  =1                д.  =1                9.  =1                9.  =1 77 ■           1                              77 ■           1                              77 ■           1                               11 ■      =1 13 ■ —    ' ___________________ 13 ■ —    ' ___________________ 13 ■ —    ' ___________________ 13 ■ —    ' ___________________ . |— 1—7—, 6    8 ' !0 ’ 12 X   у     1—7—, 6 ' 8 ' 10 ' 1'2 X    8. [— 1—7—, 6 ’ 8 ' io ' 1'2 X    8 . i— 1_7_ 6 ' 8 ' 10 ' 12 X 3          ____________1                                        3          ____________1                                        3          ____________1                                        3          ____________1 5-       ----------1                                                         1                                    5-       ----------'                                   5-       ----------' J1                                                                            .                                     1.________                                                             ■ .              _____________________1                                                                       ‘                                         1 у. '     -- 1 »               /.                                  --- _1—                 7.   -----1— .              _____________________)                                                                            .              _____________________}                                                                            .              _____________________1                                                                            .               _____________________J 9.      --------1                            9.     --------1                            9.     --------1                            9.      --------1 .                   ____________________________1                                                                                                      .                   ____________________________1                                                                                                                                                        1                                                                                                      .                   ____________________________1 77 ■        ____________।                                       77 ■        ____________ 1                                       77 •        ____________।                                       77 ■        ____________ 1 •                    ____________________________1                                                                                                                                                        1                                                                                                                                                         1                                                                                                                                                         1 В \ —    __________ 73 ^ —    __________ В - ---------- 73 ^ —    __________
0,5λ
λ
1,25λ
2λ
3λ

Первоначальные исследования при меньшем размере вычислительной ячейки, а также ранее проведенные исследования [1, 10] показали, что шаг выборки по пространству является достаточным.

Следует отметить случай круговой «–» поляризации для высоты рельефа аксикона h =3λ: в непосредственной близости от элемента наблюдается резкое падение интенсивности на оптической оси с последующим восстановлением и формированием боковых «лепестков».

Размер фокального пятна на оптической оси оценивался по полуширине полуспада интенсивности (full width at half maximum – FWHM), длина светового отрезка оценивалась также по полуспаду интенсивности (depth of focus – DOF).

Результаты по FWHM для круговой «–» поляризации приведены в табл. 2, для радиальной поляризации – в табл. 3.

Табл. 2. FWHM при круговой «-» поляризации

Высота h	σ =5 мкм	σ = 12,25 мкм
0,25λ	FWHM = 0,73λ	FWHM = 0,71λ
0,5λ	FWHM = 0,62λ	FWHM = 0,61λ
λ	FWHM=0,7λ	FWHM = 0,72λ
1,25λ	FWHM = 0,77λ	FWHM = 0,83λ
1,5λ	FWHM = 0,91λ	FWHM = 0,85λ
2λ	FWHM=0,54λ	FWHM = 0,47λ
3λ	FWHM = 0,85λ	FWHM = 0,92λ

Все основные максимумы формируются вне оптического элемента. Следует отметить, что для круговой «-» поляризации при h <  X уширение входного пучка не оказывает заметного влияния, но для h = 1,25λ для σ =5 мкм размер фокального пятна меньше на 7,2% по сравнению σ = 12,25 мкм. Для случая h = 1,5λ и σ = 5 мкм основной максимум формируется внутри элемента на расстоянии 0,37λ от края рельефа и начинается резкое падение интенсивности, при выходе из элемента интенсивность лазерного пучка составляет 57% от максимальной. Первый максимум вне рельефа в этом случае формируется на расстоянии 1,4λ от ак-сикона (54% от максимальной интенсивности) с размером фокального пятна FWHM = 0,91λ. Отдельно стоит отметить случай h = 2λ: для лазерного пучка с σ = 12,25 мкм в непосредственной близости от оптического элемента было получено на 12,9% меньшее фокальное пятно (FWHM = 0,47λ) по сравнению со случаем σ = 5 мкм (FWHM = 0,54λ). Для последнего случая основные максимумы формируются внутри аксикона, а первый максимум вне элемента наблюдается на расстоянии 0,86λ от края рельефа. При дальнейшем увеличении высоты h наблюдается уширение фокального пятна в обоих рассмотренных случаях ( h = 3λ).

Также стоит отметить, что в общем случае наблюдались сопоставимые размеры фокальных отрезков для обоих пучков. В частности, для входного пучка с σ =5 мкм максимальный световой отрезок составлял DOF = 2,33λ для h = 1,25λ, а минимальная длина со- ставляла DOF= 1,13λ при h =2λ. Для входного пучка с σ = 12,25 мкм максимальный размер световой иглы был равен DOF = 2,49λ при h = 1,5λ, минимальный размер составлял DOF= 1,06λ при h =3λ.

Табл. 3. FWHM при радиальной поляризации

Высота h	σ =5 мкм	σ = 12,25 мкм
0,25λ	FWHM=0,46λ	FWHM = 0,46λ
0,5λ	FWHM=0,45λ	FWHM = 0,44λ
λ	FWHM=0,47λ	FWHM=0,45λ
1,25λ	FWHM=0,48λ	FWHM = 0,46λ
1,5λ	FWHM=0,55λ	FWHM = 0,46λ
2λ	FWHM=0,4λ	FWHM=0,37λ
3λ	FWHM=0,48λ	FWHM = 0,46λ

Далее приведен аналогичный анализ для радиальной поляризации. Следует отметить, что для случаев h < 1,25 X размеры фокальных пятен для обоих рассматриваемых входных пучков сопоставимы. Для h = 0,5 X наблюдается локальный минимум в значении FWHM по сравнению с h = 0,25λ, h = λ и h = 1,25λ: 0,45λ (σ = 5 мкм) и 0,44λ (σ = 12,25 мкм) соответственно. Далее при h = 1,5λ для более узкого входного пучка наблюдается его уширение в максимуме: лазерный пучок с σ = 12,25 мкм меньше на 16,4 % (0,46λ и 0,55λ). Как и для круговой «–» поляризации, отдельным случаем является h = 2λ. Для радиальной поляризации также наблюдается лучшая фокусировка и минимальный размер фокальных пятен: FWHM = 0,4λ (σ = 5 мкм) и FWHM = 0,37λ (σ = 12,25 мкм). Дальнейшее увеличение рельефа приводит к уширению размера фокального пятна.

Резкая фокусировка, которая наблюдается для h = 2λ, приводит к минимизации размеров световых отрезков на оптической оси: DOF = 0,62λ (σ = 5 мкм) и DOF = 0,58λ (σ = 12,25 мкм). Максимальное значение для обоих пучков было получено при h = 1,5λ: DOF = 2,69λ (σ = 5 мкм) и DOF = 2,97λ (σ = 12,25 мкм).

На рис. 2 приведены поперечные картины дифракции супергауссова пучка с σ = 5 мкм в точке максимальной интенсивности на оптической оси для h = λ и h = 2λ.

Следует отметить, что для радиальной поляризации размер фокальных пятен в максимуме интенсивности более стабилен по сравнению с круговой «–» поляризацией. Лучший результат также получен при h = 2λ и лучше результата круговой «–» поляризации на 25,9 % для лазерного пучка с σ = 5 мкм и на 21,3 % для лазерного пучка с σ = 12,25 мкм.

На рис. 3 показана двумерная картина дифракции супергауссова пучка при h = 0, то есть при отсутствии рельефа элемента.

Как и предполагалось выше, результат качественно отличается от результатов, полученных на основе геометрооптического подхода или по интегральным формулам Кирхгофа. Отличие от геометрооптического рассмотрения очевидно (иначе бы сохранилось исходное распределение). Расчёты по формулам Кирхгофа непосредственно не проводи- лись, поэтому сравнение производится косвенным образом. В модели тонкого элемента, если разность высот рельефа кратна 2λ, то набег фазы и, соответственно, входное поле будет одинаковым. Поэтому при использовании формул Кирхгофа оно осталось бы одинаковым и при дальнейшем распространении, чего мы не наблюдаем (сравните рисунки для h = λ и h = 3λ). Рисунок для h =2λ тоже подтверждает различие: он должен был совпасть с результатом для h = 0 (рис. 3), то есть распределением амплитуды при прохождении пучка через отверстие в экране (пинхол).

Круговая поляризация

Радиальная поляризация

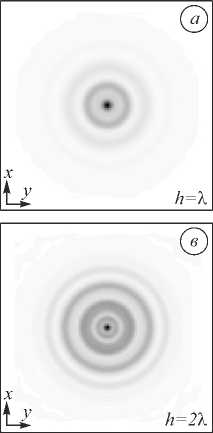
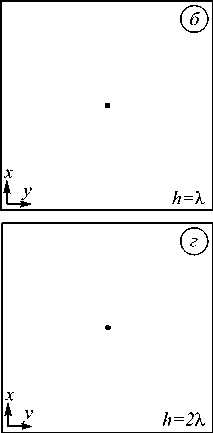
Рис. 2. Двумерная картина дифракции супергауссова пучка (общая интенсивность) в плоскости xy на аксиконе с высотой h = λ (а), (б) и h = 2λ (в), (г)

Супергауссов пучок

Мода Лагерра-суперГаусса

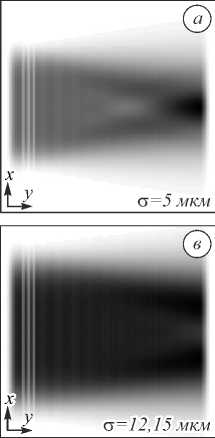
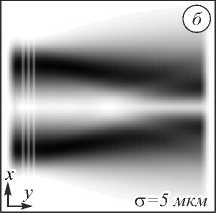
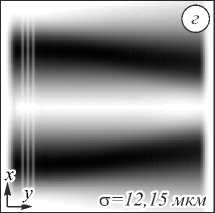
Рис. 3. Двумерная картина дифракции

(общая интенсивность) в плоскости xz при отсутствии рельефа для (а), (в) супергауссова пучка, (б),(г) моды Лагерра–супергаусса (1,0)

3.    Исследование дифракции мод Лагерра– супергаусса (1,0) при изменении высоты аксикона

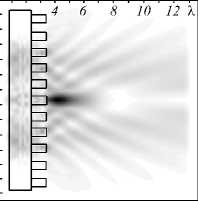
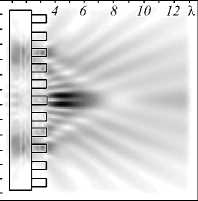
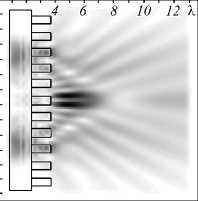
В данном параграфе продолжаются исследования влияния изменения высоты рельефа аксикона на картину дифракции в ближней зоне. Параметры моделирования аналогичны предыдущему параграфу. В качестве входных лазерных пучков рассматриваются моды Лагерра–супергаусса (1,0) с радиальной и круговой «–» поляризацией. В табл. 4 приведены результаты распространения рассматриваемого лазерного излучения через дифракционный аксикон с высотой рельефа h от 0,25λ до 3λ.

На оптической оси происходит формирование светового отрезка только в случае круговой «–» поляризации, для радиальной поляризации наблюдается перераспределение энергии в боковые «лепестки», но на расстоянии, большем длины волны от рельефа ак-сикона, можно наблюдать формирование широкого светового отрезка меньшей интенсивности на оптической оси (3 столбец табл. 4).

Увеличение высоты рельефа неравномерно влияет на длину световых отрезков и их форму, особенно это заметно для случая круговой «–» поляризации: для высот 0,25λ ≤ h < λ, а также h > 1,25λ наблюдается падение интенсивности светового отрезка на оптической оси и «разделение» на два симметричных относительно данной оси боковых световых отрезка, наблюдается некоторого рода «вилка» с двумя «зубцами».

Размеры фокальных пятен по FWHM для круговой «–» поляризации приведены в табл. 5. Все пятна формируются за пределами оптического элемента.

Следует отметить, что наименьший размер фокальный пятен по FWHM был получен для h = 0,25λ: 0,37λ (σ = 5 мкм) и 0,4λ (σ = 12,25 мкм). Однако данный результат был получен в непосредственной близости (0,3λ) от аксикона. В дальнейшем наблюдается уширение фокального пятна до 0,92λ при h = 0,5λ. Затем для обоих лазерных пучков наблюдается усиление фокусировки вплоть до h = 1,25λ. В этом случае с помощью лазерного пучка с σ = 12,25 мкм можно получить на 15,8% меньшее по FWHM фокальное пятно, чем для лазерного пучка с σ = 5 мкм (FWHM = 0,48λ и FWHM = 0,57λ соответственно).

Далее наблюдается уширение фокального пятна, несмотря на более резкую фокусировку при h = 2λ. При этом значении высоты рельефа длина полученных фокальных отрезков минимальна: DOF = 0,62λ (σ = 5 мкм) и DOF = 0,65λ (σ = 12,25 мкм). При h = 3λ наблюдается формирование мощной световой иглы как для лазерного пучка с σ = 5 мкм (FWHM = 0,58λ и DOF = 1,44λ), так и для лазерного пучка с σ = 12,25 мкм (FWHM = 0,55λ и DOF = 2,04λ). Также следует отметить сопоставимые значения по FWHM для случая σ = 5 мкм при h = 1,25λ и h = 3λ.

Максимальные значения по DOF были получены для высоты h = 1,5λ как для лазерного пучка с σ = 5 мкм (DOF = 2,79λ), так и для лазерного пучка с σ = 12,25 мкм (DOF = 3,01λ).

Табл. 4. Двумерная картина дифракции мод Лагерра–супергаусса (1,0) на аксиконе с переменной высотой высотой в плоскости xz, общая интенсивность (размер области 13,5Х х 13,5Х)

Высота

h

0,25λ

0,5λ

Круговая «–» поляризация

σ =5 мкм

Радиальная поляризация

σ = 12,25 мкм

σ =5 мкм

σ = 12,25 мкм

	X 1
	3
	5
λ	7
	9
	11
	13

1,25λ

2λ

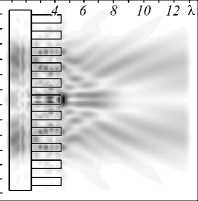
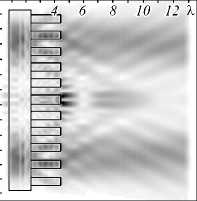
3λ

Табл. 5. FWHM при круговой «-» поляризации

Высота h	σ =5 мкм	σ = 12,25 мкм
0,25λ	FWHM = 0,37λ	FWHM=0,4λ
0,5λ	FWHM = 0,92λ	FWHM = 0,91λ
λ	FWHM = 0,77λ	FWHM=0,79λ
1,25λ	FWHM = 0,57λ	FWHM = 0,48λ
1,5λ	FWHM = 0,63λ	FWHM = 0,5λ
2λ	FWHM = 0,83λ	FWHM = 0,75λ
3λ	FWHM = 0,58λ	FWHM = 0,55λ

На рис. 4 приведены поперечные картины дифракции моды Лагерра–супергаусса (1,0) с σ = 5 мкм для случаев из табл. 5 при h = 0,25λ и h = λ.

Рис. 4. Двумерная картина дифракции моды Лагерра – супергаусса (1,0) (общая интенсивность) в плоскости xy на аксиконе с высотой h = 0,25λ (а) и h = λ (б)

Следует отметить, что по сравнению с супергауссовым пучком с круговой «–» поляризацией для мод Лагерра – супергаусса (1,0) с аналогичной поляризацией меньший размер фокальных пятен по FWHM вне элемента был получен для случаев h = 0,25λ, h = 1,25λ, h = 1,5λ и h = 3λ.

Заключение

Моделирование методом конечных разностей во временной области показало, что изменение высоты дифракционного аксикона существенным образом влияет на дифракционную картину в ближней зоне аксикона. Высота рельефа оптического элемента менялась от 0,25λ до 3λ.

В качестве входного лазерного излучения (ширина пучков σ = 5 мкм и σ = 12,25 мкм) рассматривались моды Лагерра–супергаусса (1,0), а также супергауссов пучок с радиальной и круговой поляризацией.

Анализ картины интенсивности электрического поля показал, что наименьший размер фокального пятна для супергауссова пучка был получен при радиальной поляризации и размере пучка σ = 12,25 мкм: FWHM = 0,37λ при h = 2λ, что лучше результата круговой «–» поляризации на 25,9% для лазерного пучка с σ = 5 мкм и на 21,3 % для лазерного пучка с σ = 12,25 мкм. Минимальный размер фокального пятна для моды Лагерра–супергаусса (1,0) получен для круговой «–» поляризации и размере пучка σ = 5 мкм: FWHM = 0,37λ при h = 0,25λ. Для супергауссова пучка при аналогичном виде поляризации минимальное фокальное пятно FWHM = 0,47λ (σ = 12,25 мкм) при h = 2λ.

Наиболее протяженный световой отрезок на оптической оси был получен для моды Лагерра– супергаусса (1,0) с круговой «–» поляризацией и σ = 12,25 мкм: DOF = 3,01λ при h = 1,5. Для супергауссова пучка максимальная длина была получена для радиальной поляризации при h = 1,5λ: DOF = 2,97λ (σ = 12,25 мкм).

Работа выполнена при поддержке Российского научного фонда (проект № 20-72-00051) в частях «Исследование дифракции супергауссова пучка при изменении высоты аксикона», «Исследование дифракции мод Лагерра–супергаусса (1,0) при изменении высоты аксикона», «Заключение», Министерства науки и высшего образования в рамках выполнения Государственного задания (проект № 0777-20200017) в части «Прохождение супергауссовых пучков через бинарный дифракционный аксикон», а также в рамках выполнения работ по Государственному заданию ФНИЦ «Кристаллография и фотоника» РАН (соглашение № 007-ГЗ/Ч3363/26) в части «Введение».