Исследование особенностей распространения линейно-частотно-модулированных сигналов в двухслоевой анизотропной ионосфере с пространственной модуляцией

Настоящая работа посвящена математическому моделированию распространения электромагнитных волн в средах с дисперсией [1; 2]. В основе нашего подхода к проблеме описания распространения радиосигналов в ионосфере Земли лежат лучевые методы, являющиеся традиционными при описании процессов распространения декаметровых радиоволн в различных средах (см., например [3; 5]).

При моделировании лучевых траекторий в анизотропной, неоднородной, нестационарной плазме бихарактеристическая система уравнений с гамильтонианом имеет вид [6]:

r= kx + k² + k²-^ ^e( r, ^r ® )

dr = дГ dk = дГ dt = дГ d го = дГ dт дk , dт дr , dт дго , dт дt ’

где ^r = ( x, y, z ) - координаты точки наблюдения, k = ( kx , ky , kz ) - волновой вектор, ω – круговая частота излучения, t – групповое время, τ – параметр вдоль лучевой

——

траектории, с = 2,997925'10 '0 м/с - скорость света, е ( ^— , к , ю ) - эффективная диэлектрическая проницаемость среды.

Эффективная диэлектрическая проницаемость среды для неоднородной анизотропной ионосферы имеет вид (см., например [7]):

2 v (1 - v )

• ± = 1--।                                 =

2(1 - v ) - u sin ² a ± uu ² sin ⁴ a + 4 u (1 - v ) ² cos ² a

Знак «+» соответствует обыкновенной волне, а знак «–» – необыкновенной волне. Параметр v является отношением квадрата плазменной частоты к квадрату рабочей частоты:

v =

co | = 4 n e ² N (to J      me to ²

В формуле (4) e = 4,8029 10^-10 СГСЭ - заряд электрона, m_e = 9,108 10^-28 г - масса электрона, N – величина электронной концентрации в фиксированной точке пространства. В выражении (3) величина u – это отношение квадрата гирочастоты частоты к квадрату рабочей частоты:

( ю_н ' '     e ² H²

u = ---- I = 2 2 2 ,

^ ю J   mec ю а величина a - это угол между волновым вектором и напряженностью магнитного поля Земли H0 = (H0x, H0y, H0z). Выражение для квадрата косинуса угла а, необходимое для применения формулы (3), имеет вид:

cos ² а =

( H о xkx + H о yky + H о zkz ) 2 H0\Ц 2

В приведённых ниже расчетах амплитуда магнитного поля предполагается постоянной, а ориентация напряжённости магнитного поля относительно локальной системы координат задается двумя углами γ и φ:

H0x = H0cos Ycos ф, H0y = H0cos ysin ф, H0z = H0sin Y•(5)

Предположим, что начальный волновой вектор k (0) параметрически зависит от угла выхода луча α₀.

kx (0) = — a/s0 cos a0, к (0) = 0, kz (0) = — Je0 sin a0.(6)

cc

Источник излучения – точечный, он находится вне магнитоактивной плазмы и расположен в точке с координатами r11=0 = (0, 0, 0).(7)

Величина ε0 в выражениях (6) – это значение эффективной диэлектрической проницаемости среды в источнике излучения. Лучевая структура сигнала при изменении высоты источника излучения рассматривалась в работе [8].

Будем считать, что сигнал линейно-частотно-модулированный (ЛЧМ), то есть формула для мгновенной частоты заполнения имеет вид [9]:

— (0) = — o (1 + Sn ) , t (0) = n , f ( t ) = f , ( 1 + 8 1 ) ,                    (8)

где η – начальное время выхода луча, f ₀ – начальная частота (Гц). В данной работе были приняты следующие значения параметров: T_и –длительность импульса (с)

( Т и = 2,79 с), 5 =1 с^-1. Распространение электромагнитной волны изначально осуществляется в плоскости ( x , z ).

Модель ионосферной плазмы – двухслойная. Предполагается, что профиль электронной концентрации имеет вид [3–4]:

N (г ) = Nо'

1 Nr exp₂

exp(-0)

1 -0--^—2 + р exp

cos X

z ^- z 02

V zm 2

N_r = 1 + p sin

' x_ )   A _ z - z 01

I ’ ⁰                    .

V X )       zm 1/²

В выражении (9) z ₀₁ – высота максимума слоя F ₂, z_{m 1} – условная полутолщина слоя F ₂, β – безразмерный коэффициент, характеризующий степень ионизации нижнего слоя по отношению к основному, z ₀₂ – высота максимума нижнего слоя E , z_{m 2} – условная полутолщина нижнего слоя E , N ₀ – электронная концентрация в максимуме основного слоя F ₂, если р = 0 . Максимум ионосферного слоя F ₂ модулируется периодической функцией N_r .

При вычислении применялись следующие значения параметров: N 0 = 2 10 6 см ^{- 3}, Н 0 = 0,36 Э, Z 1 = 140 км, Z 01 = 300 км, Z 2 = 40 км, Z ₀₂ = 100 км, Z = 0, Y = 135 ° , Ф = = 90 ° , р = 0,1, х = 0, p = 0,1, x_r = 25 км.

Численное моделирование лучевой структуры

Рассмотрим результаты численного моделирования (см. также работы [10–12]), в которых проводились аналогичные исследования). На рис. 1 показана лучевая структура ЛЧМ радиосигнала в случае распространения в плоскости ( x , z ), когда источник находится на Земле (высота источника излучения – 0 км). Уровень максимальной высоты распространения луча соответствует частоте излучения. Угол выхода лучей – 90° по отношению к горизонтали. Линиями равного уровня на рисунках показана электронная концентрация ионосферы. В районе 100 км по высоте просматривается слой Е . На высоте 300 км хорошо виден слой F ₂ и его пространственная модуляция. Каждый луч соответствует определенной частоте излучения. Сначала все лучи идут по общей вертикальной траектории. В диспергирующей среде (ионосфере) они расходятся. Низкочастотные лучи отражаются от слоя F ₂ и возвращаются на Землю, а высокочастотные просачиваются сквозь слой. Чем выше частота, тем глубже проникает луч в ионосферный слой.

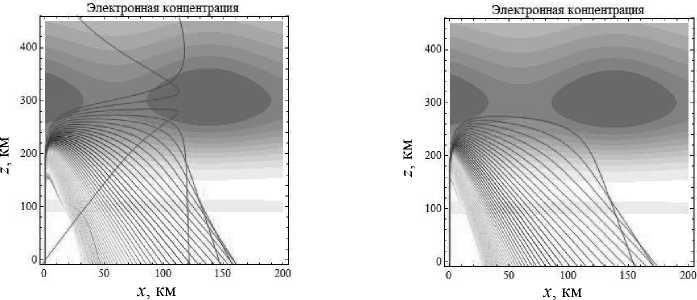
Рис. 1б

Лучевые структуры ЛЧМ радиосигнала в плоскости ( x , z ), начальная частота источника излучения 3,5 МГц. Рис. 1а – обыкновенная волна, рис. 1б – необыкновенная волна. Угол выхода – 90°

Рис. 1а

Выбрав начальную частоту излучения f ₀ = 3,5 и изменив угол выхода луча (45°), видим, что в плоскости ( x , z ) лучи даже не доходят до слоя F ₂ (рис. 2). В случае обыкновенной волны (рис. 2а) луч средней частоты остаётся в межслоевом канале. Необыкновенная волна, повторяя траекторию обыкновенной волны, просачивается на обратном пути сквозь слой Е , как показано на рис. 2б.

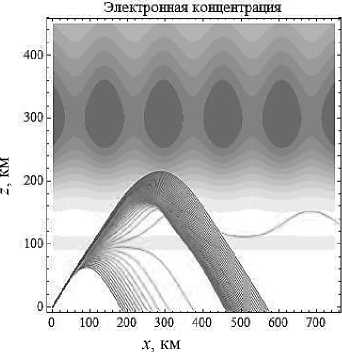
Рис. 2а

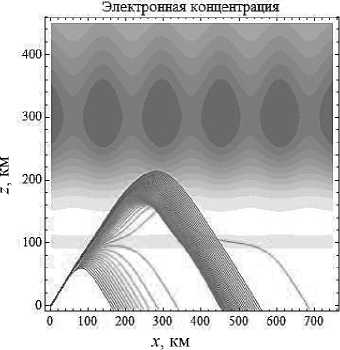
Рис. 2б

Лучевые структуры ЛЧМ радиосигнала в плоскости ( x , z ), начальная частота источника излучения – 3,5 МГц. Рис. 2а - обыкновенная волна, рис. 2б - необыкновенная волна. Угол выхода – 45°

Анализ взаимодействия слоя F ₂ и семейства лучей с начальной частотой f ₀ = 5 МГц и углом выхода 90° показывает нам, что бóльшие частоты просачиваются сквозь слой и не возвращаются обратно, а меньшие, частично меняя свою траекторию, возвращаются (рис. 3). Сравнивая рис. 1 и рис. 3 с одним и тем же углом выхода, но разницей в начальной частоте 1,5 МГц, выясняем, что эта разница отражается в количестве лучей как прошедших все ионосферные слои, так и не прошедших слой E .

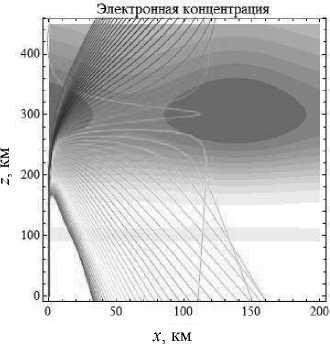
Рис. 3а

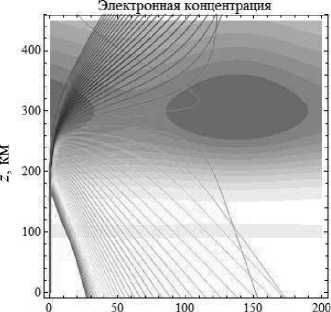
x , км

Рис. 3б

Лучевые структуры ЛЧМ радиосигнала в плоскости ( x , z ), начальная частота источника излучения – 5 МГц. Рис. 3а - обыкновенная волна, рис. 3б - необыкновенная волна. Угол выхода – 90°

Рисунок 4 показывает нам, что лучи, выходящие под углом 45°, с увеличением начальной частоты теперь доходят до слоя F ₂ и, взаимодействуя с ним, частично просачиваются в более высокие слои. На рис. 2 мы видим другую ситуацию.

Необыкновенная волна, повторяя траекторию обыкновенной, оставляет часть средних частот в межслоевом канале, что, судя по рисунку, нельзя сказать про обыкновенную волну. Это объясняется тем, что у обыкновенной и необыкновенной волн имеются отличия в скорости и направлении распространения.

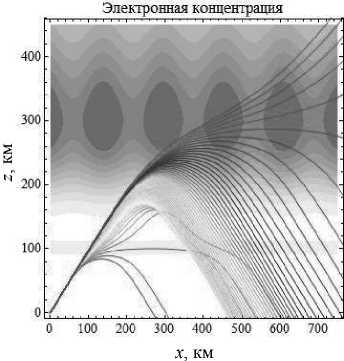
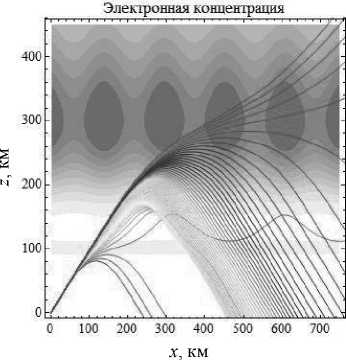
Рис. 4б

Рис. 4а

Лучевые структуры ЛЧМ радиосигнала в плоскости ( x , z ), начальная частота источника излучения – 5 МГц. Рис. 4а - обыкновенная волна, рис. 4б - необыкновенная волна. Угол выхода – 45°

Увеличивая начальную мгновенную частоту ещё на 1,5 МГц при угле выхода лучей 90°, получаем лучевую структуру, представленную на рис. 5. Видим, что теперь количество частот, не проходящих слой E , стало гораздо меньше. Если сравнивать

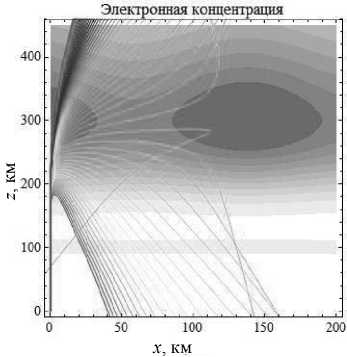
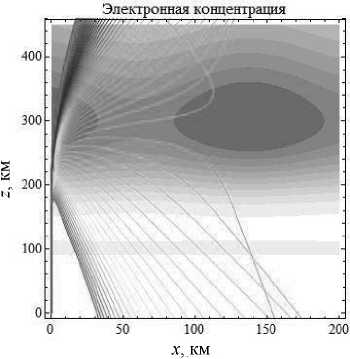
Рис. 5б

Рис. 5а

Лучевые структуры ЛЧМ радиосигнала в плоскости (x, z), начальная частота источника излучения – 6,5 МГц. Рис. 5а - обыкновенная волна, рис. 5б - необыкновенная волна. Угол выхода – 90° все рисунки с углом выхода 90° (рис. 1, 3, 5), видно, что траектория лучей, имеющих низкую начальную частоту, повторяется. Лучи, имеющие высокую начальную частоту, просачиваются в более высокие слои. Даже если сравнить обыкновенную волну с необыкновенной (рис. 5), ничего особо не изменилось по сравнению с рис. 3 или рис. 1, за исключением увеличения частоты.

Меняя угол выхода луча, можно увидеть, как изменяется траектория луча в слоях E и F ₂. Так, например, на рис. 6 видно, что при увеличении начальной мгновенной частоты до 6,5 МГц все частоты проходят слой Е , чего нельзя сказать о рис. 4. Видно, что малые частоты лучей на рис. 4 определяют качественную разницу между начальной мгновенной частотой 6,5 МГц и 5 МГц.

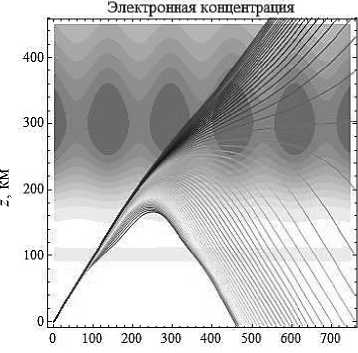
x , км

Рис. 6а

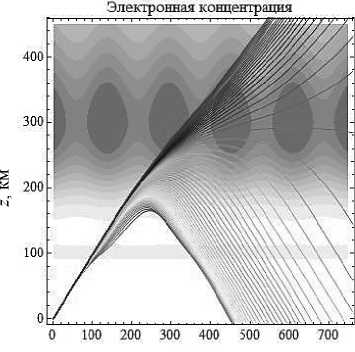
x , км

Рис. 6б

Лучевые структуры ЛЧМ радиосигнала при частоте источника излучения 6,5 МГц в плоскости ( x , z ). Рис. 6а - обыкновенная волна, рис. 6б - необыкновенная волна. Угол выхода – 45°

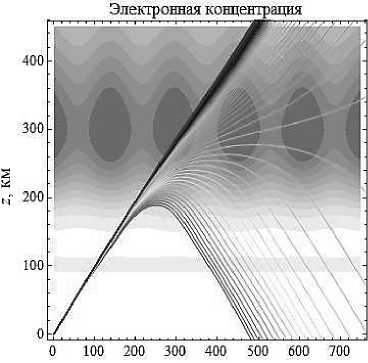
Резко меняя начальную мгновенную частоту с 6,5 МГц на 9,5 МГц (рис. 7), видим, что число лучей, не доходящих до слоя F2, стало гораздо меньше. Это не удивительно, ведь частота стала больше. А это значит, что с увеличением мгновенной частоты при угле выхода лучей 90° существует большая вероятность того, что все лучи пройдут сквозь слой F2 в более высокие слои.

В заключение приведем рис. 8 для начальной частоты f ₀ = 9,5 МГц и при угле выхода лучей 45°. Видно, что рисунок нам начал напоминать структуру при выходе угла 90°.

Заключение

Таким образом, в настоящей работе сопоставлены особенности распространения ЛЧМ сигналов в двухслоевой анизотропной ионосфере при увеличении мгновенной частоты источника в случаях обыкновенной и необыкновенной волн. Рассмотрен ионосферный слой с пространственной модуляцией. Сопоставлены результаты вычислений в случаях обыкновенной и необыкновенной волн. Показано, что лучевая структура необыкновенной волны повторяет лучевую структуру обыкновенной волны в плоскости распространения.

Для расчетов лучевых характеристик применялась бихарактеристическая система дифференциальных уравнений, неизвестными в которой являются координаты луча, компоненты волнового вектора, а также частота и время. Несмотря на значительный объем исследований в данной области, распространение частотно-модулированных

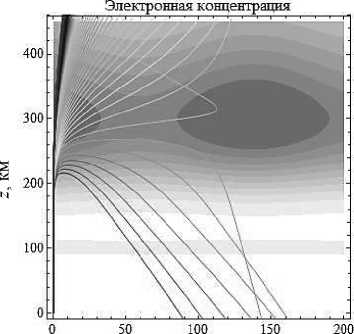
x , км

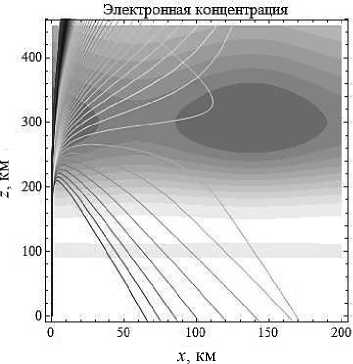
Рис. 7б

Рис. 7а

Лучевые структуры ЛЧМ радиосигнала в плоскости (x, z), начальная частота источника излучения – 9,5 МГц. Рис. 7а - обыкновенная волна, рис. 7б - необыкновенная волна. Угол выхода – 90° сигналов в анизотропной ионосферной плазме изучено ещё недостаточно. При построении бихарактеристик в анизотропной неоднородной ионосферной плазме использовался пакет прикладной программы Wolfram Mathematica, поддерживающей математические символьные вычисления.

Автор выражает благодарность своему научному руководителю Крюковскому Андрею Сергеевичу за ценные советы при планировании и проведении данного исследования, за рекомендации по написанию и оформлению настоящей статьи.

x , км

Рис. 8а

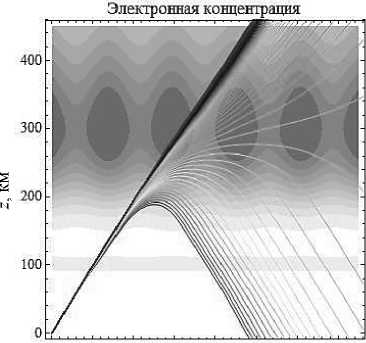
О 100 200 300 400 500 600 700

x , км

Рис. 8б

Лучевые структуры ЛЧМ радиосигнала при частоте источника излучения 9,5 МГц в плоскости ( x , z ). Рис. 8а - обыкновенная волна, рис. 8б - необыкновенная волна. Угол выхода – 45°