Исследование панельного флаттера круговых цилиндрических оболочек, выполненных из функционально-градиентного материала

Функционально-градиентный (ФГ) материал – современный композиционный материал, который состоит из смеси двух или более компонентов, например керамики и металла [1]. По сравнению со слоистыми композитами для таких материалов характерно непрерывное и гладкое изменение механических и физических свойств по толщине конструкции. Улучшенные эксплуатационные характеристики изделий, выполненных из функционально-градиентных материалов, привлекли внимание инженеров из многих отраслей техники, что способствовало появлению обширного ряда работ по исследованию статических и динамических свойств таких конструкций под воздействием механических, температурных или аэродинамических нагрузок [2–16]. В частности, анализ панельного флаттера круговых цилиндрических оболочек, обтекаемых сверхзвуковым потоком газа, представлен в работах [17–18]. В этих работах различными методами исследовано влияние разнообразных консистенций ФГ-материала на границу аэро-упругой устойчивости свободно опертых цилиндрических оболочек, в том числе подвергающихся дополнительному воздействию температурных и механических нагрузок. Детального анализа влияния различных вариантов граничных условий на критические скорости течения газа в этих исследованиях не представлено, поэтому он является предметом исследований в настоящей работе для случая ненагруженных оболочек.

1.    Постановка задачи и метод решения

Рассматривается упругая цилиндрическая оболочка, выполненная из функционально-градиентного материала (рис. 1), длиной L и радиусом R. Оболочка со скоростью U∞ обтекается сверхзвуковым потоком идеального сжимаемого газа. Целью работы является исследование влияния свойств ФГ-материала на границу аэроупругой устойчивости при различных вариантах граничных условий и линейных размерах конструкции.

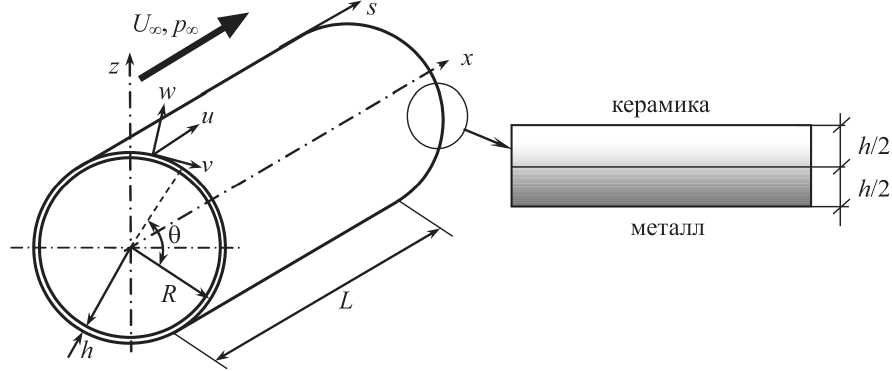
Рис. 1. Цилиндрическая оболочка из функционально-градиентного материала, обтекаемая сверхзвуковым потоком газа

Эффективные физико-механические характеристики оболочки P eff , выполненной из ФГ-материала, определяются свойствами составляющих материалов P и их объемными долями V . В случае функционально-градиентного материала, состоящего из двух материалов,

P f = PV + P 2 V 2 .

Для оболочки постоянной толщины h объемные доли являются функциями радиальной координаты z , отсчитываемой от срединной поверхности, и изменяются согласно степенному закону:

у, (-z+h )^N y_=X_y

V 1 I I , V 2 ¹ V 1 ,

V 2 h )

где N – показатель объемной доли, изменяющийся от нуля до бесконечности. С учетом последнего представления эффектные характеристики, под которыми понимаются модуль упругости E , коэффициент Пуассона v и плотность материала р , вычисляются следующим образом:

N

P^P, + ( P 2 - P i ) ( -h- ) .

Аэродинамическое давление, действующее со стороны потока газа на упругую поверхность, вычисляется согласно квазистатической аэродинамической теории с помощью приближенной формулы [19, 20]

( д w д w    3

Р =- q I     'Qi -— q 2 w I ,

V д s     д t       J где q=p U2/P=Kp~M2/Р, q = q(M2-2)/(U 3'), q2 = q,(2RP)-

Здесь s - меридиональная координата; w - нормальная составляющая вектора перемещения; M = U _м / c _м - число Маха; р_м , p ^ и с ^ - плотность, статическое давление и скорость звука в невозмущенном потоке газа; q - модифицированное динамическое давление; к - показатель , - X1/2

адиабаты; р= ( M - 1 ) -

В [21] показано, что для классической теории оболочек, основанной на гипотезах Кирхгофа-Лява и линейном законе изменения перемещений по толщине оболочки,

U1 = u(s,0)+z01(s,6), U2 = v(s,0)+z02(s,0), U3 = w(s,0), соответствующие геометрические и физические соотношения, а также уравнения движения c учетом разложения в ряд Фурье по окружной координате 0 могут быть сведены к системе восьми обыкновенных дифференциальных уравнений первого порядка относительно следующих неизвестных:

У 1 = T 11 , у 2 = 5 + 2 H / R , у 3 = M 11 , у ₄ = Q 11 + j_RH , У 5 = u , У 6 = v , У 7 = w , У 8 =⁰ 1 -

Здесь s , 0 , z - криволинейные координаты; u ( s , 0 ), v ( s , 0 ) и w ( s , 0 ) -составляющие вектора перемещений срединной поверхности ; 0 1 ( s , 0 ) и 0 ₂ ( s , 0 ) - углы поворота недеформируемой нормали; T = { T 1 , T ₂₂, 5 , M 11 , M ₂₂, H } ^T - вектор усилий и моментов; Q 11 - обобщенная сила; j_R = j / R ; j - номер гармоники при разложении в ряд Фурье-

Система может быть записана следующим образом:

дУ/д5 = f(jЛу) ,(3)

где fi = jR (2 HIR - y 2 )-X 2Po У 5, f2 = jT — Q22IR —X2POУ6’ f3 = У4 — 2jRH,(4)

f4 — T22 1R — j RQ22 -X poy7 + qy8 + (iXq1 — q2 )y7’ f5  £11’ f6  £12 + jRy5’ f7    y8’ fi

Входящие в выражения (4) величины вычисляются по следую щим формулам:

£ 22   ^jRy 6 + y 7 ^{1 R} ’ ^К 22   ^jR ^ 2 ’ ^ 2 y 6 ^{1 R j}Ry 7 ’ ^{H  b} 44 ^ 12 + ² c 44 ^K 12 ’

^K 11   [ a 11 ⁽ y 3 ^b 12 ^£ 22 c 12 ^K 22 ) ^b 11 ⁽ y 1   a 12 ^e 22 ^b 12 ^K 22 ) ] ^{1 (} a 11 c 11 ^b 11

^£ 11   ⁽ y 1   a 12 ^£ 22   ^b 11 ^K 11   ^b 12 ^K 22 )/ a 11 ’ ^T 22   a 12 ^E 11 + a 22 ^E 22 + ^b 12 ^K 11 + ^b 22 ^K 22 ’

M 22 ^b 12 ^E 11 ^{+ b} 22 ^ 22 + c 12 ^K 11 + c 22 ^K 22 ’

^K 12   ^(E 12 + ^jRy 5 ) ^{1 R j}Ry 8 ’

^£ 12 ^— [ У 2 - ² ( ^b 44 ^{+ 2} c 44 ^{1 R} ) j R ( У 5 ^{1 R +} У 8 ) ] ¹ [ a 44 ^{+ 4} k 2 ( ^b 44 ⁺ k 2 c 44 ) ] ’

^Q 22 ^—- j_RM 22 ’ P o ^— J P eff dz ’ ( a j ’ ^b j ’ c j ) ^— J ( ¹’ z ’ z ² ) ^B j dz ’ ⁽ i ’ j ^{— 1}’²’⁴⁾’

B ,1 — B 22 — E ., ¹ ( 1 -V 2,, ). B ,2 — V f Bn, ^B 44 — E„_r ¹²¹ ( 1 + V .ff ) .

Здесь e — { e ₁₁ ’ E ₂₂ ’ E ₁₂ ’ k ₁₁ ’ K ₂₂ ’2 k ₁₂ } ^T - вектор деформаций’ кривизн и кручения; i ² — - 1; X—Х 1 + i X ₂ - характеристический показатель. На краях оболочки задаются следующие однородные граничные условия:

У i L— о ⁵ - -+ у - >4| _s — о ^{( 1 -5} - -^{) — 0}’ i ^{— L} " ⁴’ ⁽⁵⁾

У i L— L ^S i + 4 ⁺ У , + 4| 5 — L ( ^{1 -S} i + 4 ) ^{— 0}’ i ^{— 1} ^ ⁴’ ⁽⁶⁾ где 5 i — 0’ если заданы кинематические’ и 5 i — 1 ’ если заданы статические граничные условия.

Система (3) с граничными условиями (5)-(6) решается методом ортогональной прогонки Годунова с численным интегрированием дифференциальных уравнений методом Рунге-Кутты четвертого порядка точности [22]. Для этих целей общее решение системы (3) представляется в виде

4 y=ECjyj, j । где Cj - некоторые константы и y j - совокупность линейно независимых решений системы (3), удовлетворяющих граничным условиям (5). В результате интегрирования по заданному интервалу и удовлетворения граничных условий (6) получаем следующую алгебраическую систему для определения постоянных Cj:

E C j f j = 0, i = 1,4.                        (7)

j = 1

Решение задачи сводится к вычислению и анализу таких значений параметра X , при которых существует нетривиальное решение системы (7), условием которого является равенство нулю определителя матрицы | f j ( X)| = 0. Для нахождения комплексных собственных значений матрицы f j ( X ) используется итерационный алгоритм, основанный на методе парабол (Мюллера) [23]. В отличие от обычной реализации этого метода, здесь в качестве начальных приближений используются собственные частоты колебаний оболочки в вакууме to при U _м = 0 . Для определения последних используется комбинация шагового метода, посредством которого вычисляются такие значения to , при которых происходит смена знака определителя | f j ( X )| и метода, уточняющего to в полученном диапазоне. В качестве последнего используется метод деления отрезка пополам.

2.    Численные результаты

В численных примерах рассматривается цилиндрическая функционально-градиентная оболочка (h = 1х10-4 м), выполненная из алюминия (внутренняя поверхность) и оксида циркония (наружная поверхность). Физико-механические характеристики составляющих материалов приведены в табл. 1 [2]. Расчеты выполнялись для свободно опертых (v = w = T11 = M 11 = 0, SS) или жестко закрепленных (u = v = w = 01 = 0, CC) на обоих торцах и консольно закрепленных (T, = 0, S+2H/R=0,M,, = 0, О,, + /'H=0, CF) оболочек, обтекаемых по-11                                  11          11 R током газа с параметрами, заимствованными из экспериментальных работ [24, 25]: у = 1,4; M = 3, температура торможения в свободном потоке T„ = 48,89 °C. В представленных ниже расчетах в качестве варьируемой величины используется статическое давление в невозмущенном потоке pте, а для представления результатов вычислений применяется безразмерный параметр динамического давления q = q / Ef х10 7, где Ee1ff – эффективный модуль упругости функционально-градиентного материала, полученный при N = 1.

Таблица 1

Физико-механические свойства составляющих материалов

Материал	E , ГПа	v	р , кг/м3
Алюминий, Al ( N = ^ )	70	0,3	2707
Оксид циркония, ZrO 2 ( N = 0)	151	0,3	3000

С целью тестирования разработанного алгоритма осуществлено сравнение с известными экспериментальными, численно-аналитическими и численными решениями для изотропной оболочки, свободно опертой на обоих торцах и имеющей следующие характеристики: h = 1,016 х 10^-4 м, R = 0,2032 м, р = 8,904 х 10³ кг/м³. Остальные параметры определяют различные варианты расчета: вариант I, L = 0,4064 м, Е = 89,647 ГПа, v = 0,33; вариант II, L = 0,3912 м, Е = 110,31 ГПа, v = 0,35. Сравнение критических номеров гармоник j cr и соответствующих им минимальных значений статического давления в свободном потоке p ^ приведено в табл. 2. Из представленных данных следует, что получаемые в рамках разработанного алгоритма результаты достаточно хорошо согласуются с известными решениями.

Таблица 2

Сравнительные значения границ флаттера для свободно опертой изотропной оболочки

Источник	Вариант	p „ , Па	j cr
Эксперимент [24]	II	2620–2896	20
Аналитическое решение [25]	II	3792	25
Аналитическое решение [26]	I	2896	24
МКЭ [27]	I	3875	34

Окончание табл. 2

Источник	Вариант	p ~ , Па	j cr
МКЭ [27]	I	3875	25
МКЭ [28]	II	3875	26
Комбинированный МКЭ [29]	I	2633	25
Комбинированный МКЭ [29]	II	3599	26
Расчет	I	2744	24
Расчет	II	3713	25

В рассмотренном выше примере, как и в последующих расчетах, потеря устойчивости оболочки осуществляется в виде флаттера по двум формам колебаний. Для демонстрации этого вида неустойчивости на рис. 2 приведены зависимости действительных и мнимых частей двух первых собственных значений X от безразмерного параметра динамического давления q для жестко закрепленной на обоих торцах оболочки. Через m на рисунке обозначено число полуволн в меридиональном направлении. При отсутствии потока газа ( q = 0) собственные частоты являются действительными. При наличии потока газа ( q >  0) собственные значения становятся комплексными. При возрастании давления действительные части двух низших собственных значений начинают сближаться друг с другом и при q ₀ = 4,58 сливаются. При дальнейшем увеличении давления мнимая часть второй моды при q_F = 7,69 меняет знак с положительного на отрицательный, что характеризует начало области аэроупругой неустойчивости.

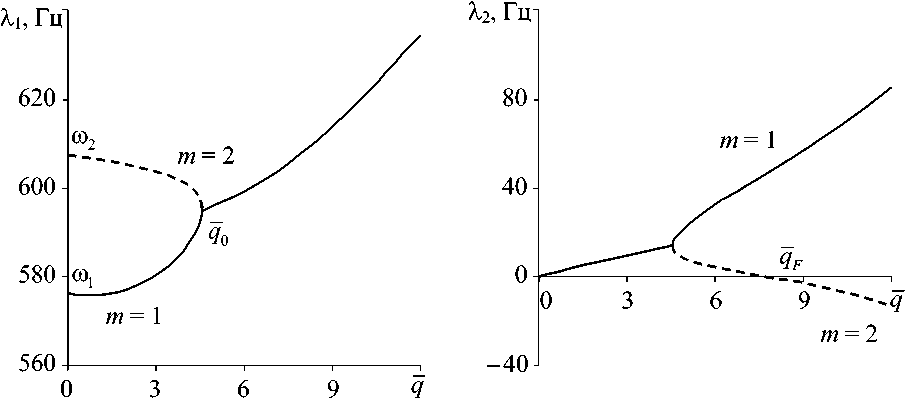
б

а

Рис . 2. Зависимости действительных (а) и мнимых (б) частей двух первых собственных значений X от безразмерного параметра динамического давления q для жестко закрепленной на обоих торцах оболочки: L / R = 4, h / R = 1000, j = 14, N = 1

Из представленного выше соотношения (1) следует, что эффективные характеристики функционально-градиентного материала непрерывно изменяются в зависимости от радиальной координаты z и при z = - h /2 определяются свойствами материала, расположенного на нижней поверхности оболочки, а при z = h /2 - на верхней. Этот вывод демонстрируется данными, представленными на рис. 3. Здесь показаны зависимости объемных фракций составляющих материалов от безразмерной радиальной координаты оболочки z / h для различных значений показателя объемной доли N отдельно для стали и керамики.

На рис. 4 представлены зависимости безразмерного параметра динамического давления q от номера гармоники j при разной величине объемной доли N для оболочек с консольным закреплением (рис. 4, а ) и свободно опертыми краями (рис. 4, б). Из представленных данных следует, что с увеличением объемной доли N границы аэроуп-ругой устойчивости снижаются, поскольку при этом возрастает объем материала, обладающего более низкой жесткостью, а именно металла. При этом критический номер гармоники, т.е. номер гармоники, на котором имеет место минимальное значение безразмерного параметра динамического давления, или, другими словами, форма потери устойчивости, определяются не только геометрическими характеристиками оболочки и заданными граничными условиями, но и заданной консистенцией ФГ-материала.

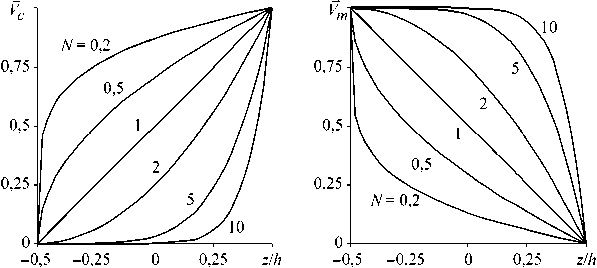
а

б

Рис. 3. Зависимость объемных фракций составляющих материалов V от безразмерной толщины оболочки z / h для различных значений показателя объемной доли N : а - керамика; б - сталь

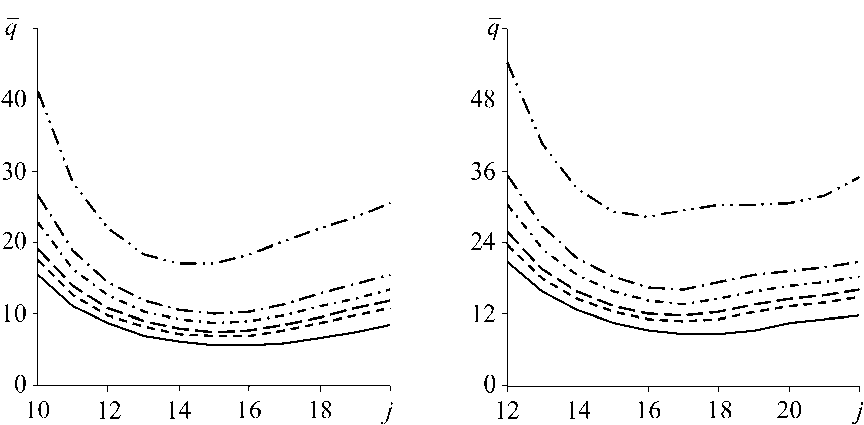
а

б

Рис. 4. Зависимости безразмерного параметра динамического давления q от номера гармоники j при разной величине объемной доли N ; а – консольно закрепленная оболочка; б – свободно опертая оболочка: L / R = 2, h / R = 1000; –––– – Al; –∙–∙ – N = 1;

-∙-∙-∙ – N = 2; – – – – N = 5; ---- – N = 10; –∙∙–∙∙–∙ – ZrO₂

Более детально этот факт демонстрируется посредством данных, представленных в табл. 3, 4. Здесь для оболочек с различными геометрическими размерами и граничными условиями приведены критические номера гармоник j и соответствующие им значения безразмерного параметра динамического давления q , полученные для разных величин объемной доли N при отношении длины оболочки к ее радиусу L / R = 2 (см. табл. 3) и L / R = 5 (см. табл. 4). Из этих таблиц видно, что форма потери устойчивости определяется жесткостью материала оболочки, и в случае ФГ-материала она может отличаться от форм потери устойчивости составляющих материалов. В случае механической нагрузки такая зависимость имеет место для критических значений осевого усилия, тогда как критические значения бокового или гидростатического давлений не зависят от консистенции ФГ-материала и, как показано в [7], определяются только геометрическими размерами оболочки.

Из рассмотренных комбинаций граничных условий именно жестко закрепленные на обоих краях оболочки обеспечивают наибольшую сопротивляемость воздействию сверхзвукового потока газа, особенно в случае толстостенных коротких конструкций. При этом для любого варианта граничных условий критический номер гармоники уменьшается с возрастанием толщины оболочки и ее длины.

Таблица 3

Критические номера гармоник j и значения безразмерного параметра динамического давления q для оболочек с различными геометрическими размерами h / R и граничными условиями (ГУ) в зависимости от разной величины объёмной доли N : L / R = 2

ГУ	h / R	j	ZrO 2	j	N = 1	j	N = 2	j	N = 5	j	N = 10	j	Al
SS	500	14	233,99	15	128,86	15	109,76	15	93,864	15	84,918	13	62,021
	1000	16	28,196	17	16,197	17	13,773	17	11,773	17	10,661	17	8,6703
	2000	22	3,9429	23	2,4854	23	2,1646	23	1,8930	23	1,7341	23	1,4282
CC	500	15	255,73	15	144,17	15	122,19	15	103,75	15	93,394	14	71,969
	1000	18	33,569	18	19,796	18	16,979	18	14,583	18	13,266	19	10,738
	2000	23	4,9606	24	3,1485	24	2,7535	25	2,4089	24	2,2139	25	1,8269
CF	500	13	162,05	11	80,069	11	64,437	11	52,699	11	46,819	12	36,466
	1000	14	16,959	15	10,119	15	8,7356	15	7,5562	15	6,8991	16	5,6523
	2000	19	2,5669	20	1,6505	20	1,4502	20	1,2762	20	1,1757	21	0,9786

Таблица 4

Критические номера гармоник j и значения безразмерного параметра динамического давления q для оболочек с различными геометрическими размерами h / R и граничными условиями (ГУ) в зависимости от разной величины объёмной доли N : L / R = 5

ГУ	h / R	j	ZrO 2	j	N = 1	j	N = 2	j	N = 5	j	N = 10	j	Al
SS	500	10	57,953	11	33,518	11	28,314	11	24,057	11	21,682	9	16,833
	1000	11	8,3415	11	4,6935	11	3,9872	12	3,3552	12	2,9890	12	2,3432
	2000	15	1,1339	15	0,6873	16	0,5885	16	0,5049	16	0,4572	16	0,3699
CC	500	11	67,538	11	38,728	11	32,953	11	28,024	11	25,335	10	20,353
	1000	14	9,6086	13	5,7731	13	4,8758	13	4,1258	13	3,7087	13	2,9612
	2000	16	1,4158	17	0,8626	17	0,7433	17	0,6410	17	0,5839	18	0,4780
CF	500	9	44,241	8	22,209	8	17,913	8	14,595	8	12,845	8	9,8846
	1000	10	4,8231	10	2,8365	10	2,4286	11	2,0708	11	1,8604	11	1,4725
	2000	13	0,6992	14	0,4287	14	0,3714	14	0,3221	14	0,2944	15	0,2424

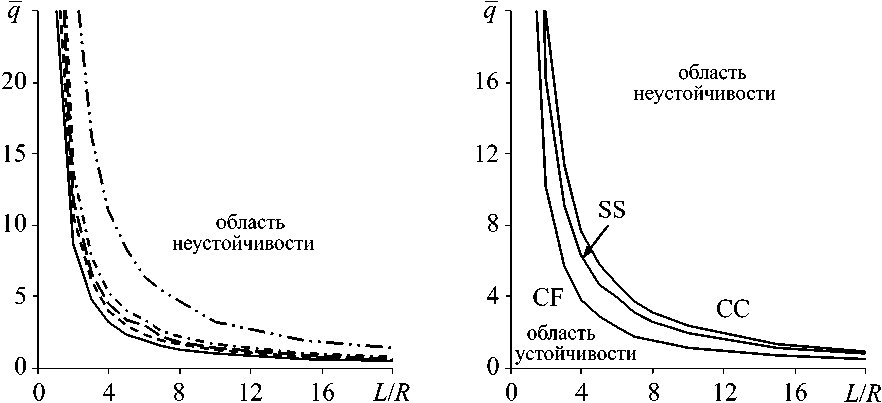
Анализ границ аэроупругой устойчивости от отношения L / R , результаты которых приведены на рис. 5, а для свободно опёртых оболочек и на рис. 5, б – для оболочек с разными граничными условиями, позволяет сделать вывод о том, что наибольшее различие в безразмерном параметре динамического давления, как в случае разных консистенцией ФГ-материала, так и в случае одной консистенции для оболочек с разными вариантами граничных условий, имеет место для оболочек средней длины.

а

б

Рис. 5. Зависимости безразмерного параметра динамического давления q от отношения

L / R для ( а ) свободно опёртой оболочки и ( б ) оболочек с разными граничными условиями при N = 1: h / R = 1000; –––– – Al; –∙–∙ – N = 1; -∙-∙-∙ – N = 2; – – – – N = 5; ----– N = 10;

–∙∙–∙∙–∙ – ZrO 2

Представленные результаты расчета позволяют заключить, что вне зависимости от варианта граничных условий, задаваемых на краях оболочек, и их линейных размеров, критические значения аэродинамической нагрузки, определяемые различными значениями показателя объемной доли, ограничены предельными величинами, вычисленными для чистых материалов. Это означает, что граница аэроупругой устойчивости ФГ-оболочек может быть откорректирована за счет изменения показателя объемной доли любого составляющего материала. Однако наиболее эффективной такая корректировка может быть только для оболочек с определенными геометрическими размерами. Кроме этого, следует иметь в виду, что предельное значение нагрузки для оболочки, состоящей из металла и керамики, будет всегда ниже, чем для изотропной оболочки, выполненной из материала с более высокой жесткостью (в данном случае керамики), тем не менее обеспечивая улучшенные эксплуатационные характеристики, в частности сопротивление температурным деформациям.

Работа выполнена при финансовой поддержке РФФИ (грант № 13-01-96049).