Исследование параметров виброполосы с помощью математической модели

Автомобилизация наряду с огромным положительным влиянием на экономику государств, создание удобства и комфорта для людей может вызвать ряд негативных явлений, человеческие жертвы, огромный материальный ущерб в результате дорожно-транспорт-ных происшествий (ДТП), шум, загазованность воздушных бассейнов городов, загромождение улиц стоящими автомобилями и, наконец, транспортные заторы и резкое снижение скорости движения. В связи с ростом автомобильного парка и интенсивности движения транспортных средств для повышения безопасности предусмотрено совершенствование мероприятий по внедрению современных способов нанесения горизонтальной дорожной разметки [1].

Проблема безопасности дорожного движения представляет собой сложный комплекс факторов, связанных с состоянием транспортных средств, дорожных конструкций, условий движения, психо-физиологического поведения водителей, плотности транспортных потоков и др. Одним из путей решения этой проблемы является создание конструктивных элементов на дорожной одежде, способствующих генерации колебаний транспортных средств в режимах некомфортного восприятия водителем условий движения. Для выбора оптимальных параметров такой конструкции необходимы математические модели, включающие в себя характеристики автотранспортных средств (АТС), скорость движения, общую длину, глубину, ширину и шаг неровности, материалы элементов конструкции шумовой полосы [2].

В организации дорожного движения нанесение горизонтальной разметки представляет важную роль. В настоящее время нанесение разметки дорог и улиц способствует снижению

Поезжаева Елена Вячеславовна, кандидат технических наук, профессор

аварийности, при этом движение транспортных средств становится более организованным и упорядоченным, улучшается информированность водителей и пешеходов. Дорожная разметка наносится в соответствии с требованиями дорожных знаков, может применяться как самостоятельно, так и с другими средствами организации движения [3]. К разметке относятся линии, надписи и иные обозначения на проезжей части, бордюрах, элементах дорожных сооружений и обстановки дорог, устанавливающие порядок дорожного движения, показывающие габариты дорожных сооружений или указывающие направление дороги.

Цель работы: построение и исследование математической модели плоских колебаний подрессорного автомобиля в режимах подпрыгивания и галопирования.

Движение АТС осуществляется в пределах так называемого «коридора рыскания». Чем выше скорость движения, тем шире «коридор рыскания», который является динамической шириной автомобиля. На динамическую ширину АТС влияют длина и угловые перемещения автомобиля, поперечные колебания кузова и прицепов автопоездов, конструкция шарнирных соединений прицепов и их количество, исправность и тип тормозного привода. Динамическая ширина существенно зависит от реакции водителя на внешние раздражители. В возникновении реакции организма, а, следовательно, на режимы управления АТС важную роль играют анализаторы центральной нервной системы – вестибулярный, зрительный, кожный и др. [4]. Закономерности и параметры движения в «коридоре рыскания» являются сложными и взаимосвязанными. Одним из вариантов аналитического подхода к решению проблемы безопасности движения в таких случаях является модель бокового заноса относительно оси движения.

Рассматриваем боковую устойчивость АТС без вращения. В этом случае необходима модель распределения коэффициентов сцепления покрытия дороги и шины АТС. Рассмотрим частный случай распределения масс, когда ρ2=a b, т.е. когда радиус инерции автомобиля равен среднему геометрическому между величинами a и b. Отметим, что для этого расстояние a + b между осями автомобиля должно быть меньше его общей длины (это на самом деле имеет место в автомобилях современной компоновки). Тогда корни частного уравнения:

работоспособности. В связи с этим необходимо оценивать практически возможные пределы повышения вибраций, снижающих уровень комфорта движения и свидетельствующих об изменении траектории движения АТС в нежелательном и опасном направлении.

Р 1 =

2 • C n ' ( a + b ) . m • b ’

Р 2 =

2 • C₃ ' ( a + b ) m • a

Для примера рассмотрим возможность применения параметров модели автомобиля ГАЗ 3221 «Газель». Технические характеристики, необходимые для расчетов, принимаем в виде: a=2800 мм, b=1900 мм m=3250 кг. Изменение жесткости передней подвески берем в пределах 10-14,4 кН/м, изменение жесткости задней подвески – в пределах 30-34,4 кН/м. Результаты расчетов представлены на рис. 1, 2. Из полученных графиков видно, что при увеличении жесткости увеличивается и частота собственных колебаний, а увеличение массы автомобиля приводит к снижению частоты собственных колебаний.

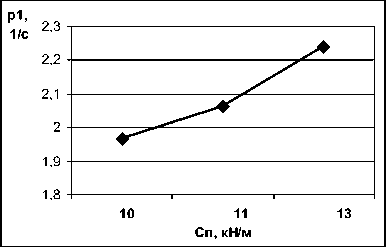
Рис. 1. Графики зависимости собственных частот колебаний кузова от жесткости

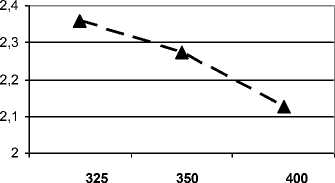
m авт, ( кг *с2/см)

Рис. 2. Графики зависимости собственных частот колебаний кузова от массы автомобиля

Рассмотрим структуру неровности вибропо-

лосы в соответствии с зависимостями: а)

V q(l) = q o • cos(2 -n-   • t),

H

б)

2 n x q = q o (1 - cos ), H

где q 0 – амплитуда отклонения поверхности от средней линии; V – скорость АТС; H – шаг неровности; х – пройденный путь; t – время прохождения неровности.

Канал вибрации включает в себя колесо, корпус, амортизаторы и водителя АТС. По модели одночастотного колебания без демпфирования амплитуда колебаний водителя запишем в форме:

Y e = q 0

p ² p 1 ² - p ²,

Выбор параметров виброполосы проводим при условии одночастотного колебания АТС. Это значительно упрощает задачу, но позволяет установить предельные значения виброскорости и виброускорения, действующие на физиологическую систему водителя с целью обеспечения адекватного управления АТС.

Повышение уровня вибрации возможно лишь до определенного предела, достижение которого связано с отрицательным влиянием на водителя, вызывая ухудшение самочувствия и снижение где р1 – собственная частота колебания АТС; р – частота воздействия.

В реальных условиях система амортизации существенно снижает амплитуду колебаний водителя. Если принять во внимание коэффициент снижения в диапазоне 50-2000, по результатам расчета виброскорости и виброускорения можно установить некомфортную зону движения (см. табл. 1).

Таблица 1. Некомфортная зона движения

Параметры, см/с	Коэффициент снижения
	50	100	150	500	1000	1500	2000
Y в	0,2	0,1	0,07	0,02	0,01	0,006	0,005
• "Y в	104	52	37	11	5	3	2,6

Перегрузку в центре тяжести АТС при движении по неровности (формула 3б) с учетом амортизации (обжатие, пневматика) без учета работы амортизатора запишем в следующем виде:

nд

м.д.

2 n V

⁶ р Y'os _и • t-

Максимальная перегрузка равна:

n д max

2^7^- [h -(sм.д. — 5пр. Я где δм.д., δпр – максимально допустимое и фактическое обжатие пневматика; g – 9,8 м/с2; h – 2q0.

Меру «неудобства» устанавливаем в пределах по октавным полосам частот при синусоидальном воздействии: 16 Гц - Y = 5 см/с; 32 Гц - Y = 3,5 см/с; 63 Гц - Y = 2,5 см/с. при этом амплитуда колебаний составляет: Y₁=0,049 см; Y 2 =0,017 см; Y 3 =0,0063 см. Время воздействия вибрации менее 10 мин.

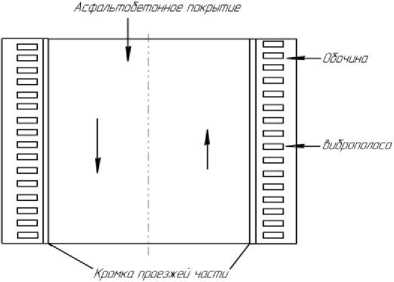
Рис. 3. Схема нанесения виброполос

Сопоставляя результаты, представленные в табл. 1, и меры дискомфорта, определяем, что коэффициент снижения амплитуд колебаний по принятой модели изменяются в пределах от 50 до 150. Это позволяет принять решение о назначении параметров виброполосы: шаг 20 см, глубина 5 см, длина полосы 1 км. Схема нанесения шумовых полос представлена на рис. 3 [5].

В дальнейшем предполагается продолжение исследований воздействия виброполосы на АТС и водителя.