Исследование первичной радиационной повреждаемости в сплаве FeCr

Метод молекулярной динамики является одним из наиболее подходящих способов моделирования каскадов атомных смещений. К настоящему времени различными группами исследователей по всему миру проведено большое количество таких исследований применительно к различным материалам. Моделирование каскадов в сплавах также широко выполняется, хотя для многокомпонентных систем сохраняется проблема подготовки надежных потенциалов.

Основной целью работы является определение ряда параметров первичной радиационной повреждаемости сплавов Fe-x%Cr с учетом процессов рекомбинации и кластеризации точечных дефектов в каскадах смещений. Моделирование проведено для нескольких сплавов с различным содержанием хрома: Fe-5ат.%Cr, Fe-10ат.%Cr и Fe-14ат.%Cr при температуре 300 К.

2. МЕЖАТОМНОЕ ВЗАИМОДЕЙСТВИЕ

где E _tot – полная потенциальная энергия сис темы, T i - тип t -го атома: Fe или Cr , p _T. - собственная электронная плотность атома T_i как функция расстояния до его центра, F _T – функция внедрения, r _ij – расстояние между атомами j и j , V _TjTj ( Г ) — парный потенциал,

V„ + V„

V FeCr = FeFe ₂ CC . h TT j ( x ) = 1 , если T i = T j , иначе h _TT ( x ) – полином Редлиха-Кистера четвертой степени,

x _ij

¹ fp Fe

2 (p ^tot

Fe

2 P j_

tot , ^p j 7

Для атомистического моделирования сплава FeCr широко применяется многочастичный потенциал межатомного взаимодействия, предложенный в работе [1], согласно которому полная потенциальная энергия системы из Ν атомов определяется как

Fe где pi - вклад в электронную плотность в узле i ( Р°‘ ) только от атомов железа.

Потенциалы для взаимодействий Fe-Fe и Cr-Cr взяты авторами [1] из работ [2] и [3] соответственно. Параметры полинома h T.T ( x ) были подобраны так, чтобы близко воспроизвести кривую энтальпии смешения случайного ферро-магнитного сплава FeCr , рассчитанную методом ab initio из работы [4].

В данной работе применен вышеупомянутый потенциал межатомного взаимодействия, но с

N                       1

Eto, = Z F t ( Z>M) + Z ^4^44 i = 1 L j * i               ² j * i

, (1)

Муралев Артем Борисович, младший научный сотрудник лаборатории Компьютерного моделирования поведения неорганических материалов Научно-исследовательского технологического института им. С. Капицы.

некоторыми изменениями, предложенными в работе [5]. Во-первых, потенциал для железа, взят из работы [6]. Во-вторых, в силу моделирования каскадов атомных смещений модифицирована репульсивная часть потенциала для взаимодействий Fe-Cr при относительно небольших (<1 Е) межатомных расстояниях. Для чего, слагаемое h _FeCr ( x ) V teC2r ( ^r ) в формуле (1) заменено следующей функцией.

V Fe _Cr (x,r) = h(x)V _F™d (r) 2 V(r) ,   (3)

где

vm:^)=*

' ^VFeCr^(r) .     r >  r 0

cr + dr , 0 < r < r0

V(r) =

z1Z 2 e e * 4л80 r

Y

Ф (-), a

a (r - r ₂ ) ³ e ^{e r} ,

0 < r < r1

r1 < r < r2

V ( r ) – экранированный кулоновский парный потенциал для r <  r 1 . Длина экранирования a определена согласно работе [7], а функция Ф ( x ) - в соответствие подходу Циглера, Берса-ка и Литтмарка [8]. Коэффициенты c , d , а и в подбираются из условия непрерывности соответствующих функций и их первых производных, r 1 = 1 Е, r ₀ и r 2 - подгоночные параметры. Подгонка проведена под энергии связи смешанных FeCr гантелей внедрений с ориентацией <110> и <111>, рассчитанных Ольссоном и др. [9] методом ab initio . Полученные значения r ₀ и r ₂ составили 2.22815 и 1.9664 Е соответственно.

3. МОДЕЛИРОВАНИЕ КАСКАДОВ АТОМНЫХ СМЕЩЕНИЙ В СПЛАВЕ FeCr

Молекулярно-динамическое моделирование первичного радиационного повреждения бинарного неупорядоченного ОЦК-сплава Fe-x%Cr проведено для пяти различных концентраций хрома x : 5, 10 и 14%.

Для моделирования каскадов атомных смещений задавались ОЦК микрокристаллиты сплава FeCr , содержащие около 10 ⁶ атомов. При этом расположение атомов разных типов в сплаве носило случайный характер, т.е. каждому атому кристаллита с вероятностью p=0.91 приписывался тип Fe и с вероятностью (1–p) – Cr . В расчётах использовались «периодические» граничные условия. Моделирование проведено при начальной температуре кристаллитов T = 300 K для энергии первично-выбитого атома (ПВА) 20 кэВ. Начальная температура обеспечивалась путем задания начальных скоростей атомам кристаллитов с последующим молекулярно-динамическим моделированием NPT-ансамбля с баростатом и термостатом Берендсена для нулевого давления и выбранной температуры в течении 30 пс с шагом по времени 1 фс . Затем, одному из атомов придавался импульс в высокоиндексном направлении <135>.

На стадии остывания каскада для каждого микрокристаллита проводился подсчет образующихся радиационных дефектов. Для этого каждому узлу i идеальной кристаллической решетки ставилась в соответствие ячейка Вигнера-Зей-ца C _i , которую можно определить как множество

всех точек пространства, расстояние от которых до узла i (с учетом периодических граничных условий) меньше или равно расстоянию до любого другого узла решетки. Обобщения подобных ячеек известны в математике и физике под названиями ячеек Дирихле и полиэдров Вороного. Отсутствие атомов в ячейке C_i трактуется как вакансия в узле i , попадание более одного атома в ячейку C _i трактуется как наличие внедрений вблизи узла i . Число дефектов определяется как общее количество ячеек Вигнера-Зейца, не содержащих ни одного атома материала.

Моделирование каскадов атомных смещений в сплаве FeCr (рис. 1) показало, что на завершающей стадии каскадов общее число «выживающих» точечных дефектов кристаллической решетки для выбранной энергии ПВА (рис. 2) практически не зависит от исходной концентрации атомов хрома в матрице. Оценка количества радиационных дефектов составила в среднем около 83 дефектов, что количественно согласуется с аналогичным результатом работы [10], в которой были исследованы каскады атомных смещений в бинарном сплаве Fe-9ат.%Cr при температуре 600 К для энергий ПВА 0.1, 0.5, 1, 2, 5, 10, 15 и 20 кэВ.

Содержание атомов хрома в междоузельных конфигурациях (рис. 3) превышает исходное содержание хрома в матрице приблизительно в 2 раза . В работе [10] оценка доли атомов Cr в междоузлиях в среднем составила « 22%, что также согласуется с аналогичным результатом для Fe-10%ат.Cr данной работы. Наблюдаемый эффект можно объяснить более высокой подвижностью атома хрома по сравнению с атомом железа в исследуемых сплавах.

Наряду с оценками числа «выживающих» дефектов, были получены оценки количества, размеров вакансионных и междоузельных кластеров (рис. 4, 5), остающихся в кристаллите после затухания каскада. Дефекты одного типа считали принадлежащими одному кластеру, если соответствующие им узлы решетки находятся на расстоянии не далее вторых ближайших соседей ( 2nn ) для вакансий и третьих ( 3nn ) ближайших соседей для междоузлий.

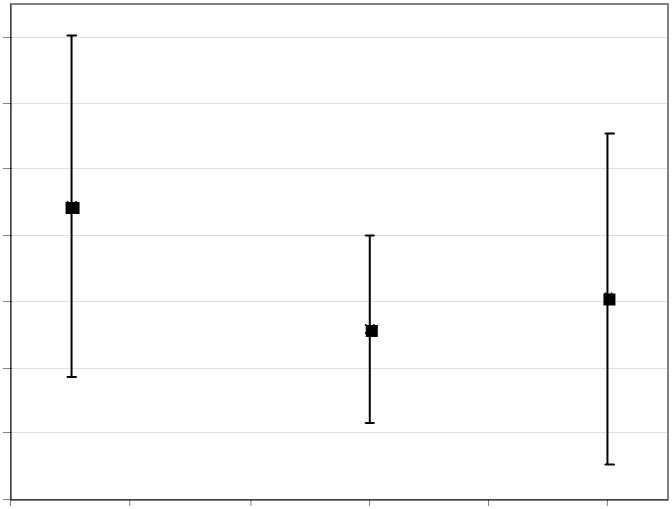
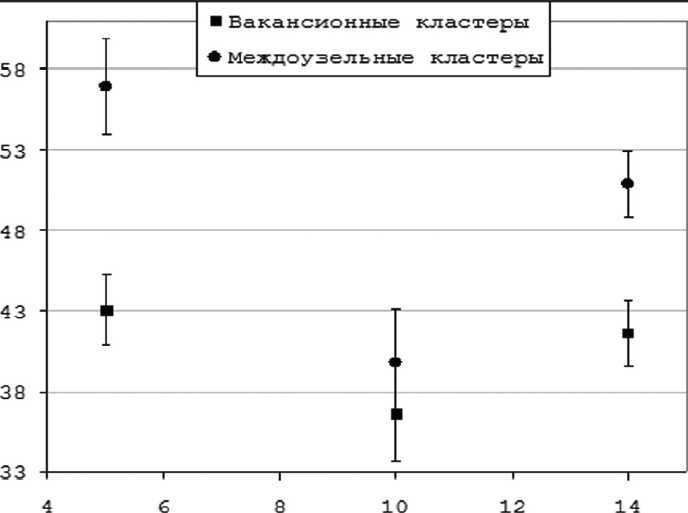
До 50% от общего числа «выживающих» радиационных дефектов на завершающей стадии каскадов связаны в кластеры (рис. 4). Для сплавов с долей атомов хрома в исходной матрице 5 и 14% кластеризуется равная с учетом погрешностей доля точечных дефектов, что несколько выше, чем для сплава Fe-10ат.%Cr. При этом, только в сплаве Fe-10ат.%Cr обнаружено практически равное количество междоузельных конфигураций и вакансий, связанных в кластеры (рис. 5); для сплавов Fe-5ат.%Cr и Fe-14ат.%Cr доля кластеризованных междоузлий выше чем

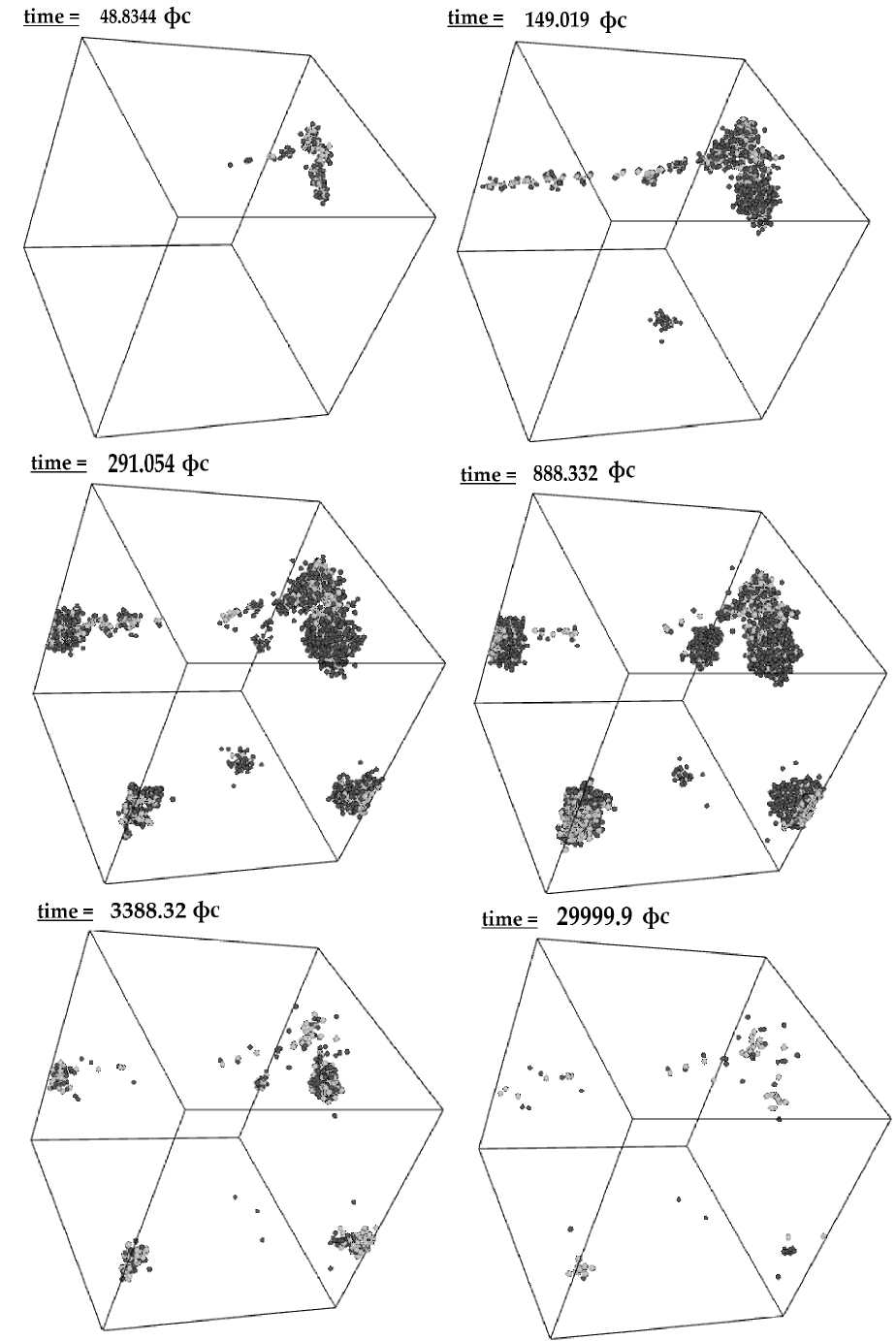
Рис. 1. Пример развития каскадов атомных смещений в бинарном сплаве Fe-10ат.%Cr (в качестве светлых окружностей выступают вакансии, темных – междоузельные конфигурации)

л <в в

а-

и

л И

о и в о ф S' к в о и

к в ф X я ф л -е

Содержание атомов Cr в матрице, %

Рис. 2. Количество образующихся пар Френкеля на завершающей стадии каскадов атомных смещений в зависимости от концентрации атомов Cr в исходной матрице

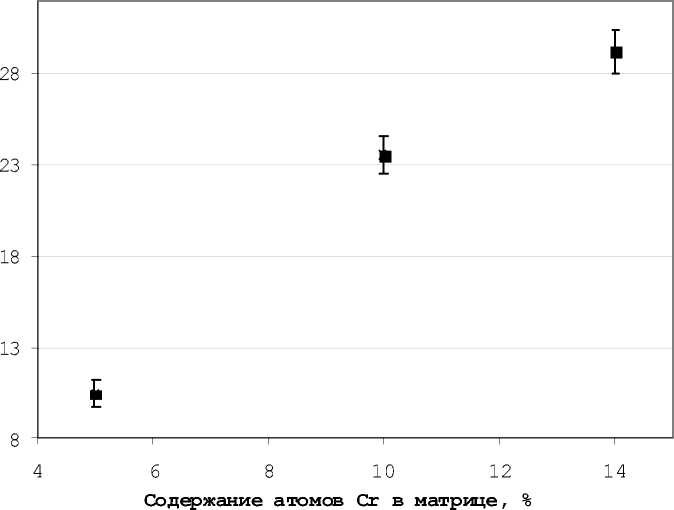
Рис. 3. Содержание атомов Cr в образующихся междоузельных конфигурациях в зависимости от концентрации атомов Cr в исходной матрице

вакансий в ≈ 1.3 раза и составляет ≈ 56 и 50% соответственно.

Средний размер кластеров “выживающих” точечных дефектов в исследуемых сплавах для выбранной энергии первично-выбитого атома, практически одинаков как для скоплений вакансий, так и междоузельных конфигураций, и составляет в среднем 3.6.

У е

У

Я о

л

Е" О 4 и К

* В о

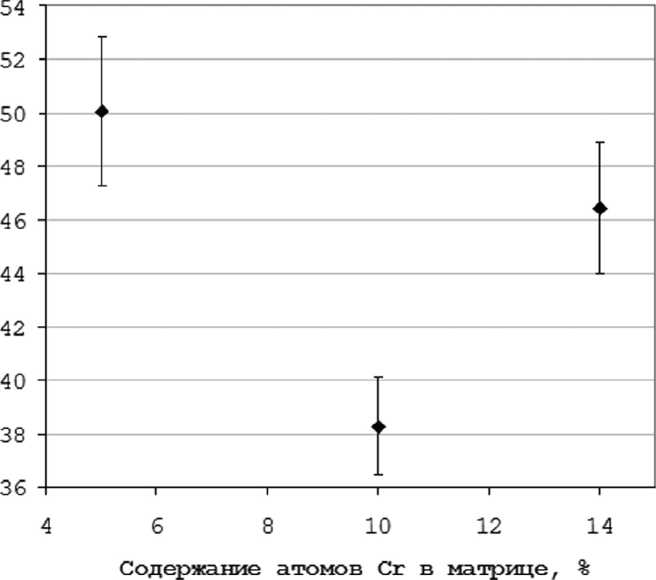
Рис. 4 . Доля точечных кластеризованных точечных дефектов в зависимости от концентрации атомов Cr в исходной матрице

v м я о ь

Содержание атомов Сг в матрице, %

Рис. 5. Доля кластеризованных вакансий и СМА в зависимости от концентрации атомов Cr в матрице

4. ЗАКЛЮЧЕНИЕ

В представленной работе путем молекулярно-динамического моделирования рассмотрены процессы первичного радиацион- ного повреждения сплавов FeCr с различным содержанием хрома в матрице: 5, 10 и 14%. Моделирование проведено при температуре 300 К для энергии первично-выбитого атома 20 кэВ. В расчетах был использован много-

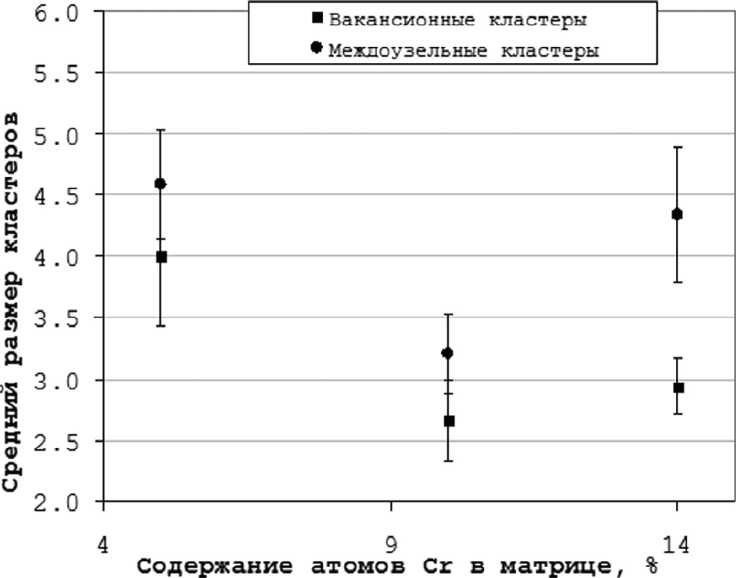
Рис. 6. Средний размер кластеров в зависимости от концентрации атомов Cr в исходной матрице

частичный потенциал межатомного взаимодействия.

Результаты проведенных расчетов позволили установить, что для выбранной энергии первично-выбитого атома, общее число радиационных дефектов, образующихся на завершающей стадии развития каскадов атомных смещений, практически не зависит от содержания хрома в исходной матрице железа. Среднее число «выживающих» точечных дефектов составляет около 83. При этом концентрация атомов хрома в междоузельных конфигурациях во всех рассмотренных кристаллитах практически в 2 раза превосходит исходную концентрацию хрома в сплаве, что количественно согласуется с аналогичным результатом для Fe-9ат.%Cr , представленным в работе [10].

Доля междоузлий, образующих кластеры, а также средний размер кластеров выше соответствующих значений для вакансионных кластеров, что можно наблюдать в похожих расчетах работ [3, 10]. При этом для одного из сплавов, а именно для Fe-10ат.%Cr , оценки доли кластеризованных дефектов в целом, а также кластеризованных вакансий и междоузельных конфигураций имеют наименьшие значения, что в свою очередь требует дальнейших проведений исследований с другим содержанием хрома в исходной матрице, а также при других значениях энергии первично-выбитого атома.

Работа выполнена при поддержке Минобрнауки в рамках государственного задания на 20122014 гг, ФЦП “Научные и научно-педагогические кадры инновационной России” на 2009 – 2013 годы и при частичной поддержке гранта РФФИ – проект 12-08-97076.