Исследование плавности движения моноблочного привода биомеханического тренажера

В каждом классе следящих систем можно выделить устройства, где плавность движения исполнительного звена является определяющим требованием. Так, например, неплавность в механизмах медленных подач биомеханического тренажера может привести к ошибке позиционирования. Высокие требования по плавности технологических перемещений предъявляются к приводам установок выращивания монокристаллов, которые обусловлены тонкостью физических процессов кристаллизации различных материалов. В металлорежущих станках неплавное движение режущего инструмента или заготовки приводит к колебаниям в относительном движении инструмента и заготовки и является причиной неточного формообразования в процессе резания, снижения чистоты обрабатываемой поверхности и повышения износа режущего инструмента. В системах автоматического сопровождения (приводы антенн радиолокаторов, тяжелых астрономических приборов, устройства перемещения кино- и телевизионных камер) требования к выходному движению определяются законом движения «цели». Здесь обеспечение плавности слежения необходимо для стабилизации повышения разрешающей способности перемещающихся приборов.

На основании анализа известных оценок плавности предложены критерии плавности, которые позволяют количественно оценивать плавность приводов с поступательным перемещением. В качестве первого показателя плавности положим отношение полной вариации скорости v ( t ) на интервале 0T - время наблюдения) к заданному значению скорости v₀ на этом интервале

, = То Varv = т„ Т 1  Tv-о    Т '

И dt v0

,

где τ 0 =H/v 0 – постоянная времени, необходимая для приведения выражения к безразмерной величине ( Н – длина штока). Второй показатель плавности определяется через полную вариацию ускорения a ( t ) = v ( t ) на интервале 0

_ т0 Var a H2 T

I2=tat=т!

M dt ^v 0 ³

.

Электромеханические приводы моноблочного исполнения на базе РВМ имеют предпосылки обеспечения выходного перемещения с высокой плавностью. Применение двигателей на постоянных магнитах серии ДБМ позволяет размещать исполнительный механизм внутри полого ротора. В такой моноблочной конструкции источник движения (двигатель) максимально приближен к исполнительному звену. Неравномерность вращения ротора будет частично сглаживаться за счет его утяжеления механической передачей. В приводе данной конструкции важную роль в обеспечении плавности выходного перемещения играет исполнительный механизм. В этом случае применение РВМ является наиболее предпочтительным [2]. Имея в сопряжении до 500 точек контакта, данные механизмы обладают высокой плавностью поступательного перемещения. РВМ компактны, имеют высокий КПД (0,85), грузоподъемность, долговечность. Большой выбор конструктивных исполнений позволяет проектировать самые разнообразные приводы на их основе. Таким образом, моноблочные электромеханические приводы на базе РВМ имеют предпосылки обеспечения выходного перемещения с высокой плавностью.

Используем двухмассовую математическую модель: первая масса (входное звено РВМ) встроена в полый ротор двигателя и вращается вместе с ним, вторая масса (выходное звено РВМ) поступательно перемещает нагрузку. В модели учитываются нелинейности люфт fЛ, «сухое трение» fТ и следующие возмущения: возмущение по напряжению ΔU, вызванное помехами датчиков обратной связи, пульсациями управляющего напряжения или момента двигателя; возмущение от кинематической погрешности ΔK, обусловленное технологическими погрешностями изготовления или деформациями звеньев РВМ при эксплуатации; возмущение от нагрузки ΔF, вызванное колебаниями нагрузки или действием внешней среды на выходное звено. Тогда:

^1

Д J рот ^ 1 = k M ( U ^{+ A} U - k X x 2 - k V v 2 - ^kv 2 ) -

SX1

<      F12-~ ^1

n PBM x 2 = v 2

m ₂ v ₂ = F 12 + A F - k P x ₂ — k S v ₂ —

- f_T ( v 2 , F 12 - k p X 2 — k_sv 2 ) , где

^F 12 = c ^f Л ^{( S}x T 1 - x 2 ^{+ A} к ^{) +}

+ bf Л (SX^1 - x2 + AК )

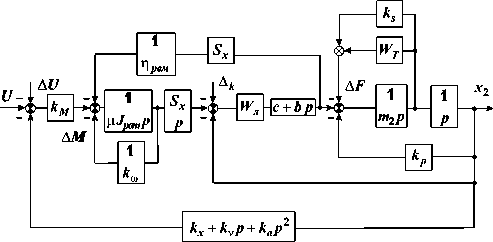
Рис. 1. Структурная схема привода

Системе уравнений (3) соответствует структурная схема рис. 1. Передаточные функции для каждого возмущения имеют вид: - передаточная функция по напряжению:

W u ( p ) =

x 2 ⁽ p ) ₌ q _n ^kM и ( p )   Sk + k „ k x

T b P + 1           .

Ap ⁴ + Bp ³ + Cp² + Dp + E ’

- передаточная функция по возмущению от кинематической погрешности:

xkdpl-„    ^tq p Tp ^{+ 1 ) ( T}» p ⁺ 1)  .

W A ^{( p} ) =        = ^qЛ .4      3      2            ;

A/r(p)    Ap + Bp + Cp + Dp + E

- передаточная функция по возмущению от нагрузки:

_w ( \₌ x 2 ( p ) ₌ S n ^{+ k}M^ka m 2 ^T 12 p (T ^ p ^{+ 1 )+} Чя ^ ⁺ 0 ^fVp)  A F ( p)  S^kp + k_Mk_x  Ap ⁴ + Bp ³ + Cp ² + Dp + E ■

Показатели плавности при гармонических возмущениях имеют вид:

1 1 = 2

П

I i Ю kWk (i ^ k )|v0

to kH

v0

,

_ 2 V ^Ю k^Wk ^Ю k ⁾

I 2 =

n      v0

to k H

I   v 0   J

,

где k - номер возмущения, Wk - передаточная функция k-го возмущения. По формулам (7) определено влияние параметров системы на плавность привода при действии гармонических возмущений. Одной из причин неплавности движения является зазор в передаче. В следящем приводе зазоры уменьшают точность слежения, могут являться источником неплавности движения и автоколебаний (АК). При исследовании динамики люфт моделируется «зоной нечувствительности». Гармоническая линеаризация позволяет получить аналитические условия возникновения АК и определить частоту и амплитуду АК. Например, при kP = kS = b = 0 to А = 1/ JTq (Tm  8 T ,I

q л (A АК ) = T2 /8 Tq TM -8 T J •

Условие автоколебаний в этом случае примет вид:

8 T q ( T M -8T . ) - T 2² >  0 .

Численное решение не линеаризованной системы (3) показало, что в следящей системе с люфтом (при b =0) возникают пилообразные АК. Так, амплитуда АК зависит от А Л и b , а частота АК уменьшается с ростом ^, m 2 , k a , k_m и с уменьшением k_X и k_V . Плавность выходного перемещения при наличии АК определяется их частотой и амплитудой: I 1 ~ A ak M ak , 1 2 ~ A ak №² ak •

При исследовании плавности работы привода необходимо рассмотреть режимы работы на низких скоростях, где неплавность движения может быть значительной [3]. Неплавное движение на низких скоростях связано с фрикционными автоколебаниями (ФА), возникающими в приводе. Проведем анализ динамики разомкнутого по положению привода с «сухим трением» на выходном звене. Принимаем экспоненциальную модель кинетической характеристики трения: F T ( v ) = F A - ( F A - F B ) exp ( - v_T/v ) • После линеаризации F^v ) и при допущении малости колебаний (колебания нагрузки не отражаются на вращении ведущего звена) аналитически получено условие возникновения ФА:

FA - F_r v_T       v_T 1  ,

—---B-—exp - — I > b v 0    v 0 I v0)    ,               (11)

позволяющее определить критическую скорость v _кр возникновения ФА. Частота ФА линеаризованной системы определяется как

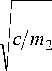
b - ( F A

При численном исследовании не линеаризованной системы были выявлены следующие качественно различные режимы (рис. 2). При v ₀> v _кр автоколебаний в системе нет и выходное звено движется с постоянной скоростью v ₀. Если v_рел < v ₀< v _кр (—), то в системе устанавливаются гармонические ФА (без остановок). Начиная с некоторого значения скорости скольжения v ₀~ v _рел (—), колебания становятся релаксационными (с остановками). При дальнейшем уменьшении v _0< v _рел растет время стоянки выходного звена за цикл.

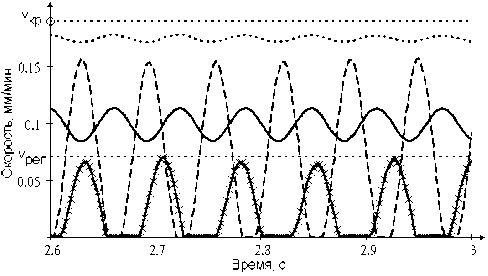
Рис. 2. Автоколебательные режимы в системе

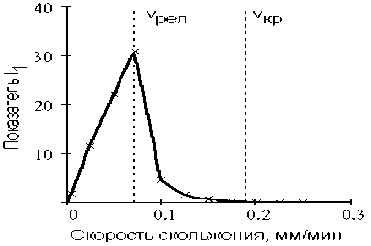
Проведем численный анализ плавности выходного перемещения при наличии ФА в зависимости от параметров привода. На рис. 3 в качестве примера представлена зависимость плавности от скорости скольжения. Показатели имеют максимум при переходе от релаксационных ФА к гармоническим, т.к. при v ₀= v _рел амплитуда ФА максимальна. При изменении параметров в области гармонических колебаний показатели убывают при уменьшении скачка силы трения, увеличении КПФ, скорости скольжения, массы нагрузки, жесткости и демпфирования [3].

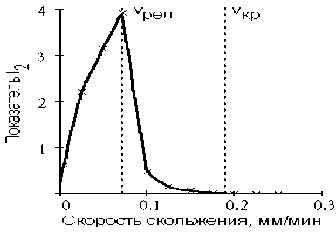
Рис. 3. Зависимость показателей плавности от скорости скольжения

Для проверки адекватности математической модели проведено экспериментальное определение динамических характеристик моноблочного электромеханического привода. В качестве экспериментального образца выбран моноблочный привод системы управления стабилизатором. В ходе измерений определялись АФЧХ замкнутого по положению привода при подаче постоянного и синусоидального управляющего сигнала с позиционной нагрузкой k _p=100 H/мм и без нагрузки. Расхождение между опытными и теоретическими АФЧХ не превышало 0,4 мм (без нагрузки) и 0,9 мм (с нагрузкой) для АЧХ и 5 (без нагрузки) и 7 (с нагрузкой) для ФЧХ, что лежит в пределах ошибки измерений (рис. 4).

Самыми трудно устранимыми причинами неплавности поступательного перемещения роликовинтовых механизмов являются кинематическая погрешность и зазоры. Для оценки плавности РВМ путем моделирования кинематической погрешности выявлено, что высокочастотные составляющие периодических погрешностей элементов РВМ существенно влияют на плавность механизма. Для определения зависимости плавности от того или иного геометрического параметра роликовинтового механизма реализации кинематической погрешности, полученные при различных значениях параметра, обрабатывались критериями плавности.

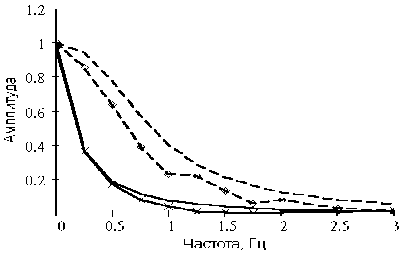
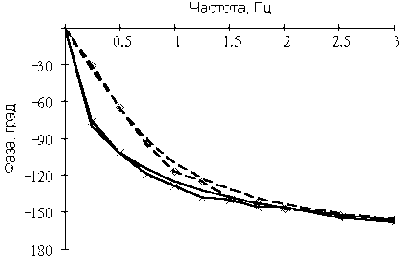
Рис. 4. Сравнение теоретических и экспериментальных АФЧХ привода без нагрузки:

▬▬ теоретическая; ▬×▬× экспериментальная; с нагрузкой: ▬ ▬ теоретическая; ▬ ◊ ▬ экспериментальная

Поскольку зазоры в исполнительном механизме значительно ухудшают плавность приводов, при проектировании механической части привода с высокой плавностью выходного перемещения следует правильно оценивать зазоры или выбирать пути их устранения.

Проведены расчеты максимального осевого зазора в зависимости от вида сопряжения и класса точности изготовления. Так, величина осевого зазора РВМ растет с увеличением осевого шага, межосевого расстояния, класса точности и перехода вида сопряжения от H к D . При больших значениях геометрических размеров звеньев РВМ, осевом шаге Р Х ≥2 мм и классе точности k T ≥4 величина осевого зазора может принимать значения 0,2-0,5 мм.

Выборку зазоров в роликовинтовых механизмах можно осуществить двумя способами. В первой группе выборка зазора осуществляется осевым смещением разрезного резьбового элемента (винта, ролика, гайки), во второй – дополнительным поворотом одного из резьбовых элементов. Для определения эффективности мероприятий по выборке люфта с помощью РВМ с разрезными звеньями и выработки рекомендаций по их проектированию проведен анализ динамики таких устройств в составе привода. Это позволило разработать методику расчета жесткости устройств выборки зазора в РВМ, при которой автоколебания, вызванные зазором, отсутствуют. При синтезе системы учитываются ограничения на такие характеристики системы, как мощность, качество переходного процесса, быстродействие, масса и габариты привода и т.п. при оптимизации по критерию плавности.

Синтез моноблочного электромеханического привода с высокой плавностью выходного перемещения проводится в несколько этапов: силовой синтез исходя из предельных динамических возможностей привода и определение КПФ по минимуму потребляемой мощности; синтез параметров системы по качеству переходного процесса; проектирование исполнительного механизма привода с высокой плавностью выходного перемещения; проведение проверочных расчетов, определение динамических характеристик и показателей плавности спроектированного привода. Силовой синтез модуля по минимуму потребляемой энергии предполагает решение следующих задач: расчет требуемой мощности и приемистости двигателя, выбор его типономина-ла; определение необходимости форсирования, его длительности и тепловой режим; расчет граничных значений допустимого диапазона передаточных функций механизма; расчет оптимального значения КПФ по минимуму потребляемой мощности, определение оптимальной рабочей точки. Методика силового синтеза базируется на анализе предельных динамических возможностей и разработана с учетом конструктивных особенностей РВМ, а также теплоэнергетических преобразований в двигателях серии ДБМ.

Синтез параметров системы по качеству переходного процесса позволяет обеспечить максимальную плавность в системе при сохранении требуемой точности. Существует ряд систем, для которых переходный режим является основным режимом работы. В работе получены аналитические выражения показателей плавности для оценки переходного процесса и показано, что необходимым условием плавного и вместе с тем точного движения (I0→min) является переходный процесс без перерегулирования (ζ1=1). Из этого условия

M 0 =

( 1 + k _m S X S n ( k s + q_T ) + k M k v ] У

⁴ S X k m J рот ( S n k P ⁺ k M k x )

.

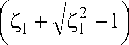
-Y

, Zi> 1;

A = 2 T J

1      ^T 1

e — 1 ,

Y e

e ⁿ- 1

Z 1 = 1;

Z 1 < 1

Выводы: при проектировании РВМ с высокой плавностью важное значение имеет выбор ведущего звена исполнительного механизма, влияющий на суммарную массу привода. Показано, что при M 0 <3-4 следует применять схему с ведущим винтом, при M 0 >3-4 – с ведущей гайкой. Применение данной методики позволило спроектировать привод системы управления стабилизатором, у которого показатель I ₁ снижен на 16%, а показатель I 2 – на 73% по сравнению с обычной методикой.

I 2 =

T

T 1

/        I -------\-2 Y

1 + 2 ^Z 1 +Vz 2 - 1 )

^1 + 2 e

-2

,

Y n-arctg

2zJ1-z2

\

1+2

e

к

2z 2

-1

e nY

-

Z 1 >  1;

Z 1 = 1;

, Z1 < 1

Из этого условия можно определить оптимальное значение суммарной массы привода