Исследование плазмон-поляритонного резонанса методом трансфер-матриц

Интенсивное развитие современных технологий сопровождается большим количеством экспериментальных и теоретических исследований поверхностных плазмон-поляритонов и их использованием в различных устройствах [1-3].

Так, например, “микроскоп на поверхностных плазмонах” имеет и на сегодняшний день широкий спектр применимости в различных сферах наук: физики, химии, биологии и др. На практике было проверено и установлено, что этот микроскоп может служить сенсором, способным быстро и надежно детектировать наличие тех или иных химических веществ в исследуемой среде благодаря своей высокой разрешающей способности и чувствительности [4]. Кроме того, плазмоны можно рассматривать как средство передачи информации в компьютерных чипах [5]. Разработке новых конфигураций устройств на основе плазмонного резонанса посвящены статьи [6-8].

Целью работы является исследование особенностей прохождения света в слоистых наноструктурах и расчет коэффициента отражения. В настоящей работе были решены следующие задачи:

• 1)    построить трансфер-матрицы для описания прохождения света в 3-слойной и 4-слойной наноструктурах;

• 2)    применить построенные матрицы для расчета коэффициента отражения в структурах воз-дух-золото-стекло и воздух-протеиновая плен-ка-золото-стекло.

2.УСЛОВИЕ СУЩЕСТВОВАНИЯ ПОВЕРХНОСТНЫХ ПЛАЗМОНОВ

Новизна исследования: проведен расчет электромагнитного отклика золотой нанопленки методом трансфер-матриц с использованием веще-

ственной диэлектрической проницаемости золота, взятой из теории Друде-Зоммерфельда. В рамках этого формализма найдена зависимость коэффициента отражения от частоты падающего излучения и толщины пленки в слоистых структурах: стекло-золотая нанопленка-воздух и воз-дух-протеины-золотая нанопленка-стекло.

Рассмотрим задачу о прохождении электромагнитной волны через границу двух сред: 1-металл, с характеристиками Е 1 и ^ 1 , 2- диэлектрик, с характеристиками Е ₂ и д ₂ .

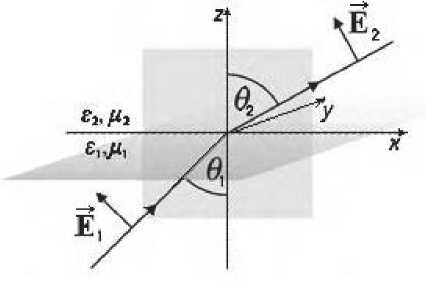
Рис. 1. Прохождение электромагнитной волны через границу раздела двух сред металл-диэлектрик

При прохождении границы раздела сред электромагнитная волна описывается решением однородного уравнения Максвелла:

• - to2         -

• VxVxE(r,to)- 2"e(r,to)E(r,to) = 0. (1) c2
3.ПОВЕРХНОСТНЫЕ ПЛАЗМОНЫ В СЛОИСТЫХ СТРУКТУРАХ

Обозначим E 1 , E 2 — напряженность электрического поля в 1 и во 2 среде соответственно.

Решение можно представить в виде [2]:

E

——

E - j

E

e ik x x ^-^    z , j - 1,2,

„               „          2тг k2 + k2 - e k2, k - — x      j, z      j , x

•

Рассмотрим образование поверхностных плазмон-поляритонов при прохождении электромагнитной волны через слоистую структуру (рис. 2).

Так как поля электрической индукции в обоих полупространствах не имеют источников, т.е. у. D _- о , приходим к равенству:

kE ■ k E _z- 0, j - 1,2. x ^j , x        ^j , ^{z j} , ^z

Теперь с учетом и решение можно записать в форме:

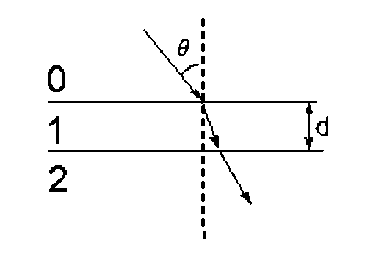
Рис. 2. Прохождение электромагнитной волны через слоистую структуру: 0(воздух)– 1(золотая нанопленка)–2(стекло)

——

E =E

I           I , x

- k x

k

e ^j , j - 1,2.

Волна поляризована в плоскости падения и удовлетворяет граничному условию:

^Eix - ^E 2, x - 0 e 1^E1z - e , E 2, z - 0. (5)

Уравнения и образуют однородную систему. Условием существования решения такой системы является дисперсионное уравнение [2]:

e , k ₂ , _z - e ₂ k ,, _z - 0.             (6)

Из в сочетании с и получаем дисперсионное соотношение:

Волна в каждом слое щими выражениями [2]:

описывается следую-

A

—

E 0

= F ⁺

E 0

- k x

V ^k 0, z

e ik ⁰z ^z

F ^-

E 0

e ^lk0z ^z ,

!?-

V ^k 0 z 2

( A k2-.-.k2-_es_£;, K-® ex + e2     e + e2 c2        c

e^-(7)

—

E 1 - E 1 ⁺

ik z e ^{l> z}

e;

e

- ik iz ( z - d )

Мы хотим найти распространяющиеся волны. Это значит, что компонента волнового вектора вдоль границы раздела должна быть действительной. С другой стороны, мы хотим найти локализованные вблизи поверхности раздела волны. Для этого нормальные к поверхности компоненты должны быть чисто мнимые. В этом случае будет наблюдаться экспоненциальное спадание полей при удалении от границы. Из и получаем условия существования локализованных поверхностных плазмонов:

e 1 ( to ) • e ₂ ( to ) <  0, e 1 ( to ) + e ₂ ( to ) <  0.

Следовательно, одна из диэлектрических функций должна быть отрицательной и по абсолютной величине превосходить другую [1, 2].

V k 1. z 2

V k ^, z 2

—

E ₂ - E ₂ ⁺

ik 2, z ⁽ z ^- d ) e .

^{- k}x

V ^k 2- z 2

Здесь E ,+ — амплитуда падающей волны, E 0" — амплитуда отраженной от границы раздела воздух/золото волны, E ; — амплитуда прошед-

шей в золото волны, E" — амплитуда отраженной от границы раздела золото/стекло волны, E + — амплитуда прошедшей в стекло волны.

В случае золотой пленки существенная дисперсия имеет место только для Е ^ = Е ^ ( to ), в то время как Е ₀ и Е ₂ (для диэлектриков) можно рассматривать как не зависящие от частоты положительные величины [6].

Будем предполагать, что металл (золото) описывается _{2 2} моделью Друде: Е 1 ( to ) = 1 — to pi / to , где to pi — частота колебаний электронной плазмы в золоте, а to — частота падающего излучения.

Запишем дисперсионные соотношения для каждой границы раздела сред. Для границы воздух / золото:

to     Е02       ,   _ toЕ^

*                 , k 1 z4 I .

С E ₀ + E₁      • С    E ₁ + E ₀

Обозначим: К0 = k0 z / k1 z, ^0 = E1 / E0. Для границы золото/стекло:

,    to   E ,    to   еЕ К, к =— —1— ,k. =— —2— ,к = -22^ ,n=

1,z                        2,z                        11

С  Ei + Е2        С ' Ei + Е2 k2 z

Используя условие непрерывности векторов

D и E на границе раздела, можно записать в матричном виде:

' E о+ J = £ Г1 + к^ 1 — к^ Y1   0 Y E i+ tE0 J 2 (1 — ед 1 + К1Л1 Д0 ek 1,zZ JtE 1_ г E1J = Г e—ik'zz 0 J 1Г1 + к 2^ 2 1 — к 2^ 2 ^Г E 2 vE1— J ( 0     1J 2 11 — к2^2 1 + К2^2 J(E0

Эти уравнения запишем в трансфер-матрич-ном подходе [2]:

В пакете Mathematica была получена и исследована зависимость коэффициента отражения от частоты падающего излучения. На рис. 3 показан 3D-график: по оси OZ отложен коэффициент R, по OY — толщина пленки d, по OX — частота падающей волны.

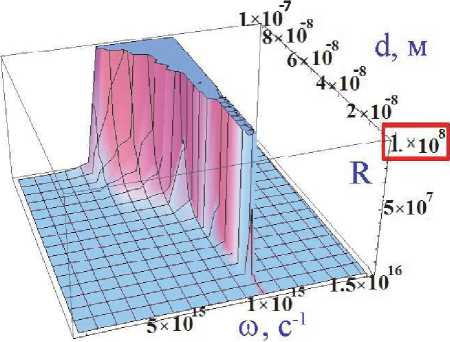
Рис. 3 . 3D-график зависимости коэффициента отражения от частоты падающей волны и толщины золотой пленки при проникновении волны из золота в стекло

Вывод: Как видно, в диапазоне волн 10 ¹⁵ — 5 •Ю ¹⁵ Гц золотая пленка становится прозрачной. Это т.н. скин-эффект. Толщина пленки оказалась меньше величины скин-слоя (для золота скин-слой в рассматриваемых условиях равен 100 нм). На частотах, близких к to _pl = 1.371 ^ 10 Гц, коэффициент отражения резко возрастает. Образование поверхностных плазмонных волн существенно зависит не только от частоты падающего света, но и от толщины слоя металла, расположенного между диэлектриками.

E ⁺ )

E ₀

E

—

- T Ф T

¹ 0,1 ^ 1 ¹ 1,2

E 2 ⁺ j

0 J

T

0 1

2 ( 1 — КЩ 1

^{1 — К} 1 П 1 j

1 + К 1 Л 1 J’

^ф 1

T =

¹ 1,2

e

t

U t 1 _Z z • d

0 j

ik z •d e 1 z   J

1 Г ^{1 + К} 2 ^ 2 2 t ^{1 — К} 2 ^ 2

^{1 — К} 2 ^ 2 '

^{1 + К} 2 ^ 2 J

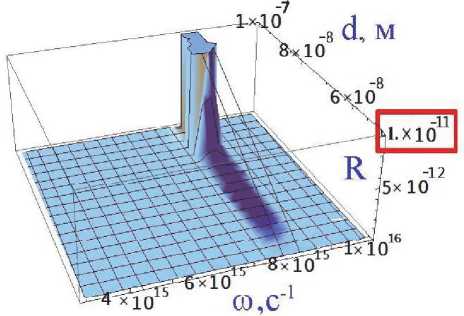
Рис. 4. Трехмерный график зависимости коэффициента отражения от частоты падающей волны и толщины золотой пленки, при добавлении слоя протеинов на золотую пленку

Коэффициент отражения определяется фор-

мулой: R( to , k x ) =

\EvL

I E 0⁺ \²"

В рамках формализма трансфер-матриц в работе решена еще одна задача, аналогичная первой, но с добавлением между воздухом и золотой пленкой слоя протеинов (d=5нм).

Вывод: При добавлении на золото слоя протеинов коэффициент отражения уменьшился на несколько порядков. Это видно из сравнения рис. 3 и 4. Т.о., слоистая структура оказалась очень чувствительной к добавлению даже одного тонкого слоя протеинов. Этот факт дает возможность использовать данную конструкцию в качестве биосенсора.

• 4.    ЗАКЛЮЧЕНИЕ

В данной работе рассмотрено возникновение плазмон-поляритонного резонанса в слоистых наноструктурах.

• 1.    В рамках метода трансфер-матрицы построена математическая модель плазмонного резонанса в структуре диэлектрик-металл-диэлектрик.

• 2.    Найдена зависимость коэффициента отражения от частоты падающего излучения в слоистой структуре: стекло-золотая нанопленка-воздух. Показано, что образование поверхностных плазмонных волн существенно зависит не только от частоты падающего света, но и от толщины слоя металла, расположенного между диэлектриками.

• 3.    Найдена зависимость коэффициента отражения от частоты падающего излучения и толщины золотой нанопленки в слоистой структу-

• ре: воздух-протеины-золотая нанопленка-стекло. Показана сильная зависимость плазмонного резонанса от состава слоистой структуры.

Эти результаты позволяют применить метод трансфер матриц к описанию поверхностных плазмонных волн, возникающих в современных наноструктурных материалах. Полученные результаты соответствуют результатам других теоретических исследований, опубликованных в открытой печати.