Исследование подходов к многоагентному моделированию систем защиты информации

DOI:

В связи с быстрым развитием информационных технологий защита информации подразумевает под собой контроль множества компонентов защищаемых систем, однако существующие системы не могут в полной мере обеспечить данный контроль из-за того, что имеют централизованную структуру, характеризуются неразвитыми адаптационными возможностями, пассивными механизмами обнаружения атак, значительной деградацией трафика целевых информационных потоков из-за большого объема ресурсов, выделяемых на защиту [6; 8].

Перспективным подходом к построению комплексных систем защиты информации является использование интеллектуальных многоагентных систем [4].

В отличие от классического способа, когда проводится поиск некоторого четко определенного (детерминированного) алгоритма, позволяющего найти наилучшее решение проблемы, в мультиагентных технологиях решение получается в результате взаимодействия множества самостоятельных целенаправленных программных модулей, так называемых интеллектуальных агентов [1; 5; 7].

Агент – это программно или аппаратно реализованная система, обладающая следующими свойствами:

– автономность – способность функционировать без прямого вмешательства людей или компьютерных средств и при этом осуществлять самоконтроль над своими действиями и внутренними состояниями;

– общественное поведение, то есть способность взаимодействия с другими агентами (а возможно, людьми), обмениваясь сообщениями с помощью языков коммуникации;

– реактивность – способность воспринимать состояние среды (физического мира, пользователя) через пользовательский интерфейс, совокупности других агентов, сети Internet или сразу всех этих компонентов внешней среды;

– целенаправленная активность – способность агентов не просто реагировать на стимулы, поступающие из среды, но и осуществлять целенаправленное поведение, проявляя инициативу.

В процессе функционирования многоагентной системы защиты должны решаться следующие задачи:

– взаимодействие агентов – установление динамических отношений между агентами;

– организация агентов – механизм разрешения или запрещения взаимодействий между агентами;

– принятие агентами общего решения.

Для систем защиты информации механизм принятия решений является одним из наиболее критичных, так как непринятие своевременных мер может привести к нарушению защищенности отдельного узла или всей информационной системы в целом [2; 3].

В общем виде проблема принятия решений группой агентов определяется следующим образом:

Пусть A = { а } - множество агентов. Общее для всех них множество стратегий X A = { x : A ^ X } (множество отображений А ) -множество стратегий многоагентной системы А , состоящей из агентов a е A .

Пусть для к е X и а е A определено ж : а ^ к - постоянные отображения A в X, принимающие для всех а е A одно и то же значение к е X . Их подмножество А = { (ж ^к ) _{к е} x } с X A образует диагональ X^A .

Таким образом, проблема принятия решений формулируется следующим образом: систему, находящуюся в некотором состоянии о е X A , привести в некоторое состояние о ^к е А, то есть агентов, находящихся в различных состояниях, привести в одно и то же состояние к е X .

Основными тремя подходами к принятию решения множеством агентов являются:

– некооперативные игры;

– кооперативные игры;

– социальный выбор.

В некооперативных играх каждый агент осуществляет выбор действия x_i , принадлежащего допустимому множеству X, , i е N = { 1,2,..., n } - множеству агентов. Выбор агентами действий осуществляется однократно, одновременно и независимо.

Выигрыш i-го агента зависит от его собственного действия x е X, и от вектора действий xx—o=(x(1x xi(2),... xi(-1), xi(+1),..., xi(n))е

X v ( - ) =niO • е N{i}) = X , j• .

оппонентов N /{ i } , и от состояния среды и ей , и описывается действительно-значной функ цией выигрыша f₁ = f ( и, x ) , где x = ( x i , x -i ) = ( x 1 , x 2 , ..., x n ) е X = ^П еN X j .

Для принятия решений этими агентами составляется таблица, называемая платежной матрицей. Каждая измерение матрицы – это игрок, первое измерение определяет стратегии первого игрока, а второе – второго и т. д. На пересечении стратегий определены выигрыши, которые получат игроки.

В силу гипотезы рационального поведения каждый агент будет стремиться выбрать наилучшие для него действия при заданной обстановке. Обстановкой для него будет совокупность состояния среды и ей и обстановки игры x ( i >=(x(1), x(2), - X(i—1), X(i+1),..., x( n)) е

X (— i ) =Ц( /• е N /{ i }) = Xj• .

Следовательно, принцип принятия им решения о выбираемом действии можно записать следующим образом:

k ( x ,) = max, „, f (и, x ,., x ), i е N . i x — i / x ^ е x ^ j i x ⁷ i⁷ — i /⁷

Это значит, что стратегия x для игрока a строго доминирует над стратегией x ', если результат стратегии x лучше для игрока a , чем результат стратегии x ', при любом выборе стратегий другими игроками, то есть стратегия, принимаемая агентом, – стратегия, которая максимизирует прибыль данного агента при любых действиях оставшихся агентов. Для того чтобы адекватно принимать решения, необходимо, чтобы каждый агент знал всю информацию о других агентах: обозреваемое состояние среды, если обозревание частичное, механизм принятия решений и возможные варианты решений.

В данной стратегии возможен случай, когда реализация доминантных стратегий агентов приносит прибыль каждому агенту или их группе намного меньше, чем при реализации недоминантных стратегий («дилемма заключенного»). Этот недостаток можно устранить путем добавления возможности общения между агентами, и такая игра называется кооперативной.

Кооперативная игра задается множеством игроков N = {1,..., n} и характеристической фун кцией v: 2N ^ R, ставящей в соответствие каждой коалиции игроков S с N ее выигрыш.

Дележом игры ( N , v ) называется вектор x = ( x ₁, ..., x_n ), для которого выполняется свойство эффективности (свойство индивидуальной рациональности) x_i >  v ({ i }) , i е N .

Решением кооперативной игры обычно считается множество дележей, которые реализуемы при рациональном поведении игроков. Различные концепции решения кооперативных игр отличаются предположениями о рациональном поведении игроков.

Говорят, что дележ x доминирует над дележом по коалиции S ( x ф , у ) , если V i е Sx _i > y, , ^ _{i е} Sx,< v ( S ) . Если существует такая коалиция S , что x ф S y , говорят, что дележ x доминирует над дележом y .

Данная игра отличается от некооперативной возможностью передавать и запрашивать данные о действиях других агентов, что позволяет точно определить доминантную стратегию, реализуемую каждым агентом.

Принятие решений на основе социального выбора заключается в том, что каждый агент взаимодействия отмечает приоритетный для него набор стратегий в некотором наборе предпочтений L . Этот набор представляется для некоторого агента a_i е A в виде последовательности элементов a_i : x ₁ >  x ₂ >  x ₃.

Таким образом, для данного агента a_i стратегия x ₁ предпочтительнее стратегии x ₂ и x ₃, а стратегия x ₂ предпочтительнее x ₃.

Множество агентов, которые предпочитают стратегию x_i стратегии x_j , обозначается как # ( x ^ i ф x ^ j ) .

Наиболее предпочтительная стратегия x е X является выигрышной по условию Кондорсе. Стратегия удовлетворяет условию Кондорсе, если V x'е X ,# ( x ф x ') > # ( x 'ф x ) . Данное условие выбирает стратегию x , определенную большинством агентов.

Однако для некоторых наборов предпочтений L не существует победителя по условию Кондорсе. Таким образом, последнее не всегда указывает конкретный вариант выбора.

Альтернативой может являться условие, основанное на идее условия Кондорсе, такое как набор Смита. Набор Смита – наименьший набор S с X , имеющий свойство V x' е S , # ( x ф x ') ># ( x ' ф x ) .

Основной класс голосований – неранжированные голосования. В данных голосованиях каждый агент отдает свой голос за одну стратегию. Примером является голосование множества.

Голосование множества. Здесь каждый агент a ∈ A отдает свой единственный голос за стратегию. Стратегия, получившая большинство голосов, побеждает в голосовании.

Однако данный класс голосований обладает весьма ограниченной способностью выражения предпочтений агентов. Класс голосований, который устраняет данный недостаток, называется ранжированным голосованием.

Самым известным ранжированным голосованием является множество с устранением.

Множество с устранением. Каждый агент a ∈ A имеет один голос и отдает его за наиболее предпочтительную стратегию. Стратегия с наименьшим количеством голосов удаляется из голосования, а агенты, которые за нее голосовали, голосуют заново за одну из оставшихся стратегий. Этот процесс повторяется, пока не останется одна стратегия, которая и считается победителем.

Голосование Борда. Каждый агент a ∈ A предоставляет полный набор предпочтений L . На основании этого набора каждой стратегии начисляются очки.

Так, если существует набор предпочтений L из n стратегий, то самой предпочтительной из них начисляется n – 1 очко, второй – n – 2 очка и т. д. Последнему предпочтению не начисляется очков вообще. Победителем считается стратегия, набравшая в сумме наибольшее число очков от всех агентов.

Голосование Ненсона. Метод Ненсона – разновидность голосования Борда, который устраняет из голосования стратегии с наименьшим числом очков, повторяет голосова- ние и опять устраняет слабые стратегии. Данная последовательность будет продолжаться до тех пор, пока не останется одна стратегия, которая будет считаться победителем.

Особенность метода Ненсона заключается в том, что он всегда возвращает стратегию из множества победителей Кондорсе, если оно не пусто, иначе возвращается стратегия из множества Смита.

Сравнение характеристик рассмотренных подходов к принятию решений приведено в таблице.

Таким образом, наилучшим подходом к принятию решений является социальный выбор. Каждый из представленных выше методов социального выбора может неадекватно выбирать стратегию из-за особенностей алгоритма выбора.

Для оценки выделенных методов социального выбора была разработана программа, на которой были проведены экспериментальные исследования.

Эксперимент 1. Пусть имеется многоагентная система, состоящая из 1 000 агентов. Предпочтения агентов имеют следующий вид:

– 499 агентов выбрали предпочтения a >  b >  c ;

• –    3 агента выбрали предпочтения b >  c >  a ;

  – 498 агентов выбрали предпочтения c >  b >  a .

В данном случае оптимальной стратегией является стратегия b , несмотря на то что ее как высокоприоритетную выбрало наименьшее число агентов. Причина этого в том, что стратегии a и c выбрали в качестве неблагоприятных 498 и 499 агентов соответственно.

Метод голосования множества должен присвоить стратегиям a , b , c баллы 499, 3, 498 соответственно и выбрать стратегию a .

Метод голосования множества с устранением на первом этапе присваивает страте-

Сравнение протоколов

Показатель	Некооперативные игры	Кооперативные игры	Социальный выбор
Принятие решений	Каждым агентом отдельно	Каждым агентом отдельно	Выбор общей стратегии, устраивающей большинство
Жесткий контроль действий агентов	Отсутствует	Отсутствует	Присутствует
Использование данных о выборе агентов для обучения	Отсутствует	Отсутствует	Присутствует

гиям a , b , c баллы 499, 3, 498 соответственно и удаляет стратегию b из набора. На втором этапе стратегиям a и c присваиваются баллы 499 и 501 соответственно и устраняется стратегия a . Остается только стратегия c .

Метод Борда должен присвоить стратегиям a , b , c баллы 998, 1003, 999 соответственно и выбрать стратегию b .

Метод Ненсона на первом этапе присваивает стратегиям a , b , c баллы 998, 1003, 999 соответственно и удаляет стратегию a из набора. На втором этапе стратегиям b , c присваиваются баллы 502, 498 соответственно и устраняется стратегия c . Остается только стратегия b .

Метод попарного удаления на первом этапе присваивает стратегиям a , b , c баллы 998, 1003, 999 соответственно и удаляет стратегию a из набора. На втором этапе стратегиям b, c присваиваются баллы 502, 498 соответственно и устраняется стратегия c . Остается только стратегия b .

В результате должна быть выбрана стратегия b , которая и была выбрана в результате работы программы (см. рис. 1).

Эксперимент 2. Пусть имеется многоагентная система, состоящая из 7 агентов. Предпочтения агентов имеют следующий вид:

• –    3 агента выбрали предпочтения a >  b >  c ;

• –    2 агента выбрали предпочтения b >  c >  a ;

• –    1 агент выбрал предпочтения b >  a >  c ;

• –    1 агент выбрал предпочтения c >  a >  b .

В данном случае оптимальной стратегией является стратегия a , которая выбрана в качестве приоритетной для наибольшей группы агентов – 3 агентов, а также является второй по приоритетности еще для двух групп по одному агенту.

Метод голосования множества должен присвоить стратегиям a , b , c баллы 3, 3, 1 соответственно и выбрать стратегии a и b .

Метод голосования множества с устранением на первом этапе присваивает стратегиям a , b , c баллы 3, 3, 1 соответственно и удаляет стратегию c из набора. На втором этапе стратегиям a и b присваиваются баллы 4 и 3 соответственно и устраняется стратегия b . Остается только стратегия c .

Метод Борда должен присвоить стратегиям a , b , c баллы 8, 9, 4 соответственно и выбрать стратегию b .

Метод Ненсона на первом этапе присваивает стратегиям a , b , c баллы 8, 9, 4 соответственно и удаляет стратегию c из набора. На втором этапе стратегиям a , b присваиваются баллы 4 и 3 соответственно и устраняется стратегия b . Остается только стратегия a.

Метод попарного удаления на первом этапе присваивает стратегиям a , b , c баллы 8, 9, 4 соответственно и удаляет стратегию c из набора. На втором этапе стратегиям a , b присваиваются баллы 4 и 3 соответственно и устраняется стратегия b . Остается только стратегия a .

В результате должна быть выбрана стратегия a , которая и была выбрана в результате работы программы (см. рис. 2).

На основе результатов проведенных экспериментов можно сделать вывод о том, что в каждом методе принятия решений есть возможность выбора неоптимальных стратегий (существуют ситуации, когда выбор метода не является оптимальной стратегией).

Вариантом решения этой проблемы является использование нескольких методов

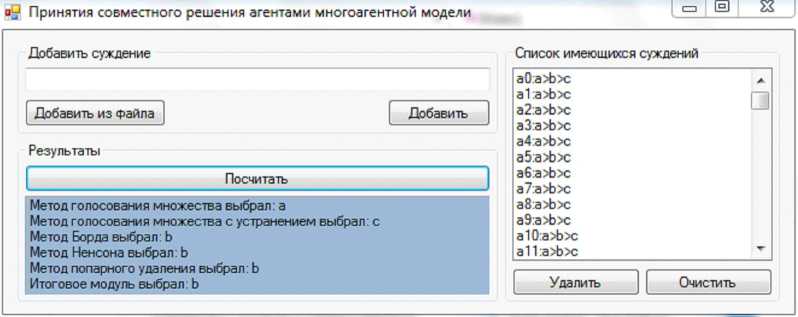
Рис. 1. Результаты эксперимента 1 (экранная копия)

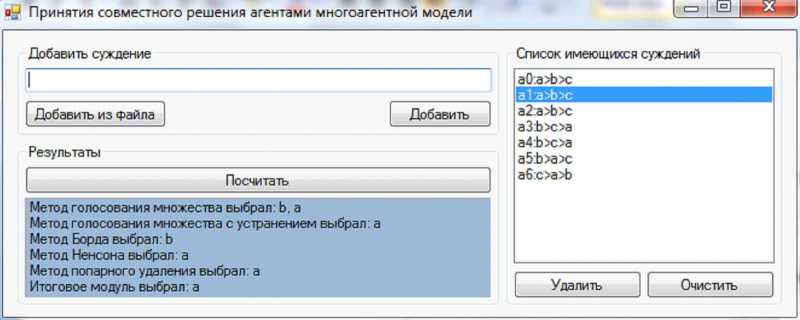
Рис. 2. Результаты эксперимента 2 (экранная копия)

принятия решений одновременно, что сводит к минимуму вероятность выбора неоптимальных стратегий.