Исследование погрешностей формирования дифракционной решетки на торце галогенидного ик-волновода

Совершенствование методов изготовления дифракционных оптических структур открывает широкие возможности по управлению световыми полями, как в волноводах, так и в свободном пространстве. Наряду с недавно появившимися оптическими структурами (фотонные кристаллы, волноводные структуры и др.) не теряют актуальности и бинарные дифракционные решетки. Кроме традиционных областей применения такие решетки интересны в качестве тестовых структур при апробации различных технологических процессов изготовления микрорельефа. Отличаясь простотой, бинарные решетки позволяют в наиболее явном виде выявлять несовершенства изготовления микрорельефов. Например, развивая технологию формирования дифракционного микрорельефа на торце поликристаллического ИК-све-товода [1], авторы выбрали бинарную решетку в качестве основной тестовой структуры. Результаты натурных экспериментов, приведенные в [1], демонстрируют необходимость совершенствования используемой технологии и побуждают к исследованию формируемого микрорельефа и моделированию его работы, чему и посвящена предлагаемая статья.

Технология горячей штамповки дифракционного микрорельефа на торце PIR-световода из галогенидов серебра была предложе- на в [1] и заключается в изготовлении матрицы решетки методом фотолитографии и собственно штамповке микрорельефа. Указанный процесс обладает недостатками, присущими с одной стороны химическому травлению (изотропия процесса и связанный с ней клин травления) и штамповке на галоге-нидном материале (термическая и механическая деформации матрицы, усадка материала) – с другой стороны.

При моделировании прохождения излучения через дифракционную решетку с технологическими погрешностями микрорельефа применяется широкий спектр методов. Так, в работе [2] предлагается метод определения интенсивностей дифракционных порядков, основанный на скалярной теории света. Исследуя решетки с субволновыми неоднородностями, применяют более строгие подходы, основанные на электромагнитной теории [3, 4]. Среди них наибольшую популярность в последнее время приобретает метод разностного решения уравнений Максвелла [5] (FDTD method), характеризующийся высокой точностью и простотой реализации. Результаты численного моделирования, представленные в настоящей работе, получены посредством этого метода.

Рассмотрев в первой части статьи особенности формирования микрорельефа бинарной дифракционной решетки на торце

PIR-световода, авторы выделяют основные типы технологических погрешностей. Во второй части оценивается отдельное и совокупное влияние таких погрешностей на формирование решеткой требуемого распределения интенсивностей.

Формирование бинарной дифракционной решетки на торце галогенидного ИК-волновода

Нанесение рельефа дифракционного оптического элемента непосредственно на торец волновода позволяет избежать юстировки оптических систем ввода/вывода излучения, совмещая их в одной структуре [6, 7]. Кроме того, указанное совмещение уменьшает потери на френелевское отражение и способствует миниатюризации оптической системы.

С учетом оптической плотности сердечника PIR-световода ( n =2,15) и длины волны каналируемого излучения (л=10,6 мкм), расчетные параметры формируемой светоделительной бинарной решетки выбирались следующими [1]: период d =30 мкм, высота рельефа h₀ =4,6 мкм, ширина ступеньки - половина периода.

Формирование микрорельефа решетки производилось в два этапа: изготовление матрицы с помощью фотолитографии и перенос рельефа с матрицы на торец волновода термической штамповкой.

Изготовление матрицыпо фотолитографической технологии

Микрорельеф матрицы формировался посредством фотолитографического процесса [8,9,10]. Стеклянные подложки оптического качества очищались от органических загрязнений с помощью концентрированного раствора щелочи, после чего промывались в дистиллированной воде. Удаление неорганических загрязнений производилось путем кипячения подложек в растворе серной кислоты с добавлением двухромовокислого калия в течение 2 часов, с последующим промыванием дистиллированной водой. Очищенные подложки сушились в муфельной печи, для улучшения адгезии на их поверх- ность наносился в вакууме адгезив (праймер) [10].

Фоторезист марки ФП3513 наносился на обработанную поверхность центрифугированием на скорости 4000 об/мин. в течение 20-30 секунд. Толщина слоя фоторезиста варьировалась по площади подложки в пределах 1,0-1,1 мкм. Сушка производилась в печи при температуре 850С. Далее подложка с нанесенным фотослоем засвечивалась УФ-излучением через фотошаблон в установке совмещения и экспонирования ЭМ-5006. Время экспонирования выбиралось в зависимости от толщины фотослоя и составляло 45-50 с.

Проявка осуществлялась 1-2 минуты в стандартном щелочном проявителе. После промывки полученная подложка с проявленным изображением на фотослое подвергалась двухступенчатому термозадубливанию при температуре 120-180 С°.

Воспроизведенное изображение в слое фоторезиста переносилось на стеклянную подложку с помощью жидкостного химического травления плавиковой кислотой. Концентрация раствора подбирались таким образом, чтобы обеспечить достаточно высокую скорость травления стекла при максимальной стойкости фоторезиста. Во время травления раствор перемешивался. Процесс периодически контролировался анализатором и занимал от 10 до 15 мин.

Подготовка матрицы завершалась удалением фотомаски этилацетатом и промыванием подложки дистиллированной водой.

Перенос рельефа решеткис матрицы на торец волновода

Для штамповки рельефа на торце PIR-световода собиралась установка, объединяющая в себе микроскоп, телекамеру, трехкоординатный столик и нагревательное устройство с цифровым контролем температуры.

Сама штамповка заключалась в совмещении матрицы с торцом волновода и выдавливании рельефа на его торце. Давление штамповки подбиралось равным 0,3 кГ/мм2 для волокна с радиусом R=700 мкм (радиус сердечника r=420 мкм). Темпера- тура нагревательного элемента задавалась в диапазоне 240 - 3900 С. При этом в зоне штамповки из-за конечной теплопроводности стеклянной матрицы и теплообмена с окружающей средой температура несколько понижалась. Контроль качества сформированной на торце волновода поверхности осуществлялся с помощью автоматического интерферометра “Zygo”.

Изучив технологические погрешности формирования микрорельефа, авторы разделили их на “локальные” и “глобальную”. К “локальным” были отнесены ошибки, заметные при исследовании одного периода решетки (рис. 1): в получении заданной высоты микрорельефа (недотрав или перетрав) и наличие клинов травления по обе стороны ступеньки формируемой бинарной решетки. К “глобальной” технологической погрешности, выявленной при изучении профилограммы всей решетки (рис. 2), авторы отнесли общий прогиб профиля.

Ось абсцисс направлена поперек штрихов решетки, по оси ординат откладывается высота профиля.

Отклонения высоты профиля решетки от расчетной связаны с ошибками в определении длительности травления матрицы. При недостаточном времени травления высота оказывалась ниже расчетной (недотрав), при избыточном – выше (перетрав). При расчетной высоте профиля в 4,6 мкм, высота формируемого рельефа варьировалась от 4,0 до 5,2 мкм.

Образование клина травления объясняется изотропией химических процессов и аморфностью подложки. Острый угол между плоскостью торца и подъемом клина (характеризующий клин травления) для представленной технологии варьировался в интервале 36-440 .

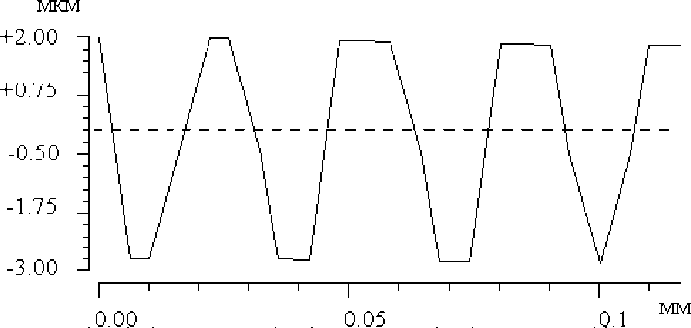
Рис. 1. Профилограмма участка решетки, полученная с помощью интерферометра “Zygo”.

Ось абсцисс направлена поперек штрихов решетки, по оси ординат откладывается высота профиля. Пунктирная линия соответствует нулевой отметке высоты микрорельефа

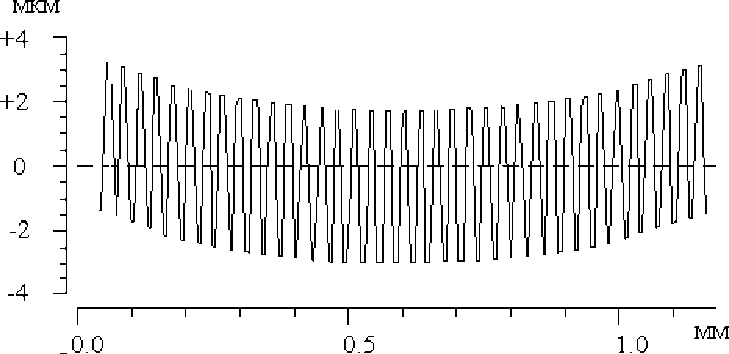
Рис. 2. Профилограмма всей решетки, полученная с помощью интерферометра “Zygo”.

Прогиб профиля решетки, на наш взгляд, происходит из-за различия в структуре материалов сердечника и оболочки PIR-световода и деформации матрицы. Величина прогиба g в экспериментах сильно зависела от температурного режима штамповки и оказываемого на торец давления. Для настоящей технологии она варьировалась от 0,3 до 2 мкм в центре волновода.

Таким образом, выбор режимов в представленной технологической цепочке определяется не только характеристиками используемых материалов, но и приемлемостью величин отклонения от прямоугольного профиля решетки. Оценка влияния выявленных технологических погрешностей на формирование распределения интенсивностей дифракционных порядков проводилось методом вычислительного эксперимента.

Исследование влияния технологических погрешностей изготовления бинарной решетки на формирование распределения интенсивностей дифракционных порядков

Моделирование распространения электромагнитного излучения через дифракционные решетки с различными технологическими погрешностями микрорельефа проводилось посредством разностного решения уравнений Максвелла [5]. За основу принимался алгоритм, сформулированный в [4], дополненный наложением поглощающих слоев [11] и новой методикой формирования падающей волны [12]. При этом полагалось, что из среды ( n =2,15) на дифракционную поверхность падает плоская однородная Н-волна ( λ =10,6 мкм). Результатами моделирования считались значения интенсивностей прошедших пяти дифракционных порядков: I₀, I₁, I_-1, I₂, I_-2 (нулевого, первого, минус первого, второго, минус второго).

Верификация полученных результатов проводилась проверкой выполнения закона сохранения энергии. Для этого дополнительно находились интенсивности отраженных порядков, и все интенсивности складывались вместе. В представленных ниже вычисли- тельных экспериментах отклонение суммы интенсивностей от интенсивности падающей волны составляло менее одного процента.

Влияние недотрава, перетрава и клина травления

Отдельно изучая влияние недотрава и перетрава ступеньки бинарной решетки, рассмотрим результаты моделирования, представленные в табл 1. Длина волны излучения предполагалась равной 10,6 мкм. Для решетки, лишенной указанных недостатков ( h₀ =4,6 мкм), в первый и минус первый прошедший порядки направляется 69% энергии падающего пучка, в нулевой, второй и минус второго порядки – по 1,63%. Можно говорить о хороших светоделительных показателях идеально изготовленной решетки. Исследуя случаи перетрава и недотрава по табл. 1, можно сделать вывод о предпочтительности пере-трава над недотравом, характеризующимся не только меньшей суммарной энергией первого и минус первого порядков (65% для h =4,0 мкм по сравнению с 67% для h =5,2 мкм), но и существенно большим количеством энергии, направляющейся в нулевой порядок (7,16% по сравнению с 2,67%). Таким образом, хотя суммарная энергия рабочих порядков (первого и минус первого) снижается несущественно (на 4% от общей энергии падающей волны), при недотраве становится заметным влияние нулевого порядка (возрастает с 1,63% до 7,16%).

К рассмотренной технологической по-

Таблица 1. Зависимость распределения энергии прошедшей волны по дифракционным порядкам от высоты профиля прямоугольной решетки для расчетной высоты h ₀ =4,6 мкм, длина волны л=10,6 мкм

высота профиля h, мкм интенсивности дифракционных порядков I0 I1=I-1 I2=I-2 4,0 0,0716 0,3244 0,0111 4,2 0,046 0,3349 0,0126 4,4 0,0275 0,3417 0,0143 4,6 0,0163 0,345 0,0163 4,8 0,0125 0,3448 0,0184 5,0 0,016 0,341 0,0208 5,2 0,0267 0,3339 0,0234 грешности добавим клин травления, приняв характеризующий его угол равным 400. Результаты моделирования, представленные в табл. 2, свидетельствуют о существенном влиянии клина травления на распределение интенсивностей. Так, в случае точно выдержанной высоты профиля (h0=4,6 мкм) добавление клина уводит из рабочих порядков четверть энергии падающей волны, а в нулевом порядке появляются лишние десять процентов такой энергии. Недотрав не ухудшает распределение энергии по первому и минус первому порядкам, но доводит долю энергии в нулевом порядке до 17,28%, что уже не позволяет говорить о такой решетке как о светоделительной. При максимальном перетра-ве доля энергии, ушедшей в нулевой порядок, не увеличивается, однако, сокращается до 37% суммарная энергия рабочих порядков (при h0 она составляла 45%), что опять не позволяет считать светоделительное свойство решетки удовлетворительным.

Таким образом, при необходимости сократить энергетические потери в первом и минус первом дифракционном порядках от клина травления, предпочтительнее допустить недотрав матрицы. Перетрав же характеризуется меньшим значением интенсивности нулевого порядка.

Влияние прогиба решетки

Отработанная технология изготовления матрицы позволит избежать как появления клина травления, так и погрешностей откло-

Таблица 2. Зависимость распределения энергии прошедшей волны по дифракционным порядкам от высоты профиля прямоугольной решетки с клином травления для расчетной высоты h ₀ =4,6 мкм, длина волны л=10,6 мкм

высота профиля h, мкм интенсивности дифракционных порядков I0 I1=I-1 I2=I-2 4,0 0,1728 0,2324 0,02796 4,2 0,1453 0,236 0,02827 4,4 0,13 0,2317 0,02896 4,6 0,1196 0,2241 0,02874 4,8 0,1141 0,2134 0,02778 5,0 0,1142 0,2 0,02601 5,2 0,1177 0,1858 0,02433 нения высоты микрорельефа от требуемой. Однако, получив в распоряжение даже точно выполненную матрицу, исследователь будет наблюдать “глобальную” технологическую погрешность – прогиб профиля решетки, возникающий при штамповке рельефа на торце PIR-световода.

Основываясь на результатах численного моделирования работы решетки, изготовленной с идеальной матрицы (табл. 3), сделаем заключение о небольшом влиянии прогиба профиля на распределение интенсивностей прошедших порядков. Даже в случае предельной величины прогиба ( g =2,0 мкм) суммарные энергетические потери в первом и минус первом порядках составили всего 12%, что вдвое меньше потерь от появления клина травления при точно выдержанной высоте профиля и отсутствии прогиба. Решетка продолжает демонстрировать хорошие светоделительные характеристики: интенсивности нулевого, второго и минус второго порядков не меняются (табл.3) при выбранных значениях g .

Добавление клина травления и варьирование высоты профиля при максимальном прогибе (табл. 4) существенно сказываются на распределении энергии по порядкам по сравнению с предыдущей серией экспериментов (табл. 3). Однако, оценивая влияние именно прогиба и сравнивая с результатами аналогичной серии вычислительных экспе

Таблица 3. Зависимость распределения энергии прошедшей волны по дифракционным порядкам от глубины прогиба профиля решетки, изготовленной с идеальной матрицы

глубина прогиба g, мкм	интенсивности дифракционных порядков
	I 0	I 1 = I -1	I 2 = I -2
0,2	0,0142	0,3487	0,0164
0,4	0,0142	0,347	0,0163
0,6	0,0141	0,3435	0,0162
0,8	0,014	0,34	0,016
1,0	0,0138	0,3328	0,0156
1,2	0,0136	0,326	0,0152
1,4	0,0134	0,3183	0,0147
1,6	0,0131	0,3082	0,0142
1,8	0,0127	0,2993	0,0136
2,0	0,0123	0,2859	0,0128

Таблица 4. Зависимость распределения энергии прошедшей волны по дифракционным порядкам от высоты профиля прямоугольной решетки с клином травления и предельной глубиной прогиба

высота профиля h, мкм интенсивности дифракционных порядков I0 I1=I-1 I2=I-2 4,0 0,1295 0,1921 0,0211 4,2 0,1116 0,1912 0,0206 4,4 0,1025 0,1844 0,0204 4,6 0,0974 0,175 0,0197 4,8 0,0969 0,1631 0,0186 5,0 0,0996 0,1506 0,0176 5,2 0,1048 0,1384 0,0169 риментов с решеткой без прогиба (табл. 2), отметим, что из рабочих порядков ушло дополнительно не более десяти процентов энергии (независимо от высоты профиля). При этом поведение значений интенсивностей нулевого порядка (табл. 4) по сравнению с результатами из табл. 2 сильно не ухудшилось.

Необходимо признать, что решетка, сочетающая “глобальную” и “локальные” погрешности изготовления, обладает низкими светоделительными характеристиками. Особенно это относится к случаю предельного перетрава, когда прошедшая энергия почти равномерно распределяется между нулевым, первым и минус первым порядками (10,48%, 13,84% и 13,84%). Более того, от такого профиля отражается 58,46% падающей энергии, что приводит к значительному нагреванию PIR-световода.

Следует признать решающий вклад в искажение распределения интенсивностей за клином травления. Дальнейшие усилия по совершенствованию технологического процесса необходимо сосредоточить на недопущении появления указанного клина, или, по крайней мере, уменьшении значения угла, характеризующего отклонение боковых стенок рельефа от вертикали, что возможно, например, при использовании технологии плазмохимического травления для изготовления матрицы [9].

Выводы

Предложенная в [1] технология нанесения дифракционного микрорельефа позволила сформировать светоделительную бинар- ную решетку на торце PIR-световода из галогенидов серебра. В данной статье приведена оценка качества формирования упомянутой структуры, которая производилась посредством профилометрического исследования поверхности торца, выявившего характерные технологические погрешности изготовления. Исследование влияния таких погрешностей на формирование решеткой заданного распределения интенсивностей проводилось методом вычислительного эксперимента на основе разностного решения уравнений Максвелла.

В результате анализа данных, полученных численным моделированием, сформулированы рекомендации по улучшению технологии формирования дифракционных элементов на торце галогенидного ИК-волновода.

Работа выполнена при поддержке грантов РФФИ N 07-01-97606-р-офи, 07-07-97601-р-офи и 06-07-08074, гранта Президента РФ MД-4003.2005.9, а также Российско-американской программы “Фундаментальные исследования и высшее образование” (BRHE, CRDF-project N RUXO-014-SA-06).