Исследование погрешностей моделирования сигмоидальной функцией сигналов полимеразной цепной реакции в реальном времени

В статьях [1, 2] приведена классификация методов определения значения порогового цикла — величины, позволяющей судить об исходном количестве копий ДНК и сравнивать образцы между собой по результатам ПЦР. Показаны преимущества вычисления пороговых циклов методом моделирования на базе сигмоидальной функции (МСФ) [3, 4]. При рассмотрении погрешностей измерения порогового цикла [2] шумы моделировались последовательностью 50 случайных чисел, соответствующих 50 температурным циклам. Было показано, что такая шумовая последовательность одновременно действует на все участки сигнала ПЦР и вызывает случайное изменение порогового цикла. В настоящей статье для детального изучения особенностей МСФ предложено использовать нормированное изменение интенсивности флуоресценции в течение одного или нескольких циклов (импульсное возмущение).

ИССЛЕДОВАНИЕ ВЛИЯНИЯ НА ПАРАМЕТРЫ МСФ НОРМИРОВАННОГО ИЗМЕНЕНИЯ

ИНТЕНСИВНОСТИ ФЛУОРЕСЦЕНЦИИ В ТЕЧЕНИЕ ОДНОГО ЦИКЛА

Нормированное изменение интенсивности флуоресценции F i в течение одного цикла можно представить как единичную выборку шумового сигнала с нормированной максимальной амплитудой. Возникающие при этом изменения параметров МСФ можно рассматривать в качестве одной из причин погрешностей измерения пороговых циклов.

Для реализации нормированного изменения интенсивности использованы аналитическая фор- ма и методика построения модернизированной МСФ, приведенные в статье [5]:

F = F m / (1+exp (( С 0 – C ) / k )) +

+ f 0 + f 1 · C + f 2 · C ², (1)

где F — интенсивность флуоресценции, измеряется в относительных единицах флуоресценции (о.е.); F m — максимальное изменение интенсивности флуоресценции в конце реакции; С — порядковый номер цикла амплификации; С 0 — дробный номер цикла, при котором интенсивность флуоресценции достигает половины значения F m ; k — коэффициент, который определяется наклоном кривой; f 0 — смещение нулевой линии (фон детектора); f 1 — коэффициент, который определяется линейным дрейфом нулевой линии; f 2 — коэффициент, учитывающий квадратичную составляющую дрейфа нулевой линии.

Вычисления параметров МСФ выполнялись с помощью электронной таблицы Excel (табл. 1) в следующей последовательности.

• 1.    В ячейках В11:В60 вычислялась исходная МСФ с параметрами, приведенными в ячейках В4:В7 , как зависимость от номера цикла в ячейках А11:А60 (рис. 1, а).

• 2.    В ячейках С11:С60 вычислялась исходная МСФ с аналогичными параметрами, первоначально расположенными в ячейках С4:С7 .

• 3.    В ячейку D11 вносилось нормированное изменение интенсивности флуоресценции в течение первого цикла F 1 = 100 о.е. (относительных единиц флуоресценции). В ячейках E11:E60 вычислялись суммы (В11+D11):(В60+D60) . В ячейках F11:F60 вычислялись квадраты разностей (Е11-С11)²:(Е60-С60)² , а в ячейке С10 — сумма квадратов разностей S k .

  Табл. 1 . Электронная таблица для вычисления параметров МСФ

  	A	B	C	D	E	F
  1	i=		1	15
  2	Уровень=	500	500	500
  3	C ti =	23,500	23,490	23,515
  4	C 0i =	23,5	23,465	23,548
  5	F m =	1000	1024,976	976,255
  6	k =	1,39	1,439	1,338
  7	f 0 =	0	25,951	-5,815
  8	f 1 =	0	-2,571	1,383
  9	f 2 =	0	0,032	-0,016
  10	S k =	0	7663,986	8916,995
  11	1	9,33E-05	23,414	100	100,0001	5865,656
  25	15	2,204	2,57537	0	2,204367	22,845
  33	23	411,029	414,080	0	411,029	9,306
  34	24	588,971	589,243	0	588,971	0,074
  43	33	998,925	999,496	0	998,9251	0,326
  60	50	1000	1002,188	0	1000	4,789

  
  

• 4.    После установления условия минимального значения S k и оптимизации параметров в ячейках С4:С9 по методу наименьших квадратов в ячейках С11:С60 получаются числовые значения оптимизированной модели при номере цикла в ячейке А11 i = 1.

• 5.    Аналогичные действия выполнялись при установке величины F i = 100 о.е. последовательно в ячейки D12:D60 ( i = 2–50). В ячейках С4:С9 каждый раз получаются новые параметры МСФ .

Целью построения моделей является определение величин С 0 i , которые можно принять в качестве новых значений пороговых циклов с учетом нормированных изменений интенсивности флуоресценции (этот метод определения пороговых циклов можно назвать условно методом "средней точки").

В графическом виде результаты изменения величины С 0i в зависимости от номера цикла i , в который вносилось нормированное изменение флуоресценции, представлены на рис. 1, б (ряд 1). На этом графике нулевое значение на вертикальной оси соответствует величине С 0 = 23.5 исходной модели. Наибольшие изменения величины С 0 i , приблизительно равные 0.17, наблюдаются при положении нормированного изменения флуоресценции в 23-м и 24-м циклах, т. е. в средней части исходной МСФ, график которой приведен на рис. 1, а.

Если в ячейки D11:D60 табл. 1 последовательно вносить величину F i = -100 о.е., то изображение графика, приведенного на рис. 1, становится зеркальным по отношению к горизонтальной оси.

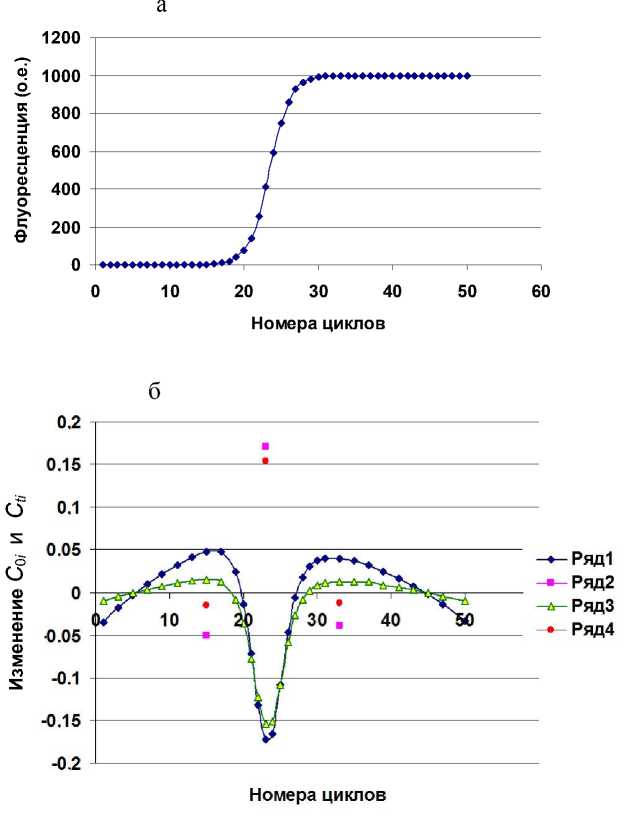
Рис. 1. Графики зависимостей параметров МСФ от номера температурного цикла.

а — исходная МСФ при f 0 = f 1 = f 2 = = 0 о.е., Fm = = 1000 о.е.; б — зависимости величин С 0 i и С ti от номера цикла i внесения нормированного изменения флуоресценции

Несколько точек этого графика, соответствующие 15-му, 23-му и 33-му циклам, приведены на рис. 1, б (ряд 2).

ОПРЕДЕЛЕНИЕ ПОРОГОВОГО ЦИКЛА МЕТОДОМ ПОРОГА

Для реализации метода порога в ячейку С3 табл. 1 добавлена величина порогового цикла С ti . Величина С ti определяется на уровне 500 о.е., приведенном в ячейке C2 (оптимальный уровень порога [2]). При этих вычислениях использованы параметры МСФ в соответствии с формулой

C2 =

=$C$7+$C$5/(1+EXP(($C$4-C3)/$C$6))+ +$C$8*C3+$C$9*(C3)^A2 .               (2)

Применен инструмент "Поиск решения" из меню "Сервис" ; при этом выполнялись следующие действия:

"Установить целевую ячейку С2" , "Равной значению 500" , "Выполнить" , "Изменяя ячейки С3" .

График изменения величины С ti в зависимости от номера цикла i , в который вносилось нормированное изменение флуоресценции F i = 100 о.е., представлен на рис. 1, б (ряд 3). Несколько точек графика при величине F i = -100 о.е. приведены на рис. 1, б (ряд 4). При сравнении графиков 3 и 1 рядов на рис. 1, б, можно отметить, что изменения величин С ti при внесении нормированного изменения флуоресценции меньше, чем изменения величин С 0 i при тех же условиях.

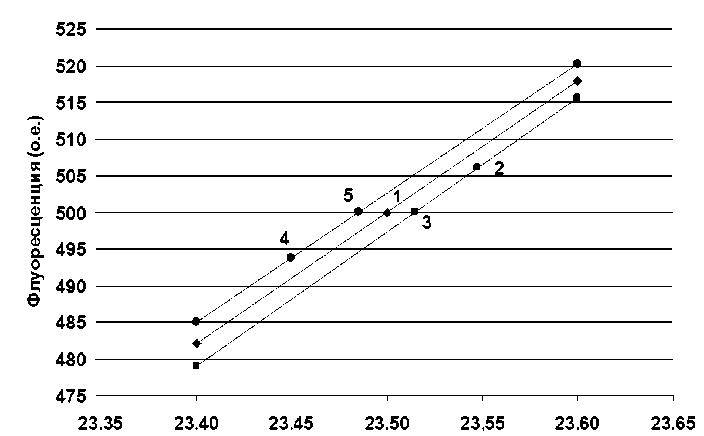
Рис. 2. Графики зависимости интенсивности модельных сигналов от дробного номера цикла.

Пояснения в тексте

Дробный номер цикла

ЭФФЕКТ УМЕНЬШЕНИЯ ПОГРЕШНОСТЕЙ ПРИ ИСПОЛЬЗОВАНИИ МЕТОДА ПОРОГА

С целью сравнения механизмов вычисления пороговых циклов методом порога С t и методом "средней точки" С 0 на рис. 2 приведены графики флуоресценции в диапазоне от 23.4 до 23.6 дробных единиц циклов (д.е.ц.); при этом интенсивность флуоресценции вычислялась с использованием формулы (2).

Средний график соответствует исходной модели с параметрами, приведенными в ячейках В4:В9 табл. 1. Точка 1 соответствует параметрам, приведенным в ячейках В2:В4 , при этом номера пороговых циклов равны: С 0 = С t = 23.5. Нижний график построен при условии F 15 = 100 о.е. (внесение нормированного изменения в величину флуоресценции 15-го цикла) при параметрах, приведенных в ячейках D4:D9 ; точка 2 имеет координаты С 015 = 23.548 д.е.ц. и F 2 = 506.025 о.е., а точка 3 — С t 15 = 23.515 д.е.ц. и F 3 = 500 о.е. Верхний график построен при условии F 15 = -100 о.е., точке 4 соответствует С 0 = 23.450 д.е.ц., а точке 5 — С t = 23.485 д.е.ц.

Сравнивая координаты точек 1 и 2, можно отметить, что нижний график смещен относительно среднего исходного графика, нормированного при f 0 = 0 и F m = 1000 о.е., по горизонтальной оси на величину 0.048 д.е.ц. и по вертикальной оси на величину 6.025 о.е.

Выгодно вместо величины С015 (точка 2) в качестве порогового цикла использовать величину Сt15 (точка 3), поскольку в таком случае не учитывается перемещение графика по вертикальной оси, по- этому влияние внесенного нормированного изменения флуоресценции на результат определения порогового цикла значительно уменьшается (в приведенном примере более чем в 3 раза). Аналогичный вывод можно сделать при рассмотрении координат точек 4 и 5 верхнего графика.

Усредненные вносимые изменения пороговых циклов можно сравнить путем вычисления значений стандартного отклонения S величин C_ti и С 0 i в пределах от 1 до 50 циклов: S ( C ti ) = 0.049 и S ( С 0 i ) = = 0.061 соответственно для метода порога на уровне 500 о.е. и метода "средней точки".

Стандартное отклонение S величин C ti и С 0 i можно рассматривать как основную составляющую погрешностей измерения пороговых циклов, при этом метод порога имеет преимущество по сравнению с методом "средней точки" ( S ( С ti ) < <  S ( С 0 i )).

ИССЛЕДОВАНИЕ ВЛИЯНИЯ НА ПАРАМЕТРЫ МСФ НОРМИРОВАННОГО ИЗМЕНЕНИЯ

ИНТЕНСИВНОСТИ ФЛУОРЕСЦЕНЦИИ В ТЕЧЕНИЕ НЕСКОЛЬКИХ ЦИКЛОВ

Если при каждых циклах i и ( i +1) последовательно внести нормированные изменения флуоресценции F i = F i +1 = 100 о.е., то с помощью табл. 1 можно вычислить новые параметры МСФ . Результаты вычисления зависимостей изменения величин С 0 i и С ti от номера цикла i приведены на рис. 3 (соответственно ряды 1 и 2). На этом графике нулевое значение на вертикальной оси соответствует величине С 0 = С t = 23.5 исходной модели.

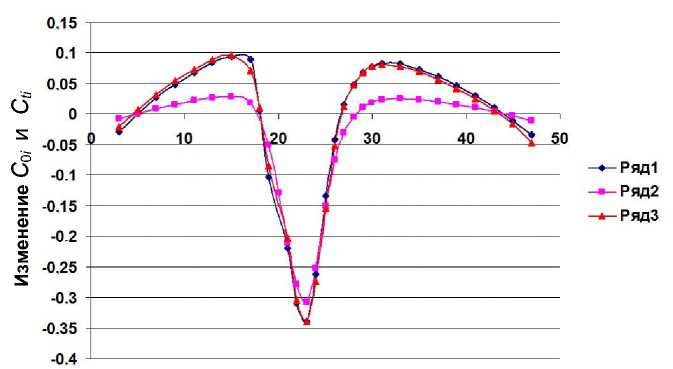
Номера циклов

Рис. 3. Графики зависимостей величин С 0 i и С ti от номера цикла i при воздействии нормированного изменения интенсивности флуоресценции в течение двух циклов

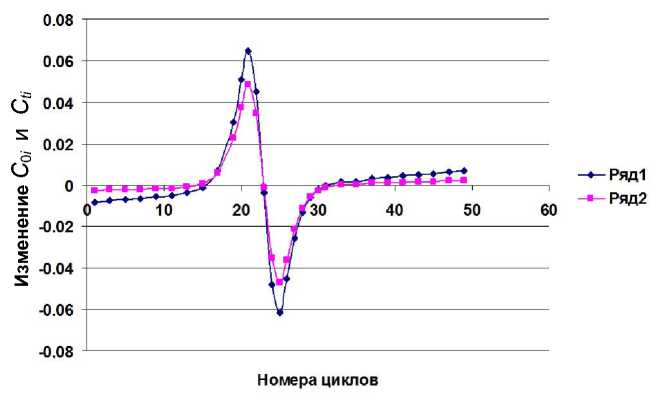
Рис. 4. Графики зависимостей величин С 0 (ряд1) и С t (ряд2) от номера цикла i при F i = 100 о.е. и F i +1 = -100 о.е.

Если сравнить графики на рис. 3 и рис. 1, б (ряд1), то можно отметить, что максимальное изменение 23-го цикла с 2 импульсами, равное –0.338 д.е.ц., почти в 2 раза больше, чем максимальное изменение с 1 импульсом, которое равно –0.173 д.е.ц.

На рис. 3 (ряд3) приведен результат сложения со сдвигом на 1 цикл двух одинаковых зависимостей С 0 i , полученных при воздействии нормированного изменения интенсивности флуоресценции в течение одного цикла. Почти полное совпадение графиков рис. 3 (ряд1 и ряд3) позволяет сделать вывод об аддитивности результатов воздействия нормированных изменений интенсивности флуоресценции в течение нескольких циклов.

Этот вывод с учетом знака подтверждается зависимостями изменения величин С0i и Сti от номера цикла i, когда при каждом i-м цикле вносилось нормированное изменение флуоресценции Fi = = 100 о.е., а при следующем цикле вносилось нор- мированное изменение флуоресценции Fi+1 = = -100 о.е. Графики этих зависимостей приведены на рис. 4.

Наибольшие изменения величин С 0 i , приблизительно равные ±0.06 д.е.ц., наблюдаются при i = = 21 и 25 циклам. Эти изменения почти в 3 раза меньше, чем максимальное изменение с одиночными импульсами, равное -0.173 д.е.ц. Изменения величин С 0 i по амплитуде почти полностью совпадают с результатами вычитания двух числовых последовательностей изменений С 0 i со сдвигом на 1 цикл.

СРАВНЕНИЕ ВЛИЯНИЯ НА ПАРАМЕТРЫ МСФ ШУМА И НОРМИРОВАННОГО ИЗМЕНЕНИЯ ИНТЕНСИВНОСТИ ФЛУОРЕСЦЕНЦИИ

Шумовые сигналы дискретно моделировались 10 последовательностями по 50 случайных чисел с максимальными амплитудами F iM , равными ±1,

±10 и ±100 о.е. Эти последовательности поочередно вносились в ячейки D12:D60 , затем вычислялись величины С 0 и С t .

Значения стандартного отклонения S позволяют оценить усредненные погрешности измерения пороговых циклов, возникающие при воздействии на МСФ шума и нормированного изменения интенсивности флуоресценции в течение одного цикла. Значения S величин С 0 и С t для каждой серии из 10 последовательностей случайных чисел приведены в табл. 2 (столбцы 2–4). По результатам сравнения величин S , полученных при дополнительной обработке сигналов, можно оптимизировать измерения пороговых циклов.

В столбце 5 табл. 2 приведены значения S величин С 0 и С t для случая предварительной обработки шумовых сигналов с помощью фильтра 3С3 (трехкратное последовательное применение скользящего среднего значения — прямоугольное окно по 3 циклам [1]). В последнем столбце приведены величины S по 50 циклам при нормированном изменении интенсивности флуоресценции в течение одного цикла без фильтра.

Значение S при шуме ±100 о.е. можно сравнить со значением S при нормированном изменении интенсивности флуоресценции в течение одного цикла F i = 100 о.е. в виде отношения

Е = S ( С 04 ) / S ( С 06 ) = 0.252 / 0.061 = 4.13.

Величину Е можно условно назвать "коэффициентом эффективности шума", поскольку эта величина характеризует увеличение воздействия нормированной шумовой последовательности в течение всех циклов МСФ по отношению к воздействию нормированного изменения интенсивности флуоресценции в течение одного цикла. После фильтрации эффективность шума уменьшается:

Е ф = S ( С 05 ) / S ( С 06 ) = 0.213 / 0.061 = 3.49.

При сравнении полученных результатов видно, что величины S приблизительно линейно зависят от уровня шума (столбцы 2–4 табл. 2). Значение S величины С 0 , равное 0.252, после фильтрации уменьшается на 15 % (0.213 / 0.252 = 0.85). Отношение значений S величин С t и С 0 меньше единицы на 12 % (0.222 / 0.252 = 0.88).

При одновременном использовании метода порога и фильтрации сигналов влияние шума уменьшается еще больше. Отношение значений S величин С t ( с фильтром) и С 0 (без фильтра) меньше единицы на 22 %:

S ( С t 5 ) / S ( С 04 ) = 0.197 / 0.252 = 0.78.

ЗАКЛЮЧЕНИЕ

Предложена методика исследования особенностей МСФ с помощью нормированного изменения интенсивности флуоресценции в течение одного температурного цикла (импульсного возмущения). С помощью численного эксперимента показано, что максимальная погрешность определения пороговых циклов получается при импульсном воздействии на склоне МСФ .

Приведены результаты импульсного возмущения на МСФ в течение нескольких циклов. Показано, что эти результаты могут быть получены путем сложения результатов воздействия единичных импульсных воздействий с учетом знака. Аддитивность результатов позволяет рассматривать шум как эквивалент последовательности случайных импульсов.

Выполнено сравнение влияния на параметры МСФ шума и импульсного воздействия в течение одного цикла. Приведено определение "коэффициента эффективности шума".

Табл. 2. Результаты вычислений стандартного отклонения S величин С 0 и С t в зависимости от вида и величины воздействия

Стандартное отклонение S величин С 0 , С t	Вид и величина воздействия
	Шум FiM = = ±1 о.е.	Шум F iM = = ±10 о.е.	Шум F iM = = ±100 о.е.	Шум F iM = = ±100 о.е., фильтр	1 цикл F i = 100 о.е.
1	2	3	4	5	6
С 0	0.00185	0.019	0.252	0.213	0.061
С t	0.00176	0.018	0.222	0.197	0.049

Предложено использовать одновременно метод порога и МСФ, при этом графически пояснен механизм уменьшения погрешностей измерения пороговых циклов.

Показано, что путем использования метода порога и фильтрации сигналов при моделировании сигналов ПЦР-РВ сигмоидальной функцией можно уменьшить влияние шума на погрешность измерения пороговых циклов (в приведенном примере величина стандартного отклонения понизилась на 22 %). Этот результат реализован в программном обеспечении анализатора нуклеиновых кислот АНК-32, который серийно выпускается в ИАП РАН [6].

Работа выполнена при поддержке Министерства образования и науки Российской Федерации в рамках федеральной целевой программы "Исследования и разработки по приоритетным направлениям развития научно-технологического комплекса России на 2007– 2012 годы" при выполнении научно-исследовательской работы по лоту (шифр 2011-1.2-512-073) "Разработка макетов аппаратно-программных комплексов для лабораторной и функциональной диагностики" по теме "Разработка макета аппаратно-программного комплекса для лабораторной и функциональной диагностики широкого спектра признаков методом полимеразной цепной реакции в реальном времени" (шифр заявки 2011-1.2-512-073-110).