Исследование погрешностей определения координат наземной радионавигационной системы

В настоящее время задача определения собственного местоположения Российских судов и кораблей решается с помощью наземных радионавигационных систем (РНС) РС-10, «Марс-75» и «Брас», последние две из которых полностью выработали свой ресурс и требуют замены. Решение задачи с использованием глобальных радионавигационных систем «ГЛОНАСС» (Россия) и GPS (США) не представляется возможным из-за требуемой надежности, неполноценной группировки орбитальной части системы «ГЛОНАСС», а Соединенные Штаты Америки оставляют за собой право загрубления гражданского SA-кода над любым районом земной поверхности, что сужает сферу применения системы GPS.

Актуальной задачей является создание новой радионавигационной системы, которая соответствует современным требованиям точности, дальности действия, пропускной способности, помехозащищенности и надежности.

В наземных РНС используются методы измерения координат подвижного объекта, основанные на определении его положения относительно некоторых опорных пунктов с известными координатами с помощью поверхностей и линий положения (ЛП) [1].

Каждому фиксированному значению навигационного параметра (НП) соответствует определенная поверхность положения (на земной поверхности - линия положения). Местоположение объекта в пространстве определяется пересечением трех поверхностей положения, а на поверхности земли - двух линий положения.

В зависимости от того, какой навигационный параметр измеряется, различают следующие методы определения местоположения: пассивно-дальномерный, разностно-дальномерный, суммарно-дальномерный, квази-дальномерный.

Целью данной работы является исследование погрешностей определения местоположения в рабочей зоне наземных радионавигационных систем.

Цля достижения указанной задачи были исследованы определения теоретической погрешности в различных режимах работы РНС, алгоритмы решения на эллипсоиде прямой и обратной геодезических задач, методы расстановки расположения опорных станций (ОС) с целью уменьшения влияния геометрического фактора в рабочей зоне РНС.

Основным НП при определении местоположения является дальность, разность или сумма дальностей от бор- товой стации (БС) до опорных станций. Результат измерения можно представить в следующем виде:

R _изм , = R i + А,                    (1)

где А - погрешность измерения; R - истинное значение дальности.

Измерения дальностей R_mMi от N опорных станций для исследуемых режимов работы РНС определяются по следующим формулам:

• -    в пассивно-дальномерном вешение местоположения

R i = V ( X, - x _БС ) ² + ( Y - y _bc ) ² ;        (2)

• -    в разносно-дальномерном

R , = V ( X — X бс ) ² + ( Y — y _B c ) ² —

• —V ^{( X} ВД - ^X БС ) ^{+ (} ^Д - Y BC ) ^;

  - в суммарно-дальномерном

R , = V( X , — X БС ) ² + ( Y — Y БС ) ² + ⁺ V( X ВД - X БС ) ⁺ ( ^Y BД - ^С ) ;

- в квазидальномерном

R , = V ( X , - X БС ) ² + ( Y - Y БС ) ² + А t • С ,       (5)

где i = 1...^- текущий номер измерения дальности; А', У - координаты i-ой опорной станции;.У_БС, У_БС - координаты бортовой станции; А_ВД, У_вд - координаты ведущей станции; Ат - расхождение бортового и системного шкал времени, с - скорость распространения волн в среде.

В каждом режиме составляется система из N уравнений с двумя неизвестными и решается итерационным методом Ньютона [1] в прямоугольной проекции Гаусса-Крюгера.

Известно, что на погрешность измерения местоположения влияет геометрическое расположение опорных станций и бортовой станции, так называемый геометрический фактор, который позволяет оценить вклад в точностные характеристики взаимную ориентацию ОС и БС. Определение расположения опорных станций, при котором геометрический фактор оказывает минимальное влияние на погрешность координат в рабочей зоне РНС, является актуальной задачей.

Современное развитие вычислительных систем позволяет производить расчеты и моделирование в короткие сроки. Предварительное проведение исследований погрешностей в рабочей зоне РНС актуально в силу ряда причин.

Во-первых, опорные станции могут быть размещены только в определенных охраняемых и электрифицированных местах, поэтому антенны ОС размещают на маяках или возвышенностях для увеличения дальности действия. Таких потенциальных для размещения мест может быть несколько, и их количество обычно превышает число станций в системе. Соответственно необходимо на основа нии перечня координат опорных точек провести исследования с целью определения наилучшего взаимного расположения станций.

Во-вторых, для уменьшения погрешности определения координат могут быть развернуты мобильные и перевози мые станции, поэтому необходимо определить наилучшее место расположения дополнительных станций.

В-третьих, теоретически рассчитанная погрешность может быть представлена как «поле погрешностей», которое отображается на экране приемоиндикатора, предоставляя дополнительную информацию членам экипажа судна [2; 3].

При проведении исследований определения погрешности координат в рабочей зоне РНС использовались два метода - статистического моделирования и косвенных измерений.

Статистический метод. В каждой точке рабочей зоны радионавигационной системы производится N измерений навигационных параметров, решается навигационная задача и вычисляется среднеквадратическое отклонение погрешности определения местоположении объекта. Недостатком метода является большое время и объем вычислений.

Метод косвенных измерений лишен недостатка предыдущего. В каждой точке рабочей зоны РНС определяются направляющие косинусов по следующим формулам на плоскости:

• - в пассивно-дальномерном режиме работы

  kx , =

  
  

  ky i =

  
  

  R бс,

  
  

Y - Y_Bc

1 БС

R бс ,

A = (kx,   ky ,), где Rбс, = (XX , - XБС )2 + (Y - УБС )2 - дальность от бортовой до i-ой опорной станции;

- в разносно- и суммарно-дальномерных режимах работы kx = X, XБС ± XВД XБС i R бс,        R вд

, = Y - YБС ± ^Д - YБС

R бс,      R вд

4 = (kx, ky ,), где RВД = V(XВД - XБС )2 + (УВД - Yc )2 - дальность от бортовой до ведущей станции, знак «+» для суммарно дальномерного, знак «-» для разностно-дальномерного режимов работы РНС;

- в квазидальномерном режиме работы kx =

Х _Б с- Xi

БС

R бс₁

, = X БС - X ,                   (8)

R бс , kt, = -1 A, = (kx , ky , kt,).

Далее вычисляется определитель матрицы^ по формуле

M = det ( A T A ) .                  (9)

Выбор наилучшего расположения опорных станций проводится по следующему алгоритму:

• 1)    формируется список комбинаций ОС общим числом сочетаний С^к _п = к!!(и!(к - и)!), где и - число опор-

• ных станций, к - число потенциальных мест размещения ОС;

• 2)    рабочая зона разбивается на исследуемые точки по оси А' на Nx, по оси У на Ny, в которых вычисляется значение Ми запоминается как элемент матрицы F . ., где z = 1...Nx,j= 1...Ny;

• 3)    если исследуется разностно- или суммарно-дальномерные режимы, то дополнительно организуется цикл v = l...k, когда одна из станций является ведущей;

• 4)    наилучшим вариантом комбинаций ОС (а также номер ведущей станции) считается тот, когда сумма элементов матрицы F дает минимальное значение.

Для проведения моделирования заданы координаты шести точек расположения опорных станций (таблица). Необходимо из возможных комбинаций ОС выбрать такие четыре, при которых геометрический фактор оказывает минимально-возможное влияние (рис. 1).

Точки опорных станций

№ ОС	X , м	У, м
1	1780852	19077
2	2143114	367945
3	2726775	26726
4	1740000	420000
5	1610000	270000
6	1800000	200000

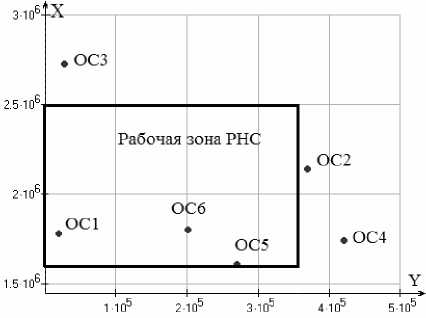
Рис. 1. Расположения опорных станций

В результате моделирования установлено, что наилучшим расположением обладают ОС с номерами в следующих режимах работы РНС: в пассивно-дальномерном -4, 3,2,1; в разносно-дальномерном-5, 3, 2,1 и ведущая станция 2; суммарно-дальномерном - 5,4,2,1 и ведущая станция 4; в квазидальномерном -5,3,2,1.

Результаты вычислений исследуемых режимов работы радионавигационной системы (поле теоретически рассчитанной погрешности координат) для станций с номерами 5, 3, 2, 1 и ведущая станция 2 приведены на рис. 2.

Как показывает моделирование, метод косвенных измерений по сравнению со статистическим более компактен и требует меньших вычислений. В силу этого рекомендуется применять данный метод для расчета теоретической погрешности в рабочей зоне РНС.

При работе радионавигационной системы квазидаль-номерный метод более предпочтителен, так как обладает погрешностью определения координат в рабочей зоне, сравнимой с полученной в дальномерном режиме работы РНС как в разносно- и суммарно-дальномерных режимах обеспечивает обслуживание бесконечного числа потребителей, а также дополнительно позволяет определять расхождение бортового и системного шкал времени, но за счет введения дополнительной третьей опорной станции.

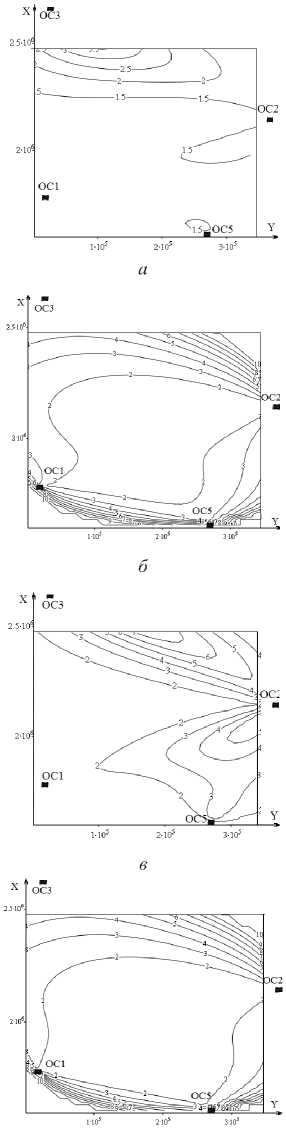
г

Рис. 2. Поле теоретически рассчитанной погрешности в четырех режимах работы РНС: а - дальномерном; б - разностно-дальномерном, в - суммарно-дальномерном;

г - квазидальномерном

В настоящее время для определения координат бортовой станции в радионавигационных системах ближней навигации (100-150 км) проводят измерения по формулам (2)-(5). В системах навигации средней дальности действия, измеренные дальности по сигналам радионавигационной системы и вычисленные в соответствии с выражением (2)-(5) будут отличаться друг от друга вследствие сферичности Земли. В настоящее время известно несколько способов решения данной проблемы. В работе [4] предложен способ перехода с плоскости на эллипсоид путем вычисления поправки, учитывающей сферичность Земли:

ar, = А"

'    6 R з ²

'( Y - Y ) ² + ( Y _ec - Y ) ² + ' _v + ( Y - Y o )( Y _E c - Y o ) ,

где У₀ - константа, равная 500 000 м, соответствующая смещению координат, используемому в системе Гаусса-Крюгера; R_З- радиус Земли в заданном регионе [2]; для перехода на эллипсоид поправку да необходимо отнять от R.

Другой способ определения дальности между двумя точками на эллипсоиде основан на решении обратной геодезической задачи (ОГЗ). Известно большое число методов решения ОГЗ, однако наиболее строгим является метод решения, основанный на алгоритме Бесселя. Данный метод обеспечивает точность не меньше 3-5 мм при любых расстояниях между точками, в том числе и в области высоких широт [4]. Метод Бесселя был приведен к виду для решения основных геодезических задач на любом эллипсоиде.

Недостатком данного способа является повышенная трудоемкость вычислений по сравнению со способом вычисления поправки за сферичность Земли. Однако при современном уровне вычислительной техники данный недостаток не является существенным.

Погрешность перехода с плоскости на эллипсоид с учетом поправки сферичности Земли можно определить по следующему алгоритму: задаются координаты двух точек на плоскости, и по ним вычисляются географические координаты, далее определяются расстояния на плоскости (R . ) и эллипсоиде (5.) по способу Бесселя, соответственно. Вычисляется поправка A R; и далее определяется погрешность перехода:

A, = S i -( R i -AR, ) . (11)

График погрешности перехода с плоскости на эллипсоид с учетом поправки за сферичность Земли в одной шестиградусной зоне в проекции Гаусса-Крюгера изображен на рис. 3.

Так, метод вычисления расстояния на плоскости с поправкой за счет сферичности Земли зависит от широты, и наибольшая погрешность достигает значения около метра на экваторе. Одна из проблем, встречающаяся при расчетах, - переход из одной зоны в другую в проекции Гаусса-Крюгера и определение расстояния между точками, находящимися в разных зонах проекции. При решении задачи в прямоугольной системе координат необходимо перейти к географическим координатам, задать требуемый меридиан и перейти обратно к прямоугольным, далее определить расстояние между двумя точками. При преобразовании координат растет мето дическая погрешность и увеличивается общее время вычислений.

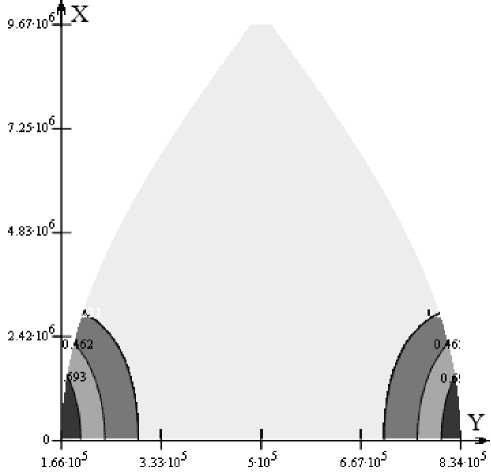
Рис. 3. Погрешность перехода с плоскости на эллипсоид в одной шестиградусной зоне

Для решения поставленной задачи разработан алгоритм определения координат на эллипсоиде, для уменьшения методической погрешности в географических координатах (широта, долгота) проведены исследования прямого и обратного преобразования координат географических в плоские на любом эллипсоиде [4]. Погрешность преобразования доведена до 10-4м на границе 6-градусной зоны за счет учета коэффициентов более высоких порядков.

Для решения навигационной задачи на эллипсоиде составляется система уравнений для определения координат, например, в квазидальномерном режиме, решение производится по итерационному методу Ньютона:

A₁₀ -A B + A 1,1 -A L + At- c = A R 1

A N ,0 -A B + A N,1 -A L + At- c = A R N

где A - матрица направляющих косинусов, элементы

Bn - B которой определяются как A 0 = —0

i,0

L - L

A j = —--- ^L Ne - cos ( B _o) ; A ₂ = -1 B_o , ^Lo - геодезичес-

• i,1          Si0

кие координаты начального приближения бортовой станции; A B, AL - поправки к координатам; В . , L- координаты опорных станций РНС; а - большая полуось эллипсоида, на котором заданы координаты станций РНС; е - эксцен-триситетэллипсоида; Ne = a ( 1 - e ²sin²( B 0 ) ) ² -радиус кривизны нормального сечения;

- 3

M = a ( 1 - e ² )( 1 - e ² sin² ( B 0 ) ) ² - радиус кривизны меридионального сечения; A R . = 5_ИЗМ . - 5 . - разность между измеренными и расчетными дальностями; R_ИЗMi. - измеренные дальности от БС до опорных станций; 5-расчет-ные дальности от объекта до опорных пунктов.

Система решается итерационным методом, состоящим в последовательном уточнении координат начального приближения^, L₀ [1]. Число итераций зависит от близости начального приближения к истинным координатам бортовой станции.

Алгоритм определения координат бортовой станции с учетом сферичности Земли для квазидальномерного режима работы РНС представлен на рис. 4. В результате моделирования получено, что число итераций не превышает 3-4 при точности вычислений, равной 1 мм.

Моделирование режимов работы РНС показывает, что предложенный алгоритм решения навигационной задачи на эллипсоиде обладает следующими достоинствами: получение несмещенных координат КС; высокая точность вычисления расстояний между двумя точками на эллипсоиде; вычисления производятся в географических координатах, в связи с чем устраняется ряд проблем, возникающих при определении координат в проекции Гаусса-Крюгера.

Итак, проведено исследование методов определения теоретической погрешности в рабочей зоне наземной радионавигационной системы. Метод косвенных измерений позволяет сократить на порядок время вычислений при сравнении со статистическим методом.

Разработан и исследован алгоритм определения наилучшего взаимного расположения станций в различных режимах работы и в рабочей зоне навигационной системы, который позволяет минимизировать влияние геометрического фактора расположения опорных станций на погрешность определения координат судна в рабочей зоне РНС.

Проработаны алгоритмы определения координат на плоскости и эллипсоиде в режимах работы радионавигационной системы: пассивно-дальномерный, разноснодальномерный, суммарно-дальномерный, квазидально-мерный. Исследования показывают, что квазидальномер-ный режим представляет собой наибольший интерес, так как обладает высокой точностью определения координат и большой зоной работы.

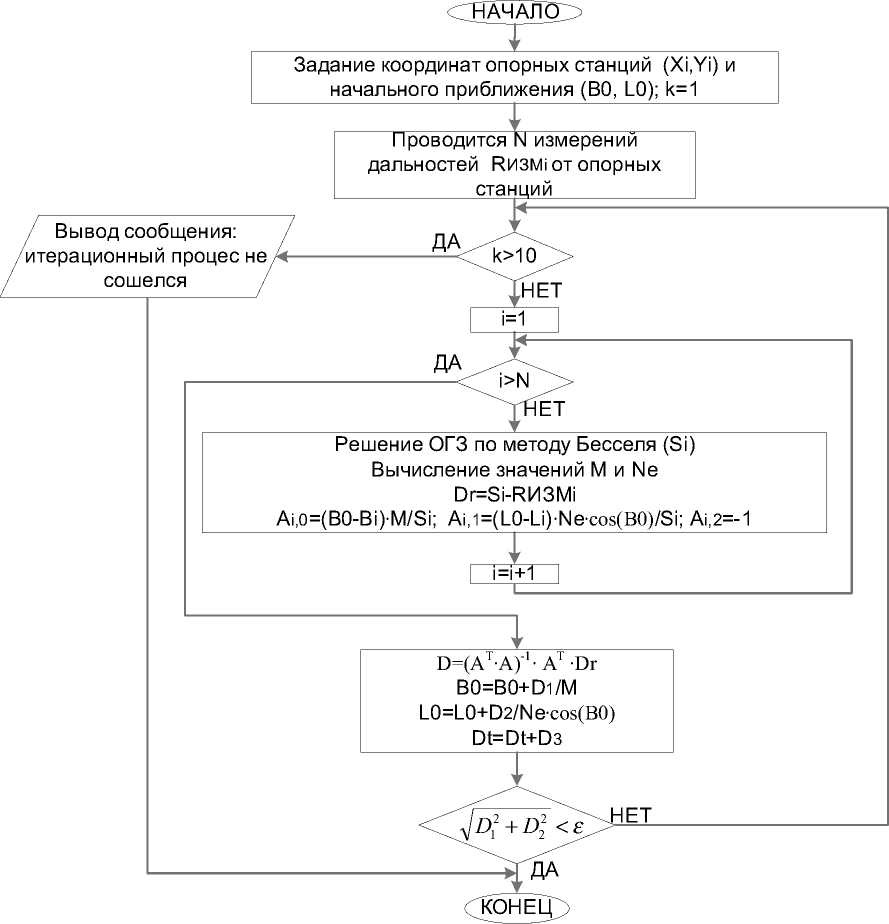
Рис. 4. Алгоритм определения координат бортовой станции в радионавигационной системе «Спрут»

Проведены исследования алгоритмов преобразования координат из прямоугольных в географические, предложены алгоритмы решения задач для любого эллипсоида, точность преобразований менее 10 4 м на границе 6-градусной зоны.

Проведены исследования алгоритмов вычисления основных геодезических задач на эллипсоиде, рекомендован метод Бесселя. Для уменьшения методической погрешности путем учета коэффициентов более высоких порядков, вычисление дальности доведено до 1-2 мм между двумя точками, находящихся на противоположенных сторонах эллипсоида, а также при решении задачи на любом эллипсоиде.

Разработан и рекомендован алгоритм определения местоположения на эллипсоиде через широту и долготу на базе итерационного метода Ньютона. В настоящее время разработанный алгоритм реализован в программном обеспечении вторичной обработки информации бортовой станции РНС «Спрут» с целью решения задач определения координат морских объектов.