Исследование погрешности разностного решения однонаправленного уравнения Гельмгольца методом вычислительного эксперимента

Высокая универсальность метода конечных разностей и связанные с ним широкие возможности для разработки параллельных вычислительных алгоритмов делает его эффективным средством решения многомерных краевых задач для дифференциальных уравнений, описывающих процессы распространения света в волноводах, что объясняет стабильный интерес исследователей к этой теме. При практическом применении метода конечных разностей важным является вопрос о фактической сходимости сеточных решений, получаемых с помощью разностной схемы, к решению исходной краевой задачи.

Численному решению краевых задач рассматриваемого класса, а также экспериментальной проверке сходимости разностных схем посвящён ряд работ [1 - 5 и др.]. Например, в работе [1] отмечено существенное влияние разрывности поля коэффициента преломления на скорость сходимости разностной схемы для уравнения Гельмгольца. В работах [2 -4] приведены результаты экспериментального исследования сходимости разностных схем для одно- и двумерных уравнений Гельмгольца с разрывным коэффициентом преломления, которые показали хорошее согласие экспериментальной скорости сходимости с теоретической. Однако следует отметить, что приведённые в этих работах результаты экспериментального исследования выполнены для весьма частных тестовых примеров, которые далеко не всегда могут быть формально «перенесены» на задачи с модификацией параметров, правых частей, начальных условий и т.п.

Настоящая работа посвящена экспериментальному исследованию методической погрешности конечно-разностного решения трёхмерного однонаправленного уравнения Гельмгольца, описывающего распространение электромагнитного излучения в волноводе прямоугольного сечения. Основное внимание уделено экспериментальному исследованию влияния на скорость сходимости сеточного решения таких параметров, как величина разрыва Δ n = n 1 - n 2

поля показателя преломления среды, а также величина параметра нелинейности среды ε _н / ε₀.

Проведение такого исследования потребовало применения весьма мелких сеток, что в случае трёх пространственных переменных сопряжено с большими объёмами вычислительных затрат и необходимой оперативной памяти. Для проведения расчётов были разработаны параллельные вычислительные алгоритмы, основанные на методе расщепления с использованием для решения разностных СЛАУ методов встречной и правой прогонок с циклическим разбиением области. Для решения нелинейной задачи использовалась процедура итерационного уточнения. Экспериментальные исследования сходимости производились с помощью суперкомпьютера «Сергей Королёв» в Самарском государственном аэрокосмическом университете.

1. Теоретические основы

Математическая модель

Рассмотрим обобщённое волновое уравнение для векторного поля электрической напряжённости [6]:

-v [ in ^ ] x[vx E i ]-v[v [ in s j - E i ]-

. ^p . d² E _n

-A E + su—— = 0, d t ²

где ц - магнитная проницаемость, Генри/м; E - напряжённость электрического поля, В/м; ε – диэлектрическая проницаемость, Фарад/м.

В случае учёта эффекта «самовоздействия» диэлектрическая проницаемость может быть представлена в следующем виде [7]:

^s = ^s _M ^+s z |E P| 2 ,

где ε _ср – среднее значение диэлектрической проницаемости, Фарад/м; ε _н – коэффициент изменения диэлектрической проницаемости под воздействием поля распространяющейся волны; | E | = I - интенсивность излучения, мкДж.

Будем использовать относительные величины магнитной проницаемости ц и диэлектрической проницаемости s :

2 i k у = ( k ² - k ² ) e -

2 я

X 0 ]

£ I -|2 . t l^El^{E -}0

-

ц = —= 1,(3)

Ц о

" nd + " LI   " nd   ";          "( ^-| ²

- =------= — + — I = s + — E .(4)

-0        -0    -0

-^д_т + -^д_т |E-v[v[ ln n ² ]-e] . д x ² д y ² J ^{L L ] ]}

В случае ТЕ-поляризации ( Ё ( x , y , z ) = ( 0, E y ,0 ) )

последнее уравнение представится в виде:

Также учтём, что при описании явлений для оптического (видимого, ультрафиолетового, инфракрасного) диапазона частот вместо относительной диэлектрической проницаемости рассматривается коэффициент преломления n =лП , который будем полагать функцией пространственной точки. Учитывая (2) – (4), запишем волновое уравнение в виде:

дЕ y _=J_ д z 2 k

+

2я

X 0 ]

+     |Ey +(k2 - k2 )Ey + дx   дy J x

- I |2

"г I^е y ^E y

^- 0

.

—

2 " । -|2 |       д2E n + E |-0Ц0 - 2

s ₀ J      д t

-v[v [ ln - ] - E ]-A E = 0,

где c = ----

Al ^- 0 ^Ц 0

– скорость света.

Далее при записи формул будем опускать индекс в записи Е _у , подразумевая под Е соответствующую компоненту вектора напряжённости электрического поля.

Математическая модель распространения электромагнитного излучения в волноводе прямоугольного сечения, ограниченном идеально проводящей оболочкой, будет иметь вид:

Для получения однонаправленного уравнения Гельмгольца используем замену вида:

®=_L ( k. - k ■)E + д z 2 k          ¹

д ди

—г +--г IЕ дx2 дy2 J

+

E ( x , y , z , t ) = E ( x , y , z ) exp [i ( to t + ф + kz ) ] ,     (6)

где ю = 2 л c / X ₀ - угловая частота; ф - начальная фаза; k = 2 п n / X ₀ - волновое число в заданной точке;

k = 2 п n / X ₀ - усреднённое значение волнового числа; λ₀ – длина волны в вакууме; n – среднее по пространственной области значение коэффициента преломления.

Далее будем предполагать:

n ( x ) = n + n ( x ) ,                                    (7)

где n ( x ) - малое уклонение от значения n .

Подставив (6) в уравнение (5), получим:

2 f 2    " н lyl2 ) p д 2 E

-to I n +— E |^ 0 ^Ц 0 Е ^-— y^-

(      S0 ^{1 1} )            ^д z²

- 2 i k — + k ²E- ^f^ + -^д_т Ъ -             (8)

д z        (д x ² д y ² J

-v[v[ In n ² ]-E ] = 0.

Сделаем предположение о «медленности изменения огибающей» вдоль оси z [6], т.е.:

in - _^

^X 0 n " 0

F ( E ) ,

” x e [0, l x ], y e [0, l y ], z e [0, l z ];

^El _z = ₀ =v ⁽ x , y), x ^{e [0,} l x ^], y ^{e [0,} l y ^];

E| x = 0 =^EI x = ix = ⁰, y e ( 0, l y ) , z e ( ^0, l z ];

_E| y = 0 =^EI y = ly = ⁰, x e ( ⁰, l x ) , z e ( ^0, l z ],

где l x , l y , l z – ширина, высота и длина волновода соответственно, мкм; F ( E ) = |E| ² E - функция «само-воздействия»; ψ ( x , y ) – напряжённость электрического поля на входе в волновод, В/м.

Разностная схема

Заменим область

Q = {0 < x < lx} x{0 < y < ly}x{0 < z < lz} непрерывного изменения аргументов для поля E(x, y, z) равномерной сеткой:

Q h ={ xl = ihx , i = 0, I }x{ y, = jhy , j = 0, J }x x{ zk = shz, s = 0, S}, д 2E дz2

« 2 k

дЕ д z

l            ly           l где hx = "у, hy = J, hz = "I

– шаги дискретизации.

В результате получим однонаправленное уравнение Гельмгольца, учитывающее эффект «самовоз-действия»:

Для численного решения нелинейной задачи (12)

используем следующую конечно-разностную схему с итерационным уточнением:

i m + 1

s

^U ij

0,5 h z

m + 1

+

⁸ fky ,_Z = Г⁽ °° S ⁺"^-E( x , y j , z s i ^, y j ^, s         _z

-

^+л hy °- + ( k j ^- k ² ) [ U s ⁺] ]+

^- 2 k [^Л x °° ^{S+ +Л} y ^E( x , y^{p z} s ^{) +}

in £ .

^X 0 n ^£ 0

F ( [ U s" ] ' ) • [ ^U j *4

^s ij ^,

+ ( k j -F ) 0 " ’i]-- ¹^ f ( t / " «) .

^{2 £} 0

m = 0, M ; i = 1, I - 1; j = 1, J - 1;

U s ⁺¹ - sj^{s +}J2 ij               ij

0,5 h z

= ЛГл, u s ^{+ 12} +л. u s ⁺¹ +

2 k [ hx j        hy j

+ (kj - k2)Uj+X] + ^F(Uj+%)• x                 J X0n £0 x '

j = I, J - 1; i = I, I - 1; s = 0, s - 1;

^U = 0 = ^v ( ^x-y j ) ^ i = ⁰- I ^   j = ⁰ J ;

U L = <, = ^:   » = ^s ^ j = J ;

^U j\, = 0 = ^U j\, = j = ^:    s = й ^ i = iT I - i^

Следует заметить, что функция F (E) не является дифференцируемой по комплексному аргументу E. Поэтому воспользуемся следующим представлением:

^{F ( 0} Г”Н ^F ( ^E+AE ) 1| x , y^-

= !|E + AE|2 x(E + AE)}|         = xi,yj,zs

где U_i^s_j – сеточная функция, взятая в узле ( i , j , s ),

= { [e| ² +|AE| ² + 2 ( Re E- Re AE +

+ Im E-Im AE)](E + AE)}|        = xi,yj,zs

= {|e| ² -e+|ae| ² -ae+|e| ² -ae+|ae| ² -e+

+ 2 ( Re E- Re AE + Im E- Im AE ) x

^л h U =

U i + 1 j - 2 U j + U^ j ^h x ²

U^{s s}                  '

^л hy ^U ij

-

ss

Z.L7 j + kJ j - 1 hy ²

– разностные операторы

Лапласа по переменным x и y соответственно; m –

x ( ^E + ^AE )l V _Z = ^F ( ^E ) + F z '( ^E ) h T + ^O ( h z ² ) .

x_i , y_j , z_s                        2

Далее, используя разложение функций, входящих в (17), кроме F ( UU S ⁺²²), по действительным переменным x , y , z и учитывая (18), получим:

номер итерации.

В случае линейного варианта задачи (12), т.е. если ε н = 0, необходимость в итерационном уточнении не возникает и схема (14) фактически совпадёт со схемой переменных направлений Писмена-Рекфорда [8].

Исследуем свойство аппроксимации схемы (14). Прежде всего, запишем выражение для вспомогательной сеточной функции U S ⁺²², которое нетрудно получить из первого и второго уравнений системы (14):

^U S ⁺* 8 h ^л hy U - '⁺¹ ]+ 2 ( ^u s + ^u s ⁺¹) • (15)

Подставив в (15) вместо сеточной функции U точное решение E( x , y , z ) задачи (12) и проведя разложение с помощью формулы Тейлора в окрестности точки ( x i , y j , z s ), получим:

⁸ f ' X V , x_i , y_j , z_s

= E' +E1

z

¹" hz zz ₂

E'" ^ h Z r zyy 4 k

■ E" -L ^xx 2 k

E”

zxx

i h Z

EL-1

4 k ^yy 2 k

^- 2 k ^{( k} j ^{- k 2 )x}

U^{s + 12} = ij

E + E‘ h z - + E'_z z ₂ zz

h 2     „ i h 2

-z --E” —J +

4      ^zyy 8 k

⁺ O ⁽ h, h z h y I.,-, = < ^E+AE ii x , y ,v i ^, y j ^, s                             ^{i j} s

где Ui⁺ - результат подстановки в (15) функции h

E ( x,y, z ) вместо U ; AE         =E_Z^- + O ( h_z ) .

x_i , y_j , z_{s         2}

Запишем невязку 8 f h для первого уравнения схемы (14) на точном решении краевой задачи (12):

h      h ²

xl E + E' - z - +E" - z- ( ^z 2 ^zz 4

^н F ( E ) -

2£0      x 7

^{1 kn} 0 ^£ н 2 £ 0

F Z ( E ) h z - + O ( h l, h z h y , h x , h y , h_z h x , h Z ) .

Продифференцируем первое уравнение системы (12) по переменной z :

2 2 Е = л[_{( k} ²- k ² ,^a . ^d . ^d )_E d z ² 2 k           ' d z ^5 x ²d z d y ²d z J

^{in £} н

^X 0 ^{n £} 0

F z '( ^E ) .

+

Если в выражении (19) учесть первое уравнение системы (12) и формулу (20), то будем иметь:

⁸ n\_{x v z} = O ( ^h 2 ^h² ) ^ i = 1^ I - 1^ x_i , y_j , z_{s                                               (21)}

j = 1, J - 1, k = 0, K - 1.

Невязки 8 f h = 0, S = 2,6, т.е. начальное и граничные условия разностной схемы, точно аппроксимируют исходные дифференциальные уравнения.

Таким образом, в случае линейной задачи в предположении достаточной гладкости решения погрешность аппроксимации схемы (14) будет квадратичной по всем шагам дискретизации. Для нелинейной задачи квадратичность погрешности аппроксимации будет иметь место в случае сходимости итерационного процесса при m → ∞.

На рис. 1-2 представлены графики интенсивности комплекснозначной амплитуды, полученные с помощью разработанной схемы (14), а также рассчитанные по формуле (26). Расчёты проводились при следующих значениях параметров: λ = 0,63 мкм, l_x = 10 мкм, l_y = 10 мкм, l_z = 6 мкм, n = 3,6, I = 32, J= 32, S = 300.

2. Экспериментальное исследование сходимости Линейное уравнение Гельмгольца с постоянными коэффициентами

Пусть U _{hx , hy , hz} – численное решение схемы (14), полученное на сетке с шагами дискретизации h_x , h_y , h_z . Если решение E ( x, y, z ) задачи (12) достаточно гладкое и имеет место (21), а также если схема (14) устойчива, то для погрешности метода сеток можно записать:

6 = a h +в h y +Y h Z + O ( h Z , h_zh Z , h_zh y ) ,         (22)

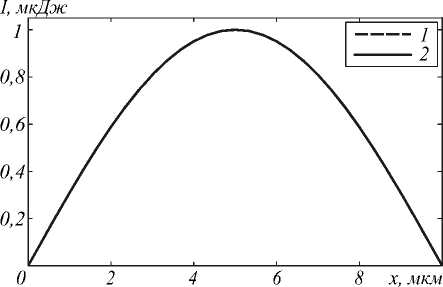
Риc. 1. Распределение интенсивности вдоль оси Ox при y = 5 мкм, z = 6 мкм, полученное аналитически (кривая 1) и с помощью схемы (кривая 2)

где 6 - погрешность численного решения U\h h h .

Если взять более мелкую сетку, например с шагами дискретизации h_x = h x / 2, h y = h y / 2, h_z = h z / 2, и рассчитать решение U l hxhy h _L, то погрешность 6 ₂,₂,₂

будет иметь вид:

Г h 12 Г К 12 Г h 12

^{6 =} 4 l x ] ^{+ P}[ "2J ^+Y[ J ⁺

+ O

h z

V

hz

—

h 1 ²

hz

—

h y

2I

Очевидно, что погрешности £ и 6 будут связаны

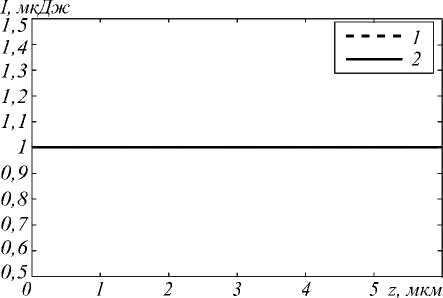
Рис. 2. Распределение интенсивности вдоль оси Oz при x = 5 мкм, y = 5 мкм, полученное аналитически (кривая 1) и с помощью схемы (кривая2)

соотношением:

о 1

⁶= 4 ⁶ -

Таким образом, следует ожидать уменьшения погрешности численного решения приблизительно в четыре раза.

Рассмотрим следующее начальное условие:

Как видно из графиков, численное и аналитическое решения совпадают с высокой степенью точности, при этом мода сохраняет свой вид на рассмот-

I П I v ( x , y ) = Sin     x Sin

V lx 7

(_ Л

П

r y

V y 7

.

ренном участке волновода, что хорошо согласуется с теорией [9].

Проведём исследование скорости сходимости конечно-разностной схемы (14), меняя шаги соглас-

Оно является гладким и представляет собой собственные функции оператора Лапласа. В этом случае краевая задача (12) при постоянном коэффициенте преломления и при отсутствии эффекта «самовоз-действия» (т.е. ε _н = 0) имеет следующее аналитиче-

но вышеописанному методу, и проследим за величиной погрешности в равномерной:

6 a =

_ max     |e(x.,y ,zs)| -|U"Г i=0,I; J-=0, J; s =0,sl A 1 jl M I ij I

__max      E( x,., y, zs )| i=0,I; J=0, J; s=0,s         1 J s

ское решение:

E ( x , У , z ) = exp

i

2 kn

G A²

I-I

V ix 7

V

x

и среднеквадратической нормах:

. In I .

X Sin x Sin

V ix 7

n

r y

V y

E_.

ñê

zzz

_ | i = 0, 1 J = 0, J s = 0, s

|^{e( x} i , y j ,^z s )|^{2 -}M

I • J • s

iax        E ( x ,., y , z_s )|

=0, J ; s = 0, S              j ^S

max

i = 0, I ; J = 0, J ; s = 0, S’

12 ₁ 2

.

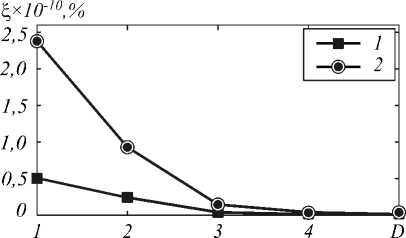
На рис. 3 представлен график зависимости погрешности численного решения от номера сетки D (количества интервалов разбиения). Соответствующие значения погрешностей приведены в табл. 1. Расчёт проводился при следующих значениях параметров: λ = 0,63 мкм, l_x = 10 мкм, l_y = 10 мкм, l_z = 2000 мкм, n = 3,6, S = 300.

Тогда

U ij l hxhyhz =^E ( ^X i , y j , ^z s ) ^{+ a}

2,2,2

h

+Y7

+ O

h x I ² 2

+e

h y T

+

V

hi 1

hz

----------•

i = 0, I , j = 0, J , s = 0, s .

h . 1²

hz

, ₂

•

h y

В качестве характеристики погрешности численного решения возьмём следующую величину:

n =

^U\_h.h,^_z - Uk , hL , hz

^U hx hy hz _р

41 К-Д, ⁽“ h

+

+ в h y +Y h Z + O ( h z , h z h y , h z h x ) .

Очевидно что для сетки в 2 раза более мелкой будем иметь:

Рис. 3. Графики погрешностей в среднеквадратической (кривая 1) и равномерной (кривая 2) нормах

Таблица 1. Значения погрешностей

ξ ск ×10-10, %	ξ р ×10-10, %	D	S×I×J
0,5060	2,3800	1	3×3 ×3
0,2390	0,9280	2	6×6 ×6
0,0376	0,1440	3	12×12 ×12
0,0102	0,0377	4	24×24 ×24
0,0028	0,0111	5	48×48 ×48

/X

n =

U\hXL hL hz. ^- U l hx hy hz 2 2 2        4 4 4

U hx hy hz

2 2 2 р

Из таблицы 1 видно, что как в среднеквадратической, так и в равномерной норме скорость сходимости численного решения к точному близка к квадратичной. Стоит отметить, что погрешность сеточного решения близка к машинному нулю, что свидетельствует о высокой точности этого решения.

Линейное уравнение Гельмгольца с пространственным распределением коэффициента преломления

Рассмотрим случай, когда коэффициент прелом-

ления среды зависит от пространственных переменных и представляет собой ступенчатую функцию:

n1, n (xЙ n 2,

— + b <  x < — - b ;

— - b <  x < — + b , 22

где b – ширина, а Δ n = n ₁ - n ₂ – высота ступеньки.

В данном случае проблематично получить аналитическое решение задачи (12). Следовательно,

+в h y +Y h z + O ( h z , h z h y , h z h x ) .

Таким образом, следует ожидать выполнения приближённого соотношения:

n « (V4) n .                                    (34)

Вычисление погрешностей n и т) проводится по значениям сеточного решения на двух сетках, одна из которых вдвое мельче другой. При этом разность значений сеточной функции вычисляется в узлах крупной сетки.

Проведём исследование скорости сходимости схемы (14) на тестовых примерах для двух случаев, различающихся высотой ступени Δ n . Подадим на вход волновода собственные функции оператора Лапласа (27) и рассчитаем решение на сетках различной мелкости. На рис. 4-5 приведены графики зависимости погрешности численного решения от номера сетки, рассчитанные при следующих параметрах: λ = 0,63 мкм, n 1 = 3,6, b = 2 мкм, l x = 10 мкм, l_y = 10 мкм, l_z = 6 мкм.

Соответствующие значения погрешностей приведены в табл. 2 и 3.

вычислить погрешность сеточного решения так же, как это было и в предыдущем случае, не представляется возможным. Поэтому для получения инфор-

мации о скорости сходимости численного метода поступим следующим образом. Запишем соотноше-

ние, связывающее точное и сеточное решения, предполагая сходимость последнего квадратичной:

U s L „ „ =^E ( x ^, y j , z s ) ^+a h x ^+e h ⁺y h z ⁺ x ^, y ^, z

+ O ( h , h z h , hh X ) , i = 0, I , j = 0, J , s = 0, s .

Таблица 2. Значения погрешностей, n2=3,58

η ск ×10-3, %	η р , %	D	S×I×J
8,6437	5,1646	1	60×8 ×6
4,4839	6,3085	2	120×16 ×12
1,7268	9,5504	3	240×32×24
0,2662	3,2471	4	480×64 ×48
0,0437	1,6857	5	960×128 ×96
0,0079	0,8926	6	1920×256 ×192
0,0015	0,4460	7	3840×512 ×484
0,0003	0,2247	8	7680×1024 ×768

Таблица 3. Значения погрешностей, n2=3,5

η ск ×10-3, %	η р , %	D	S×I×J
6,4882	9,7011	4	480×64 ×48
4,1272	7,1334	5	960×128 ×96
2,3142	5,7083	6	1920×256 ×192
1,1735	3,7718	7	3840×512 ×484
0,5758	2,5396	8	7680×1024 ×768

сетки. Стоит отметить, что в случае n 2 = 3,58 использование сеток более высокой мелкости, чем сетка 4000 × 150 × 20, уже не даёт каких-либо визуальных изменений численного решения, в то время как в случае n ₂ = 3,5 визуальные изменения решения значительны, хотя неуклонно уменьшаются.

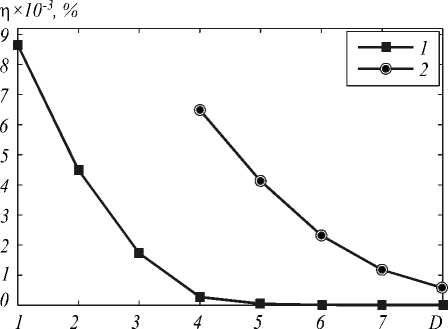
Рис. 4. Графики погрешностей в среднеквадратической норме при n2=3,58 (кривая 1) и n2=3,5 (кривая 2)

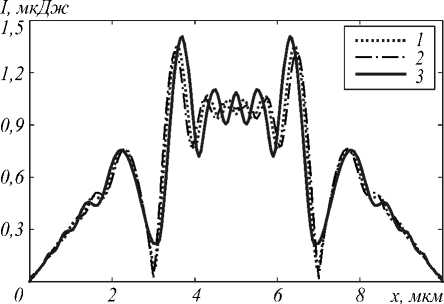
Рис. 6. Численное решение при n2 = 3,5, y = 5 мкм, z = 6 мкм, полученное на сетке: 2000 × 150 × 20 отсчётов (кривая 1), 1000 × 100 × 10 отсчётов (кривая 2), 6000 × 200 × 30 отсчётов (кривая 3)

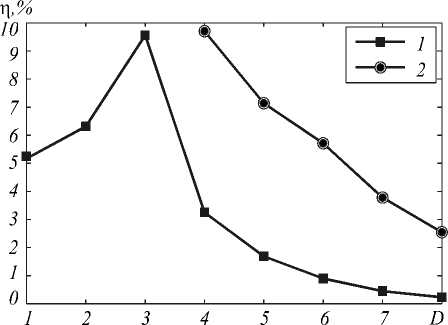
Рис. 5. Графики погрешностей в равномерной норме при n2=3,58 (кривая 1) и n2=3,5 (кривая 2)

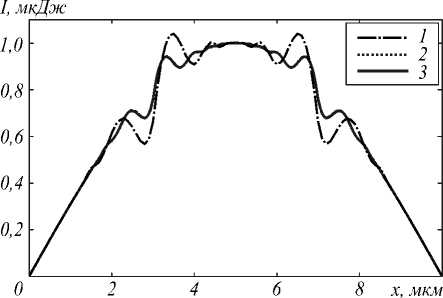
Рис. 7. Численное решение при n2 = 3,58, y = 5 мкм, z = 6 мкм, полученное на сетке: 2000 × 150 × 20 отсчётов (кривая 1), 1000 × 100 × 10 отсчётов (кривая 2), 6000 × 200 × 30 отсчётов (кривая 3)

Анализируя полученные результаты, можно сделать вывод, что сеточное решение конечно-разностной схемы (14) сходится.

Однако скорость сходимости сильно зависит от высоты ступени коэффициента преломления. Так, в случае n 2 = 3,58 скорость сходимости близка к квадратичной в среднеквадратической норме, а в случае n 2 = 3,5 она на порядок ниже. В равномерной норме в обоих случаях сходимость близка к линейной, хотя для случая с большим разрывом в коэффициенте преломления схема сходится значительно медленнее.

Результаты моделирования, представленные на рис. 6 - 7, были рассчитаны на следующих параметрах: λ = 0,63 мкм, l x = 10 мкм, l y = 10 мкм, l z = 6 мкм, n 1 = 3,6.

Из графиков видно, что чем сильнее разрыв в коэффициенте преломления, тем сильнее осцилляции сеточного решения в окрестности точки разрыва, которые медленно стабилизируются с измельчением

Нелинейное уравнение Гельмгольца с учётом эффекта самовоздействия

Поскольку на данный момент решение краевой задачи для нелинейного однонаправленного уравнения Гельмгольца не получено, для исследования погрешности и скорости сходимости схемы (14) применим ту же технологию, что и для линейной задачи со ступенчатым коэффициентом преломления.

Подадим на вход волновода гауссов пучок:

v ( x , y ) = P 2 exp n a

^^^^^^»

2 .   21

x+ y a2

.

Результаты численного моделирования представлены на рис. 8 - 9. Расчёты производились при следующих значениях параметров: n₁ = 3,6, λ = 0,63 мкм, l_x = 10 мкм, l_y = 10 мкм, l_z = 6 мкм, I = 30, J = 30, S = 4000, m = 5, ε н / ε 0 = 0,5.

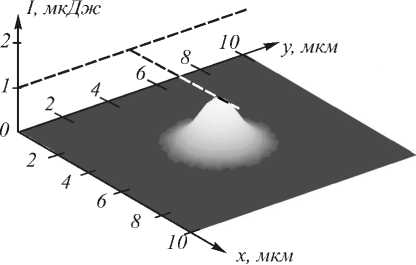
Рис. 8. Распределение на входе в волновод

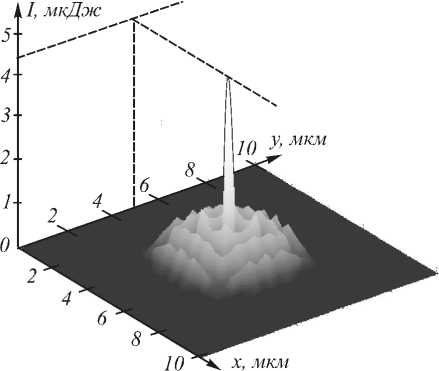
Рис. 9. Эффект фокусировки в точке z = 6 мкм

Численное моделирование процесса распространения электромагнитной волны в нелинейной среде, проведённое с помощью разработанной разностной схемы, позволило наблюдать на вышеприведённом графике явление самофокусировки излучения (т.е. смещения энергии излучения к центру пучка), что вполне согласуется с теорией электромагнитного излучения [10]. Однако на рис. 9 наблюдаются ложные пики, которые исчезают с дальнейшим измельчением сетки. На рис. 10 приведён график установившегося поля решения, полученного в процессе измельчения сеток. Расчёты были проведены при следующих значениях параметров: n1 = 3,6, λ=0,63 мкм, lx = 10 мкм, ly = 10 мкм, lz = 6 мкм, I = 100, J = 100, S = 6000, m = 5, εн /ε0=0,5.

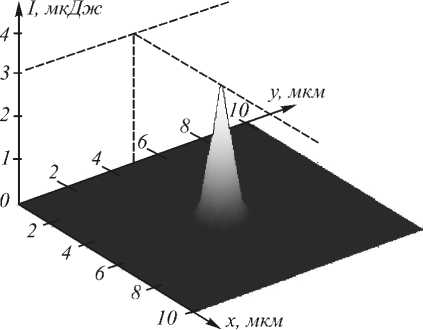
Рис. 10. Эффект фокусировки в точке z = 6 мкм

На рис. 11 и в табл. 4 приведены результаты исследования погрешности численного решения и скорости сходимости схемы (14).

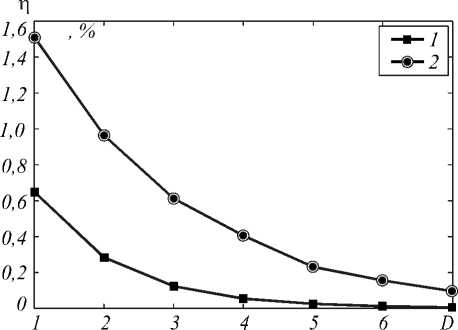
Рис. 11. Графики погрешностей в среднеквадратической (кривая 1) и равномерной (кривая 2) нормах

Таблица 4. Значения погрешностей

η ск , %	η р , %	D	S×I×J
0,6474	1,5081	1	128×8 ×8
0,2832	0,9631	2	256×16 ×16
0,1236	0,6116	3	512×32×32
0,0544	0,4054	4	1024×64 ×64
0,0255	0,2317	5	2048×128 ×128
0,0118	0,1562	6	4096×256 ×256
0,0056	0,0957	7	8192×512 ×512

Анализируя полученные результаты, легко заметить явление сходимости разностной схемы. Однако скорость сходимости не совпадает с теоретической, т. е. не является квадратичной и близка к линейной. Попытки увеличить количество итераций уточнения не привели к улучшению сходимости. Так, к примеру, различие сеточных решений для m =4 и m =5 характеризуется величиной 10^-7 % и быстро убывает на следующих итерациях.

Приведённые результаты потребовали проведения расчётов на весьма мелких сетках. Эти вычисления были выполнены с использованием разработанных параллельных алгоритмов и привлечением высокопроизводительной техники.

• 3.    Параллельные алгоритмы

Вследствие огромной трудоёмкости (десятки миллиардов и более вычислительных операций) для решения задачи были разработаны параллельные алгоритмы расчёта. Первый алгоритм основан на решении СЛАУ методом встречных прогонок с циклическим разбиением, второй – на решении СЛАУ методом правой прогонки с циклическим разбиением области [11, 12]. Для учёта зависимости правой части от решения на предыдущем слое, в которой задействован разностный оператор Лапласа, необходимо разбивать расчётную область на участки с перекрытием в три узла, что является особенностью разработанных алгоритмов.

Приведём результаты исследований для нелинейной задачи. При решении данной задачи применяется итерационное уточнение. В процессе расчёта на вход волновода подавались собственные функции оператора Лапласа (25) и использовались следующие значения параметров: n ₁ = 3,6, λ=0,63 мкм, l_x = 10 мкм, l_y = 10 мкм, l_z =6 мкм, m = 5, ε _н /ε₀=0,5.

На рис. 12 представлено ускорение T_алг , полученное за счёт применения параллельных алгоритмов. Расчёты производились на суперкомпьютере с использованием сеток, указанных в табл. 5.

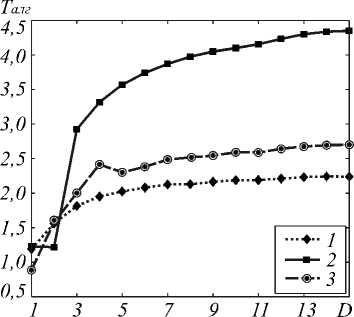
Рис. 12. Ускорение параллельных алгоритмов: правой прогонки на двух процессорах (кривая 1), правой прогонки на четырёх процессорах (кривая 2), встречных прогонок на четырёх процессорах (кривая 3)

Таблица 5. Размеры сеток

D	S×I×J	D	S×I×J
1	100×10 ×10	9	1700×160 ×160
2	250×20 ×20	10	1900×180 ×180
3	450×40×40	11	2100×200 ×200
4	650×60 ×60	12	2500×240×240
5	850×100×100	13	2900×280 ×280
6	1100×120×120	14	3300×320 ×320
7	1300×140×140	15	3700×360 ×360
8	1500×160×160	16	4100×400 ×400

Из графиков видно, что наилучший результат показал алгоритм правой прогонки для четырёх процессоров, достигнув ожидаемого ускорения в четыре раза. Несколько отстаёт от него алгоритм встречных прогонок.

На рис. 13 представлено ускорение T тех , которое определяется как отношение времени работы программы на персональном компьютере ко времени работы программы на суперкомпьютере для соответствующих реализаций последовательного и параллельных алгоритмов.

Легко видеть, что суперкомпьютер в разы быстрее производит вычисления. В случае решения нелинейной задачи с итерационным уточнением применение последовательного алгоритма даёт ускорение примерно в 32 раза по сравнению с ПК. В случае применения параллельных алгоритмов наблюдается падение ускорения в направлении от крупных сеток к мелким, однако оно остаётся весь- ма значительным (не менее, чем в 18 раз). Различия в ускорениях для алгоритмов распараллеливания на четыре и два процессора объясняется конфигурацией ПК (на основе Intel(R) Core(TM) 2 Duo CPU, 2 Гб оперативной памяти). Следует отметить, что решение такой задачи на ПК с использованием сеток мельче, чем 1100 × 120 × 120 отсчётов, является проблематичным вследствие нехватки оперативной памяти.

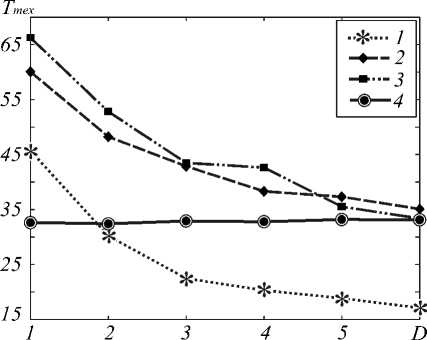
Рис. 13. Ускорение, полученное за счёт использования суперкомпьютера «Сергей Королёв», для алгоритмов: правой прогонки на двух процессорах (кривая 1), правой прогонки на четырёх процессорах (кривая 2), встречных прогонок на четырёх процессорах (кривая 3), последовательного на одном процессоре (кривая 4)

Заключение

Получены следующие результаты:

• 1.    Экспериментально подтверждена сходимость схемы (14) для рассмотренных тестовых примеров. При этом для случая линейной краевой задачи (12) с постоянными коэффициентами, т.е. при отсутствии эффекта «самовоздействия» (ε _н = 0) и постоянстве коэффициента преломления, скорость сходимости оказалась близка к квадратичной как в равномерной, так и в среднеквадратической норме, что вполне согласуется с результатами теоретического исследования.

• 2.    Установлено, что в случае пространственной зависимости коэффициента преломления, описываемого разрывной функцией (29), скорость сходимости существенно зависит от величины разрыва Δ n = n ₁ – n ₂. Так, с ростом Δ n эта скорость в среднеквадратической норме фактически падает на порядок: от квадратичной до линейной.

• 3.    При решении нелинейной задачи, учитывающей эффект «самовоздействия» (ε н /ε 0 =0,5), скорость сходимости схемы (14) оказалась близка к линейной. Увеличение количества шагов m итерационного уточнения не позволило существенно повысить скорость сходимости схемы.

• 4.    Использование специальных параллельных алгоритмов и высокопроизводительной техники позволило существенно (в 18 - 67 раз) уменьшить время расчётов для решения рассматри-

• ваемой задачи, а также одновременно повысить на один-два порядка точность искомого решения за счёт измельчения сетки, задействовав при этом несущественную часть всех мощностей суперкомпьютера.

Работа выполнена при поддержке ФЦП «Научные и научно-педагогические кадры инновационной России» (госконтракт № 14.740.11.0016), грантов Президента РФ поддержки ведущих научных школ (НШ-4128.2012.9) и молодого кандидата наук (МК-3912.2012.2), и гранта РФФИ (12-07-00269).