Исследование поля и энергии в слабопроводящем оптоволокне со степенным профилем показателя преломления произвольной степени

В качестве оптических волокон применяются диэлектрики со ступенчатым или градиентным профилем показателя преломления. Ведутся интенсивные экспериментальные исследования по поиску оптимальных материалов волокон для тех или иных целей. Аналитически

Technologies, machinery and equipment исследованы волноводы для волокон со ступенчатым профилем показателя преломления. С градиентным профилем показателя преломления аналитика осложняется в связи с трудностями при решении достаточно сложных уравнений, возникающих из-за пространственной зависимости профиля

показателя преломления. Эксперименты показали, что хорошей моделью для математического исследования физических процессов с градиентным профилем может служить модель степенного профиля показателя преломления. Самое известное точное решение связано с неограниченным параболическим профилем показателя преломления. В связи со сложностями при получении точного решения для других случаев градиентных профилей разрабатываются разнообразные приближенные методы решения таких уравнений.

Целью настоящей работы является приближенное решение для поля в сердцевине слабопроводящего градиентного световода (в одномодовом режиме) в случае степенного (в общем виде) профиля показателя преломления и исследование зависимости энергии поля в сердцевине волновода от волноводного параметра.

Обзор литературы

В науке и технике давно используются оптические волокна (световоды), по которым могут распространяться оптические лучи. Достаточно полные и общие сведения о световодах и диэлектрических волноводах содержатся в фундаментальной монографии А. Снайдера и Дж. Лава, где широко представлена информация о различных видах волноводов с кратким описанием экспериментальных и теоретических результатов с большим количеством примеров и различных математических методов1. Однако со времени издания этого труда прошло немало времени, и исследования по этой тематике значительно продвинулись. Кратко отметим их направления.

Предложено устойчивое к изгибам одномодовое волокно с большой площадью моды и низкими потерями на изгибе [1]; дан анализ многожильного маломодового волокна с составным профилем показателя преломления и двойной вспомогательной структурой [2]; смоделирована и вычислена уникальная трехмерная прерывистая конечно-элементная модель Петрова – Галеркина для моделирования лазерного усиления в волоконном усилителе [3]; предложены оптоволоконные датчики, основанные на френелевском отражении на конце волокна [4]. Усовершенствован и модифицирован метод расширенной тангенс-функции (применяется для получения оптических солитонов для двухъядерных ответвителей кубической четверти (CQ) в оптических метаматериалах, имеющих секстический степенной закон Кудряшова с произвольным показателем преломления) [5]; рассмотрены ребристые волноводы, в которых направляющий слой в основном состоит из пластины с наложенной на нее одной или несколькими полосами [6]; исследованы сегментированные волноводы (такие волноводы могут периодически изменять свое поперечное сечение, обеспечивая передачу света без потерь через так называемые блохов-ские моды) [7].

Заслуживает внимание работа, где впервые были предложены перспективные микроструктурированные или дырчатые волоконные световоды из кварцевого стекла. В оболочке таких световодов делаются продольные отверстия, расположенные в поперечном сечении относительно друг друга в том или ином порядке [8]. Большой контраст показателя преломления сердцевины и оболочки определяет уникальные оптические свойства таких волноводов. В частности, варьируя геометрию оболочки, можно управлять дисперсионными свойствами световода. Математический аппарат для анализа таких световодов можно найти в других статьях [9–11]. Возможность управления показателем преломления оболочки в таких волноводах позволяет создавать одномодовое оптоволокно. В нем на любой длине волны распространяется только одна мода (еще одна особенность таких волноводов – существование одномодового режима в волокнах с большим диаметром сердцевины). Различные аспекты этого направления хорошо представлены [12–15].

Что касается классических градиентных световодов, то на сегодняшний день получено точное решение для поля в волокне только в случае неограниченного параболического профиля: обобщенные полиномы Лагерра в цилиндрических координатах или функции Гаусса – Эрмита в декартовых. Подробный анализ этого решения можно найти в классической литерату-ре2. Для произвольного градиентного планарного волновода получены модовые решения уравнения Гельмгольца – амплитуда моды представлена в виде экспоненты с показателем в виде ряда Тейлора, коэффициенты которого находятся из рекуррентных соотношений [16]. С помощью моделирования показано, что градиентные микролинзы Микаэляна и «рыбий глаз» Максвелла могут формировать изображения со сверхразрешением.

Представлен новый подход к разработке структурированных оптических волокон. Показано, что при внутреннем наноструктурировании сердцевины, состоящей из двух стекол, могут быть созданы волокна с эффективным профилем градиента показателя преломления с заданным распределением показателя преломления [17].

В случае трехмерного градиентного световода с круглым поперечным сечением ранее нами получено в первом приближении аналитическое выражение для поля и энергии в одномодовом режиме внутри слабопроводящего волокна со степенным профилем показателя преломления с произвольной степенью (с учетом поляризации) путем решения уравнения Гельмгольца методом функции Грина. Построены зависимости энергии от волноводного параметра для второй и третьей степени профиля показателя преломления выражения. Показано, что в рассматриваемом приближении энергия увеличивается с ростом волноводного параметра до определенного значения параметра, после которого зависимости энергии от волноводного параметра меняются местами для второй и третьей степени [18].

В настоящей работе другими методами, отличными от примененных в статье [18], мы определим поле и энергию в одномодовом режиме внутри слабопроводящего волокна со степенным профилем показателя преломления с произвольной степенью без учета поляризации (что упрощает вычисления), построим соответствующие зависимости энергии и результаты сопоставим с результатами предыдущей работы [18]. Тем самым мы полностью решим задачу без учета поляризации и с учетом поляризации. Результаты данной и предыдущей [18] работ могут быть использованы для конструирования световодов в зависимости от конкретных приложений (в частности, построенные зависимости энергии от волноводного числа могут помочь подобрать материал сердцевины световода с подходящей степенной зависимостью профиля показателя преломления).

Материалы и методы

Выведем уравнение для поля в световоде с градиентным профилем показателя преломления. Пусть

{ e ( t , R ) , h i ( t , R ) }

соответственно элек-

трическая и магнитная составляющие

n ² ( r ) =

₍ n Co [ 1 - ^{2 A h} ( r ) ] ^,0 ^ r ^ P ,

электромагнитного поля ( t – время, R = ( x , y , z ) - координаты). Из уравне-

ний Максвелла для диэлектрических сред с показателем преломления n 2 ( R ),

2 A =

nd, r > P, ndcA h(0) 0, nt   ’ h ( p )=1,

отделяя временную часть, в результате преобразований для электрической компоненты электромагнитного поля (для магнитной компоненты аналогично) получим:

e ( t, R ) = E i ( R ) exp ( - i m t ) ^ A E + k ² n ² E i =

= -V ( E, V [ ln( n ²) ] ) ,           (1)

где c – скорость света, ω – циклическая частота, k = w / с. Для волокна (сердцевины) градиентного световода n ² = = n ²( r ), r = 4x 2 ⁺ У ², поле в волокне также зависит от r и распространяется вдоль оси z . Для поля E запишем ( и_z , р, ф - соответственно единичный вектор направления распространения поля вдоль оси z , постоянная распространения и угол в плоскости ( x , y ))

E i ( R ) = n_z exp ( i p z ) exp ( im ф ) E ( r ) . (2)

Случай с ненулевой правой частью в (2) в первом приближении рассмотрен нами в другой работе [18]. Отбрасывая в (1) правую часть (не рассматривая поляризационные свойства, описываемые членами, содержащими v { ln n ² } ), от (1), (2) перейдем к скалярному уравнению в полярных координатах для основной моды ( m = 0):

d ² E ( r ) 1 dE ( r ) dr ² r dr

+ ( k ² n ² ( r ) - P ² } E ( r ) = 0. (3)

Показатель преломления для волновода обычно записывается в следующем виде:

где h ( r ) - возрастающая от 0 до 1 функция при изменении r от 0 до р ; n o , n^ -показатели преломления волокна и оболочки; Δ – высота профиля; ρ – радиус круглого в поперечнике волокна.

Подставляя (4) в (3), запишем результат в виде (перейдем к безразмерной переменной у )

^d-^ ₊ ¹ E j ^ ¹ ₊ ( Z . P ) ’ E ( _Y ) = d y    у d y

= V ² h ( у ) E ( у ) ;

у = r/ p , Z i ^{2 =} k² n Co - P

V = k p NA, NA = 7 n Co - n 2 ,   (5)

здесь V , NA – волноводный параметр и числовая апертура.

При этом (4) принимает вид n 2 ( / ) =

;n2co [1 - 2Ah (у )], 0 < у < 1, nd, У > 1,

7A ₌ n™ ^- n C ^{h ( 0 )} 0, "  n_c ² _o ’ h ( 1 ) 1.         (6)

Результаты исследования

Найдем решение уравнения для поля в световоде с градиентным профилем показателя преломления.

Поскольку d2 Eо (У) , 1Eо (У) dy2           '

+ ( Z i p ) ² E о ( У ) = ⁰ ^

у d y

^ E 0 ( У ) = J 0 ( Z i py ) ,        (7)

то решение уравнения (5) будем искать в виде

E ( Y ) - f ( Y ) E о ( Y ) .        (8)

Подставляя (8) в (5), с учетом (7) для неизвестной функции fу) получим уравнение л7)+(7+2 Ei) f'(7 )-

- V ² h ( 7 ). f ( 7 ) = о, f ГЧ 7 )- ^ Ь)

Заменим здесь функцию Бесселя E о ( Y ) = J о ( X i PY ) , описывающую одномодовый режим волновода со ступенчатым профилем, на гауссову функцию ( r 0 - радиус модового пятна):

Eо (y)=Jо (Xi PY ) ^ Eo (y) =exp\-ay2 / 2}, а = P2/ro2,             (10)

причем (см. [18–22]):

Рассмотрим коэффициент при первой производной и выясним, при каких значениях у он обращается в нуль (воспользуемся (11)):

- 2 ау = 0 ^ у

Y

4ъх

V 0,32

e{F е(0;2,4)}е(0,74; 3,54), откуда

->2 ау ^ у < 0,74, -<2 ау ^ у > 3,54. (13) у                у

Выбирая первый вариант для поля внутри сердцевины волновода, перепишем (12) в упрощенном виде f " (Y) +1 f' (Y)-V2h(Y) f (Y) = 0, Y

( y <  0,74 ) .                (14)

0,4 X r^{0 =} NA

> а =    = 0,16 V ²;

r 0 ²

V е ( 0; 2,405 )

(NA = х / n2 - nг,, co cl , to 2л )

V = k p NA , k =  =    ,    (11)

c X )

Решать уравнение будем аналогично методу ВКБ (Вентцеля – Крамерса – Бриллюэна)3 (современное изложение в [23]).

Итак, искомую функцию запишем в виде

.^f ( Y ) = ^exP { P ( Y ) } ^

^ ^f / ( Y ) = P / ( Y ) ^f ( Y ) ,     ⁽¹⁵⁾

обоснование применения этой формулы для нашего случая, полученной для волновода со ступенчатым профилем показателя преломления, показано в другой работе [21]. Подставляя (10) в (9), запишем уравнение в виде f " (т) + f1"2ат^f' (т)“

I т J

• - V ² h ( т ) f ( т ) - 0.      (12)

^f " ( Y ) = P " ( Y ) ^f ( Y ) + ( P / ( Y ) ) ^{2 f} ( Y ) .

Подставляя в (14), получаем уравнение для функции p (γ)

Р " ( Y ) + { P / ( Y ) } ² +

+ — p ² ( y )^_ V²h ( Y ) ⁼ 0.       (16)

Y

Предположим малость второй производной p // ( у ) :

I p " ( г )|«|- V²h ( г )| = V²h ( г ) . ⁽¹⁷⁾

Тогда для (16) мы можем записать

Р ' ( Y ) = У ( Y ) ^ У ² ( Y ) + 1У ( Y )^- V²h ( Y ) ^ 4 P ' ( 7 ) }_u = ( У ( 7 ) }„ =

₌ _ _ L + _ L ^ 1 + 4 V 2 h ^{( 7 ) 7} 2 _>; p ^{( 7} ^,_{2 =}

Формулы (20), (21) получены для произвольной функции h ( y ), удовлетворяющей требованиям из (6).

Полагая выполненным неравенство (21), для поля в случае степенного профиля показателя преломления запишем функцию h (γ) вместе с выражением для поля (20):

h(У) = У" (" = 1,2,3,••■П x i f i    i+4V2у

^ E (у ) = ye exp f2/------- n+2

--dy Zx

У

= ln

r

V

i )

* 2 f

к 1 + 4V² h ( y ) y² Y

d y, (18)

х exp { - ау ²/2 ^ .

и согласно (8), (10) и (15) получим для поля

С помощью вспомогательного интеграла

E ( у )    ¹ exp U 2 J

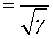
J 1 + 4V² h ( у ) у²    '

-------—--dy ^x

m c\ 1 + ax , J---------dx =

у

x exp { - ay2/2Y          (19)

= ^& ™ ₊ in J m

V1 + ax™ - 1

V1 + ax™ + 1

1 m

I , (22)

Поскольку в случае ступенчатого волновода h ( у ) - 0 ( у e ( 0,1 ) ) , то выбираем знак плюс – в этом случае (19) сводится к выражению (10).

Окончательно получаем предыдущее выражение для поля, в случае степенного профиля показателя преломления, принимает окончательный вид (в (22) a = 4V 2, m = n + 2):

h ( у ) = _Z ” ( n = 1,2,3, - ) ^

E ( 7 ) =    exp UJ

' 1 J1 + 4V² h ( 7 ) 7²    '

- ¹  --------------d7 ^x

^ E n ⁽ У ^{) =} Л= У

1 ₊ 4V² * 2 -1

1 ₊ 4 V² у ^{п + 2} +1

14 n

X

x exp ) - «7 2/2 } .           (20)

Подчеркнем, что при у ^ 0 поле не обращается в нуль, согласно предыдущему выражению.

Дифференцируя р'_х ( у ) из (18), условие (17) запишем в виде

1 ₊ 2 [ 2 V²h' ( у ) у ³ - 1 ] к 1 + 4 V² h ( у ) у²

<< 2 V ² h ( у ) у ².(21)

x exp j —1— 1 + 4V2у"+2 [x I n + 2                  I xexp|-±у2/2^.         (23)

Наконец, для безразмерной нормированной энергии W norm _{( n} ) ( V ) (отношение энергии поля (23) W gr ^ _n ^ ( V ) = 1

= J Е П ( У ) ydy к энергии поля (10) 0

для ступенчатого профиля W st ( V ) = 11

= j E 02 ( у ) ydy = j exp ( -ау ² ) ydy в одномодовом режиме) находим (несмотря на выбранный вариант в (13), не снижая общности, интегрируем по γ от нуля до единицы) ( К Е ( 0,5; 2,4 ) , n = 1,2,3,4,5 )

W V} = norm ( n )

I 1

_< j exp ( -ay ) y d y _

I 0

0,32 V ²

1 - exp( - 0,16 V ²)

х exp

W (n)(V) _ Wst (V) 2a E1 - exp (-a Xl}_ if 01

^^^^^^е

12 n

V1 + 4V2xn+2 -1 I i        =— I x

V1 + 4 V² x n ⁺ 2 + 1 )

•exp ( -0,16 V ² x ²

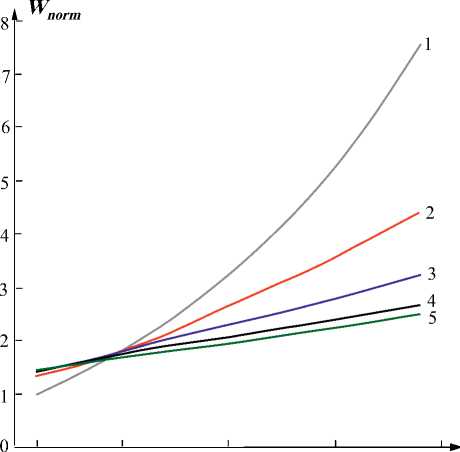
На рисунке для слабопроводящего оптоволокна с градиентным профилем показателя преломления, без учета поляризации в одномодовом режиме в случае степенного профиля показателя преломления при n = 1, 2, 3, 4, 5, построены зависимости «нормированной» энергии W_norm ( _n ) от волноводного параметра. Показано, что до значения V _c ~ 0,9 быстрее растет энергия для профиля с n = 1 (но в точке V _c~ 0,9 для всех рассмотренных степеней энергия совпадает), а после этого значения с резким отрывом растет энергия для профиля с n = 1, а для n > 1 рост энергии уменьшается с увеличением n .

Если сравнить результаты с данными нашей предыдущий работы [18], посвященной анализу поля и энергии сла-бопроводящего оптоволокна, с учетом поляризации в одномодовом режиме в случае степенного профиля показателя преломления, рассмотренного для случаев n = 2, 3, то учет поляризации сводится к смещению точки Vc от значения 0,9 до значения 1,55.

Обсуждение и заключение

Как видно из рисунка, при изменении параметра V от значения 0,5 до 2,405, согласно формуле (11), нормированная энергия W_norm растет от 1 до W_{norm (max)} ≈ 7,5 для профиля с n= 1, до W_norm ( _min) ~ 2 для профиля с n = 5. Для всех рассмотренных профилей значения соответствующих энергий превышают энергии ступенчатого профиля для соответствующих значений параметра V . Исключая мало применяемый профиль с n= 1, видим, что наиболее энергоэффективным из всех степенных профилей оказывается профиль с n = 1, что подтверждается экспериментальными данными⁴.

Поскольку согласно формуле (5)

| to 2 л          2    2

V = k p NA = ( k = - =— , NA = n co_co - n_d

(    c X

=2лр V no- nd, X и энергоэффективность возрастает с ростом параметра V, то при постоянной численной апертуре NA в рассматриваемом слабонаправляющем случае (NA << 1 – малая разность между показателем преломления в сердцевине волокна и показателем преломления оболочки) параметр V можно повышать либо уменьшением длины волны, либо увеличением радиуса сердцевины.

Данная работа посвящена исследованию зависимости поля и энергии в градиентных волокнах со степенным профилем показателя преломления. Результаты получены в общем виде для произвольной степени показателя преломления и проиллюстрированы для выбранных степеней (в предыдущей

0,5        1           1,5           2          2,5 V

Р и с. Зависимость нормированной энергии W_norm от волноводного параметра V для профиля показателя преломления n : 1 – профиль n = 1; 2 – профиль n = 2;

3 – профиль n = 3; 4 – профиль n = 4; 5 – профиль n = 5

F i g. Dependence of the normalized energy W_norm on the waveguide parameter V for the refractive index profile n : 1 – profile n = 1; 2 – profile n = 2; 3 – profile n = 3; 4 – profile n = 4; 5 – profile n = 5

работе [18] для случаев n = 2, 3, а в настоящей для n = 1, 2, 3, 4, 5). При этом аналитические расчеты были проведены разными методами. Показано, что учет поляризации сводится к смещению точки пересечения V_c от значения

0,9 до значения 1,55. Полученные результаты, с учетом конкретных приложений, могут быть применены при конструировании энергетически выгодного профиля сердцевины волокна и для анализа передачи информации.

Поступила 27.06.2022; одобрена после рецензирования 12.09.2022; принята к публикации 19.10.2022

Technologies, machinery and equipment                                                      597

Об авторах:

Все авторы прочитали и одобрили окончательный вариант рукописи.

Submitted 27.06.2022; approved after reviewing 12.09.2022; accepted for publication 19.10.2022

All authors have read and approved the final manuscript.

Technologies, machinery and equipment