Исследование поляризационного преобразования и взаимодействия обыкновенного и необыкновенного пучков в непараксиальном режиме

Анизотропные вещества широко используются в оптике для разнообразных практических задач, в том числе для преобразования одних свойств электромагнитного излучения в другие. Разработка методов, позволяющих решить указанную задачу, является весьма актуальной.

Распространение лазерных мод высокого порядка в среде с сильной анизотропией приводит к сложным поляризационно-модовым преобразованиям, связанным с наличием орбитального углового момента у таких пучков. Для линейно-поляризованного излучения происходит периодическое перераспределение энергии между двумя поперечными компонентами, а для пучка с круговой поляризацией энергия перекачивается из исходного пучка в вихревой пучок второго порядка и обратно.

Известно, что для Гауссова пучка c круговой поляризацией лишь половина энергии преобразуется в вихревой пучок, причём на бесконечном расстоянии [1 –4]. Наиболее заметно анизотропные эффекты проявляются для пучков Бесселя [5–7] в связи с особой структурой их пространственного спектра. Аналогичное преобразование для Гауссовых мод не столь выражено [7]. Для достижения большей эффективности преобразования используются каскады анизотропных элементов, что увеличивает габариты устройств и приводит к снижению энергетической эффективности. В работе [8] было показано, что можно достичь большей эффективности преобразования для элегантных мод Лагерра–Гаусса (ЛГ), хотя для обычных мод ЛГ с высоким радиальным порядком и нулевым угловым порядком эффективность не превышает 51 %.

Для анализа таких явлений часто используется параксиальная модель распространения [4]. В рамках этой модели преобразование со 100% эффективностью невозможно получить в принципе, а реально используемые кристаллы с длиной в несколько сантиметров не позволяют достичь даже 50% эффективности преобразования.

В работе [7] было показано, что для обычных мод ЛГ высокого порядка в непараксиальном режиме характерно поведение, близкое к Бесселевым модам, но только в ближней зоне дифракции. Непараксиальные модовые лазерные пучки при распространении вдоль оси

кристалла испытывают периодическое изменение интенсивности, связанное с интерференцией обыкновенного и необыкновенного лучей. Теоретически было показано [7], что использование непараксиальных пучков Бесселя позволяет достичь эффективности преобразования, близкой к 100% на малых (менее 1 см) длинах распространения вдоль оси одноосных кристаллов. Экспериментальное преобразование непараксиального циркулярно-поляризованного пучка Бесселя нулевого порядка в вихревой пучок второго порядка показано в работе [9].

В целом применение указанных методов должно привести к существенному уменьшению габаритов, упрощению и удешевлению оптической системы для формирования оптических вихрей с расширением её функциональных возможностей.

В данной работе на примере линейно-поляризованного пучка Бесселя нулевого порядка численно и экспериментально исследуются поляризационные преобразования, происходящие в кристалле. Эти преобразования обеспечивают возможность взаимодействия обыкновенного и необыкновенного пучков, которое становится существенным лишь в непараксиальном режиме.

1. Теоретические основы

Распространение осесимметричного поля f ( r ) с однородной поляризацией ( p_x , p_y ) вдоль оси кристалла можно описать в компактной форме [5, 9] как суперпозицию обыкновенного и необыкновенного пучков:

E (ρ, θ, z ) =

= E o (ρ,θ, z )+ E e (ρ,θ, z )=

' P J o ( k PG) + p ⁺ J 2 ( k PG)

k 2 ~ ¹ x ^{041       1    241}

= — J P y J o ( k po) - P"J 2 ( k po)

2 ∞

×

V

×exp [ ikz γ _o (σ) ] F ₀ (σ)σdσ+

A

P x^J 0^{( k} P^{G ) -} P + ^J 2^{( k} P^{G )}

k 2 ∞

+ — J P y J ₀( k P^{o )} + p " J 2^{( k} P^{o )}

2 ∞

×

-( P x cos 6 + P y sin 6) V

×exp [ ikz γ _e (σ) ] F ₀ (σ)σdσ,

2 iEG T.

^o J 1 ( k ρσ)

E e Ye (o)         J

где £ _о , £ e - соответствующие диэлектрические проницаемости; 6 - угловая координата; р , z - линейные координаты в цилиндрической системе координат; к = 2 п Г к - волновой вектор; о - пространственная частота; у _о ( о ), у e ( о ) - величины, определяющие направление распространения обыкновенного и необыкновенного пучков:

Yо (о) = 4 £ о -о2,

Y e ( о ) = V £ о -о ²( £ о /£ e ) ,

F о ( о ) - пространственный спектр падающего на кристалл излучения:

^

^F 0 ^{( о )} = J f ⁽ r ) J 0 ⁽ kr ^{о )} r d r ,                        ⁽³⁾

p+ = p, cos 26+ p sin 26, x y                                         (4)

p = py cos26-px sin26, px, py – координаты вектора поляризации падающего излучения, Jn (x) – функция Бесселя n-го порядка. Если переписать выражение (1) в следующем виде [9]:

E ( P , 6 , z )

k ²

и

J

'p J0 (кро)'

pyJ0 ( k Ро) [exp ( ikzYо (о)) + exp ( ikz Ye (о))] F0(о) о dо

+

оV            /

k

+

и

J

p + J2 ( кРо) [exp (ikzYо (о))- exp (ikzYe (о))]-p-J2 (кро)[exp(ikzYо (о))-exp(ikzYe (о))]

^ ,( о ) о d о ,

-2 i ( px cos 6+ py sin 6)— о . J1 ( k Ро) exp ( ikz Ye (о)) V                            £e Ye (о)                            )

то становится очевидно, что за счёт различия набега фазы обыкновенного exp( ikzg_o ( о )) и необыкновенного exp( ikzg e ( о )) пучков будет происходить периодическая перекачка энергии между первым слагаемым, имеющим ненулевое значение на оптической оси, и вторым слагаемым, имеющим на оптической оси нулевое значение.

Эти рассуждения приводят к выводу, что изменение интенсивности пучка в кристалле связано с суперпозицией (интерференцией) обыкновенного и необыкновенного пучков. Однако такой вывод находится в противоречии с классическими свойствами ортогональности поляризационных состояний обыкновенного и необыкновенного пучков.

Попробуем разрешить это противоречие.

При падении коллимированного однородно-поляризованного излучения под углом к оптической оси кристалла происходит его разделение на обыкновенный и необыкновенный пучки. Считается, что эти пучки поляризованы ортогонально и поэтому не могут интерферировать между собой. Однако в случае появления наклона лучей, например, при падении на кристалл Бесселева пучка будет наблюдаться семейство обыкновенных и необыкновенных лучей (рис. 1), которые идут от разных колец и сходятся на оси в разных точках, взаимодействуя при этом, как следует из (5).

Взаимодействие будет происходить в связи с преобразованием исходной поляризации падающего (параллельного) пучка при возникновении наклона пучка [10]. Рис. 2 иллюстрирует поляризационное преобразование для наклонных пучков в различных плоскостях. В частности, для падающего пучка, исходно поляризованного вдоль оси x, лучи, преломлённые в меридиональной плоскости (перпендикулярной оси поляризации), будут сохранять исходную поляризацию. Для лучей, преломлённых в сагитталь- ной плоскости (параллельной оси поляризации), происходит частичное (в зависимости от угла наклона) преобразование в z-компоненту. Для промежуточных углов с осью х будет происходить преобразование как в z-, так и в y-компоненты. Максимальная проекция на ось y (перпендикулярную оси поляризации) достигается в диагональных плоскостях.

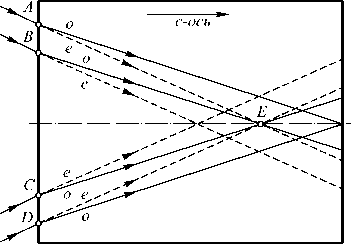
Рис. 1. Интерференция семейства обыкновенных и необыкновенных лучей в кристалле

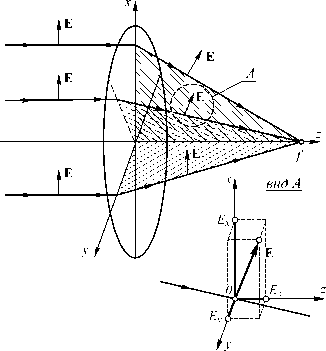
Рис. 2. Иллюстрация поляризационного преобразования для наклонных пучков в различных плоскостях

Именно результат взаимодействия этих преобразованных x - и y-компонент обыкновенного и необыкновенного лучей мы наблюдаем в виде интерференционной картины.

Это взаимодействие является полным аналогом классической интерференции. Проверим приведённые выше рассуждения на основе моделирования и экспериментов.

В частности, у -компонента будет отсутствовать в сечениях z = z m :

zm =λm (γo (α) - γe (α)) ≈

2Х,^₀ £ m ^a 2 (^£ o ^-£ e )

m = 1, 2, 3

2. Результаты моделирования для линейно-поляризованного пучка Бесселя нулевого порядка

Рассмотрим распространение вдоль оси кристалла исландского шпата ( е o = 2,75; £ e =2,21) пучка Бесселя нулевого порядка f ( r ) = J 0 ( k a r ), где a - параметр пучка, соответствующий наклону лучей к оптической оси т ( a = sin т ).

Для пучков Бесселя выражение (5) можно существенно упростить:

и принимать максимальное значение на расстояниях z = z p :

zp = Ц2p +1)/2(yo (a)-ye (a)) == XjTo£e(2p +1)/a2 (eo-£e), p = 1,2,3.

Распределение интенсивности пучка в кристалле (без учёта продольной компоненты) также будет претерпевать периодические изменения:

Г Рх 2

E(P,6, z) = 2 Py Jо(kaP) C(z) +

| E x ( p , 6 , z )|² =

= 0,5 [| C ( z )|² J ₀² ( k ap ) + 1 S ( z )|² J 2 ( k pa ) ] ,

+

-

к

л к и 7

( p_x cos 2 6 + p_y sin 2 6 ) J ₂ ( k pa ) S ( z )

( p_x sin 2 6 - p y cos 2 6 ) J ₂ ( k pa ) S ( z )

-2 i ( p_x cos 6 + p y sin 6 ) ( e _o I £ e ) x x ( a I y e ( a )) J i ( k pa ) exp ( ikz у e ( a ) )

к

где C ( z ) = exp ( ikz у _o ( a )) + exp ( ikz у _e ( a )), S ( z ) = exp ( ikz у _o ( a )) - exp ( ikz у e ( a )). Для линейной x -поляризации:

а именно: на расстояниях (9) будет соответствовать пучку Бесселя нулевого порядка, а на расстояниях (10) -пучку Бесселя второго порядка. На промежуточных расстояниях будет соответствующая суперпозиция.

В нашем исследовании интересно также выяснить покомпонентное распределение в обыкновенном и необыкновенном пучках. Для этого вернёмся к выражению (1) и запишем его в рассматриваемом случае падения на кристалл пучка Бесселя нулевого порядка: E (p, 6, z ) = E o (p, 6, z ) + E e (p, 6, z ) =

" p x J a ( k pa) + ( p x cos 26 + p y sin 26 ) J ₂( k pa)

E ^x - lin ( p , 6 , z ) =

Г 0,5 )

к 0

J0 (kap) C (z) +

= 2 p y J a ( k pa) - ( p y cos 26- p x sin

к

xexp[ikzyo (a)] +

26 ) J ₂( k pa) x

+

-

к

cos 2 6- J ₂( k pa ) S ( z )

sin 2 6- J ₂( k pa ) S ( z )

- 2 i cos 6^ — O-x

^£ e y e (^a)

x J1 (kpa) exp (ikzуe (a))7

.

Интенсивность поперечных компонент:

I E x ( p , 6 , z )| ² = 0,5 | C ( z )| ² J о ² ( k ap ) +

+ 0,51 S ( z )| ² J ₂ ² ( k pa ) cos² 2 6 ,                  (8)

|E_y ( p , 6 , z )| ² = 0,51 S ( z )| ² J ₂ ² ( k pa ) sin² 2 6 .

Как следует из (8), при распространении в кри

сталле изначально x -поляризованного поля происходит поляризационное преобразование и возникает ортогональная y -компонента. Интенсивность этой компоненты меняется в зависимости от пройденного вдоль оси кристалла расстояния z в соответствии с выражением | S ( z )|² = 2-2cos[ kz ( у _o ( a )- у e ( a ))] .

+

p x J 0 ( k pa) - ( p, cos 26 + p y sin p y J a ( k pa) + ( p y cos 26- p x sin

26 ) J 2 ( k pa)

26 ) J 2 ( k pa)

×

2 i e

^- ( p x ^{cos 6+} p y ^{sin 6} )---- ^J 1 ^{( k} p^{a )}

к                    y       eeye (a)             7

xexp[ ikz y _e ( a ) ].

Для линейной x -поляризации:

E ^{x -} lin ( p , 6 , z ) = 2

г J ₀ ( k pa ) + cos 2 6 J ₂ ( k pa )²

кxexp[ikzy0 (a)] +

sin 2 6 J ₂( k pa ) 0

k

×

+

J ₀ ( k pa ) - cos 2 6 J ₂ ( k pa ) - sin 2 6 J ₂( k pa )

- cos 6 ^i ^£ ° ^a J 1 ( k p a ) ε _e γ _e ( α )

exp [ ikz y e ( a ) ] .

В (13) первое и второе слагаемые, соответствующие обыкновенному и необыкновенному пучкам, не являются ортогональными. Заметим, что необыкновенный пучок содержит продольную компоненту, пропорциональную функции Бесселя первого порядка, но её вклад в общую интенсивность даже при больших числовых апертурах невелик [6].

На расстояниях, когда пучки оказываются синфазными, т.е. выполняется условие (9) и exp [ ikz γ e ( α )] = exp [ ikz γ o ( α )], будет наблюдаться пучок Бесселя нулевого порядка:

E ^{x - lin} ( ρ , θ , z = z m ) ≈

Jo( k pa) 0 ч - cos «’^ Ji(kpa), exp[ikzYo (a)] .

Если же пучки находятся в противофазе, т.е. выполняется условие (10) и exp [ ikz γ e ( α )] = –exp [ ikz γ o ( α )], то будет наблюдаться пучок Бесселя второго порядка:

E ^{x - lin} ( ρ , θ , z = z p ) ≈

cos 2 θ J ₂ ( k ρα ) sin 2 θ J ₂ ( k ρα )

г..   ( я (15)

^exP [ ikz Y o (^a) ] .

(- cos e (2 i e _o a / ( e _e y _e ( a ))) J 1 ( k pa ) J

Ниже приведены результаты моделирования распространения поля вдоль оси кристалла исландского шпата при падении на него линейно-поляризованного пучка Бесселя нулевого порядка f ( r ) = J ₀ ( k α r ) с длиной волны λ = 0,6328 мкм и параметром α = 0,505.

На рис. 3 показана зависимость интенсивности пучка на оптической оси от пройденного в кристалле расстояния. Минимумы интенсивности соответствуют преобразованию в пучок Бесселя второго порядка, а максимумы – возвращению к исходному состоянию. В соответствии с выражением (9) период изменений равен ∆ z ≈ 33,6 мкм, что на 5 % больше, чем получилось в результате численного моделирования ∆ z ≈ 32 мкм. Эта погрешность связана с приближённой аппроксимацией в (9).

В табл. 1 –3 приведены результаты моделирования, наглядно показывающие распределение интенсивности как по компонентам электрического поля E , E , E , так и для обыкновенного и необыкновенно-x, y, z, го пучков. Поперечные сечения интенсивности (негатив) размером 5 × 5 мкм показаны на расстоянии z1 =32 мкм, что соответствует синфазному сложению обыкновенного и необыкновенного пучков, а также максимальному значению на оптической оси, и при z2 =48 мкм, что соответствует противофазному сложению обыкновенного и необыкновенного пучков, а также минимальному значению на оптической оси.

Как видно из табл. 1 –3, необыкновенный пучок имеет продольную компоненту (третья строка), про- порциональную функции Бесселя первого порядка, но её вклад не слишком велик.

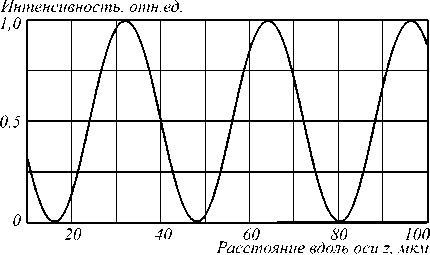
Рис. 3. Интенсивность поля на оптической оси в зависимости от пройденного в кристалле расстояния

На расстоянии z 1 =32 мкм синфазного сложения обыкновенного и необыкновенного пучков (табл. 1) y -компоненты взаимно компенсируются, и общая интенсивность выглядит как пучок Бесселя нулевого порядка. На расстоянии z 2 =48 мкм противофазного сложения обыкновенного и необыкновенного пучков (табл. 2) y -компоненты взаимно компенсируются, и общая интенсивность выглядит как пучок Бесселя второго порядка.

Из табл. 1 –3 наглядно видно, что, хотя полная интенсивность (последний столбец) обыкновенного и необыкновенного пучков остаётся одинаковой на любом расстоянии, распределение интенсивности их суперпозиции существенно изменяется.

Также из табл. 1 –3 хорошо видно, что распределение интенсивности для y -компоненты имеет максимальное значение на диагоналях, а для z -компоненты – вдоль оси поляризации. Это полностью соответствует рассуждениям в первом разделе о поляризационных преобразованиях при преломлении лучей. Именно так выглядят коноскопические картины, подтверждающие поляризационные преобразования в кристаллах.

3. Результаты эксперимента для линейно-поляризованного пучка Бесселя нулевого порядка

Рассмотренные выше периодические преобразования происходят только в анизотропной среде. При выходе светового пучка из кристалла фиксируется то распределение поля, которое было достигнуто непосредственно на границе анизотропной и изотропной сред.

Чтобы кристалл эффективно производил преобразование падающего пучка Бесселя в пучок более высокого порядка, необходимо выполнение условия (9). Для пучков с высокой числовой апертурой преобразование происходит на расстоянии несколько десятков микрометров, поэтому на длине кристалла размером несколько сантиметров происходит множество периодов преобразований. При этом незначительное изменение числовой апертуры, внесённое, например, изменением кривизны волнового фронта падающего пучка, позволяет совмещать плоскость, где происходит нужное преобразование, с плоскостью выходного торца кристалла.

Табл. 1. Покомпонентное продольное распределение интенсивности (негатив) на расстоянии z = 32 мкм (максимальное значение на оптической оси)

		I E x I 2 , arg Ex	Ey 2 , arg Ey	1 E z 1 2 , arg Ez	1 E 2
s s N	Обыкновенный
	Необыкновенный	[©]
	Суперпозиция	1©

Табл. 2. Покомпонентное продольное распределение интенсивности (негатив) на расстоянии z = 40 мкм (промежуточное значение на оптической оси)

		I E x I 2 , arg Ex	2 Ey , arg Ey	1 E z 1 2 , arg Ez	i E 2
s о II N	Обыкновенный
	Необыкновенный
	Суперпозиция

Табл. 3. Покомпонентное продольное распределение интенсивности (негатив) на расстоянии z = 48 мкм (минимальное значение на оптической оси)

Обыкновенный

Суперпозиция

E x ² , arg E_x

E_y , arg E_y

E z ² , arg E_z

^{E 2}

Необыкновенный

Для формирования пучков Бесселя нулевого порядка с различной числовой апертурой был изготовлен амплитудный ДОЭ [11 – 13] диаметром 40 мм на стеклянной подложке с периодом колец 4 мкм (для λ = 0,633 мкм соответствует α = 0,16). Структура ак-сикона включает хромовую маску, сформированную на станции лазерной записи CLWS-200 методом термохимического окисления с последующим химическим удалением немаскированных участков.

Для исследования поляризационного преобразования и взаимодействия обыкновенного и необыкно- венного пучков была собрана оптическая схема, показанная на рис. 4. Источником излучения служил гелий-неоновый лазер ЛГН-207А с линейно-поляризованным излучением. Расширение лазерного пучка производилось объективом 10× и двояковыпуклой линзой диаметром 50 мм с фокусным расстоянием 500 мм. В качестве анизотропной среды использовался одноосный кристалл исландского шпата с размерами 8×8× 15 мм. С-ось кристалла ориентировалась параллельно оптической оси схемы. Точное сведение обыкновенного и необыкновенного пучков обеспечи- валось двумерной угловой оправой. Увеличение размеров выходного пучка обеспечивалось 20× объективом, установленным в трёхкоординатную оправу. Распределение интенсивности выходного пучка фиксировалось чёрно-белой USB-видеокамерой DCM 310 с разрешением 3 МПкс и разрядностью АЦП 8 бит. Исследование поляризации выходного излучения осуществлялось плёночным анализатором.

На рис. 5–7 показаны экспериментальные результаты преобразования линейно-поляризованного по горизонтали пучка Бесселя нулевого порядка в пучок

Бесселя второго порядка с помощью кристалла исландского шпата. На выходе анализатора получилась ситуация, соответствующая противофазной суперпозиции обыкновенного и необыкновенного пучков.

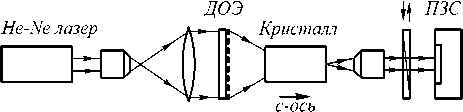
Рис. 4. Оптическая схема экспериментальной установки

б)

Рис. 5. Сведение обыкновенного и необыкновенного пучков без анализатора

Рис. 6. Сведение обыкновенного и необыкновенного пучков с положением анализатора параллельно поляризации падающего пучка

б)

Рис. 7. Сведение обыкновенного и необыкновенного пучков с положением анализатора ортогонально поляризации падающего пучка

Для подтверждения факта интерференции обыкновенного и необыкновенного пучков показаны картины сведения этих пучков вдоль одной оси, соответствующей оси кристалла. На рис. 5 показан процесс сведения пучков без анализатора; на рис. 6 – процесс сведения пучков с положением анализатора параллельно поляризации лазерного пучка; на рис. 7 – процесс сведения пучков с положением анализатора ортогонально поляризации лазерного пучка.

Сравнение результатов экспериментального исследования (рис. 5–7) и численного моделирования (табл. 1 –3) показывает их полное соответствие. Таким образом, теоретически и экспериментально уста- новлено наличие в изначально обыкновенном и необыкновенном пучках обеих ортогональных поперечных компонент электрического поля в условиях непараксиального режима. Обоснована и показана возможность интерференции этих пучков, т. е. сложения соответствующих компонент.

Заключение

В работе рассмотрено преобразование непараксиального Бесселевого пучка в кристалле исландского шпата. Аналитически и численно показано наличие в обыкновенном и необыкновенном пучках обеих ортогональных поперечных компонент электрического по- ля. Этот факт обеспечивает возможность интерференции двух пучков и приводит к периодическому изменению картины полной интенсивности.

Такое поляризационное преобразование становится заметным только в непараксиальных условиях падения излучения на кристалл. Также эффект усиливается при увеличении разности показателей преломления для обыкновенного и необыкновенного пучков. Результаты экспериментов полностью подтвердили правильность рассмотренного подхода.

Хонина С.Н., Карпеев С.В., Морозов А.А. выражают благодарность за финансовую поддержку Российскому научному фонду (грант 14-19-00114).

Паранин В.Д. выражает благодарность за финансовую поддержку Министерству образования и науки РФ.