Исследование полумарковского потока в условии предельно редких изменений его состояний

В данной статье рассматривается полумарковский поток (SM-поток, Semi-Markovian process), который является наиболее общей моделью потоков однородных событий [1].

Дадим определение полумарковского потока, для чего рассмотрим двумерный однородный марковский случайный процесс { £ ( n ), т ( n )} с дискретным временем. Здесь £ ( n ) - эргодическая цепь Маркова с дискретным временем и матрицей P = [p _{v k} ] вероятностей перехода за один шаг [2]; процесс т ( n ) принимает неотрицательные значения из непрерывного множества.

Далее определим марковскую переходную функцию F ( v , x , k , y ) для процесса { £ ( n ), т ( n )}:

F ( k , x ; v, y ) = P { c ( n + 1 ) = k , т ( n + 1 ) <  x | ^ ( n ) = v, т ( n ) = y } .

Будем рассматривать такие двумерные процессы { £ ( n ), t ( n )}, для которых выполняется следующее равенство:

F (v, x; k, y ) = F (v, x; k), т. е. F(v, x, k, y) не зависит от значенийy процесса т(n).

Обозначим

F ( ^k , x ;^v ) = A v k ( x ) = P { ^ ( n ⁺ 1 ) = ^k ,^т ( n ⁺ 1 ) <  x ^ ( n ) = v } . (1)

Матрицу A ( x ) с элементами A _{v k} ( x ) будем называть по-лумарковской.

Случайный поток однородных событий t1 < t2 < ... < tn < tn+1 < ...

будем называть полумарковским потоком, или SM-потоком, заданным матрицей A ( x ), если для моментов t_n наступления его событий выполняется следующее равенство:

tn+1 = tn +T(n + 1) .

В силу (1) матрица переходных вероятностей цепи Маркова £ ( n ) определяется равенством

P = A («).

Эту цепь для полумарковского потока назовем вложенной цепью Маркова.

Для элементов полумарковской матрицы в общем случае имеет место мультипликативная форма, которую можно записать в виде

Avk (x ) = P {^ (n + 1) = k, t( n +1)< x| ^ (n ) = v} =

= P{t(n +1) < x, |^(n) = v, £(n +1) = k}x

X ^P { ^ ( ^{n +} 1 ) = ^k ,| ^ ( ⁿ ) = ^v } = G v k ( x ) p v k , где G _{v k} ( x ) - условная функция распределения длины интервала полумарковского потока при условии, что в начале этого интервала вложенная цепь Маркова приняла значение v , а в его конце примет значение k . В силу равенства

A v k ( ^x ) = ^G v k ( ^x ) P v k                ⁽²⁾

матрицу A ( x ) можно записать в виде произведения Адамара

A (x ) = G (x )• P                (3)

двух матриц G ( x ) и P , и можно полагать, что полумарков-ский поток задан двумя матрицами G ( x ) и P .

Состоянием полумарковского потока в момент времени t n < t <  t + 1 назовем состояние k его вложенной цепи Маркова, принятое в начале интервала ( t_n , t_{n + 1}).

Исследование полумарковского потока будем проводить в условии предельно редких изменений состояний (ПРИС) потока, при котором переход из одного состояния вложенной цепи Маркова в другое осуществляется крайне редко

Условие предельно редких изменений состояний по-лумарковского потока формализуется следующим равенством для матрицы P ( 5 ) вероятностей переходов его вложенной цепи Маркова:

P(5) = I + 5-Q ,                 (4)

где 5 - некоторый малый параметр ( 5 ^ 0); I - единичная диагональная матрица.

Матрица Q c элементами q _{v k} аналогична матрице инфинитезимальных характеристик и имеет такие же свойства, т. е. при k * v элементы матрицы q _{v k} > 0 и выполняются равенства

Z q v k = 0, Z q v k = - q kk . k            k *v

Запишем полумарковскую матрицу для SM-потока в условии ПРИС:

• – при k = ν

A k ( ^x , ⁵) = ^P { ^ C ^{n +} 1 ) = ^k , ^t( ^{n +} 1 ) <  x | ^ C ⁿ ) = ^k } = ^G kk ( ^x ){ ^{1 +5-} q kk } ;

• - при k * v

A v k ( ^x , ⁵) = ^P { ^ C ^{n +} 1 ) = ^k , ^t( ^{n +} 1 ) <  ^x | ^ C ⁿ ) = ^v } = ^G v k ( ^x )^-5- q v k .

С другой стороны, подставляя (4) в мультипликативную форму записи (3) полумарковской матрицы, получим:

A ( x , 5 ) = G ( x ) ■ { I + 5 ■ Q } .              (5)

Обозначим через m ( t ) число событий полумарковс-кого потока, наступивших за время t на интервале [0, t ).

Процесс m ( t ) является немарковским, поэтому необ-

ходимо его марковизировать методом дополнительных переменных. Для этого введем переменную z ( t ) - длину интервала от момента времени t до момента наступления очередного события в рассматриваемом SM-потоке.

Однако двумерный процесс { m ( t ), z ( t )} не является марковским, поэтому рассмотрим еще один случайный процесс 5 ( t ) с кусочно-постоянными реализациями, непрерывными слева, определенный равенством

⁵ ( t ) = ^ ( n ⁺ 1 ) ,

где I - единичная матрица; вектор R ( z , 5 ) определяет начальное условие задачи (11) с компонентами R ( 5 , z , 5 ) и, как показано в [4], имеет вид

R(z,5) = к, (5)rj(P(5)-A(x,5))dx, здесь r - стационарное распределение вероятностей значений вложенной цепи Маркова ^(n), а величина к 1(5) определяется как             1

к1 (5) = ^7KF, rA (5) E где A (5) = j (P (5)- A(x, 5)) dx.

Найдем асимптотическое распределение вероятностей числа событий, наступивших в SM-потоке за время t , в условии предельно редких изменений состояний потока.

Обозначим

lim H ( u , z , t , 5 ) = H ( u , z , t ) .

5^0 v          / X /

если t n <  t <  t n _{+ 1}. Этот процесс на интервале ( t n , t + 1 ] принимает и сохраняет то значение, которое вложенная цепь Маркова £ ( n ) принимает в начале следующего интервала [1].

Определенный таким образом трехмерный случайный процесс { 5 ( t ), m ( t ), z ( t )} с двумя дополнительными переменными 5 ( t ) и z ( t ) является марковским с непрерывным временем и для распределения вероятностей

P ( 5 , m , z , t , 5 ) = P { 5 ( t ) = 5 , m ( t ) = m , z ( t ) <  z } (6)

В задаче (11), с учетом (12), выполним предельный переход при 5 ^ 0. Тогда для H ( u , z , t ) получим совокупность независимых задач Коши [3; 4]:

' ^d H ^{( u} , z , t ) = ^д H ^{( u} , z , t ) I ^d H ^{( u} ,0, t ) ( e ju A _{( z} ) - 8 <  8 1 8 z 8 z ^{{ }} ’(13)

нетрудно составить систему дифференциальных уравнений Колмогорова

8P ( 5 , m , z , t , 5 ) 8P ( 5 , m , z , t , 5 )

8P ( 5 , m ,0, t , 5 )

8 z

to

+ e

8z

8P ( v, m - 1,0, t , 5 )

8z

A V k ⁽ z ) ,

при заданном начальном условии

I P ( 5 ,0, z ,0,5 ) = R ( 5 , z , 5 ) , P ( 5 , m , z ,0,5 ) = 0, m >  1,

где функция R ( 5 , z , 5 ) - стационарное распределение двумерного марковского процесса { 5 ( t ), z ( t )}.

Обозначим функции

to

H ( 5 , u , z , t , 5) = E e^J™P ( 5 , m , z , t , 5),         (9)

m = 0

где J = V—1 - мнимая единица. Для этих функций из системы (7) и начальных условий (8) можно записать следующую задачу Коши:

8H ( 5 , u , z , t , 5 ) 8H ( 5 , u , z , t , 5 )

-

81                8z

8H ( 5 , u ,0, t , 5 )        »8H ( v, u ,0, t , 5 )

+ e^J У

8z             v = 1         d z

H ( 5 , u , z ,0,5 ) = R ( 5 , z , 5 ) .

-A v k ( ^z ’ ⁵ ) ’

Обозначим

H (u, z, t, 5 ) = { H (1, u, z, t, 5), H (2, u, z, t, 5),...} и введем матрицу A(z, 5) с элементами Akv(z, 5), тогда из (10) получим

d H ( u , z , t , 5 ) ■        5 1

d HU , z , t , 5) 5 HU ,0, t , 8),             ,

(;,,) +     (;,,) {e,j A (z, 5) -1}, dz            dz

H ( u , z ,0,5 ) = R ( z , 5 ) ,

_ H (u, z ,0) = R (z), где lim P (5) = I; lim A (z, 5) = A (z); 5im A (5) = A;

lim к. ( 5 ) = к ; lim R ( z , 5 ) = R ( z ) .

5^0 ^{1 v} '      ¹    5^0 ^{v 7 v 7}

С учетом вида матрицы A ( z ), получим из (12) совокупность независимых дифференциальных уравнений

ВH ( 5 , u , z , t )    5 H ( 5 , u , z , t ) 5 H ( 5 , u ,0, t )

d z

d z

{ e^,JG„ ( z ) - 1 } . ⁽¹⁴⁾

Начальные условия имеют вид

H ( 5 , u , z ,0 ) = R ( 5 , z ) .

Решение задачи (14), (15) найдем, применяя преобразование Фурье-Стилтьеса:

Ф (5, u, a, t) = J eJaz dzH (5, u, z, t).

Функция ф ( 5 , u , б, t ) удовлетворяет уравнению

5 ф ( ⁵ , ^u , a, t )     .               5 H ( ⁵ , ^{u ,0,} t )(.„„.,, л

—----L = - j аф (5, u, a, t) + ejuGss (a)-1} (17) dt и начальному условию

Ф(5,u,a,0) = JejazdzH(5,u,z,0) = JejazdzR(5,z) = R*(5,a), (18) 00

to где G*55 ( a ) = j eJaz dzG55 ( z )■

Решение дифференциального уравнения (17) имеет вид

Ф (5, u, a, t) = e Jat x x jR* (5,a)+ jeJaT дHC5lJl0,I) (ejuG5*5 (a)- 1)dT.(19) А так как to lim ф (5, u, a, t) = j eJaz dzH (5, u, z, да) = 0, t ^to                     0

то, устремив t в равенстве (19) в бесконечность, получим

0 = R * ( 5 ,a ) + ^да e^{j a T d} H ^{( 5} _d u ^,0,T ) ( e^juG 55 ( a ) - 1 ) d t.

Из этого равенства найдем преобразование Фурье по д H ( 5 , и ,0, т ) т от функции-----------:

д z

^J e-H⁵^ dT = R ■ ( 5 , a ) ( 1 - e - G * ( a ))-

Выполним обратное преобразование Фурье:

^д H ( ⁵ , u ^{,0, т} )     1 1                      и - 1

------Я------- = J e j ^R ( ⁵ , ^a ) ( 1 ^- e ^G 55 ( ^a ) ) ^{d a} д Z        2П -j

Равенство (19), с учетом полученного преобразования, запишем в виде

Ф ( 5 , и , a, t ) = e"^{j a} t { R * ( 5 , a ) +

время t , имеет следующий вид:

J

p ^{( 0,}t ) = ¹ -^^ J ;2 ( 1 - e ')^E Г 5 ( 1 - G * ( y ) ) dy ’

2П -J У

L J         x ., V J

P ( m , t ) = -¹ J -2 ( 1 - e-^jyt ) E Г 5 ( 1 - G 55 ( У ) ) E e j-m G.” -1 ( У ^ dy ,

2П -j y '            s '' m

+ J e^j" J eR* ( 5 , У ) ( 1 - e j- G * ( У ) ) -' dy ( e j X ( a ) - 1 ) d т J . (20) 0 2n -j

Зная, что H ( 5 , и , j , t )= H ( 5 , и , t ) = ф ( 5 , и , 0, t ), R * ( 5 , 0) = к 1 rA₅ , G * ₅₅ (0) = 1, получим выражение для функции H ( 5 , и , t ):

где P ( m , t ) ~ P ( m , t ) .

Итак, выше нами были получены формулы, позволяющие найти асимптотическое распределение числа событий, наступивших в SM-потоке за время t . Это распределение также было найдено в допредельной ситуации методом интегральных преобразований [1]. Остается выяснить, насколько результаты, полученные с помощью метода асимптотического анализа, близки к результатам, полученным в допредельной ситуации. Для этого нужно найти величину

Л

^{H ( 5} , ^и , t ) = К rA +

+ ^ ^J J e j d T R * ( 5 , У ) ( 1 - е"С 55 ( У ) ) - 1 dy ( e j - 1 ) . (21) 2П -j 0

С учетом того, что je- jyT d т= ± (1 - e -jyt)

0 Jy^v

и

R * ( 5 , y ) = ^J e^jyzd z R ( 5 , z ) =

J z_{z x}      K1 r ( G * ( y ) - 1 )

= К Г J e^jy z ^d J ( ^{1 -} G 55 ( x ) ) ^dx =--------:--------,

0      0V            '              jy равенство (21) запишем в виде

A = max F (n, t)- F (n, t) , где F(n, t) - функция распределения, полученная с помощью асимптотического анализа; F(n, t) - функция распределения для допредельной ситуации, полученная в [1].

Пусть

G ( x ) = 1

H ( 5 , и , t ) = ^K 1 ^r 5 A 55 +

+ Kr ^J Л( 1 - e^y )( 1 - G * ( y ) )( 1 - e^G * ( У )У 1 dy ( e j - 1 )- (22) 2n -j y

Обозначим h ( и , t ) = E H ( 5 , и , t ). Тогда

s

(ej -1) К h (и, t) = E H (5, и, t) = 1 + ^------^ x

5                    2n

J 1                                                                       - 1

x J -2 ( 1 - e ' ) E r ( 1 - G ^ ( У ) )( 1 - e^JUG : 5 ( У ) ) dy -

-j y ^x            5

Зная, что

J

h ( и , t ) = E H ( 5 , и , t ) ® E H ( 5 , и , t , 5 ) = E e^Jll ” P ( n , t ),

5                      5                        П = 0

и раскладывая в ряд правую часть полученного равенства по степеням экспоненты e j , можно записать следующее асимптотическое равенство:

h ( и , t ) » EE e^P ( m , t ) =

, xm

(e -1) к J

= 1 +¹ , ' J ^F ( 1 - e-^jyt ) E r_s ( 1 - G * ( y ) ) E e- m G* ,; ( y ) dy =

2П -j y            sm

j

= 1 - 7¹ J “Г ( 1 - e-^jyt )E Г 5 ( 1 - G 55 ( У ) ) dy +

2n -j y

J

+ J ^2 ( 1 - e-^jyt )E Г 5 ( 1 - G * ( y ) ) E e j’m G*™ ^{- 1} ( y^dy .

2П -j y             5m

Тогда асимптотическое распределение вероятностей

P 1 ( m , t ) числа m событий, наступивших в SM-потоке за

Q = 1

1 - e

1 - e

1 - e

- 5 x

- 6 x

- 3

- 4

1 j ^,

-

- 2 x e

1 - e

1 - e ^--

^{- 6}

1 - e ^{- 10 x} 1

1 - e

1 - e

-

- 8 x

j , t = 6.

При заданных параметрах получим следующие значения отклонение результатов, полученных методом асимптотического анализа и в [1] для допредельной ситуации:

5	0,001	0,000 5	0,000 1	0,000 05	0,000 01
A	0,042 7	0,021 6	0,004 2	0,002 1	0,000 3

Распределения вероятностей числа событий в потоке, наступивших за время t = 6 и полученных с помощью асимптотического анализа и в допредельной ситуации, показаны ниже (рис. 1-3).

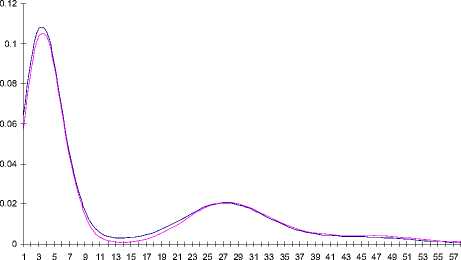
Рис. 1. Распределения вероятностей числа событий SM-потока при 5 = 0,001

Таким образом, получены асимптотические распределения вероятностей числа событий, наступивших в SM-потоке за время t. При уменьшении параметра 5 меняется отклонение результатов асимптотического анализа от

найденных в допредельной ситуации и при δ ≤ 0, 0001 оно составляет менее 1 %. Также следует отметить, что полученное распределение является многомодальным.