Исследование ползучести антифрикционных полимерных покрытий

Введение. Доказано [1], что в металлополимерных узлах трения с антифрикционными композиционными фторопластсодержащими покрытиями увеличение зазора трибосопряжения вызывают два процесса: изнашивание и вязкоупругая деформация при рабочих нагрузках.

Исследуемые полимерные покрытия, сформированные на базе тканых фторопластсодер-жащих каркасов и аморфного матричного связующего, являются вязкоупругими материалами [2]. Их ползучесть под нагрузкой, интенсифицированной объёмной температурой окружающей среды и генерируемой при трении, вносит существенный вклад в формирование зазора трибоконтакта, жёстко определяющего ресурс последнего.

Постановка задачи. Основной задачей проведённых экспериментальных исследований являлось установление вклада процесса ползучести композиционных полимерных покрытий в формирование зазора трибосопряжения непосредственно в процессе эксплуатации подшипника, а также ряда особенностей этого процесса.

Методика исследований. Установка для исследования процесса статической ползучести покрытия (рис.1) имеет винтовое нагружающее устройство с источником усилия в виде образцового динамометра сжатия ДОСМ–3–1; электронагревательный блок, температура которого регулируется хромель-копелевой термопарой и вольтметром марки МР64–02 со специальным устройством, релейно-контактный блок и собственно нагреватель, запитанный через лабораторный трансформатор.

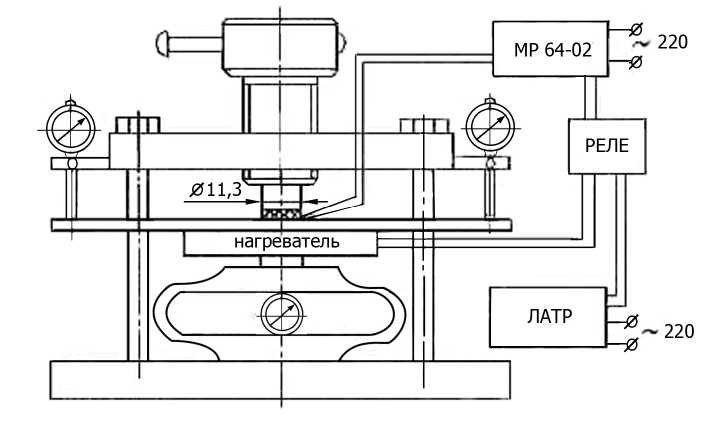
Рис.1. Схема установки для исследования ползучести

Измерение деформаций осуществлялось рычажной системой с двумя индикаторными головками типа ИГ с ценой деления 0,001 мм (ход 1 мм). Во избежание влияния перекосов измерения проводились с двух сторон рычага и за искомую величину деформации принимался средний результат. При этом учитывался знак перемещений. Выполнялось не менее трех параллельных измерений. На первом этапе определялась ползучесть композита при нагружении между плоски- ми поверхностями, на втором – между цилиндрическими поверхностями, соответствующими условиям работы реального подшипника.

Образцы представляли собой полувтулки Ǿ14×10 с покрытием. Армирующая компонента, определяющая композиционную структуру покрытия, выполнялась на основе специальных технических тканей саржевого и атласного плетения, толщиной 0,24 – 0,55 мм. Диапазон варьирования переменных составлял: для напряжений 4,9 - 98,1 МПа, для температуры 294 - 474 ■ 10-2 К.

Анализ полученных результатов. Используя методику двойной параметризации [2], были получены модели первого уровня общего вида:

^(t ) = — +

E 0

—

—

—

к E-  E о 7

1 — e

^— Т

,

к

где — - действующие напряжения, МПа; E о и E _го - соответственно мгновенный и равновесный модули композита при сжатии, МПа; t – время, мин; τ – постоянная времени ползучести, мин.

Параметрическая идентификация моделей типа (1) для исследуемых материалов, выполненная на основе экспериментальных исследований, позволила получить регрессионные модели второго порядка:

E о , E _ю , т = a ■ b ^— T 2 ■ — ^{— dT} 2 ,                         (2)

где a , b , c , d – параметры модели; T – температура, 10^-2 К.

Параметры полученных моделей сведены в табл. 1, а графики зависимостей (2) представлены на рис.2 а, б .

Таблица 1 Примеры параметров моделей ползучести покрытий

Армирующая компонента композита	Толщина покрытия, мм	Тип пуансона	Параметры модели (1)	Параметры модели (2)
				а	b	с	d
Шестиремизный неправильный атлас	0,47	Цилиндр	Е 0	12,830	1,021	0,778	0,010
			Е ∞	9,833	1,003	0,869	0,019
			τ	5,983	0,950	0,103	0,009
	0,31	Цилиндр	Е 0	5,205	0,998	0,987	0,019
			Е ∞	4,959	0,994	0,982	0,021
			τ	7,792	0,965	0,118	--
Саржа 1/1 с 66,9% ПТФЭ	0,29	Плоскость	Е 0	4,385	1,001	1,097	0,016
			Е ∞	3,565	0,986	1,142	0,022
			τ	15,949	0,965	0,248	--

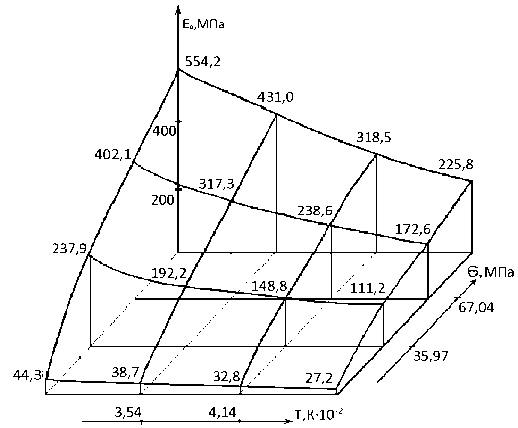
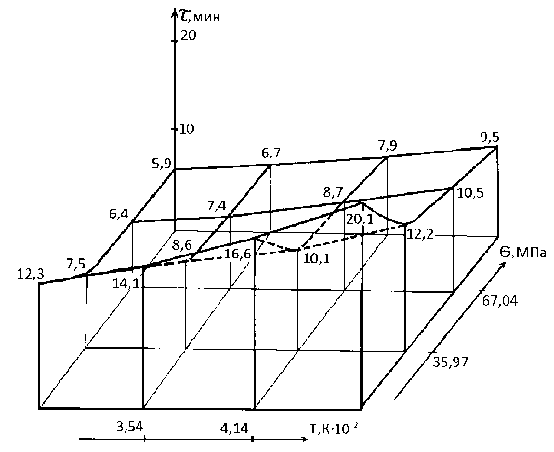
а)                                               б)

Рис. 2. Зависимость мгновенного модуля ( а ) и постоянной времени ползучести ( б ) от термосилового нагружения (саржа 1/1 с 66,9% ПТФЭ)

Следует отметить, что напряжённо-деформированное состояние вязкоупругого покрытия существенно различается при нагружении между плоскими поверхностями и цилиндрическими, имеющими место в подшипнике скольжения. Наибольшую практическую значимость имеет последний тип нагружения, так как в этом случае деформация непосредственно увеличивает зазор в подшипнике.

Геометрические ограничения при смещении коаксиальных цилиндров (вал-втулка) и характер эпюры контактных напряжений в зоне трения подшипника скольжения приводят к неравномерной деформации ползучести. Для ее оценки было выбрано смещение центра вала или его диаметрального сечения в вертикальной плоскости. В качестве характеристики типа нагружения (плоская или цилиндрическая контактная поверхность) предложен параметр К ТН , равный отношению абсолютных деформаций при разных типах нагружения.

Результаты сравнительных экспериментальных исследований ползучести приведены в табл. 2.

Таблица 2

Абсолютная вязкоупругая деформация покрытий на основе саржи, мм

Тип	Контактные напряжения, МПа
	4,9	20,4	35,9	51,4	66,9	82,9	98,1
нагружения	Параметр К ТН
	1,338	1,705	1,790	1,891	1,965	2,046	2,102
Плоский	0,071	0,078	0,081	0,083	0,086	0,087	0,088
Цилиндрический	0,095	0,133	0,145	0,157	0,169	0,178	0,185

По данным табл. 2 построена адекватная эмпирическая модель зависимости параметра К ТН от контактных напряжений:

К ТН = 1,075 ст 0,15 .

Перемещение вала в подшипнике с композиционным покрытием может быть определено как произведение выражений (1) и (3) с учётом исходной толщины покрытия H :

5 ( t ) = 1,075 • H • ^ 1,¹⁵

--+

E 0

V E да

—

E

A

• 1 — e

—

t A

т

,

0 7

V

где δ – абсолютная деформация покрытия в диаметральном сечении сопряжения подшипник-вал, мм.

Анализ полученных моделей и графиков показывает, что зависимости модулей E 0 и E _х от термосилового нагружения носят аналогичный характер, так как модели аналогичны по структуре, а их параметры близки по величине. Температура, пластифицируя матрицу, уменьшает жёсткость покрытия, а напряжения, затрудняя подвижность сегментов макромолекул, повышает её. Это характерно для всех антифрикционных покрытий данного класса [2].

В исследованном диапазоне нагружения величина контактных напряжений сжатия влияет на покрытия существенно интенсивнее температуры. Подобный факт может быть объяснён распределением фторопластовых волокон в армирующей композит ткани и полным отсутствием адгезии матричного связующего к фторопласту, что заставляет относительно легко деформировать аморфную матрицу.

Противоположное влияние напряжений и температуры приводит к экстремальной (min) зависимости постоянной времени ползучести от этих параметров (см. рис. 2, б ). Напряжения определяют величину вязкоупругой деформации в начальный период нагружения, а температура – общую продолжительность процесса.

Существенный интерес представляет соотношение мгновенного и равновесного модулей покрытия, которое может быть использовано для оценки упругой и вязкой составляющих деформации при формировании зазора в трибосопряжении.

Это соотношение для исследованного покрытия на основе саржи 1/1 с 66,9% политетроф-торэтиленовых волокон будет:

EL- - 1,230-1,013-T2 а°,°06T2 -0,045, (5) E „ для покрытий на основе неправильного атласа толщиной 0,55 мм:

E ^ - 1,305 - 1,017 — ^{T 2}

E »

^ 0,01 T ² - 0,09

Следует отметить, что структура выражений (5) - (6) свидетельствует о наличии зоны поверхности отклика, где выход не зависит от параметров модели, поскольку влияние температуры и напряжений противоположно.

Особый интерес представляет задача для этих зависимостей, заключающаяся в отыскании области изменения значений параметров T и σ , которые обеспечат равенство этого отношения единице. Подобный факт равенства модулей E 0 = E _го в исследованном диапазоне факторного пространства может существенно упростить инженерные расчёты.

Для нахождения этой области формализуем задачу, введя буквенные обозначения числовых параметров, входящих в (5) и (6):

7 - T2 cT2 -di а -1,

<при оф...^    ],

T ^ [ T min , T max ] .

Логарифмируя уравнение (7), получаем:

[c In(а)- In(b)T2 - [d In(а)- ln(a)] - 0 ^ T(а) - dLn^pLLZn^pn.(8)

\ c In ( а ) - ln ( b )

Здесь решение уравнения (7) представлено в виде функции от параметра σ , что позволяет, изменяя σ внутри исследованного диапазона, получить все соответствующие значения температуры. То обстоятельство, что выражение, стоящее под квадратным корнем, должно быть неотрицательным, накладывает дополнительные ограничения на допустимые значения напряжений σ .

Вещественные значения температуры могут быть получены при
	d In ( о ) - In ( a ) >  0 c In ( о ) - In ( b ) >  0	о >  exp о >  exp	( In ( a )/ d ) ( ln ( b У c )	(9)
> о >  max ' exp ( ln ( a ) [d ) ,exp (			ln ( Ь )/ c ) ] = о 2 ,
1	d In ( о ) - In ( a ) <  0 c ln (о)- ln ( b ) < 0	о <  exp ^о <  exp	ln ( a )/ d ) ln ( b V c )	(10)
> о <  min ' exp ( In ( a )/ d ) ,exp ( l			n ( b V c ) ] = ° i -

Как видно из выражения (8), зависимость температуры от напряжений, при которой удовлетворяется (7), нелинейная.

Зона равенства модулей в реально исследованном и достижимом диапазоне температур и контактных напряжений существует только у относительно толстого покрытия (0,53 – 0,56 мм), сформированного на основе неправильного атласа.

В общем случае, но особенно для этого материала, представляет интерес поведение корней уравнения (7) при совместном изменении температуры и контактных напряжений. Чтобы выяснить это, левая и правая части уравнения (7) были протабулированы в области реально исследованных изменений переменных факторов и представлены в виде графиков на рис.3.

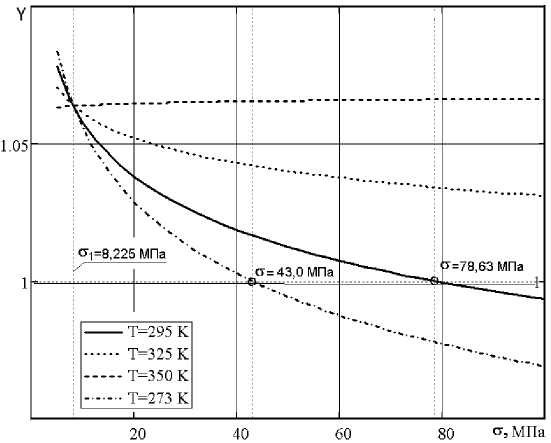
Рис. 3. Точки пересечения линий семейства корней уравнения (7) и прямой Y = 1 , обеспечивающие равенство модулей

Для большей наглядности на графике приведено семейство кривых, представляющих левую часть уравнения (7) при различных температурах. Точка пересечения линии при T = 295 К с горизонтальной прямой Y = 1 дает величину напряжения, соответствующего температуре, при которой модули E о и E _го равны. Интересно отметить, что все кривые семейства пересекаются в точке, соответствующей ранее определенному напряжению.

Выводы. Экспериментальные исследования вязкоупругого поведения антифрикционных композиционных покрытий позволили установить, что деформация ползучести достигает 18,5%, что составляет значительную долю рабочего зазора подшипника. Кроме того, установлены основные закономерности протекания этого процесса в покрытиях разной структуры. Впервые получены регрессионные модели, описывающие ползучесть непосредственно в самом подшипнике, и позволяющие выявить особенности противоположного влияния на вязкоупругую деформацию нагрузки и температуры, вызывающую эффект равенства мгновенных и равновесных модулей полимерного покрытия.