Исследование поперечно-модового состава бездисперсионных многомодовых пучков с помощью корреляционных фильтров

Фундаментальными свойствами мод являются свойства сохранения поперечной амплитудно-фазовой структуры отдельных мод и взаимной ортогональности при распространении в соответствующих волноводных средах (например, в свободном пространстве или волноводе) [1-3]. В работах [3, 4] рассмотрены МОДАНы – дифракционные оптические элементы, позволяющие формировать и селектировать моды лазерного излучения. Как будет показано ниже, двумерный характер сечения реальных волноводов допускает существование пучков, амплитудно-фазовое распределение в поперечном сечении которых описывается суперпозицией нескольких мод, обладающих одинаковым значением постоянной распространения. Такие пучки ранее были названы «бездисперсионными» [1] из-за их способности распространяться с нулевой межмодовой дисперсией. В данной статье ограничимся рассмотрением Гауссовых мод, характерных для градиентных волокон с параболическим профилем.

Основной формализм

Для градиентного волоконного световода с поперечно-неоднородным показателем преломления n( x ) волновые фронты направляемых мод являются плоскими [2]. В этом случае оператор распространения P связывает решение F( x ,z) уравнения Гельмгольца

• , , x d2 F (x, z)

• V_± F ( x ,z ) + -2---’- + n ( x ) kF ( x , z ) = 0    (1)

о z с граничным значением комплексной амплитуды F|z=0 = F(x,0), где VL=(8/8x, 8/8y) - поперечный дифференциальный оператор Гамильтона (рис. 1).

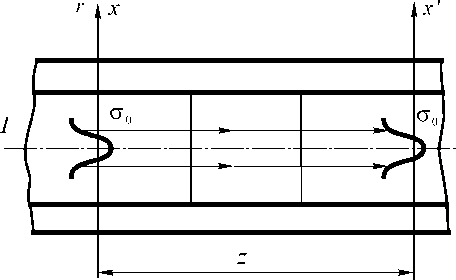
Рис. 1. Распространение мод в градиентном волокне

При учете конечного диаметра волновода появятся дополнительные граничные условия на границе сердечника. Моды градиентного волокна имеют плоский волновой фронт и удовлетворяют уравнению [3]

V vp (x)+[k 2 n 2 (x)- в 2p ] Vp (x) = 0.

Для произвольного значения z имеем

F(x,z) = Yp Vp(x),

Yp = exp(Kpz), kp = Pp +1qp,(5)

где p p — константа распространения, q _p — коэффициент затухания моды y p , p = ( p,l ) .

В [3] показано, что в случае параболического профиля

,           , С       X2² + у 2)

n ² ( x,y ) = n 1 1 - 2A----

где a – радиус сердечника волокна,

Y p ( z ) = exp ( i p p z )

где

P p =

k^{2 n} 2^- ~p ⁽ r p ^{+ 1 )}

Исследование поперечной амплитудно-фазовой структуры бездисперсионных пучков

Для исследований фундаментальных свойств бездисперсионных многомодовых пучков был изготовлен МОДАН, предназначенный для преобразования гауссова пучка с поперечным распределением интенсивности в плоскости установки ДОЭ

I 0 ⁽ X , у ) = exp

2 ( x² + у² )

^с 00

и постоянной фазой в сумму мод Гаусса-Эрмита с номерами (4,0) и (2,2) с единичными весами:

Х 4 ( ^x ) = Е C ^ i ^( 4 - i ) ( ^x ) ,                        ⁽¹⁶⁾

i = 0

k - волновое число, с - радиус основной моды, r p = r p ⁽ P,l ) .

Решения уравнения (2) в этом случае могут быть записаны через полиномы Эрмита [3]:

I 1, i = 4

C i =<| 1, i = 2 .

1 0, иначе

E pl

C n2 ^{p + l} p ! I ! ’

С

V p ( x ) = E pi H p\ — I H

где H_p ( ■) — полином Эрмита p- го порядка.

Причем [3], rp = P +1.                                        (10)

Отметим интересную особенность пучков, состоящих из гауссовых мод с одинаковым значением постоянной распространения β _P . Комплексная амплитуда в сечение таких пучков имеет следующий вид:

r p

X r p ^{( x ) =} E C W^-o ^{( x )} .                    ⁽¹¹⁾

i = 0

Распространение пучков вида (11) будет напоминать распространение отдельных мод ψ p ( x ). В самом деле, пучок когерентного света с поперечным сечением вида (11) будет обладать свойством самовоспроизведения амплитудно-фазовой структуры в ходе распространения в соответствующей среде. Пучки такого вида называют инвариантными модовыми пакетами (точнее, они являются разновидностью инвариантных модовых пакетов, о которых подробнее можно прочитать в [5]) или многомодовыми бездисперсионными импульсами .

Подобно отдельным гауссовым модам, пучки вида (11) не изменяют своей амплитудно-фазовой структуры при распространении в линзоподобных средах, свободном пространстве, при прохождении через Фурье-каскад, изменяя лишь фундаментальный модовый радиус.

Таким образом, функция комплексного пропускания изготовленного ДОЭ может быть записана в виде:

T ^{( x} , У ) =

X 4 ( ^x , У ) V I 0 ( ^x , У )

На рис. 2 и 3 представлены, соответственно, рассчитанные амплитудное распределение в сечении пучка \/ (Xx , у )| и фазовое arg ( ^ 4 ( x , у ) ) .

Рис. 2. Теоретическая оценка амплитудного распределения в сечении бездисперсионного пучка

Амплитудно-фазовая функция пропускания элемента кодировалась в чисто фазовую с помощью введения прямоугольно-импульсной несущей 33,3 линий/мм в фазу элемента (обобщенный метод Кирка-Джонса, [3]). Маска элемента имела 1024*1024 пиксела, размер одного пиксела 3 мкм.

Рис. 3. Теоретическая оценка фазового распределения в сечении бездисперсионного пучка (черный цвет соответствует нулевому значению фазы, белый цвет соответствует значению фазы π )

Элемент рассчитывался как добавка к внешней Фурье-линзе для следующих физических параметров: длина волны освещающего пучка λ =632,8 нм, радиус освещающего гауссова пучка σ 00 =0,525 мм, фундаментальный радиус мод в формируемом без-дисперсионном пучке σ = 0,5 мм, фокусное расстояние линзы f ₁= 452 мм.

Рассчитанный элемент был изготовлен путем многоуровневой электронно-лучевой прямой записи в резисте ПММА с последующей химической обработкой. Исследование способности изготовленного элемента формировать бездисперсионный пучок проверялось с помощью серии натурных экспериментов. Экспериментальная установка, представленная на рис. 4, использовалась для измерения интенсивности в фокусе Фурье-линзы. Типичный результат представлен на рис. 5.

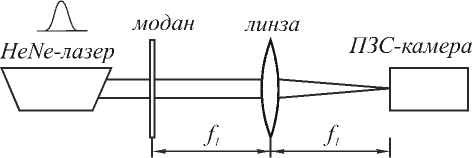
Рис.4. Экспериментальная установка для исследования МОДАНа

Сравнительный анализ теоретических оценок с экспериментальными результатами (рис. 2 и 5) демонстрирует хорошее взаимное соответствие.

Для экспериментального подтверждения «инвариантного» характера сформированного пучка исследовалась устойчивость амплитудно-фазовой структуры к оптическому аналогу Фурье-преобразования. Комплексная амплитуда в сечении бездисперсионного пучка должна сохранять свою структуру при прохождении через Фурье-каскад.

Рис. 5. Амплитуда как результат измерения интенсивности в выходной плоскости МОДАНа

Схема экспериментальной установки, использовавшейся в данном эксперименте, представлена на рис. 6. Типичное распределение, полученное в ходе эксперимента, представлено на рис. 7.

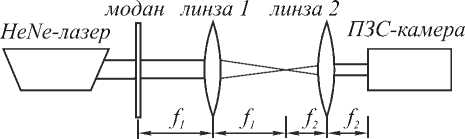
Рис. 6. Схема экспериментальной установки для исследования прохождения бездисперсионного пучка через Фурье-каскад

Рис. 7. Амплитудное распределение в сечении бездисперсионного пучка как результат измерения интенсивности в фокальной плоскости линзы 2

По результатам измерений интенсивности в ближней и дальней зонах восстанавливалась фаза пучка. Фаза восстанавливалась в ходе 26 итераций хорошо известного итерационного алгоритма Фье-напа [6].

После завершения 26 итерации, среднеквадратичное отклонение оценки амплитуды от амплитуды, восстановленной по результатам измерения интенсивности, было менее 16%. Восстановленные фа- зовые распределения во входной и выходной плоскостях Фурье-каскада представлены на рис. 8.

а)                          б)

Рис. 8. Результаты восстановления фазы бездисперсионного многомодового пучка по результатам измерения интенсивности a) оценка фаза пучка в ближней зоне, b) оценка фаза пучка в дальней зоне

Таким образом, устойчивость сформированного двухмодового бездисперсионного пучка к прохождению через Фурье-каскад, была исследована методом оптического эксперимента и результаты находятся в хорошем соответствии с теоретическими результатами.

Исследование поперечной модовой структуры бездисперсионных пучков

В качестве верификации результатов исследования поперечной амплитудно-фазовой структуры в данной работе проводилось исследование поперечномодового спектра, сформированного бездисперсионно-го пучка. Измерение поперечно-модовой структуры пучка было решено произвести с помощью МОДАНа – корреляционного фильтра, согласованного с модами лазерного излучения . Удобнее всего реализовать такой МОДАН в виде амплитудной бинарной голограммы, соответствующей комплексной функции mod

T ( x ) = ∑ ψ _n ^∗ ( x ) exp( i 2 π ν_nx ),               (16)

n = 0

где x =(x, y), νn = (νnx ,νny ) - вектор, определяющий координаты центра дифракционного порядка, соответствующего модовой функции ψn (x). В [3] показано, что корреляционные пики, амплитуда которых пропорциональна содержанию в пучке соответствующей моды будут наблюдаться в выходной плоскости Фурье-каскада в точках с координатами xn=vnλf. Соответствующий МОДАН для мод Гаусса-Эрмита низших порядков был реализован в виде бинарной амплитудной голограммы по методу Ли с числом ячеек 512 × 512 по технологии электронной микролитографии. В нашем случае выбиралось Nmod=16. Измерялось содержание мод Гаусса-Эрмита со следующими порядковыми номерами: (0,0), (0,1), (1,0), (2,0), (0,2), (1,1), (3,0), (0,3), (1,2), (2,1), (4,0), (0,4), (1,3), (3,1), (2,2), (0,5).

Для исследования поперечно-модового состава сформированного бездисперсионного многомодового пучка была собрана схема, представленная на рис. 9.

Модан 1 – фазовый дифракционный элемент, формирующий пучок, состоящий из мод Гаусса-Эрмита с номерами (4,0) и (2,2). Модан 2 – амплитудный оптический элемент с функцией пропускания (16). Линза 1 имела фокусное расстояние f 1 =452 мм, линза 2 – f 2 =300 мм. Расстояния z 1 , z 2 , z 3 , z 4 выбирались, исходя из значений f 1 , f 2 .

На рис. 10 представлено корреляционное поле модана 2 при освещении модана 1 пучком лазера. На рис. 11 представлено замеренное распределение интенсивности в центрах корреляционных пиков, соответствующих различным модам Гаусса-Эрмита, в выходной плоскости анализирующего элемента.

Измерение интенсивности в центрах корреляционных пиков, соответствующих различным модам лазерного излучения, показало (как видно из таблицы 1), что значение интенсивности в центрах пиков, соответствующих модам (2,2) и (4,0), минимум в 9,5 раз превышает значение интенсивности, замеренное в центрах корреляционных пиков нерасчетных мод.

Именно высокое содержание таким образом заданных мод с одинаковым значением постоянной распространения и определяет «инвариантный» характер исследованного пучка, продемонстрированный в ходе исследования устойчивости амплитудно-фазовой структуры к преобразованию Фурье (рис. 2-рис. 8).

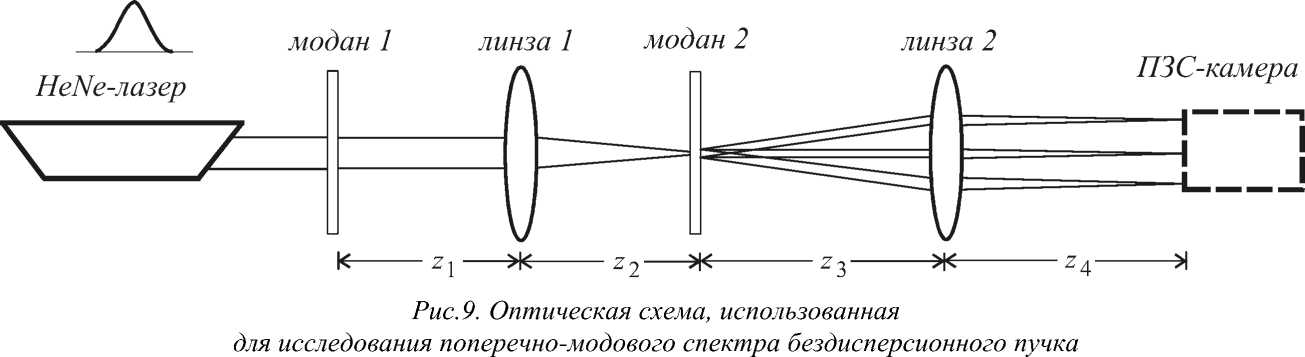
Рис. 10. Распределение интенсивности в корреляционной плоскости анализирующего модана

Таблица 1

(4,0) 74,5%	(2,0) 3,7%	(0,4) 1,6%	(3,1) 2,5%
(1,0)	(0,1)	(0,0)	(1,3)
5,8%	0,4%	3,3%	0%
(0,2)	(5,0)	(1,1)	(2,2)
2,5%	3,3%	1,2%	77,8%
(3,0)	(2,1)	(1,2)	(0,3)
7,8%	0%	7%	0%

Замеренное распределение интенсивности в центрах корреляционных пиков, соответствующих различным модам Гаусса-Эрмита, в выходной плоскости анализирующего элемента (в круглых скобках – порядковые номера мод, рядом, замеренная интенсивность в центре корреляционного пика в процентах от максимального замеренного значения интенсивности в выходной плоскости)

Заключение

Таким образом, результаты измерения амплитудно-фазовой структуры бездисперсионного многомодового пучка, сформированного фазовым дифракционным оптическим элементом, находятся в хорошем соответствии с результатами компьютерного моделирования и результатами измерения поперечномодовой структуры пучка, что подтверждает перспективность формирования бездисперсионных многомодовых пучков с помощью фазовых дифракционных оптических элементов.