Исследование поперечных смещений трубной заготовки в процессе её механической обработки на основе компьютерного моделирования

На Таганрогском металлургическом заводе (ОАО «ТАГМЕТ») получение резьбы с требуемыми параметрами затруднено по ряду причин. В процессе нарезания в системе СПИД заготовка вращается и прогибается под собственным весом. Всё это вызывает колебания. Изменяются силы резания. На рассматриваемом участке основными видами резьбы являются ОТТМ, ОТТГ, БАТ-ТРЕСС. Диапазон диаметров труб — от 140,0 мм до 219,0 мм. Толщина стенок — от 7,0 мм до 12,1 мм. Длина труб — от 8,5 м до 12,3 м.

Целью проведённого исследования является повышение качества резьбы на обсадных трубах путём уменьшения амплитуд автоколебаний, возникающих в системе СПИД.

Описание предлагаемой модели. Трубную заготовку для простоты можно рассматривать как тонкий, упругий стержень с равномерно распределённой массой.

Чтобы учесть влияние кривизны заготовки на возникающие в системе колебания, введём параметр кривизны, учитывающий геометрические особенности реальной заготовки.

На рис. 1 переходные матрицы 3-го, 7-го, 8-го участков обозначены соответственно Q3×H3, Q7×H7, H8; длины 1-го, 2-го и 8-го участков — соответственно l1, l2, l8; величины поперечных прогибов в сечениях 0, I, II, VI, VII и VIII — z0, z1, z2, z6, z7, z8; величины угла поворота в сечениях 0, I, II, VI, VII и VIII — φ0, φ1, φ2, φ6, φ7, φ8; EJ — крутильная жёсткость стержня; h, k — соответственно коэффициент демпфирования и жёсткость шпинделя; F — сила резания; ρF — масса единицы длины стержня.

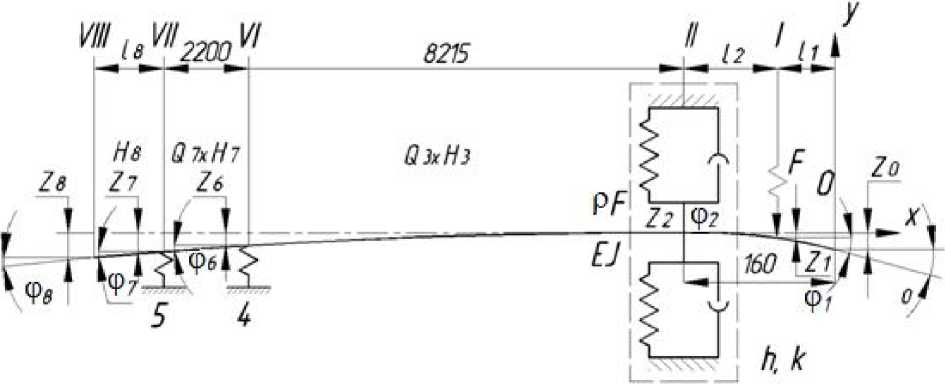
Рис. 1. Схема деформации трубной заготовки с двумя опорами

Для удобства определения параметра кривизны принимаем, что труба имеет форму дуги, принадлежащей некоторой окружности радиуса r. Тогда величина прогиба определяется как кратчайшее расстояние от вершины дуги до её хорды.

Для расчёта величина прогиба трубы под собственным весом была принята равной l пр = 4 ∙ 10^-3 м. Радиус кривизны определяется из соотношения:

r =

^P ⁺ ( ^L )

2л

Прогиб в z -м сечении легко определить по формуле:

( z                I )'

^z Pr =1 r 2 -I t " k +5\

V k = 0         ² )

—

—

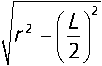
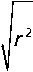
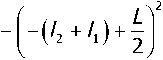
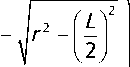
где zprz — прогиб стержня в z-м сечении; lk — длина стержня k-го участка; L — длина всего стержня.

Начальный угол прогиба для рассматриваемых сечений будет определяться как

φ pr_z

π

* 2 — arctg

r ^— ( / пр ^— zpr z ) L — ( t k = / k )

где φ pr z — угол прогиба стержня в z -м сечении.

Для нахождения смещений трубной заготовки во время процесса обработки удобно воспользоваться методом начальных параметров [3], [4]. Переходная матрица участка будет иметь вид:

( Az Bz Cz DzЛ 4 A В C Hk = zz A 'Cz z λz4Dz z Az z Bz ,                                         (4) V A k Bk λz4Cz λz4Dz Az) где Az, Bz, Cz, Dz — функции А. Н. Крылова для z-го участка стержня.

Матрица H z учитывает свойства материала и его геометрию, но для вычисления характеристик в соседнем сечении необходимо также учесть характеристики опор, на которых располагается заготовка. Это можно сделать переходной матрицей Q z :

Q z =

Г 1

V ° z

0 ^х 7

f

V ■ 1 ³

где e = —z — смещение люнета под воздействием заготовки.

^z E ■ J

В нашей модели заготовка совершает вращательное движение, поэтому необходимо учесть влияние инерционной силы. Можно сделать это при помощи матрицы Kz:

K z

1 δ z

f

I ■ l z

где 5 _z =— ^V e j0 ---— смещение под действием инерционной силы; J_z = m_z

D 0 + d

- + m z zpr z —

момент инерции трубы в z -м сечении вдоль оси ОХ , zpr z = 0

—

для

данной модели;

D 0 2 + dd

J 0 = ms --— момент инерции трубы вдоль оси ОХ .

резания, вводим

Чтобы учесть воздействие на систему радиальной составляющей силы матрицу F_i :

_ Г             _ /23 1

F i = 0 0 0 P ■ -^- ,                                 (7)

V                  E ■ J 7

где l 2 i — длина 2-го участка в i -й момент времени.

Для применения метода начальных параметров необходимо знать начальные условия одного из концов стержня. В нашей модели сечение № 2 представляет собой зажим в патроне станка, деформациями которого мы пренебрегаем ввиду большой жёсткости подшипниковых опор шпинделя. То есть для любого момента времени угол, на который отклоняется заготовка от своей оси, и координата её поперечного смещения вдоль оси Z равны нулю:

Ф 2, i = ⁰, Z 2, i = ⁰

Тогда получаем систему уравнений в матричном виде:

(Z Л Z2,' (z Л Z0,' Ф2, i = K 2 i ■ H2 i ■ K1i ■ H1i ■ Ф0, i + K2,. ■ H2,. ■ F ,                               (8) 0 0 i                  i i о V 0 7 V 0 7 где K1i , K2i — переходные матрицы, учитывающие инерционные силы в i-й момент для 1-го и 2-го участков соответственно; H1i , H2i — переходные матрицы в i-й момент для 1-го и 2-го участков соответственно.

Решение системы уравнений (8) будет иметь вид:

Z = Д2 i .      =    А1 _;

.

⁰ i Д0 i ' ^Ф0 i Д0 i ■ 1 2 i

Здесь

Д0 i =	( Z _1 i ) 0,0   ( Z _1 - ) 0,1 ( Z _! ) 1,0   ( Z _! ) 1,1	;	(10)
A1 i =	( Z _1 - ) 0,0 — ( O 1 . 1, , ( Z _! ) 1,0 — ( O _! ) 1,0	.	(11)
Z 1,. = K 2,. ■ H 2 ii	■ K 1. ■ H 1,.; O 1. = K 2,. ■ H 2, ■ F ; i     i     i        i      i     ii		(12)
Д2 - =	— ( O _1 i ) 0,0   ( Z _1 i ) 0,1 — ( O _1 i ) 1,0    ( Z _1 i ) 1,1	.	(13)

T

^M 1, i + F i ^.

0 ) , M^ = K1 i ■ H1 i ■ Z 00 Ti . N ii

Обозначим

Z 00 i = ( Z 0, Фо, 0

Тогда

Z 1,i = ( N 1, i ) oo

—

zpr 1 i , Ф 1, i = ( N 1, i ) ₀₀ ■ lv ^— ф р^г1 - ,

где zpr 1 _i и φ pr 1 _i — величины поперечного и углового смещения 1-го участка в i -й момент времени. Для нашей модели они приравниваются нулю.

Зная начальные условия в 0-м сечении, можно определить смещение детали в различных сечениях. Для этого необходимо последовательно перемножить переходные матрицы участков, в которые входят соответственно матрицы, учитывающие жёсткости опор, инерционные характеристики, геометрические характеристики сечения.

Введём следующие обозначения:

z

O zi = П ( MQ z • K z • H z ) ■ K 2 i • H2 i • F T , k = 3

z

M z,i = П ( MQ z • K z • H z ) ■ K2 i • H 2 i • M 1,i , k = 3

N z , i = O z , i + M z , i .

Отсюда

I               f z.

^Z z , i = ( N zi L — zpr z . Ф z, = ( ^N z , i ) o1 ■ I ^{l 1} i + 1 2 - + I Tlz

V              V k = 3

— 1

—

φ pr_z ,

где z = 0 … 26 — номер рассматриваемого сечения, i = 0 … 80 — момент времени.

Решение уравнения движения участка стержня в проекции на плоскость ZОX будет иметь следующий вид:

_         _ I to ■ 2 ■ П ■ t.

.

ZY, i = Z, i ■ sin ----------L + Ф7 i z.i        z.i         I 60           ^z, i

Чтобы определить траекторию движения оси симметрии трубной заготовки в различных сечениях, необходимо найти проекции этих смещений (для дальнейшего нахождения результирующей). В нашем случае необходимое и достаточное количество таких проекций — две, в плоскостях ZОX и YОX .

В плоскости YОX на стержень будут действовать те же силы, что и в плоскости ZОX (в данном случае весом трубы мы пренебрегаем). Следовательно, переходные матрицы останутся неизменными. Проекция радиальной составляющей силы резания на плоскость YОX будет равна:

P 1 = P .

В горизонтальной плоскости жёсткость опор будет определяться зависимостью tYz = viz

2 • E • J

Матрица жёсткости примет следующий вид:

( 1

QY , =

V

-e Y _z

0 0 0 )

1 0 0 0 1 0

0 0 1 ,

Матрица, учитывающая воздействие радиальной составляющей силы резания в проекции на плоскость YОX , выглядит как:

F 2 , = 1 0 0 0 P 1 •

1 2 / f E • J I

.

Матричное уравнение движения стержня в плоскости YОX и его решение будут иметь такой же вид, что и в плоскости ZОX, с разницей лишь в самих переходных матрицах, матрицах, учитывающих влияние жёсткости опор, а также в матрице, учитывающей воздействие режущего инстру- мента на заготовку.

Зная решения уравнений движения в двух проекциях, можно определить траекторию движения стержня (по сути, оси стержня) в пространстве [5].

Если рассматривать отдельно взятые сечения в плоскости ZОY, то можно представить тра- екторию вращения оси стержня в виде эллипса с осями, равными YYi,l, ZYi,l.

Уравнение эллипса можно представить в виде:

(

" ( y , z , i ) = . 1 - Yyr • ZYi ., .

V          z , i I

Анализ полученных результатов. На момент проведения эксперимента на рассматриваемом участке окончательной отделки работали лишь два крайних люнета — № 4 и № 5 (см. рис. 1). Естественно одной из наших задач было выяснить, как этот факт отразится на качестве получаемой резьбы.

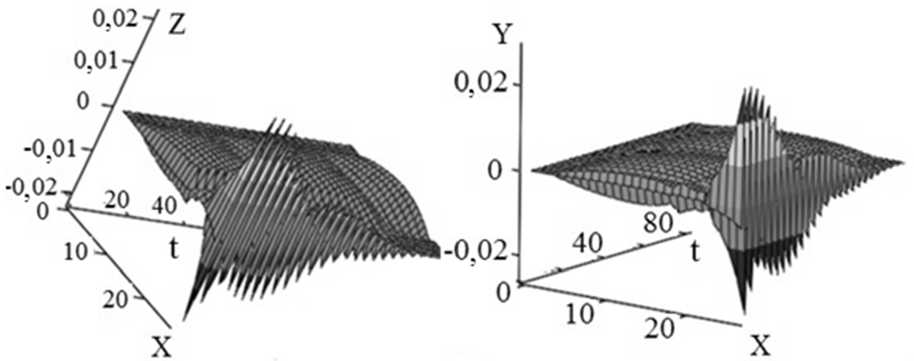
На рис. 2, а , б на оси X отображена координата поперечного сечения стержня, на осях Z и Y — поперечные смещения стержня соответственно вдоль осей Z и Y , по оси t — время в секундах.

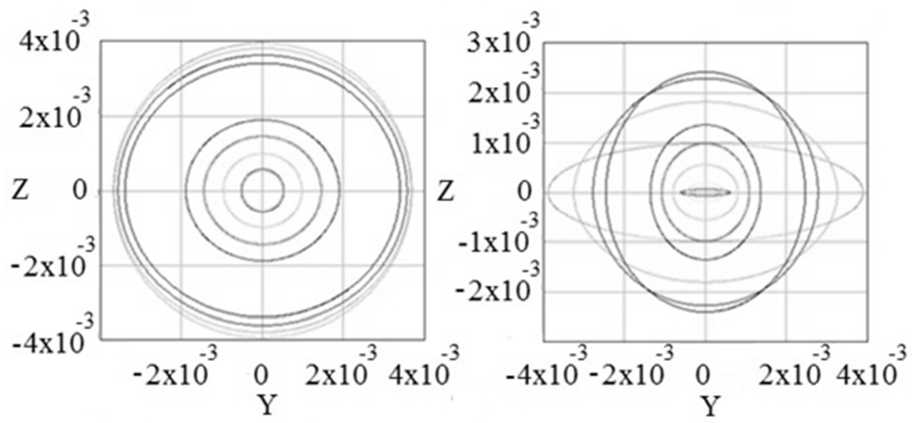
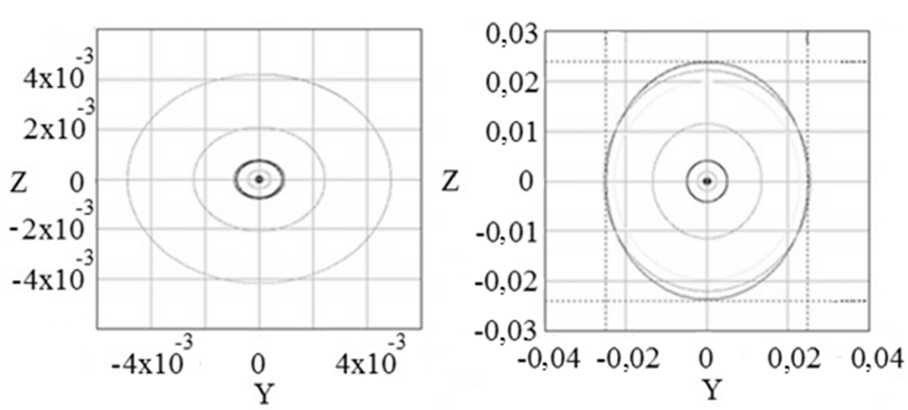
На рис. 2, в , г , д , е — на вертикальной оси изображены поперечные смещения стержня вдоль оси Z , на горизонтальной — вдоль оси Y .

Все линейные размеры на рис. 2 указаны в миллиметрах.

Из рис. 2 видно, что формы колебаний стержня претерпели значительные изменения. После 18-го сечения амплитуда колебаний кардинально меняется. В сечении № 8, ввиду наличия в нем опоры, амплитуда колебаний резко уменьшается, затем наблюдается некоторый её рост до того момента, пока колебания не достигнут 5-й опоры, где значения амплитуды падают до минимальной отметки. После того как колебания достигнут сечений, находящихся за 5-й опорой, наблюдается резкое возрастание амплитуды. В начальные моменты времени в крайних сечениях она принимает значения порядка 20 мм.

В плоскости YОX подобные явления выражены менее ярко, однако амплитуды колебаний в крайнем сечении имеют практически такие же значения, что и в плоскости ZОX .

По результатам проведённых расчётов можно сделать вывод о том, что 5-я опора практически все время подвержена силовым перегрузкам, которые могут привести к её преждевремен- ному выходу из строя.

0.02

0.01

0.01

0.02

4x10

3x10

2x10

1x10

1x10

2x10

4x10

2x10

2x10 4x10

4x10 -2x10

2x10 4x10

0.03

4x10

2x10

0;01

0;01

4x10

4x10

4x10

0.03

" -0-04 -0.02

д )

е )

Рис. 2. Проекция динамических смещений за весь период протачивания на плоскость: а — ZОX , б — YОX ;

смещения в различные моменты времени в сечениях: в — № 14, г — № 18 — 4-й люнет, д — № 22 — 5-й люнет, е — № 26 — свободный конец стержня

Количество опор и их положение влияют на параметры технологической системы, изменяя её собственную частоту колебаний. Поэтому должен быть такой вариант, когда амплитуда колебаний стержня, вызванных прогибом заготовки под собственной массой (а следовательно, и в зоне резания), будет минимальна. Это обеспечит наибольшую точность обработки. Итак, одна из первостепенных задач — нахождение такого количества опор и такого расстояния между ними, при которых выполняется вышеуказанное условие.

В некоторых поперечных сечениях наблюдается смещение осей эллипса на π/ 2 (в дальнейшем данное явление в статье будем называть переходной стадией), особенно ярко выраженное в 4-й опоре (рис. 2, г ). Смещение отрицательно сказывается на качестве резьбы, так как оно сопровождается периодическим увеличением полуоси эллипса в плоскости YОX . В определённые моменты, когда значение полуоси эллипса в плоскости YОX достигает предельных величин, заготовка может на короткое время выскочить из паза люнета, тем самым вызвав ударную нагрузку в системе СПИД. Это явление неоднократно наблюдалось на рассматриваемом участке.

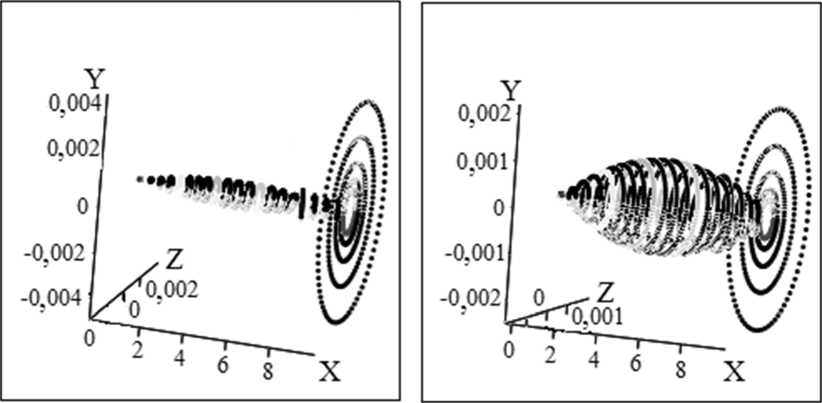
а )                                                    б )

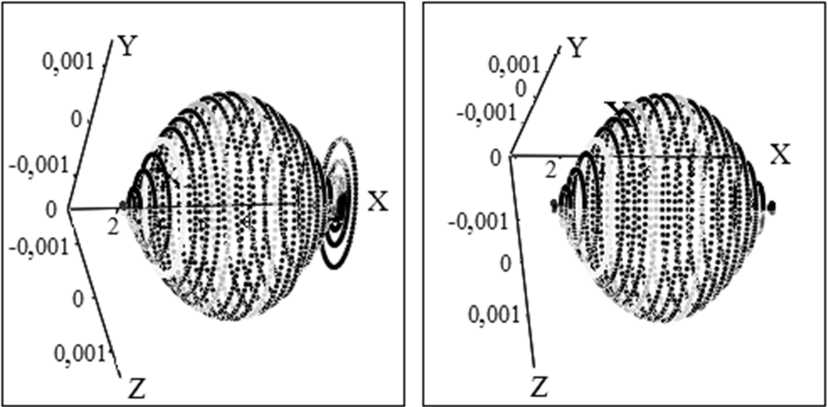
в )                                                            г )

Рис. 3. Траектории движения оси вращения в различных сечениях в фиксированные моменты времени: а — 0 с; б — Т /2 с; в — 3 Т /4 с; г — Т с; Т = 35 с — время одного цикла протачивания; ось X — координата поперечного сечения стержня;

Z и Y — величины поперечного прогиба стержня соответственно вдоль этих осей; все размеры указаны в метрах

Из рис. 2 видно, что сечение 18 выступает в роли своеобразного демпфера: колебания, передаваемые от зоны возбуждения к сечению № 18, распространяются по свободной части заготовки до 4-го люнета, который является первым препятствием на их пути. Пройдя 4-й люнет, колебания через небольшой промежуток времени достигают 5-го люнета (сечение № 22), который также препятствует возникновению переходных стадий. После прохождения 5-го люнета колебания преодолевают оставшееся расстояние так же, как и до 4-го люнета. Поэтому в сечении № 26 (крайнее сечение) мы снова наблюдаем наличие переходных стадий. Таким образом, можно предположить, что при большем количестве опор наличие переходных стадий и, как следствие, возникновение в системе СПИД ударных нагрузок менее вероятно.

Для рассматриваемой модели имеются два сечения (рис. 3), в которых в различные моменты времени достигаются наибольшие отклонения от оси вращения. Первое сечение — координата максимального прогиба заготовки, второе — крайнее сечение свободного конца заготовки. Анализ влияния расположения опор станка на колебания заготовки. Ранее было отмечено, что на амплитуду колебаний поперечных смещений стержня существенное влияние оказывает устройство крепления: количество и расположение между собой люнетов [6].

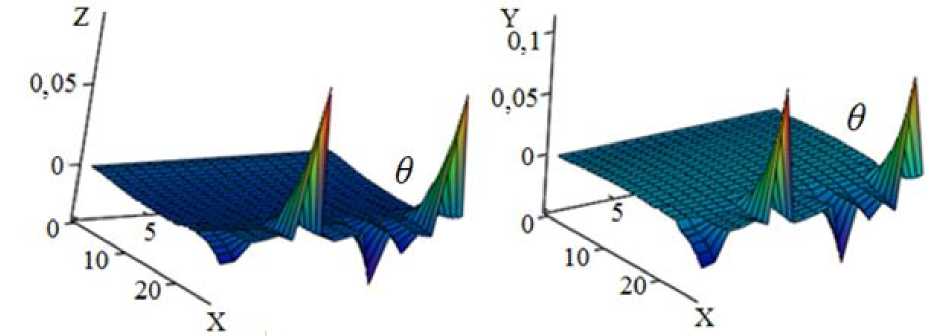
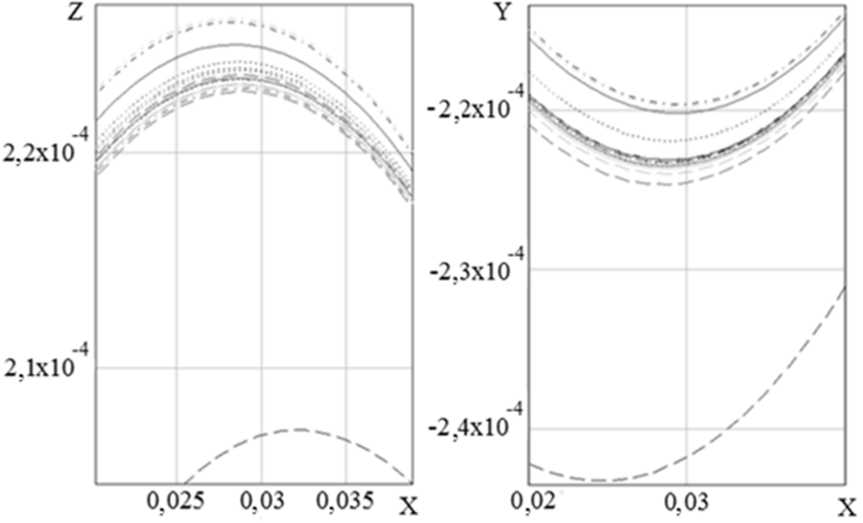
в )

г )

Рис. 4. Изменения амплитуды колебаний стержня: а , в — вдоль оси ОZ и б , г — вдоль оси ОY

На рис. 4, а , б показаны поперечные смещения стержня вдоль осей Z и Y соответственно в зависимости от координаты сечения трубы X и номера схемы расположения опор станка — θ. Все размеры указаны в метрах.

На рис. 4, в , г показаны поперечные смещения стержня в зоне резания вдоль осей Z и Y соответственно. Разными типами линий обозначены различные варианты схем расположения опор. По вертикальной оси отложены поперечные смещения стержня в 10^-1 м, по горизонтальной — координата поперечного сечения стержня в метрах.

Большему числу опор соответствует меньшая вероятность возникновения ударных нагрузок. Это ведёт к повышению точности обработки. С другой стороны, на имеющемся оборудовании сложно установить более пяти опор. Поэтому при выборе варьируемого параметра мы остановились только на взаимном расположении опор с неизменным их количеством, равным пяти [7].

Мы проанализировали 16 вариантов взаимного расположения опор. Результаты проведённых расчётов показаны на рис. 4, а , б . Здесь символ θ указывает на номер схемы расположения опор. Логично было бы предположить, что при меньшей амплитуде колебаний в крайнем сечении (№ 26) минимальная амплитуда будет наблюдаться и в зоне резания. Однако это не так (табл. 1).

Таблица 1

Отклонения заготовки вдоль осей ОZ и ОY в зависимости от схемы расположения опор

№ схемы	Отклонение вдоль оси ОZ , 10-2 мм	Отклонение вдоль оси ОY , 10-2 мм	Отклонение радиус-вектора ρ, 10-2 мм
11, 15	2,265	2,161	3,130
0	2,253	2,202	3,150
1	2,44	2,215	3,153
13, 8	2,243	2,227	3,160
14	2,240	2,227	3,159
2, 3, 5, 9, 12	2,235	2,227	3,155
4	2,232	2,229	3,154
10, 7	2,231	2,238	3,160
6	2,069	2,425	3,187

Проведённый анализ показал, что при схеме расположения опор № 6 амплитуда колебаний имеет минимальные значения в зоне резания, в то время как в крайнем сечении № 26 амплитуда колебаний максимальна. Однако уже на рис. 4, г для оси ОY видно, что при этой же схеме крепления амплитуда колебаний достигает максимальных значений.

С точки зрения минимальной амплитуды колебаний в зоне резания наилучшие схемы расположения опор — № 11 и № 15 с приблизительно равной величиной радиус-вектора р = 3,13 ■ 10 - 2 мм. Их отличия от стандартной 0-й схемы показаны на рис. 5.

Использование обеих схем расположения опор даёт практически одинаковый результат. Поэтому целесообразнее использовать ту из них, которую проще реализовать на практике. В нашем случае это схема № 15, так как при её реализации на производстве необходимо сменить положение лишь двух опор, в то время как использование схемы № 11 предполагает перемещение четырёх опор [8, 9, 10].

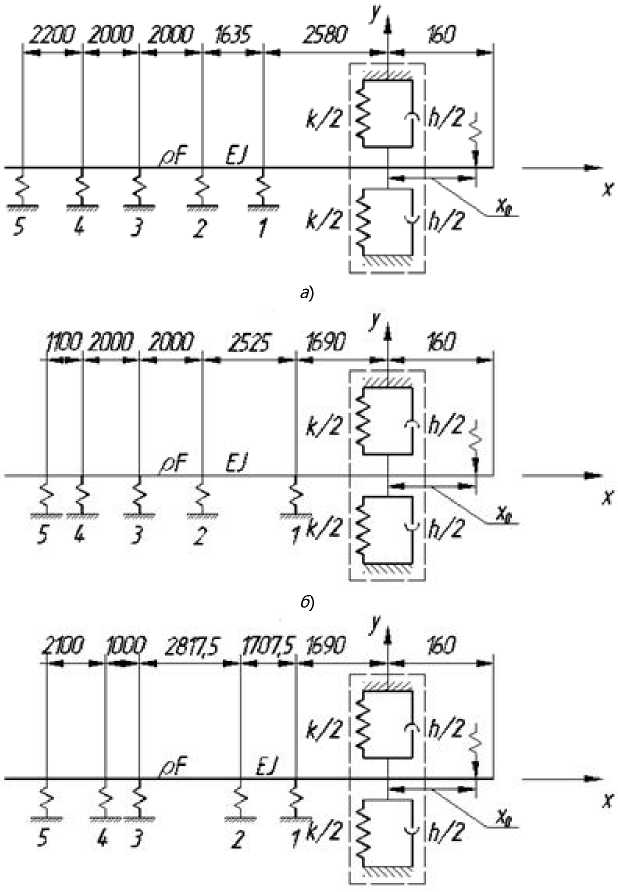
в )

Рис. 5. Схемы расположения опор: а — исходная; б — предлагаемая схема № 15; в — предлагаемая схема № 11

Заключение. В результате проведённой работы из рассмотренных схем крепления заготовки была выбрана наилучшая (по параметру наименьшего отклонения радиус-вектора заготовки). Получены схемы крепления с меньшими величинами отклонений радиус-вектора, чем смещения для исходной схемы. В рассмотренных схемах минимальное отклонение радиус-вектора составило 3,13 ⋅ 10 ^{- 2} мм при исходном 3,15 ⋅ 10 ^{- 2} мм. Это свидетельствует об уменьшении погрешности позиционирования.

В дальнейшем планируется провести оптимизацию расположения опор станка фирмы SMS Meer по критерию наименьшего отклонения радиус-вектора и рассмотреть большее число вариантов для минимизации амплитуды колебаний поперечных смещений стержня в зоне резания на Таганрогском металлургическом заводе ОАО «ТАГМЕТ».