Исследование поведения частиц в гидродинамическом фильтре на основе численных расчетов

Процессы фильтрации и фильтрования жидкостей в настоящее время недостаточно изучены. Имеющиеся теоретические разработки по этим вопросам базируется на рассуждениях и выводах, которые зачастую не достаточно подтверждены результатами экспериментальных работ. Особенно это относится к фильтрованию высоковязких и реологически сложных жидкостей. Большинство таких жидкостей обладают неньютоновскими свойствами, эффективная вязкость которых зависит от скорости деформации. Движение таких жидкостей в пористой среде изучено мало. При построении теории фильтрации и фильтрования используются допущения и упрощения, которые не позволяют получить целостную картину процесса. Отсутствие адекватной модели гидродинамики неньютоновской жидкости в гидродинамическом фильтре является основной проблемой на пути создания общей методики расчета аналогичных аппаратов. Поэтому построение математической модели фильтрования, основанной на численном решении уравнений Навье-Стокса, весьма актуально особенно при рассмотрении многофакторных процессов, теоретическое описание которых весьма сложно.

Использование численного эксперимента при решении таких задач конкретизирует направления экспериментально-теоретического исследования процессов фильтрации и фильтрования, позволяет выявить уже на стадии проектирования оптимальные режимы работы филь-

тра, оптимизировать элементы его конструкции и сосредоточиться на основных задачах экспериментального исследования.

2.    ПОСТАНОВКА ЗАДАЧИ

В настоящее время в МГТУ им. Н. Э. Баумана на кафедре “Экология и промышленная безопасность” ведётся работа по созданию гидродинамического вибрационного фильтра, описание которого представлено в [1-4]. Процесс очистки заключается в том, что жидкость пропускают через фильтровальную перегородку, которая вращается и вибрирует вдоль оси вращения, при этом часть очищаемого потока перепускается вдоль перегородки (рис. 1).

Задача заключается в создании расчетной графоаналитической модели, с помощью которой можно было бы оценить влияние различных факторов на процесс очистки, в частности:

• -    свойств очищаемой среды (реологических свойств, плотности);

• -    параметров отделяемой твердой фаза (размера частиц и их плотности);

• -    режимов работы фильтра (частоты вращения фильтроэлемента, частоты и амплитуды его вибрации, скорости течения жидкости вдоль фильтровальной перегородки, соотношения объемов очищаемой и перепускаемой жидкости).

• 3.    СОЗДАНИЕ ГРАФОАНАЛИТИЧЕСКОЙ МОДЕЛИ

Анализ современных программных продуктов показал, что базой для расчетного исследования гидродинамических и сепарационных процессов, происходящих в фильтре, может являться программный комплекс “STAR-CD”. Использование программного продукта предполагает численное решение уравнений Навье-Стокса, осреднённых по числу Рейнольдса при заданных граничных условиях, методом конечных объёмов. На первом этапе работы создана упрощенная графоаналити-

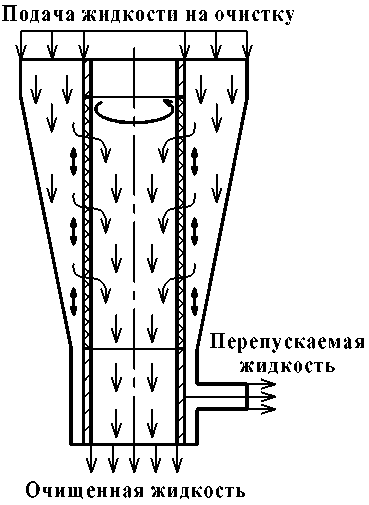
Рис. 1. Схема работы фильтра ческая модель и проведены предварительные расчеты с целью обоснования возможности использования программного комплекса для решения поставленной задачи.

Для подтверждения возможности использования результатов, полученных с использованием программного комплекса “STAR-CD”, и адекватности разработанной графоаналитической модели для изучения процессов фильтрования смоделированы и рассчитаны некоторые течения, для которых известны точные аналитические решения, и проведено их сравнение. Программа показала довольно высокую сходимость с аналитическим решением, на основании чего сделан вывод о возможности использования результатов, полученных в “STAR-CD”.

Построение геометрии

Создание модели начинается с построения её геометрии. Геометрическая модель предусматривает разбиение на 1 953 540 структурированных гексоэдрических ячеек – элементарных объёмов, в которых происходит расчет. Такое мелкое разбиение позволяет достичь сходимости решения. Ячейки сгущаются к областям образования пограничного слоя. На первом этапе работы при построении геометрии были приняты следующие упрощения:

• -    не рассматривается течение жидкости в отводящем патрубке;

• -    фильтровальный элемент, состоящий из сетки, закрепленной на каркас в виде перфорированного цилиндра, заменен эквивалентной пористой средой.

Исходные данные для расчетов

Рассматривались случаи:

• -    вращения фильтровальной перегородки с различными частотами при фильтрации ньютоновской жидкости;

• -    вращения фильтровальной перегородки при фильтрации неньютоновской жидкости с различным индексом течения.

Параметры сред, режимов и конструкции, для которых на первом этапе работы выполнялись расчеты, представлены в табл. 1.

Таблица 1. Параметры сред, режимов работы и конструкции фильтра

Наименование	Материал, значение	Примечания
Жидкая среда	Вода, 20оС Масло инд., 20оС
Твердая фаза	Железо	Плотность ρ p = 7800 кг/м3
	Карбид бора	Плотность ρ p = 2500 кг/м3
Диаметр частиц d , мкм	20; 40; 60; 100; 300; 500
Расход жидкости через фильтр, л/мин (м3/с)	2 (3,333•10-5)
Средняя скорость жидкости на входе, м/с	0,029
Частота вращения фильтровальной перегородки f , Гц	1,7; 5,0; 10,0
Фильтровальный материал	Сетка С 685	ТУ 14-1-697-2001
Расход перепускаемой жидкости	15% от полного расхода	4,999•10-6 м3/с
Расход очищенной жидкости	85% от полного расхода	2,833•10-5 м3/с
Индекс течения n	0,4; 0,6; 0,8; 1,0	Реологическая кривая жидкости описывается степенной зависимостью
Коэффициент консистенции жидкости k , Па•с(2 n - 1)/ n	0,153

Задание фильтровальной перегородки

Фильтровальная перегородка в модели задаётся эквивалентным гидравлическим сопротивлением и величиной пористости материала. Со-

противление в направлении движения потока в пористой среде описывается значение коэффициента X , примененного для канального течения. Коэффициент сопротивления X представ-

ляется в программе в виде:

X — C Re m 1 +

1 I Re

т

Pv

, 2

где С ₁, С ₂, m – константы, зависящие от типа жидкости; Re – число Рейнольдса ( Re = pv'D / p >; v' — средняя скорость жидкости в среде, м/с, Ц - динамическая вязкость жидкости, Па^с; p - плотность жидкости, кг/ м 3 ; D - характерный диаметр канала, м; т - касательное напряжение, кг/(м•с²).

Средняя скорость жидкости в среде

Qfp v = 5.P7J.             (2> где Qfp – расход жидкости через фильтровальную перегородку, м3/с; Sfp – площадь фильтровальной перегородки, м2, s - пористость фильтровального материала.

Потеря давления на единицу длины канала может быть представлена как:

пористой среды, и _— v's >, м/с; А - поверхностная площадь фильтровальной перегородки ( A — A ' / s >, м 2 .

С помощью коэффициентов a [кг/м⁴], в [кг/(м³с>] и пористости s задаётся эквивалентное гидравлическое сопротивление фильтровальной перегородки.

Канальное течение представляется как течение в ортотропной пористой среде. Поэтому значения коэффициентов a и в для направлений, где нет течения (т.е. в направлении стенок канала), берутся на 5-6 порядков выше, чем в направлении течения. Такое задание условий понимается программой как течение в одном направлении.

В нашем случае рассматривается ламинарное течение в круглом канале, поэтому коэффициент гидравлического сопротивления имеет вид [5]:

Re ^.

В уравнении (1) константы С ₁ = 64; С ₂ = 0; m = – 1.

64 Pp Re ^{- 1}

2s3 A

; в = 0.

dp    P

— = -т —

L       A' ’

где Р - периметр смоченной поверхности, м; A' – площадь поперечного сечения каналов пористой среды, м².

Из уравнения (3) следует, что:

dp A'

L P ^.

Используя уравнения (1) и (4) получаем:

C_x Re m 11 + C ²

1 I Re

dp A'

PXXA■ ⁽⁵>

После преобразования выражения (5) получаем:

В программе проведён расчет для двух жидкостей, существенно различающихся по вязкости: воды и масла. Параметры используемых жидкостей, представлены в табл. 2.

Средняя скорость прохождения жидкости через фильтровальную перегородку равняется v‘ — 7,277 • 10^-3 м/с.

Число Рейнольдса определяется по формуле:

Re — pv ' D / Ц .

Reвод = 1,085•10-1 – для воды.

Reмасл = 8,835•10-4 – для масла.

Таким образом, имеет место ламинарный режим течения.

Коэффициент a для воды:

a — 3,073 • 10 8 кг/м⁴.

Коэффициент a для масла:

a —1,555 • 10¹² кг/м⁴.

Рассчитанные значения коэффициентов a , в и пористость s подставляются в соответствующее окно программы.

dp PC 1 pu ² Re m PC 1 C ₂ ци Re m — —----------

L       2s ³ A        2s ² AD

— au + ви ,(6>

4. РЕЗУЛЬТАТЫ ПРЕДВАРИТЕЛЬНЫХ РАСЧЕТОВ

где u – приведенная скорость (определяется отношением средней скорости к доле твердой фазы

В гидродинамическом вибрационном фильтре реализуются три механизма очистки жидкости – фильтрование через пористый материал,

Таблица 2. Характеристики очищаемой среды

Параметр	Вода	Масло минеральное
Плотность, кг/м3	998,9	900,0
Вязкость динамическая, Па•с	1,01•10-3	1,53•10-1

очистка за счет действия центробежных сил и гидродинамического смыва. На данном этапе работы последний механизм не моделировался, но планируется его включение в расчет с помощью написания отдельной подпрограмм, так как непосредственно сама программа “STAR-CD” этот механизм не может учесть. Кроме того, фильтровальная перегородка, заданная как пористая среда с эквивалентным гидравлическим сопротивлением, для частиц не является преградой – все частицы проходят сквозь неё. Кроме того, фильтровальная перегородка, заданная как пористая среда с эквивалентным гидравлическим сопротивлением, для частиц не является преградой. Поэтому расчет показывает, что если частица попадает на фильтровальную перегородку, она проходит сквозь неё. Однако очевидно, если диаметр частицы больше диаметра отверстий в пористом материале, она не пройдёт через него, а задержится на его поверхности или в объеме пористой перегородки. На последующих этапах работы над программой предполагается устранение этой неточности, т.е. разработка дополнительных подпрограмм, описывающих структуру пористой перегородки, гидродинамический смыв, а также продольную вибрацию фильтровального элемента, т.е. моделирование действия всех механизмов, имеющих место при работе фильтра.

На данном этапе моделировались два случая – при неподвижной и вращающейся перегородке.

Оценка эффективности отделения частиц осуществлялась по соотношению:

N

η _f = _N ^f ⋅100% ,        (9)

где η f – показывает, сколько частиц вышло из фильтра не попав на фильтровальную перегородку в %; N f – количество частиц, не попавших на фильтровальную перегородку; N – общее количество частиц, введенных в фильтр.

Результаты предварительных расчетов фильтрования ньютоновских жидкостей

Для каждой из двух сильно отличающихся по вязкости жидкостей варьировались частоты вращения фильтровальной перегородки f , диаметр d и плотности частиц ρ p . По результатам расчета построен график зависимости величины η f от диаметра частиц и частоты вращения фильтровальной перегородки (рис. 2).

Как видно из рис. 2, существенное влияние на величину η f оказывает вязкость жидкости. Так, при частоте вращения f = 5 Гц ( 300 оборотов в минуту) в воде все частицы диаметром

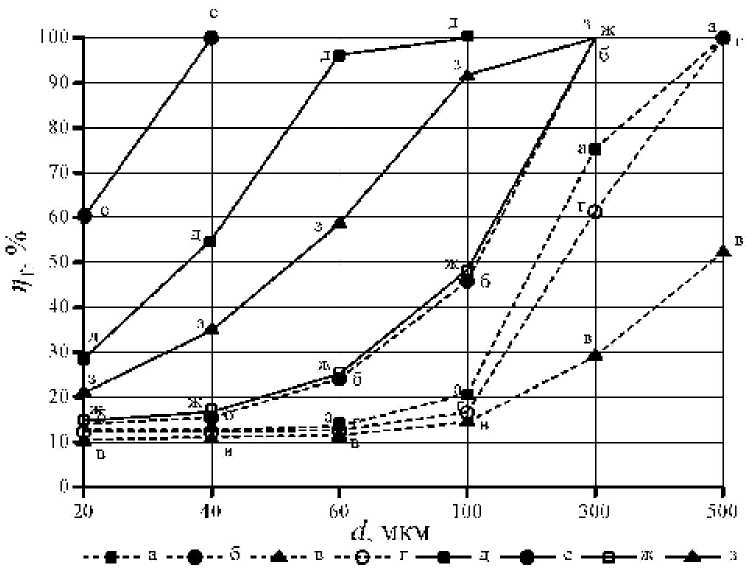
Масло: а – f = 10 Гц, ρ p = 2500 кг/м³; б – f = 10 Гц, ρ p = 7800 кг/м³; в – f = 5 Гц, ρ p = 2500 кг/ м³; г – f = 5 Гц, ρ p = 7800 кг/м³;

Вода: д – f = 5 Гц, ρ p = 2500 кг/м³; е – f = 5 Гц, ρ p = 7800 кг/м³; ж – f = 1,67 Гц, ρ p = 2500 кг/м³; з – f = 1,67 Гц, ρ p = 7800 кг/м³

Рис. 2. Зависимость величины ηf от диаметра частиц d и частоты f вращения фильтровальной перегородки больше 40 мкм и плотностью Рр = 7800 кг/м3 отделяются за счет центробежных сил и не попадают на фильтровальную перегородку (зависимость е рис. 2). В масле же при тех же режимных параметрах отделяются только 12,5 % частиц (зависимость г рис. 2). Кроме того, вид кривых на воде в исследуемом диапазоне размеров частиц имеет практически плавно возрастающий характер. Для масла же в диапазоне 20 – 60 мкм значение исследуемого параметра изменяется незначительно и составляет 10,5 –13,8 % (зависимости а, в, г рис. 2).

На рис. 2 не показаны зависимости, полученные для воды при f = 10 Гц (600 оборотов в минуту), так как в исследуемом диапазоне диаметров частиц d (от 20 до 500 мкм) значение параметра n f = 100%.

Таким образом, на основе полученных расчетных зависимостей можно прогнозировать оптимальный режим работы фильтра при известных характеристиках очищаемой жидкости, плотности и дисперсно-фракционного состава частиц загрязнения. Для маловязких жидкостей, сравнимых с вязкостью воды, нет необходимости использовать большую частоту вращения фильтровальной перегородки – даже величина f = 5 Гц дает хороший результат по очистке частиц размером до 20 мкм, а более мелкие частицы будут задерживаться фильтровальной перегородкой. Для высоковязких жидкостей, таких как масла, необходимо выбирать режимы с большей частотой вращения, не менее 10 Гц.

На рис. 4 представлен график зависимости тонкости очистки от вязкости очищаемой жидкости. Кривые построены для монодисперсных загрязнений при различных диаметрах частиц, частоте вращения фильтровальной перегородки f = 5 Гц, плотности частиц Р р = 2500 кг/м³.

Результаты предварительных расчетов фильтрования неньютоновских жидкостей

Проведен расчет гидродинамических характеристик неньютоновской жидкости для параметров, указанных в табл. 1, при частота вращения фильтровальной перегородки 5 Гц. Динамическая вязкость жидкости, соответствующая индексу течения n = 1, составляет 0,153 Па•с. Плотность жидкости 900 кг/м³. Варьировалась величина индекса течения.

В основу расчета гидравлических характеристик течения неньютоновской жидкости положена степенная зависимость Оствальда де Виля. Для степенной жидкости эффективная вязкость µ определяется следующим соотношением:

ц = kj ⁽ ” ^{- 1)/} n , (10) где µ – эффективная вязкость, Па•с; k – коэффициент консистенции, Па•с^{(2 n -1)/ n} ; j – скорость сдвига, с^-1; n – индекс течения, характеризующий

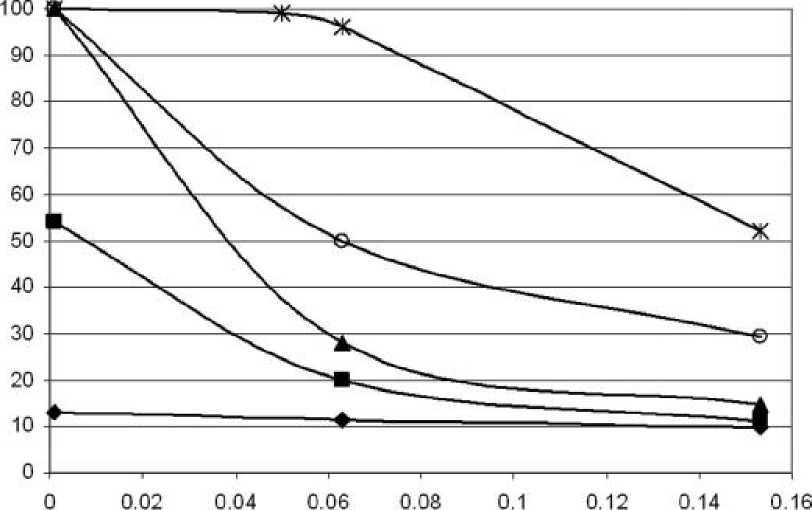
Вязкость, Па с

♦ d =10 мкм » d =40 мкм —*—d =100 мкм —в— d =300 мкм —*— d =500 мкм

Рис. 3. График зависимости величины η _f от вязкости очищаемой жидкости для разных диаметров частиц d плотностью Р р = 2500 кг/м³ при f = 5 Гц

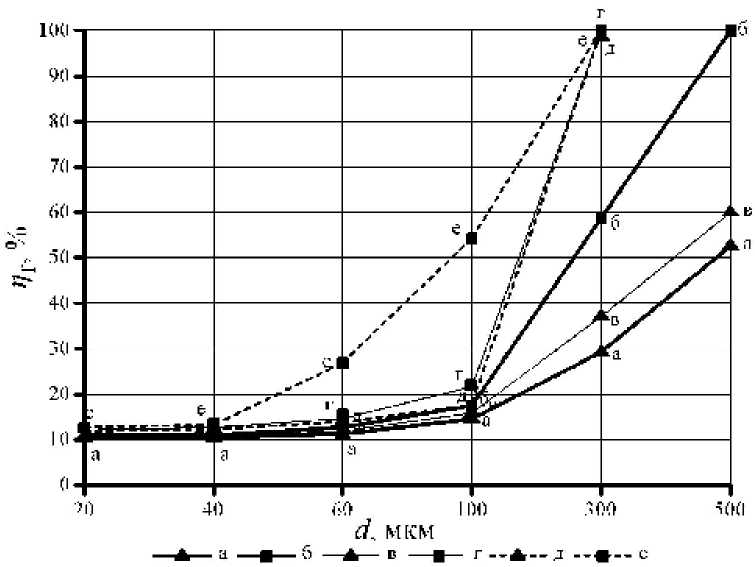
а – n = 1, ρ p = 2500 кг/м³; б – n = 1, ρ p = 7800 кг/м³; в – n = 0,8, ρ p = 2500 кг/м³;

г – n = 0,8, ρp = 7800 кг/м3; д – n = 0,4, ρp = 2500 кг/м3; е – n = 0,4, ρp = 7800 кг/м3 Рис. 4. Зависимость величины ηf от диаметра частиц d и индекса течения n при частоте вращения фильтровальной перегородки 5 Гц темп разрушения структуры и степень отклонения от ньютоновского течения.

Исследование проводилось для псевдоплас-тичной жидкости ( n < 1) [6].

По результатам расчета построен график зависимости величины η f от диаметра d и плотности частиц ρ p , и величины индекса n . Согласно рис. 4, на величину η f существенное влияние оказывает индекс течения n . При определенном размере частиц загрязнения величина η f больше при меньшем значении n . Так для частиц плотностью 7800 кг/м³ и диаметром 60 мкм при n = 0,4 сепарируются за счет вращения 27 % всех частиц, а при n = 1,0 только 11,5 % всех частиц. Такое поведение кривых объясняется тем, что величина η f зависит от вязкости жидкости, согласно рис. 3. При меньшем значении индекса течения n происходит более быстрое разрушение структуры жидкости и снижение ее вязкости, что приводит к повышению эффективности сепарации твердой фазы η f .

Это позволяет сделать вывод о том, что применение гидродинамической фильтрации позволит значительно улучшить и упростить очистку реологически сложных сред, которая связана со значительными проблемами из-за быстро снижения пропускной способности фильтровальной перегородки. Можно с очевидностью предположить, что введение вибрации фильтровальной перегородки будет являться дополнительным фактором, улучшающим отделение твердой фазы от высоковязкой неньютоновской жидкости за счет снижения ее вязкости, устранения облитера-ционных процессов в пористой структуре, разрушения осадка, образующегося на перегородке.

ВЫВОДЫ

Показана возможность математического моделирования с использование программного комплекса “STAR-CD” при разработке оптимальной с точки зрения гидродинамики и эффективности очистки конструкции гидродинамического вибрационного фильтра, что сокращает затраты на экспериментальную отработку опытного образца.

Предварительные расчеты показали, что одним из основных параметров, влияющим на процесс очистки в гидродинамическом фильтре является вязкость жидкости. Увеличение вязкости жидкости ведет к уменьшению эффективности очистки. Эффективность очистки зависит также, но в меньшей степени, от плотности частиц и частоты вращения фильтровальной перегородки.