Исследование поведения пузырей при электролизе суспензии криолитовый расплав - глинозем

содержащей вблизи катода и анода растворенные металл и газ соответственно. Последнее позволит сблизить электроды, не опасаясь интенсификации их взаимодействия. Появляется возможность «упаковать» в одну электролизную ванну множество электродов, в частности, как это практикуется при производстве магния [4]. Очевидно, суммарная площадь теплоотводящих поверхностей станет меньше, поэтому частичным решением проблемы теплоотвода служит снижение температуры электролиза за счет применения электролитов с низкой температурой ликвидуса. Применяя электролит на основе KF-AlF3, можно снизить температуру до 700 °C. Важной возможностью, которая открывается в описанных условиях, является применение инертного анода и отказ от использования углерода в конструкции ванны. Продуктом электролиза на аноде станет кислород. Предлагаемая технология решает проблему выброса вредных веществ в окружающую среду. Так, с нашей точки зрения, выглядит концепция развития процесса Эру-Холла.

Способ электролиза разбавленных суспензий изложен в работах Бека [5, 6], где частички глинозема поддерживаются во взвешенном состоянии размещенным на дне электролизера газовым генератором, Рендалла [7], согласно которым алюминий выделяют электролизом суспензии глинозема в расплавленном сульфате калия, Полякова и Симакова [2, 8, 9].

Одним из факторов, препятствующих развитию описанного способа, служит отсутствие знаний о явлениях, происходящих при электролизе высокотемпературных суспензий.

Одно из таких явлений – трехфазный поток газ – электролит – глинозем, возникающий в прианодном слое электролита. Этот поток имеет большое значение, так как от его характера зависит конвекция, величина падения напряжения в прианодном слое электролита, выход по току и в конечном итоге удельный расход электроэнергии.

Трехфазные потоки при электролизе суспензий прежде не исследовались в связи с новизной идеи об использовании суспензии в качестве среды электролиза. Однако внимание уделялось изучению двухфазных потоков газ – жидкость, а также их моделированию, в том числе и в технологии электрохимических производств [10-13].

Литературный обзор

Выделяют такие подходы к исследованию двухфазного потока газ – электролит [11]:

• 1)    на промышленном электролизере;

• 2)    на модели, отличающейся только размерами;

• 3)    на низкотемпературной ячейке, в которой протекает подобная электрохимическая реакция;

• 4)    на водной модели с подаваемым под давлением воздухом;

• 5)    на математической модели.

Предлагаемое нами высокое содержание глинозема в суспензии (более 20 об. %) в сочетании с высокой температурой затрудняет наблюдение за газогидродинамикой в прианод-ной области. Результаты, полученные при подходе 4, не так точны, как можно добиться при электролитическом выделении газа. Математическое моделирование требует владения соответствующими программными средствами и знаниями свойств неньютоновской жидкости, которыми мы не обладаем. Для исследования трехфазного потока рациональным – 856 – видится подход, при котором высокотемпературный электролиз моделируется низкотемпературным [10].

Определенный интерес представляет исследование Алама и соавт. [10], в котором на низкотемпературной модели алюминиевого электролизера с горизонтальным расположением электродов изучалось поведение пузырей кислорода, образуемых на поверхности анода в результате электрохимической реакции

CuSO4 (водн) + H2 O ^ Си (тв) + H2SO4 (водн) +1/2 O2 (г).        (1)

Процесс (1) с выделением газа, согласно [10], подобен таковому в электролизере Эру-Холла:

2Al2O3 + 3С(тв) ^ 4Al(ж) + 3CO2(г).                           (2)

Для обеспечения геометрического подобия были соблюдены все пропорции электролизера Эру-Холла в масштабе 1:4. Динамическое подобие было обеспечено путем сравнения критериев подобия. По мнению авторов, критериями, характеризующими движение газа и жидкости, а также размер и форму пузырей, являются:

• •    Модифицированный критерий Фруда, равный отношению силы инерции к архимедовой силе. Критерий Фруда применяется при моделировании движения жидкости и газа в случаях, когда влияние внешних сил существенно. В общем случае критерий Фруда имеет вид [14]

Fr = υ ^х , gL

где υ х – характерный масштаб скорости; g – ускорение силы тяжести; L – характерный размер области, в которой рассматривается течение. Модифицированный критерий Фруда, представлен в [10] зависимостью

(pg• q2) Fr * =

(pi - pg) gL, где ρl – плотность жидкости; ρg – плотность газа; q – удельная скорость газовыделения; L – длина анода. Преобразование критерия Фруда (3) в модифицированный критерий (4) позволяет учесть электрохимический характер образования газа.

• •    Критерий Этвеша, равный отношению внешних сил (архимедовой силы) к поверхностному натяжению. Он рассчитывался в [10] как

(g (Pl- Pg) • L2) σ,

где σ – поверхностное натяжение жидкости. Критерий Этвеша также известен в литературе как критерий Бонда и применяется для характеристики формы пузырей или капель жидкости, движущихся в объёме другой жидкости.

• •    Критерий Мортона характеризует наряду с критерием Этвеша форму пузырей и капель, движущихся в жидкости. В [10] значение критерия было найдено как

( g η _l ⁴ ( ρ _l - ρ _g )) ( ρ ² l σ ³ )

где η – кинематическая вязкость электролита. Критерий Мортона можно также записать как l комбинацию критериев Вебера, Фруда и Рейнольдса:

We ³

Mo =         .

Fr ² ⋅ Re ⁴

Очевидно, характер движения пузырьков и жидкости изменится при смене горизонтальной ориентации электродов на вертикальную. Укше и соавт. [13], а ранее Бухбиндер [12] исследовали гидродинамику электролитического производства магния и свинца на модели с вертикальными электродами. Согласно авторам, скорость движения пузырей в двухфазном потоке описывается в общем виде уравнением

υ = f ( h , l , η l , q , g , ρ l , σ ) ,                                                         (8)

где υ – скорость движения пузырьков, м/с; h – высота электрода, м; l – межполюсное расстояние, м.

Для обеспечения подобия модели и натуры в [13] было выведено критериальное уравнение пи ли phи

υh=B(qh)m⋅(gh2)n⋅( σ )q ⋅(h)p,(9)

η η η2    ρh2

υh где критерий Рейнольдса был функцией четырех других критериев: Бухбиндера, Галилея, ηl

Вебера и геометрического симплекса.

σ

В (9) критерий 2 , как легко видеть, оказался размерным. Это обстоятельство сделало ρlh необходимым уточнение уравнения (9).

Параметры моделирования

Уравнение (8) адекватно описывает картину движения пузырей в жидкости, близкой к ньютоновской. Но для случая движения в суспензии видится необходимым введение по крайней мере двух параметров:

π _n = V _s V _m ,                                                          (10)

характер изучающего стесненность потока твердой фазой (глиноземом) и равного отношению объема твердой фазы V s к общему объему смеси V m , и

π sed ⁼ ρ l ρ s ,                                                            (11)

характеризующего скорость седиментации глинозема в электролите, где ρ_s – плотность твердой фазы смеси. Таким образом, уравнение (8) для случая суспензии приобретает вид

и = f (h, l щ, q, g, Pl ,a,n ,nsed).

Применяя π-теорему [15, 16] и метод анализа размерности [17, 18], можно представить уравнение (12) в виде зависимости между безразмерными критериями подобия и симплексами. Для определения критериев зададим три параметра: кинематическую вязкость, плотность и высоту электрода. Из восьми размерных параметров получим пять безразмерных комплексов и симплексов, а также два безразмерных симплекса: π_n , отражающий неньютоновский характер течения, и π , отражающий стесненность потока твердой фазой.

sed

Из уравнения (12) получились следующие критерии подобия:

n (Re) = Uh(13)

П qh n .^=(14)

^з( Ga) = ghT,(15)

ηl oh n4(We* = -.-,(16)

η l ρ

h

" 5 =

π = Vs .(18)

n V_m

πsed=ρlρs,(19)

Из найденных критериев π 1 является критерием Рейнольдса, π 2 – критерием Бухбиндера [13] (также известным как модифицированный критерий Рейнольдса), π₃ – критерием Галилея, π 4 – критерием Вебера. Полученные критерии подобия согласуются с результатами [13]. Уточнен критерий Вебера, представленный в отличие от полученного в [13] в виде

π 4 ( We *) = ₂ . (20) ηρ

В качестве электролита модели использовали 20%-ный водный раствор H2SO4. Способ производства алюминия электролизом высокотемпературной суспензии в нашем случае подразумевает применение расплавов KF-AlF3 [19]. Результат анализа подобия газовыделения в ячейке для производства алюминия (натура) и в низкотемпературной модели представлен в табл. 1.

Три из шести критериев подобия, включая критерий Бухбиндера, учитывающий удельную скорость газовыделения, численно равны. Равенство геометрических симплексов говорит о соблюдении полного геометрического подобия систем. Значения критериев Галилея и критериев Вебера достаточно близки. Рассматриваемые явления отвечают требованиям третьей теоремы подобия [15], и можно говорить о приблизительном подобии двух явлений.

Таблица 1. Свойства модели и натуры

Параметр	Натура	Модель
Электролит	50 мол. %KF-50 %AlF 3	20 % H 2 SO 4
Температура, °С	700	50
Плотность электролита, кг/м3	2114 [20]	1120
Кинематическая вязкость электролита, м2/с	1,28*10-6	7,41*10-7
Динамическая вязкость электролита, Па*с	0,00271 [21]	0,00083
Поверхностное натяжение электролита, Н/м	0,138 [22]	0,0746
Удельная скорость газовыделения, м3/м2с	0,0001	0,0001
Анодная плотность тока, кА/м2	0,73	1,9
Высота электрода, м	0,15	0,1
Межполюсное расстояние, м	0,02	0,014
Критерии подобия
Критерий Бухбиндера	16,24	16,24
Критерий Галилея	2*1010	1,78*1010
Критерий Вебера	5,96*106	0,12*106
Геометрический симплекс	7	7
Неньютоновский симплекс	0,3	0,3
Седиментационный симплекс	0,47	0,83

Методика экспериментов

Были сконструированы ячейки двух типов: ячейка 1 для наблюдения за движением пузырей спереди (рис. 1) и ячейка 2 для наблюдения за движением пузырей сбоку (рис. 2).

Информация, полученная на ячейке 1, по нашему мнению, может быть лишь частично экстраполирована на натуру в связи с различиями в токораспределении и отсутствием полного геометрического подобия. В ячейке 1 в отличие от натуры часть анодного тока выделяет газ на боковых стенках электрода, так как катод расположен с изолированной стороны анода. Тем не менее процессы роста, коалесценции, подъема одиночных пузырей к границе электролит – воздух, образования граничного слоя не должны иметь существенных отличий от таковых при электролизе суспензии криолитовый расплав – глинозем.

Ячейка 2 является моделью для электролизера нового типа. Все данные, полученные на ней, с нашей точки зрения, могут быть экстраполированы на натуру.

Электроды из нержавеющей стали подключали к потенциостату AUTOLAB PGSTAT302, измерения проводили в гальваностатическом режиме. Электроды располагались вертикально на расстоянии 1,5 см друг от друга. Уровень электролита составил 5 см в ячейке 1 и 10 см – в ячейке 2. Плотность тока изменялась в диапазоне от 0,05 до 0,25 А/см2.

Камеру Nikon D3100 установили перед стеклянной стенкой ячейки. Частота кадров видеосъемки составила 30 с-1.

Видеосъемка осуществлялась для выяснения параметров движения пузырей, их коалесценции, толщины и геометрии пузырькового слоя и слоя на границе электролит – воздух. Видеозаписи анализировали с помощью программы Tracker.

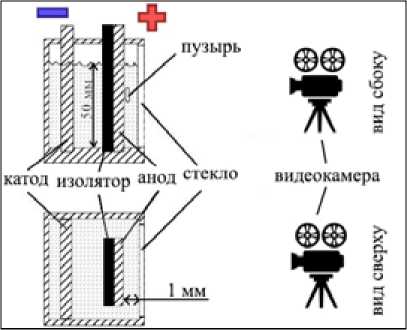
Рис. 1. Схема ячейки 1 для наблюдения за движением пузырей спереди

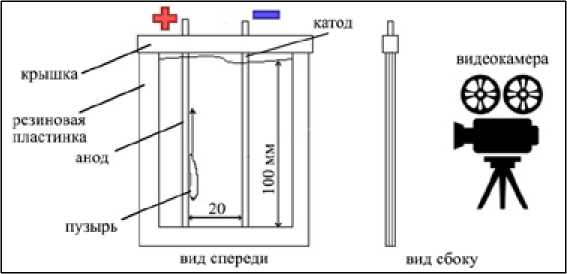
Рис. 2. Схема ячейки 2 для наблюдения за движением пузырей сбоку

Объем пузырей определялся на ячейке 1 с допущениями, что их толщина равна 1 мм (соответствует расстоянию между электродом и стеклом) и электрод не имеет неровностей. Площадь пузырей рассчитывали с помощью анализа изображений в программе CorelDraw.

Результаты экспериментов и их обсуждение

При совершении электрической работы в нашем случае на аноде выделяется кислород, а на катоде – водород. Пузыри кислорода, образуясь в микротрещинах и на шероховатостях поверхности электрода, увеличиваются сначала посредством абсорбции растворенного газа, а затем за счет коалесценции. После достижения критического объема пузыри отрываются от электрода и поднимаются к поверхности, продолжая увеличиваться в размерах. Дойдя до поверхности, пузырь замедляет движение, после чего пробивает пленку на межфазной границе.

Движение пузырей в суспензии создает трехфазный поток и разделяет изначально равномерную суспензию на несколько слоев. Укрупненно можно выделить пять слоев в межэлектродном пространстве:

• •    пузырьковый слой, протекающий вдоль электрода, выделяющего газ, образующийся из пересыщенного раствора вплотную к электроду или на некотором расстоянии от него;

• •    подвижный слой суспензии, движущийся вверх вместе с пузырьковым слоем;

• •    слой суспензии, обтекающий пузыри и движущийся вниз;

• •    горизонтальный слой суспензии с пузырями (ГССП) на границе электролит – воздух;

• •    неподвижный слой суспензии, находящийся на таком расстоянии от электрода, на котором влияние движения пузырькового слоя не ощущается.

Первые четыре из вышеописанных слоев назовем трехфазным слоем (ТФС).

Стадии жизни пузыря

Поведение пузырей в суспензии можно сравнить с их поведением в ньютоновской жидкости. Жизненный цикл пузыря в суспензии делится на стадии таким же образом, как это делалось для пузыря в жидком электролите без взвесей [23]: образование, рост, отрыв, подъем, задержка пузыря на границе электролит – воздух, разрыв.

Принципиальная разница между процессами эвакуации газа из суспензии и из жидкого электролита заключается в скорости протекания стадий жизненного цикла пузырей. Низкая скорость эвакуации газа из суспензии может стать причиной большого содержания газа в при-анодном слое, что негативно скажется на технологических параметрах электролиза. В частности, ухудшится выход по току, увеличится электрическое сопротивление в межэлектродном слое, произойдет интенсификация конвективного переноса электролита с растворенными продуктами электролиза (кислородом и алюминием), что в итоге приведет к увеличению удельного расхода электроэнергии.

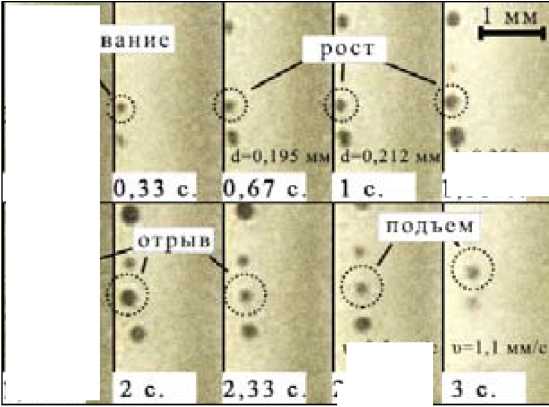
Стадии «жизни» пузыря изображены на рис. 3.

Стадия образования пузыря не будет подробно рассмотрена в статье, поскольку высокое содержание твердой фазы в суспензии, низкая скорость видеосъемки и макроскопический масштаб исследования создают трудности для определения характера и закономерностей этого процесса.

Рост пузыря наблюдается на протяжении всего жизненного цикла. Наиболее заметное увеличение объема пузыря достигается за счет поглощения им других пузырей (коалесценции).

U 'fl.S UUl

2Т66 с.

Рис. 3. Стадии жизни пузыря в суспензии (ячейка 2, 0,25 А/см2)

4^0,353 MN

1,33 с.

На стадии отрыва пузырь удаляется от поверхности электрода на ~ 0,2 мм, после чего начинается стадия подъема. Благодаря обтеканию пузыря электролитом по мере его подъема, слой суспензии, внутри которого происходит подъем, обогащается жидкой фазой. Траектория движения пузыря на стадии подъема не строго вертикальна и зависит от локальных изменений гидродинамического сопротивления в суспензии. В связи с низкой скоростью подъема (по сравнению с движением в традиционных электролитах) за время приближения к границе электролит – воздух некоторые пузыри достигают 20 мм в длину. Замедлено истечение жидкости из пленки между пузырем и окружающей атмосферой. Пузыри могут аккумулироваться в этом слое, образуя пену.

Форма пузырей на начальных стадиях жизни близка к сферической, как это видно на рис. 3, но по мере роста и подъема пузыри приобретают форму овала. Приближаясь к границе электролит – воздух, пузыри, сталкиваясь с барьером в ГССП, снова могут приобрести сферическую форму.

Траектории движения пузырей

Практический интерес представляют особенности подъема и эвакуации пузырей, в частности траектории движения вдоль электрода, механизм эвакуации крупных пузырей, их взаимодействие между собой. Для визуализации этих процессов нами был проведен ряд опытов на ячейке 1, которая давала возможность наблюдения за рабочей поверхностью электрода.

На рис. 4 изображена картина подъема пузырей. Изображения получены при плотности тока 0,05 А/см2.

Траектории пузырей, образующихся в разных областях межэлектродного пространства, при приближении к ГССП могут сливаться в одну, образуется «газовый канал», как это видно на рис. 4. Например, в интервале времени с 0 до 0,67 с по этой траектории поднимается пузырь, образованный в левой части электрода, а с 0,83 до 1,5 с – образованный в правой части. Наличие сложных траекторий свидетельствует о неравномерности гидродинамического сопротивления суспензии.

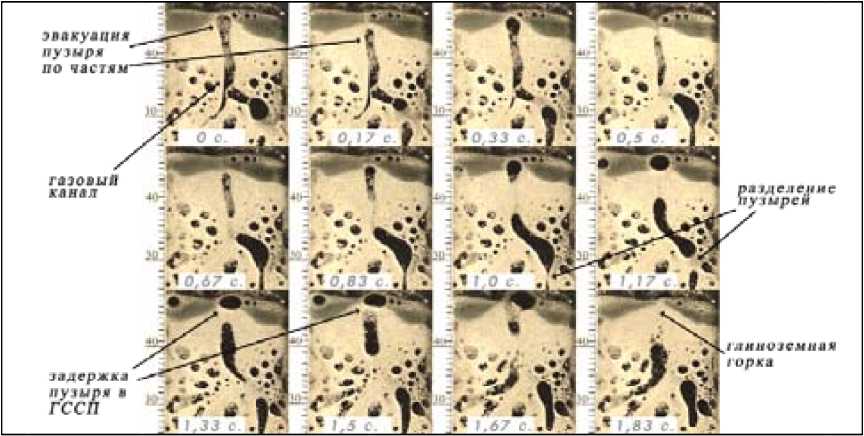
Рис. 4. Подъем и эвакуация пузырей (ячейка 1, 0,05 А/см2)

Пузыри длиной более 10 мм часто не способны пройти через границу электролит – воздух полностью. В интервале с 0 до 1 с наблюдается эвакуация пузыря по частям.

Вариантом взаимодействия пузырей между собой может быть не только коалесценция, но и отделение одного пузыря от другого, как это видно с 1 по 1,17 с на примере крупного пузыря, находящегося в центре изображения.

Задержка пузырей в ГССП видна с 1 до 1,67 с. Пузырь пересекает границу только после того, как коалесцирует с другим, более крупным пузырем. В местах пересечения границы пузырями образуется глиноземная горка.

Скорость подъема пузырей

Требуют решения вопросы о том, насколько влияет удельная скорость газовыделения на скорость подъема пузырей и как скорость подъема изменяется в зависимости от высоты. Эти параметры будут иметь значение при выборе размеров электрода и плотности тока при электролизе суспензии криолитовый расплав – глинозем.

На рис. 5 изображена зависимость скорости подъема пузырей диаметром 4-6 мм от глубины при разных плотностях тока.

Наибольшей скорости (25 мм/с) пузыри достигают на глубине от 15 до 20 мм от уровня электролита при плотности тока 0,2 А/см2. Скорости подъема пузырей диаметром 1-2 мм в различных расплавах (ньютоновских жидкостях) составляли от 20 до 35 см/с [24].

После достижения максимальной скорости пузырь приближается к границе с воздухом и его скорость снижается. Влияние удельной скорости газовыделения на скорость подъема пузырей больше ощущается в нижней части трехфазного потока. Усредненная по плотности тока скорость подъема пузырей представлена на рис. 6.

На рис. 6 видно снижение скорости подъема при пересечении ГССП. Наибольший градиент скорости 6u z /5 h _r наблюдается на начальной стадии подъема пузыря, на глубине 40-50 мм. На глубине 30–35 мм скорость подъема пузырей снижается, что может быть вызвано взаимодействием с другими пузырями и локальными изменениями гидродинамического сопротивления в суспензии.

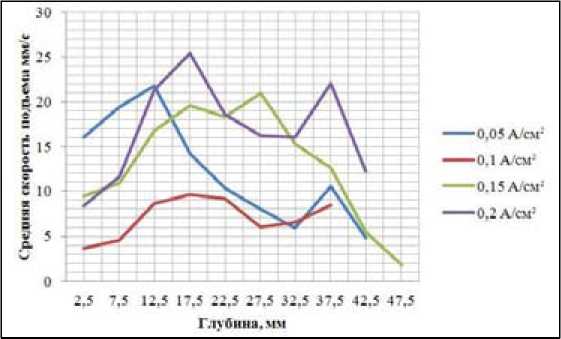
Рис. 5. Зависимость средней скорости подъема пузырей υ z от глубины и плотности тока

Кривая зависимости скорости подъема от глубины описывается уравнением uz =-0,4443h2 + 4,063 3h + 6,3 562                                             (21)

с величиной достоверности аппроксимации 0,8382.

В результате наблюдений не было установлено явных ограничений в размерах электрода для электролизера нового типа. По нашему мнению, технологичная высота электрода может составлять от 10 до 50 см.

Рост пузырей и коалесценция

Определенный интерес представляют параметры роста пузырей, в частности, скорость роста пузырей и характер их коалесценции. На рис. 7 даны фотографии пузырей диаметром менее 1 мм, коалесцирующие между собой.

Коалесценция обеспечивает рост пузырей, ускоряет их подъем. На рис. 7 жирными линиями выделены коалесцирующие пузыри. За интервал времени меньше четверти секунды наблюдается три акта коалесценции пузырей на площади в несколько мм2. Продолжительность самого акта коалесценции мала, во всяком случае, она меньше 0,03 с. Коалесцировать

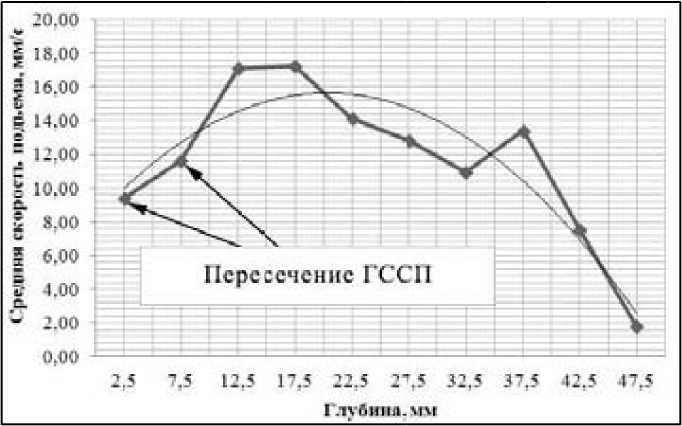
Рис. 6. Средняя скорость подъема пузырей как функция глубины h _г

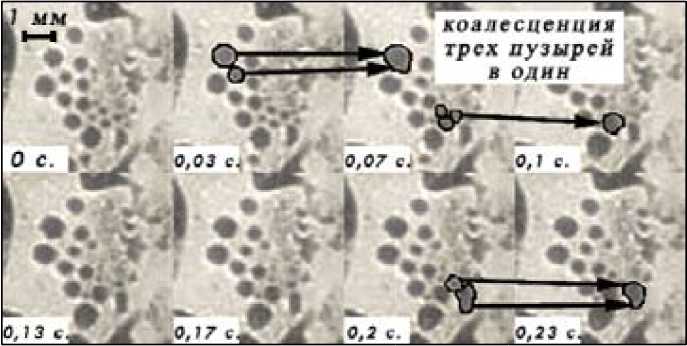
Рис. 7. Коалесценция пузырей (ячейка 1, 0,2 А/см2)

могут два пузыря и более. За 0,07–0,1 с может наблюдаться коалесценция трех пузырей в один.

Как известно, скорость подъема, помимо вязкости жидкости и разности плотностей пузыря и среды, зависит от объема пузыря и архимедовой силы [25]. Объем пузыря и скорость его изменения – важный параметр с точки зрения технологии, который следует принимать во внимание. Вокруг пузырей, которые в суспензии имеют сложную форму, при их всплывании создаются потоки, которые перемещают жидкость от лобовой поверхности к тыльной. Зависимость объема пузыря от времени изображена на рис. 8.

Наблюдается равномерное увеличение объема пузыря в первые полторы секунды, после чего объем начинает меняться скачкообразно вследствие коалесценции с крупными пузырями и разделения. Всего за две с половиной секунды объем пузыря увеличился с 0,3 до 6,92 мм3. После этого исследуемый пузырь был поглощен более крупным пузырем.

Кривая зависимости объема этого пузыря V_п от времени τ описывается уравнением

^V = 0,³⁵⁸⁸e"'"” ’                                                           ⁽²²⁾

с величиной достоверности аппроксимации 0,9423.

На рис. 9 представлена зависимость скорости роста пузыря от времени.

Максимальная скорость роста объема для представленного пузыря составила более 15 мм3/с в момент поглощения другого крупного пузыря. Средняя скорость роста была 2,68 мм3/с. Следует отметить, что она может значительно различаться для разых пузырей, а некоторые пузыри могут сохранять объем до десяти секунд и более. Такие пузыри обнаруживаются, в частности, в ГССП.

ГССП

Слой суспензии на границе с воздухом имеет большое значение в контексте реализации эффективной технологии производства алюминия. В этом слое наблюдается скопление пузырей малых размеров (0,01-1 мм), которые не удаляются самопроизвольно и слабо коалесцируют. Образование такой пены может стать причиной нежелательного взаимодействия продуктов электролиза и снижения выхода по току.

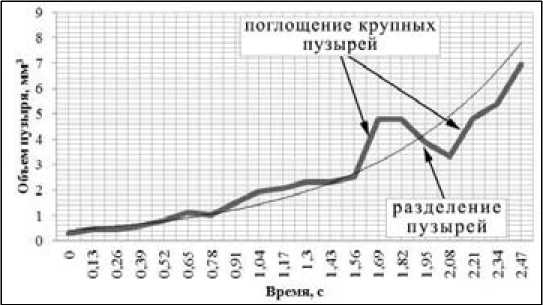
Рис. 8. Зависимость объема пузыря от времени (ячейка 1, 0,05 А/см2)

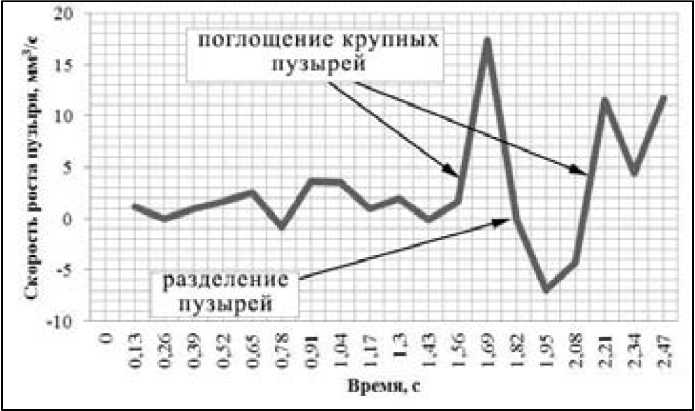
Рис. 9. Зависимость скорости роста пузыря от времени (ячейка 1, 0,05 А/см2)

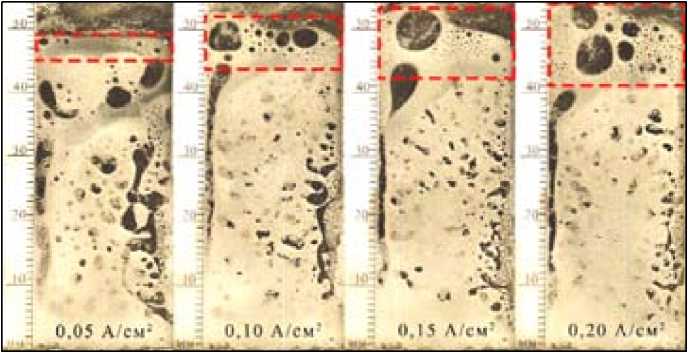
Рис. 10. Слой ГССП (ячейка 1)

Толщина ГССП зависит от удельной скорости газовыделения. На рис. 10 изображен ГССП при разных плотностях тока. Изображения сняты через 15 с после начала электролиза. На рисунке видно, что количество пузырей, аккумулированных в ГССП, тем больше, чем больше плотность тока. С увеличением плотности тока увеличивается и толщина ГССП. Если при плотности тока 0,05 А/см2 она составляет около 4 мм, то при 20 А/см2 увеличивается до 13 мм. Газосодержание в ГССП равно около 60 %. В связи с его большим омическим сопротивлением ток распределяется неравномерно.

Толщина трехфазного слоя

Практический интерес представляет вопрос о том, на каком расстоянии от электрода, выделяющего газ, будет ощущаться влияние трехфазового потока. От ответа на этот вопрос зависит межполюсное расстояние, которое может быть установлено без высокой скорости обратной реакции. Трехфазный слой содержит пузыри сферической и овальной форм длиной до 20 мм, движущиеся в слое суспензии, обогащенном жидкой фазой по сравнению с исходной суспензией. В то время как крупные пузыри поднимаются вверх, электролит вместе с частицами глинозема и маленькими пузырями обтекает их, двигаясь в противоположном направлении. При – 867 – подъеме нескольких крупных пузырей, двигающихся один за другим, суспензия, находящаяся между ними, и маленькие пузыри в этой суспензии двигаются в том же направлении. Достигая поверхности, крупные пузыри удаляются, а маленькие часто остаются на поверхности, образуя слой пены.

Толщина трехфазного слоя увеличивается по мере приближения к границе электролит – воздух, но не превышает 2,2 мм (рис. 11).

Удельная скорость газовыделения (плотность тока) имеет определенное влияние на толщину ТФС.

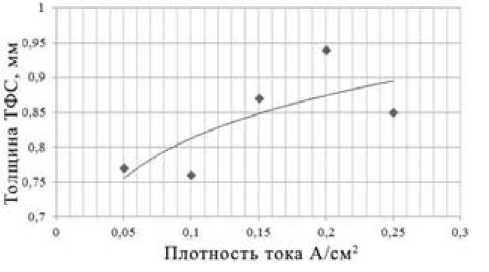
На рис. 12 представлена зависимость усредненной по высоте толщины ТФС от плотности тока.

Толщина ТФС δ _т.с. слабо зависит от удельной скорости газовыделения (плотности тока i ). Наибольшее значение (0,94 мм) соответствует плотности тока 0,2 А/см².

Кривая зависимости толщины ТФС от плотности тока описывается уравнением

^ т . с . = ⁰7⁵⁵ⁱ °’¹⁰⁵⁶                                                                       (23)

с величиной достоверности аппроксимации 0,5732.

Толщина ТФС увеличивается по мере приближения к границе электролит – воздух (рис. 13).

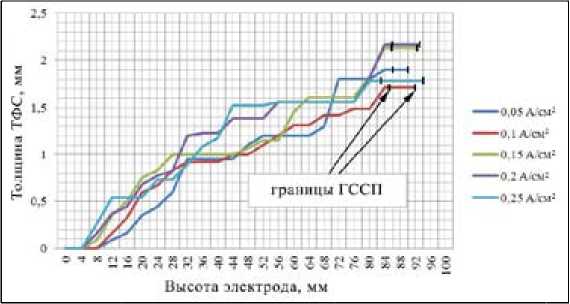
Рис. 11. Зависимость толщины ТФС от высоты при разных плотностях тока (ячейка 2)

0,05       0,1       0,15       0,2       0,25

Плотность тока А/см:

Рис. 12. Зависимость толщины ТФС от плотности тока (ячейка 2)

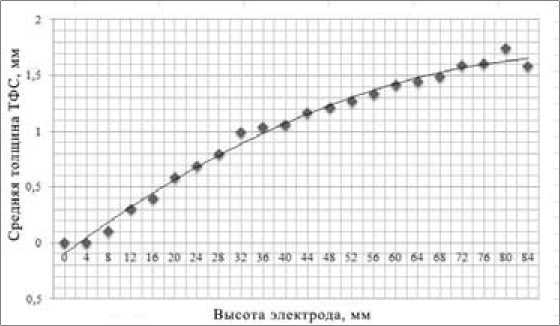
Рис. 13. Изменение толщины ТФС при приближении к ГССП (ячейка 2)

ТФС обнаруживается на высоте 4-8 мм. Градиент толщины пузырькового слоя 85 т с /8h снижается по мере приближения к ГССП.

Толщина ТФС как функция высоты h описывается уравнением

5 т с . = - 0,0031 h ² + 0,1537 h + 0,2472                                     (24)

с величиной достоверности аппроксимации 0,9908.

Выводы

• 1.    Качественно-количественная информация, полученная на модели электролизера нового типа, позволяет говорить об отсутствии непреодолимых препятствий для эвакуации газа из межэлектродного пространства при электролизе суспензии расплав – глинозем. Толщина пузырькового слоя не превышала 2,2 мм, что делает возможным установить межэлектродное расстояние даже менее 1 см и кардинально улучшить ключевые параметры электролиза: удельный расход электроэнергии, удельную производительность и себестоимость алюминия.

• 2.    Возможности управления конфигурацией трехфазного слоя и токораспределением могут открываться за счет изменения ориентации электродов относительно друг друга.

• 3.    Требует решения задача уменьшения ГССП. «Упростить» пересечение границы пузырями может система принудительной эвакуации газа. Предполагается исследовать возможность эвакуации газа через каналы внутри электрода, что может положительно сказаться на омическом сопротивлении, уменьшив количество пузырей в ТФС и ГССП.

Дальнейшие исследования будут направлены также на установление влияния содержания твердой фазы в суспензии, ее гранулометрического состава, наклона электродов на газогидро-динамику ТФС при электролизе суспензии криолитовый расплав – глинозем.

Работа выполнена при финансовой поддержке Сибирского федерального университета.