Исследование повышающего преобразователя напряжения с переключением при нулевых значениях тока

Необходимость увеличения мощности оборудования, которое входит в космические спутниковые системы, ставит задачу увеличения удельных энергетических характеристик систем электроснабжения космических аппаратов (СЭС КА). В качестве вторичных источников электропитания СЭС КА используются импульсные преобразователи напряжения (ПН). Для увеличения удельной мощности ПН необходимо увеличивать частоту преобразования, что в классических схемах ПН приводит к увеличению мощности потерь на переключение ключевых элементов (КЭ). К настоящему времени опубликовано много работ, где рассматриваются различные типы ПН с резонансным контуром (РК) в цепи силовых ключей, которые можно разделить на два больших класса: ПН, использую- щие режим переключения КЭ при нулевых значениях тока (ПНТ-преобразователи), и ПН, использующие режим переключения КЭ при нулевых значениях напряжения (ПНН-преобразователи) [1; 2]. Это два основных режима работы КЭ с использованием явления резонанса.

Можно выделить следующие типы высокочастотных ПН с использованием РК: резонансные, квазире-зонансные, с резонансным переключением. Квазире-зонансные ПН (преобразователи с дозированной передачей энергии), как и традиционные преобразователи с широтно-импульсной модуляцией, характеризуются однонаправленной передачей энергии в нагрузку. Методика переключения при нулевом напряжении и при нулевом токе применима ко всем основным способам импульсного преобразования электрической энергии: понижающим, повышающим и инвертирующим преобразователям, а также прямоходовым, обратноходовым, полумостовым и мостовым инверторам [3].

Таким образом, возможным решением обозначенной проблемы является применение методики переключения при нулевом токе, особенностью которой является снижение потерь мощности при переключении и, как следствие, увеличение КПД, а также возможность увеличения частоты преобразования, что в свою очередь увеличивает удельные энергетические характеристики. Так как через ключи протекает ток резонансного контура, имеющий синусоидальный характер, то улучшается электромагнитная совместимость (ЭМС) источника питания с приемопередающим оборудованием. Однако резонансный контур оказывает влияние на динамические характеристики источника. Целью данной работы было исследование этого влияния.

Примером ПНТ-преобразователя может служить повышающий преобразователь напряжения с широтно-импульсной модуляцией (ШИМ) и переключением при нулевом токе, предложенный в [4]. Упрощенная электрическая схема такого ПН представлена на рис. 1, а диаграммы работы – на рис. 2.

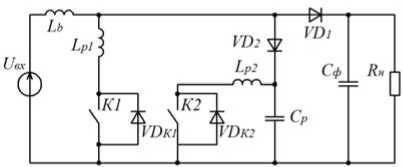
Рис. 1. Схема повышающего ПНТ-преобразователя напряжения с ШИМ

Один цикл работы данного преобразователя можно разбить на девять этапов.

Этап 1 ( T ₀– T ₁). До момента Т ₀ входной ток I _вх протекает через выпрямительный диод VD1. В момент времени Т 0 включается главный ключ К 1 и выходное напряжение прикладывается к резонансной индуктивности L р 1. Ток через К 1 и L р1 линейно увеличивается до момента, когда он достигает значения I вх . Это момент времени Т 1 .

Этап 2 ( T 1 – T 2 ). Входной ток протекает через К 1 и L р 1. В этом режиме выходной диод остается запертым и напряжение на конденсаторе фиксирует выходное напряжение.

Этап 3 (T2–T3). В момент времени Т2 включается вспомогательный ключ К2 и Ср разряжается через него. Когда напряжение на конденсаторе достигает нуля, в момент времени Т3 включается диод VD2 и режим заканчивается.

Этап 4 (T3–T4). В момент времени T3 диод VD2 начинает проводить, а конденсатор Ср заряжается отрицательным напряжением. Токи, протекающие через ключи, уменьшаются, и этот режим закончится, когда ток через главный ключ достигнет нуля. Так как диод VD2 проводит ток, то напряжение на диоде VD1 увеличивается, а напряжение на конденсаторе уменьшается.

Этап 5 ( T ₄– T ₅). В момент времени T ₄ ток через К 1 достигает нуля и встречно-параллельный диод VD_{К 1}

начинает проводить.

Этап 6 ( T 5 – T 7 ). В момент времени T 5 ток через К 2 достигает нуля и встречно-параллельный диод VD К 2 начинает проводить. В момент времени T 6 , когда ток через К 1 и К 2 достигает отрицательного пика, сигналы управления затворами К 1 и К 2 становятся запирающими и оба ключа выключаются при нулевом токе.

Этап 7 ( T 7 – T 8 ). Конденсатор C р заряжается в процессе резонанса с L _р1. Этот режим закончится, когда ток через встречно-параллельный диод VD_{К 1} достиг-

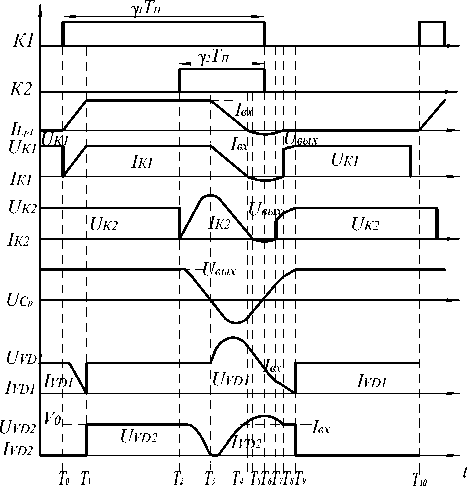
Рис. 2. Временные диаграммы режимов работы силовой части

нет нуля.

Этап 8 ( T 8 – T 9 ). Входной ток протекает через VD 2, заряжая C р. Напряжение на конденсаторе линейно возрастает, пока в момент времени T 9 не достигнет U вых .

Этап 9 ( T 9 – T 10 ). Когда U C р достигнет U вых , VD 2 закроется и VD 1 начнет проводить. Так как напряжение C р фиксируется на U вых , то VD 2 выключается при нулевом напряжении. В течение режима I вх протекает на выход через VD 1.

Далее для анализа динамических характеристик системы необходима динамическая модель системы.

Воспользовавшись методикой, описанной в [5], получим передаточную функцию ПН. Для этого составим уравнения для элементов вектора состояния ( U c ф = U вых , I L b = I вх ):

•

U вых

-^ вых + I Lb- - I L¹- t G [0, T ),

C ф R н    C ф    C ф       ¹

, 'ы 1 G [ T , T 9 ),

C _ф R _н

-U L,

—вых + -L^t G [T9, Tn ).

C _ф R _н C _ф

I Lb = ^

(U вх   U вых ) t g [0, T ),

L b

^U вх L_b ( U вх

t G T , T 3 ),

Lb

U )

— t G [ 7 3 , T 9 ),

(Uвх__Uвых ) , ГТ T \ t G [ T9, Tn ).

Lb

У =

Из полученных уравнений составим системы уравнений для каждого временного интервала:

-

1       1 "

0 -1 _ L b

- 1

0 J J 0

UBX вх I Lp1 U CP _

• U вых • _ I Lb _

=

C » R н C 2*     0 _ Lb         _

U вых _ I Lb _

+

C ф 0

’

- (2)

U вых =

[ 1

0 ]

U вых _ I Lb _

,

• и		f^^ °!	Vu 1		■ 0
вых	=	C ф R н	вых	+	1
I Lb _		_ 0     0 _	_ I Lb _		_ L b

U вых

0 0 !	UBX вх
0 0	I Lp 1	,
J	U CP _		- (3)

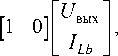
• и		'X2- "1	Vu 1		■ 0
вых	=	C ф R н	вых	+	1
_ I Lb _		_ 0     0 _	_ I Lb _		_ L b

-1

L b _

U вх

I Lр 1

.Ucp J r (4)

U_BH x= [ 1 0 ] вых

-1

U вых

_ I Lb

C ф R н

C ф

U вых

U вх

-

Lb

I Lb

+

Lb

I Lр 1

,

. UCP J

UBHx=[1 0]

вых

Далее будем использовать обозначение матриц пространства состояния.

Для учета времени работы на каждом этапе используем весовые коэффициенты:

T- = k, ,

¹ T _П

T 3

-

T 1

T П

= ^y' ^{- k} 2 ^{- k}1 ,

T 9

-

T П

T

— = k ₃ + k ₂,

T — T

T^ = 1 -Y-k 3 .

T _П

Уравнения пространства состояний для всего периода преобразования имеют вид

A 1 ^k1 ⁺ A 2 ( y' ^{- k} 2 ^{- k} 1 ) ⁺ A 3 ( k 3 ⁺ k 2 ) ^{+ +} A 4 ( 1 ^-y'^- k 3 )

" B 1 k 1 + B ₂ ( y' k ₂ - k 1 ) + B ₃ ( k ₃ + k ₂ ) +’

_+ ^B 4 ( 1 ^{-y- k} 3 )

C1 k1 + C2 (y - k2 - k1) + C3 (k3 + k2) + +C4 (1 -y'-k3)

1 x +

D 1 ^k1 ⁺ D 2 ( У'^{- k} 2 ^{- k} 1 ) ⁺ D 3 ( ^k 3 ^{+ k} 2 ) ^{+ +} D 4 ( 1 ^-y'^- k 3 )

u .

Заменим каждую переменную суммой постоянной части и малых возмущений, составляющими второго порядка пренебрегаем:

A 1 k 1 + A ₂ ( y - k ₂ - k 1 ) + A ₃ ( k ₃ + k ₂ ) + ⁺ A 4 ( 1 ^{- y - k} 3 )

^B1 ^k1 ^{+ B} 2 ( У ^{- k} 2 ^{- k} 1 ) ^{+ B} 3 ( ^k 3 ^{+ k} 2 ) ^{+ + B} 4 ( 1 ^{- y - k} 3 )

+ [ ( A 2 - A 4 ) X + ( B 2 - B 4 ) U Jy =

= M 1 x + M ₂ u + M ₃ y ,

"C1 k1 + C2 (y - k2 - k1) + C3 (k3 + k2) +

^_ _+ C 4 ( 1 -y- k 3 )

u +

D 1 k 1 + D ₂ ( y - k ₂ - k 1 ) + D ₃ ( k ₃ + k ₂ ) + + D 4 ( 1 ^{- y - k} 3 )

+ [ ( C 2 - C 4 ) X + ( D 2 - D 4 ) U Jy =

= M ₄ x + M 5 u + M 6 y .

u +

Применим преобразование Лапласа к системе уравнений:

sx = M,x + M₂u + M ₃ y, I

_ L 2_     3 r (9)

y = M ₄ x + M 5 u + M 6 y .

Решим систему уравнений относительно y :

y = M ₄ [ sE - M 1 ]^{- 1} [ M ₂ u + M ₃ y ] + M 5 u + M 6 y . (10)

Из этого выражения можно получить передаточную функцию (ПФ):

W ( s ) = y

У u = 0

= M ₄ [ sE - M 1 ] - 1 M ₃ + M 6 .

Найдем значение матриц,

ченном выражении:

M 1 =

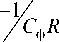
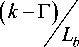
используемых в полу-

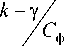
M3 =

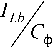
^^^^^^в

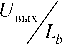
к = 1 — кз + к =1 —

arccos ( a ) + СД _вых

® экв         I вх

M 4 = [ 1 0 ] , M 6 = [ 0 ] ,    (12)

1 — Л—РZ2— (1+a)x Lp 1 + Lp 2^

arccos ( a ) — arccos ( P ) ^

.           ®экв            ,

T П

Подставив (12) в (11), получим ПФ:

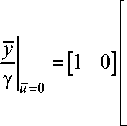
s

—(k—y)

к — y

C ф

⁺ c R

s

+ v +И2£ C ф R н    L b C ф

^— I Lb C ф

Lb _

L b      U вых

1 — s---------7 ----Rн (к — y)2 J k — y

^L b ^C ф, + s____L b - + 1

(k — y)     RH (k — y)

W nH ( V ) = K пн

L р 1 I вх ^U вых

¹ ^ НФ ^v т Кз s ² + 2 ^ Т кз v + 1,

где

U вых             L b

=       ; ⁷НФ =

k — y        Rh (к — y)

PbC^; E =. ^ (к — y)2      2R •(к—y) ^cф

Для обеспечения стабилизации выходного напряжения необходимо ввести контур отрицательной обратной связи. На рис. 3 показаны варианты структурных схем стабилизатора напряжения с одноконтурным (рис. 3, а ) и двухконтурным (рис. 3, б ) способом управления.

Для обеспечения устойчивости системы в нее введено корректирующее устройство (КУ). На рис. 4 представлены частотные характеристики до введения корректирующего устройства и после. В данном случае в качестве КУ используется пропорционально-интегро-дифференцирующий регулятор [1].

б

Рис. 3. Структурная схема ИСН с одноконтурным ( а ) и двухконтурным ( б ) способом управления

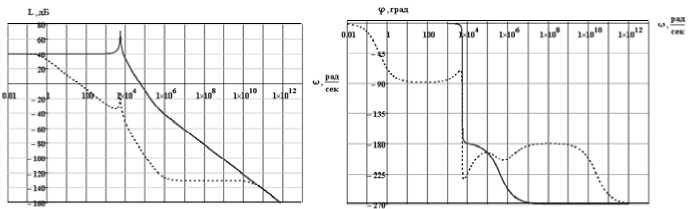
Рис. 4. Частотные характеристики ИСН

Для оценки качества регулирования было проведено численное моделирование в пакете Micro-Cap 9.0. На рис. 5 показаны переходные процессы выходного напряжения при изменении выходной мощности от 150 до 300 Вт при U ВХ = 50В ПНТ-преобразователя и классического преобразователя. Из рис. 5 видно, что ПНТ-преобразователь имеет больший коэффициент демпфирования по сравнению с классическим преобразователем при данном способе управления.

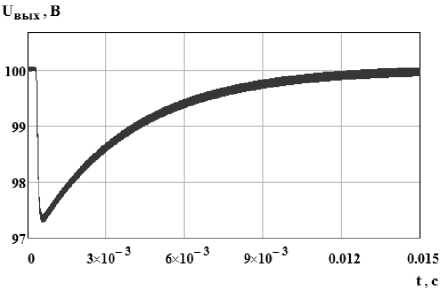
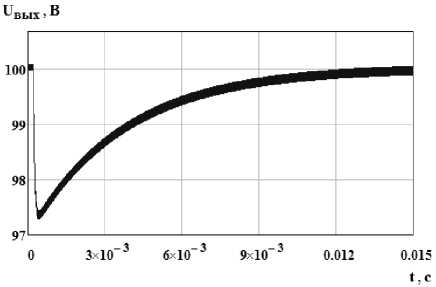
Для улучшения качества управления введем местную обратную связь по среднему току дросселя [6], как показано на рис. 3, б . Из рис. 6 видно, что при данном способе управления переходные процессы классического и ПНТ преобразователя существенно не отличаются и отклонение от заданного напряжения составляет менее 3 %.

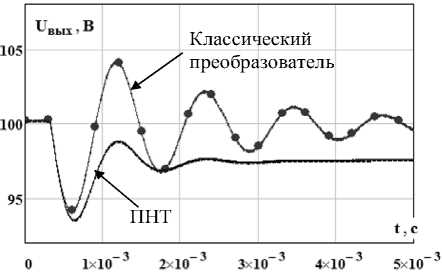
Рис. 5. Переходной процесс выходного напряжения при изменении выходной мощности от 150 до 300 Вт

а

б

Рис. 6. Переходной процесс выходного напряжения при изменении выходной мощности: а – классический преобразователь; б – ПНТ-преобразователь

Так как на входе реального преобразователя стоит солнечная батарея (СБ), которая является нелинейным источником тока с ненулевой выходной емкостью, то динамический анализ далее будем проводить, заменив идеальный входной источник напряжения моделью СБ.

Вольт-амперная характеристика СБ описывается следующим уравнением:

I(U ) = I к.з ( 1 + e f ⁽ U ) ) ,             (17)

где f (U) =

( U - U хх ) ln(1 - i )

U хх ( j - 1 )     ;

|опт; j = Uonm, (18) IКЗ      Uхх здесь IКЗ – ток короткого замыкания СБ; Uхх – напряжение холостого хода СБ; Iопт, Uопт – ток и напряжение в оптимальной рабочей точке. Выбираем следующие значения параметров СБ: Iк.з = 7,5А, Uхх = 80 В, Iопт = 6А, Uопт = 70 В, С = 1 мкФ.

На рис. 7 показан переходной процесс выходного напряжения при изменении выходной мощности от 150 до 300 Вт и моделью СБ в качестве первичного источника. Сравнивая переходные процессы на рис. 6 и 7, можно сделать вывод, что замена СБ источником напряжения не оказывает заметного влияния на динамику системы.

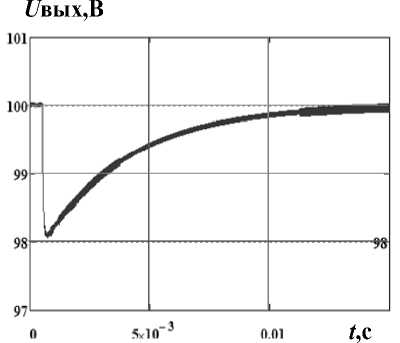
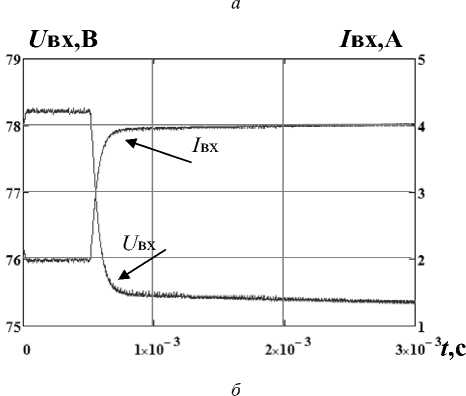
Рис. 7. Переходные процессы выходного напряжения ( а ) входного напряжения и входного тока ( б )

На рис. 8 показаны диаграммы токов через индуктивности РК и напряжений на ключах имитационной модели преобразователя, построенной в пакете схемотехнического моделирования Micro-Cap 9.0, а на рис. 9 показаны их экспериментальные осциллограммы. Высокая степень совпадения формы и параметров сигналов в силовой части ПН за один цикл преобразования подтверждает адекватность имитационной модели, а значит и правомерность ее использования для анализа динамических режимов ПН данного типа.

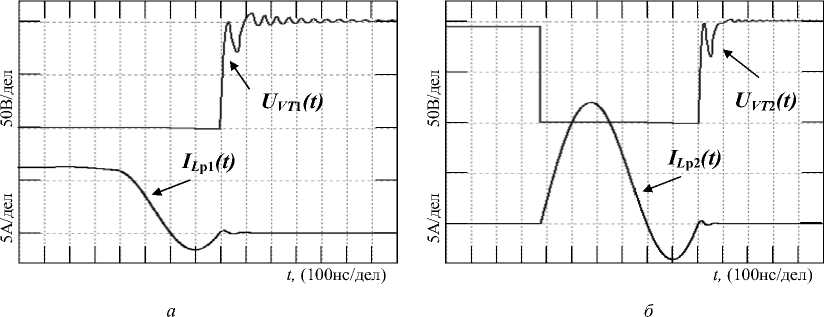
Рис. 8. Диаграммы токов через индуктивности РК и напряжений на ключах

U vt i (t)

^U VT2 ^(t)

I l pi ^(t)

t, (150нс/дел)

а

Рис. 9. Осциллограммы токов через индуктивности РК и напряжений на ключах

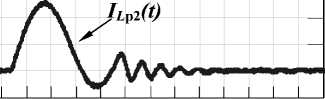
t, (150нс/дел)

б

Результаты моделирования показали, что резонансный контур увеличивает коэффициент демпфирования системы. При одноконтурном регулировании колебательность переходных процессов значительно меньше по сравнению с классическим ШИМ преобразователем при прочих равных условиях. Двухконтурный способ управления не дает существенной разницы между исследуемым ПН и традиционным. Это позволяет применять оба способа регулирования для предлагаемого ПН.