Исследование предельного среднеквадратичного отклонения рабочей поверхности зонтичной антенны от параболоида вращения

Рассмотрена математическая модель рабочей поверхности антенны, зонтичного вида для двух вариантовупру-гих параметров сетеполотна. В первом варианте сетеполотно имеет нулевую жесткость в направлении меридиана, а во втором - нулевую жесткость в окружном направлении. Получены аналитическиезависимости, позволяющие оценить предельные среднеквадратичные отклонения поверхности зонтичной антенны от параболоида.

При проектировании зонтичной антенны значительную роль играет оценка точности рабочей поверхности, которую образует сетеполотно, натянутое на радиальные ребра. Материал сетеполотна гибок, является упругим и после раскрытия и натяжения антенны формирует отражающую поверхность.

Сетеполотно, натянутое на два смежных ребра, образует лепесток антенны. Профиль ребра представляет собой параболу, а поверхность, проходящая через все ребра, является параболоидом вращения. Реальная рабочая поверхность лепестка антенны имеет седлообразную форму, т. е. по меридиану она выпукла, а по окружности - вогнута.

В качестве критерия точности реального профиля антенны рассматривается среднеквадратичное отклонение рабочей поверхности антенны от параболоида вращения, которое является одним из критериев совершенства поверхности антенны, характеризующим ухудшение свойств поверхности сетеполотна при его натяжении. Определение среднеквадратичного отклонения было выполнено в работах [1...4], и в качестве модели сетеполотна в этих исследованиях рассматривалась мембрана, деформирование которой описывалось уравнением Лапласа.

В данной статье определение среднеквадратичного отклонения выполняется без анализа напряженно-деформированного состояния сетеполотна. Рассматривается модель отражающей поверхности антенны для двух предельных вариантов упругих параметров сетеполотна. В первом сетеполотно имеет нулевую жесткость в направлении меридиана, а во втором - нулевую жесткость в окружном направлении.

Пусть теоретический профиль антенны (рис. 1) определяется уравнением параболоида z = c(х1 + У2), (1) r2

где с - высота параболоида; г - внешний радиус параболоида.

лись под углом ф = 2п / п , где п - количество ребер антенны.

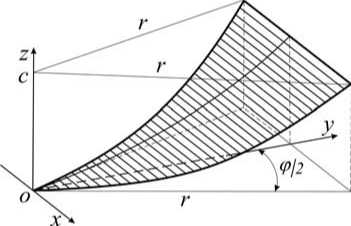
Рис. 2. Лепесток антенны, сетеполотно которого имеет нулевую жесткость в радиальном направлении

Параболоид является двояковыпуклой поверхностью, поэтому наилучшее приближение параболоида достигается в случае, когда кривизна сетеполотна в окружном направлении равна нулю. Иными словами, идеальным является сетеполотно, которое имеет нулевую жесткость вдоль меридиана параболоида. Очевидно, что в этом случае реальная поверхность лепестка антенны будет образована прямыми, параллельными плоскостям хОу и xOz и соединяющими ребра жесткости (см. рис. 2). Поверхность лепестка является параболическим цилиндром. Сечение этого цилиндра плоскостью xOz представляет собой параболу

z = ky2, (2)

где к - неизвестный параметр. При z = с , у = г cos ф /2. Тогда для параметра к будем иметь

r ² cos² ф /2 , Подставляя (3) в (2), получим

c z = ^---2----У .

r cos ф /2

Уравнение (4) определяет поверхность лепестка ан

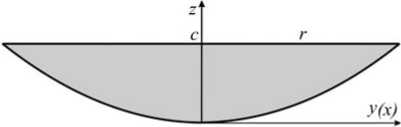
Рис. 1. Теоретический профиль антенны

тенны для случая, когда сетеполотно имеет нулевую жесткость в радиальном направлении (рис. 3).

Определим среднеквадратичное отклонение поверхности лепестка антенны (4) от поверхности параболоида (1) следующим функционалом:

w ₁

ab

ab

2 JJ

S

0 0 _

СУ²        c . Г

—---2     —2 (х + У ) dxdy . (5)

r cos ф /2 r

Расположим на параболоиде два радиальных ребра жесткости симметрично относительно оси Оу (рис. 2) так, чтобы проекции ребер на плоскость хОу пересека

Где У = г ² sin ф / 2 cos ф / 2 - площадь проекции поверхности лепестка на плоскость хОу ; а = г cos ф / 2, Ъ =у tg ф / 2. Выполняя в (5) интегрирование и необходимые преобразования, получим

2V2 . 2 Ф

• w, = —ci sin — .             (6)

• ¹    35     2

2 . Ф Ф r2 sin cos

Уравнение (6) определяет среднеквадратичное отклонение поверхности антенны от параболоида для случая, когда сетеполотно обладает жесткостью только в кольцевом направлении. Отметим, что полученное значение w _t - это предельное, не улучшаемое среднеквадратичное отклонение для параболической антенны зонтичного типа.

z = с

,           Фх/ .    • Фх

( у - r cos 2)( X + r sin 2)

Уравнение (9) описывает форму поверхности лепестка антенны для случая, когда сетеполотно имеет нулевую жесткость в окружном направлении (рис. 5).

Рис. 3. Антенна, сетеполотно которой имеет нулевую жесткость в радиальном направлении

Рис. 5. Антенна, сетеполотно которой имеет нулевую жесткость в окружном направлении

Рассмотрим второй предельный вариант упругих параметров сетеполотна. Будем полагать, что материал се-теполотна имеет нулевую жесткость в окружном направлении. Соединим внешние концы ребер антенны в раскрытом состоянии хордой (рис. 4). Поверхность лепестка антенны в этом случае будет образована отрезками прямых, соединяющих ребра с хордой и расположенных в плоскостях параллельных плоскости уОz .

Определим среднеквадратичное отклонение поверхности лепестка антенны (9) от поверхности параболоида (1) в виде функционала

ab

ab

III с 1 +

^ 0 0

,          Фх/ .    • Фх

( У - Г cos -2)( X + Г sin 2)

2 • Ф Ф r2 sin cos

^^^^в

4⁽ x ² + у ²⁾ dxdy .(10)

Здесь по-прежнему 5 = г ² sin ф / 2cos Ф /2- площадь проекции поверхности лепестка на плоскость хОу , а = г cos Ф / 2, b =у tg Ф / 2. После преобразований будем

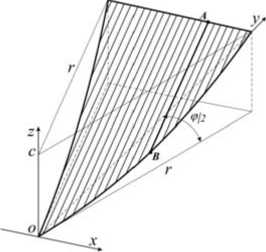
Рис. 4. Лепесток антенны, сетеполотно которого имеет нулевую жесткость в окружном направлении

Получим уравнение поверхности лепестка. Из-за симметрии поверхности относительно плоскости уОz будем рассматривать только половину лепестка, т. е. область, у которой х> 0. Для вывода уравнения поверхности воспользуемся каноническим уравнением произвольной прямой ЛВ , проходящей через две точки:

У - У 1 ₌ z - z i ,

У 2 - У1 z 2 - zi гдеуt, zt - координаты точкиЛ, лежащей на стержне, со единяющем концы ребер, у2, z2 - координаты точки В, лежащей на ребре. В случае, представленном на рис. 4,

Ф         . Ф                X 2 «   . 2фх /ОХ

У 1 = X cos -^, у 2 = X ctg -^, z = с ^, z ₂ = с — (1 + ctg ;Ч. ⁽⁸⁾

2            2                r2

Подставляя (8) в (7), найдем иметь

• w2 = —c= 222-37cos2 Ф + 16cos4 Ф .(11)

• 2    310           22

Уравнение (11) определяет максимальное (наихудшее) среднеквадратичное отклонение поверхности антенны от параболоида для случая, когда сетеполотно обладает жесткостью только в радиальном направлении.

Проведем анализ формул (6) и (11). Учитывая, что Ф / 2 = п / п , где п - число ребер, запишем уравнения (6) и (11) в следующем виде:

2^2 . 2 — w1 = —5 с sin — , w2 = —c= ./22 - 37cos2 — + 16cos4 —.     (12)

• ²    310            n n

По выражению (12) следует, что при п ^ ^ величина wt ^ 0, а w2 ^ с / (3 V10). 3начения относительных отклонений wt / с и w2 / с для различных п приведены в таблице и на рис. 6, где число ребер п рассматривалось как непре рывная переменная.

Таким образом, в данной статье определены границы среднеквадратичного отклонения отражающей поверхности антенны от параболоида вращения. Очевидно, что отклонение поверхности реальной антенны будет находиться между предельными среднеквадратичными отклонениями. Анализ полученных результатов позволяет так- же сделать вывод о том, какие упругие параметры должно иметь сетеполотно антенны. Минимальное отклонение может быть получено тогда, когда материал сетепо-лотна обладает ярко выраженной ортотропией упругих характеристик: нити основы тканого сетеполотна долж

n	W [ / c	W 2 / c	n	W [ / c	W 2 / c
6	0,105 409	0,190 029	22	0,008 540	0,110 947
8	0,061 747	0,151 854	24	0,007 183	0,110 042
10	0,040 263	0,134 303	26	0,006 126	0,109 343
12	0,028 244	0,125 021	28	0,005 286	0,108 791
14	0,020 878	0,119 574	30	0,004 607	0,108 348
16	0,016 048	0,116 117	32	0,004 051	0,107 987
18	0,012 714	0,113 789	34	0,003 590	0,107 689
20	0,010 318	0,112 148	36	0,003 203	0,107 440