Исследование применимости метода конечных элементов для оценки параметров механики разрушения конструктивных элементов из композиционных материалов

нагружения, различной конфигурации и различных физических свойствах рассматриваемого элемента, исследовать поведение конструктивных элементов сложной геометрии.

Цель работы: нахождение интенсивности освобождения энергии при разрушении композитной панели с центральной трещиной с использованием МКЭ и сравнение полученного результата с имеющимся в литературе аналитическим решением.

Рассматривается сквозная трещина в композиционном материале, располагающаяся параллельно волокнам и нагруженная растягивающими нагрузками. Такая трещина называется трещиной расслаивания, при этом расслоение происходит не между отдельными слоями материала, а в плоскости самой пластины. Такого рода расслоение также называется внутрислой-ным растрескиванием. Решение поставленной задачи рассмотрено в статье [1]. Оно основывается на понятии скорости высвобождения энергии или интенсивности высвобождения упругой энергии. Ранее аналитическое решение было получено и рассмотрено Ирвином, Пэрисом и Си в статье [2]. В соответствии со статьёй [1] интенсивность освобождения упругой энергии для композиционного (ортотропного) материала для мод I и II определяется следующими выражениями:

G, = К? (°^

<5|с:..!

-11

05 + 201? + 06610,5

2o 11

G,, = K,^[(^f +

V2 [ °Ow’

2012 + 066

-10,5

■1

>

>

где a ij - элементы матрицы податливости однонаправленного композита (ось 1 направлена вдоль трещины, т.е. в направлении волокон), К ] , К_]] -коэффициенты интенсивности для мод I и II соответственно.

В рассматриваемой задаче будет реализовано нагружение только по моде I (отрыв). В статье [3] подобная задача рассматривается с точки зрения нахождения коэффициентов интенсивности напряжений (КИН) в виде:

К] = аЛ • Y, где l - полудлина трещины, а - напряжения растяжения, Y – поправочный коэффициент, учитывающий конечность размеров пластины.

Следует отметить, что использование КИН, взятых из справочников для изотропных материалов, неприемлемо. Они могут быть использованы лишь для квазиизотропных композиционных материалов.

При выполнении численного расчёта в пакете ANSYS благодаря двойной симметрии можно ограничиться рассмотрением лишь четверти пластины. Для вычисления интенсивности освобождения энергии на этапе разбиения сеткой конечных элементов (КЭ) полученной геометрической модели необходимо создавать в вершине трещины сингулярную сетку элементов для правильного описания напряжённо-деформированного состояния у вершины трещины. Последнее реализуется в пакете ANSYS заданием точки концентрации (Concentrate KP). В качестве граничных условий в данной задаче задаются растягивающие напряжения, действующие на пластину. На левой и нижней кромке задаются условия симметрии, исключая при этом на нижней кромке узлы, лежащие на берегах трещины. Материал панели – углепластик. Параметры, характеризующие физические свойства материала панели: модули упругости Е 1 = 1,448 • 10⁵ МПа, Е 2 = 1,172 • 10⁴ МПа; модуль сдвига G ₁₂ = 9,653 • 10³ МПа; модуль Пуассона д ₂₁ = 0,21. Здесь ось 1 направлена вдоль волокон, а ось 2 перпендикулярно им. Для вычисления интенсивности освобождения энергии в пакете ANSYS используется встроенная команда CINT (тип команды VCCT), основанная на применении метода виртуального раскрытия трещины. В соответствии с ним:

G ]

—

EV RyДv, 2Да у где Ди - относительное смещение между верхними узлами трещины в локальных координатах y, Ry - реакция в вершине трещины, Да - размер элемента как показано на рис. 1.

Для автоматизации процесса генерации конечно-элементной модели составлен макрос, позволяющий рассчитывать интенсивность освобождения энергии для разной конфигурации панели и длины дефекта. Схема панели с трещиной приведена на рис. 2. На рис. 3 представлена сетка сингулярных элементов в вершине трещины. Расчёты проводились для различной конфигурации панели (h, b – высота и ширина пластины соответственно), различной прикладываемой нагрузки и различных длин трещин.

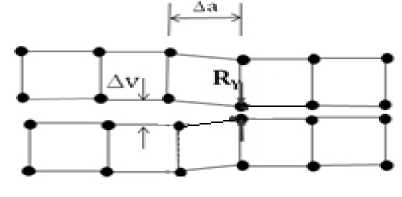
Рис. 1. Метод виртуального раскрытия трещины

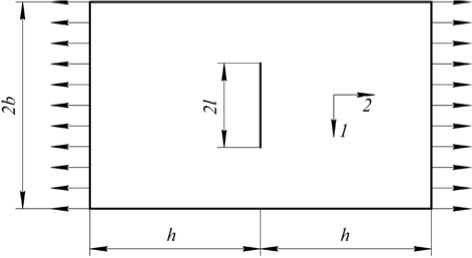
Рис. 2. Схема панели с трещиной

Рис. 3. Сингулярная сетка элементов в вершине трещины

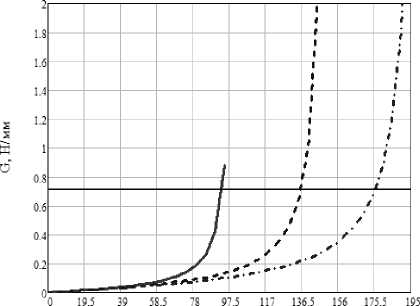
Из рис. 4 видно, что при увеличении длины трещины интенсивность освобождения энергии возрастает. По рис. 5 можно судить о том, что при увеличении прикладываемых напряжений интенсивность освобождения энергии также возрастает. Зная критическое значение интенсивности освобождения энергии (вязкость разрушения) можно сказать, при каком значении длины трещины, прикладываемых напряжений в зависимости от конфигурации рассматриваемого элемента произойдёт разрушение объекта. Для связующего ЕР-1210 вязкость разрушения составляет 0,71 Н/мм. На рис. 6 приведены аналитические значения, после сравнения которых с МКЭ-расчётом можно сказать, что погрешность менее 5%.

L мм

---КЪ=3

— №=2

-.-h/b=L5

---Glc

Рис. 4. Зависимость интенсивности освобождения энергии от полудлины трещины

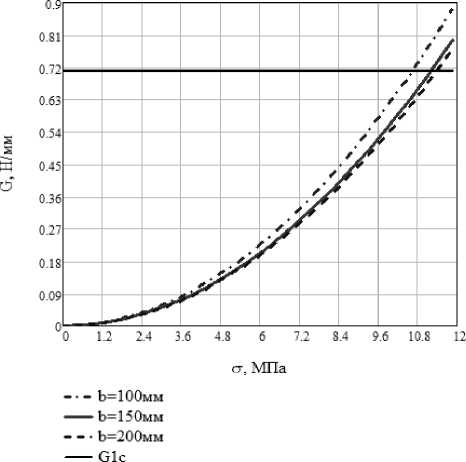
Рис. 5. Зависимость интенсивности освобождения энергии от прикладываемых напряжений

Реальные конструкции из композиционных материалов могут иметь подкрепления, которые оказывают существенное влияние на напряжённо-деформированное состояние и значение параметров трещиностойкости. Поэтому в данной работе рассмотрено влияние продольного подкрепления панели на интенсивность освобождения энергии. В качестве подкреплений композиционной панели взяты стальные пояса с площадью поперечного сечения 380 мм2. По рис. 7 можно судить о том, что подкрепление панели значительно снижает интенсивность освобождения энергии, что в свою очередь увеличивает несущую способность панели. При этом моделирование подкрепления выполнялось с помощью линейного конечного элемента с заданием его жёсткости на растяжение (сжатие) по формуле:

EF

2h

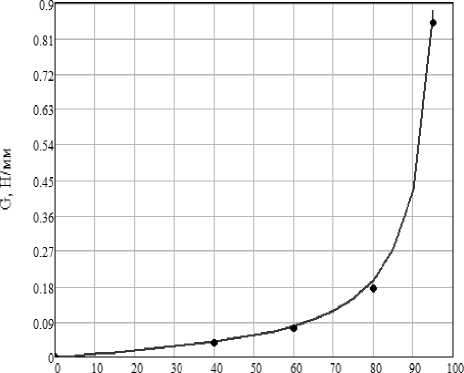
L мм

— МКЭ

• ••• Теория

Рис. 6. Сравнение аналитических и численных расчётов

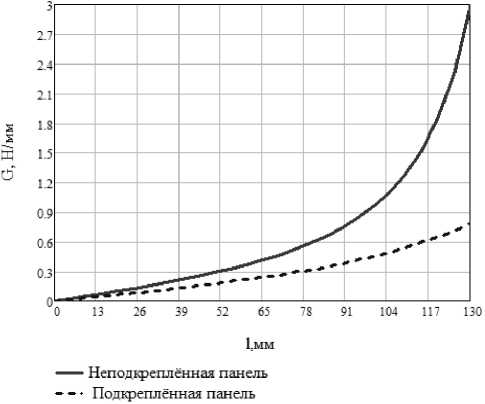
Рис. 7. Зависимость интенсивности освобождения энергии от длины трещины

Выводы: рассмотрено влияние конфигурации панели, а также длины дефекта на параметр механики разрушения. Показано, что подкрепление панели значительно снижает интенсивность освобождения энергии. МКЭ с достаточной для инженерных расчётов точностью позволяет рассчитывать параметры механики разрушения без каких-либо значительных ограничений.