Исследование применимости модели основания Винклера для описания контактного взаимодействия упругопластических оболочек с заполнителем при внешнем давлении
Автор: Баженов В.Г., Нагорных Е.В., Самсонова Д.А.
Статья в выпуске: 4, 2020 года.
Бесплатный доступ
Задача деформирования и упругопластического выпучивания оболочек вращения с толстостенным упругим заполнителем при комбинированных статических и динамических нагружениях формулируется в плоской двумерной постановке исходя из двух подходов: полномасштабное моделирование в рамках механики сплошных сред и упрощенная постановка, основанная на гипотезах теории оболочек типа Тимошенко и основания Винклера. Оба подхода позволяют решать задачи деформирования и устойчивости непологих оболочек с учетом геометрических нелинейностей. Постановка с позиций механики сплошных сред позволяет аппроксимировать оболочку и заполнитель по толщине рядом слоев конечных элементов. Определяющие соотношения формулируются в переменных Лагранжа с использованием в качестве отсчетной неподвижной декартовой системы координат. Кинематические соотношения записываются в метрике текущего состояния. Упругопластические свойства оболочек описываются теорией пластического течения с изотропным упрочнением. Уравнения движения следуют из баланса виртуальных мощностей работ. В первом подходе контактное взаимодействие оболочки и упругого тела моделируется условиями непроникания по нормали и свободного проскальзывания вдоль касательной. Условия непроникания выполняются только в активной фазе контактного взаимодействия, при нарушении контакта они заменяются условиями на свободной поверхности. Во втором подходе контактное взаимодействие упругого заполнителя с оболочкой моделируется основанием Винклера. Оба подхода позволяют описать нелинейное докритическое деформирование оболочек вращения с упругим заполнителем, определить предельные (критические) нагрузки в широком диапазоне скоростей нагружения с учетом геометрических несовершенств формы. С применением обоих подходов выполнено численное моделирование задачи контактного взаимодействия упругопластической цилиндрической оболочки с толстостенным упругим заполнителем при квазистатическом равномерном внешнем давлении. Проведено исследование влияния толщины и начальной погиби оболочки, а также жесткости и толщины заполнителя на величину критического давления и формы потери устойчивости. На основании этих расчетов сделан вывод о широкой области применимости модели основания Винклера.
Цилиндрическая оболочка, толстостенный упругий заполнитель, внешнее давление, упругопластическое выпучивание оболочки, основание винклера, численное моделирование, метод конечных элементов
Короткий адрес: https://sciup.org/146282024
IDR: 146282024 | УДК: 539.3 | DOI: 10.15593/perm.mech/2020.4.04
Текст научной статьи Исследование применимости модели основания Винклера для описания контактного взаимодействия упругопластических оболочек с заполнителем при внешнем давлении
ВЕСТНИК ПНИПУ. МЕХАНИКА № 4, 2020PNRPU MECHANICS BULLETIN
The problem of deformation and elastoplastic buckling of shells of revolution with a thickwalled elastic core under combined static and dynamic loading is formulated in a two-dimensional planar formulation based on two approaches: full-scale modeling within continuum mechanics and a simplified formulation based on the hypotheses of the theory of shells of the Timoshenko type and the Winkler foundation. Both approaches allow solving the problems of deformation and stability of non-shallow shells on the basis of Timoshenko's hypotheses, taking into account geometric nonlinearities. The statement from the perspective of continuum mechanics makes it possible to approximate the shell in thickness by a number of layers of finite elements. The constitutive relations are formulated in Lagrange variables using a fixed Cartesian coordinate system as a reference one. Kinematic relations are recorded in the metric of the current state. The elastic-plastic properties of shells are described by the theory of plastic flow with isotropic hardening. The equations of motion follow from the balance of the virtual powers of the work. In the first approach, the contact interaction of a shell and an elastic body is modeled by the conditions of nonpenetration along the normal and free slip along the tangent. The nonpenetration conditions are satisfied only in the active phase of the contact interaction; if the contact is broken, they are replaced by conditions on the free surface. In the second approach, the contact interaction of the elastic core with the shell is modeled by the Winkler foundation. Both approaches allow one to describe the nonlinear subcritical deformation of shells of revolution with an elastic core, to determine the limiting (critical) loads in a wide range of loading rates, taking into account the geometric imperfections of the shape. Using both approaches, a numerical simulation of epy contact interaction problem of an elastoplastic cylindrical shell with a thick-walled elastic core at a quasi-static uniform external pressure is carried out. The study of the influence of the thickness and initial deflection of the shell, as well as the stiffness and thickness of the core, on the value of the critical pressure and the form of buckling has been carried out. Based on these calculations, a conclusion was made about a wide range of applicability of the Winkler foundation model.
Для увеличения запаса устойчивости оболочечных конструкций и блокирования неосесимметричных форм выпучивания применяется внутренний заполнитель [1–20]. В теоретических исследованиях деформирования и устойчивости оболочек упругий заполнитель описывается уравнениями теории упругости [3, 6, 9, 10, 14, 20] или моделируется упругим основанием с одним или двумя коэффициентами постели (основание Винклера или Пастернака) [5–8, 12, 15, 17–19]. Подробный обзор экспериментальных и численных исследований по определению напряженно-деформированного состояния и устойчивости тонких оболочек с заполнителем приведен в [6]. Наличие заполнителя повышает критические нагрузки и существенно влияет на формообразование оболочки на закритической стадии деформирования. Например, при осевом сжатии круговых цилиндрических упругопластических оболочек с заполнителем образуются кольцевые складки, т.е. сохраняется осесимметричная форма потери устойчивости [1, 2]. При осевом нагружении пустотелых оболочек происходит трансформация осесимметричной формы потери устойчивости в неосесимметричную [1, 21]. Современные возможности вычислительной техники позволяют решать задачи устойчивости оболочек при пластических деформациях, учитывая геометрическую и физическую нелинейности, краевые эффекты и начальные несовершенства при произвольных комбинациях видов нагружения. В ходе решения вычисляются докритические формоизменения конструкций и предельные, а не бифуркационные нагрузки. Работы [2, 22, 23] посвящены численным решениям осесимметричных геометрически нелинейных упругопластических задач деформирования и устойчивости металлических оболочек при квази-статических и динамических нагружениях с малыми деформациями и немалыми перемещениями. Динамическая постановка задачи дает возможность моделировать закритическое поведение упругопластических конструкций – перескок к новым равновесным состояниям. Выбор эффективной модели конечного элемента и параметров дискретизации тонкостенных конструкций является нетривиальной задачей [24].
Целью настоящей работы является оценка области применимости модели Винклера для задачи деформирования и потери устойчивости упругопластических цилиндрических оболочек с толстостенным упругим заполнителем. Численное моделирование процессов осуществлялось в плоской двумерной постановке в рамках двух подходов: полномасштабное моделирование в рамках механики сплошных сред и упрощенная постановка, основанная на гипотезах теории оболочек типа Тимошенко и основания Винклера. Применяемые методы исследования позволяют описать нелинейное докритиче-ское деформирование оболочек вращения с упругим заполнителем, определить предельные (критические) нагрузки в широком диапазоне скоростей нагружения с учетом геометрических несовершенств формы.
1. Методика численного решения двумерных задач в плоской постановке в рамках механики сплошных сред
Полная система механических уравнений, описывающих динамическое деформирование сплошной среды в условиях плоской или осесимметричной деформации, записывается в декартовой Orz или цилиндрической системе координат Or р z ( Oz - ось вращения).
Кинематические соотношения формулируются в скоростях и строятся в метрике текущего состояния. Компоненты тензоров скоростей деформаций и скоростей вращения имеют следующий вид:
e = u ё„„ = nit,r-1, e = U , rr r,r , pp r , zz z,z , e„ = 4 Zu,, + it,,, 6),, =1 Zu,, - it,,). zr 2 \ z, r r, z / , zr 2 \ z, r r, z /
Уравнение движения сплошной среды следует из уравнения баланса виртуальных мощностей:
jj (о rr 8 err +W§ epp + ozz 8 ezz + 2° rz 8 erz ) rn d Q + Q
+ jj(pwr8ur + pwz8uz) rndQ-
Q
- j ( pr 8 u r + pz 8 u z ) r n dG - j ( q r 8 U r + q z 8 U z ) r n dG = 0. (2) G p G q
Здесь n — параметр симметрии (n = 0 - плоская деформация, n = 1 — осесимметричная деформация); Q = J Q k - область, занимаемая сплошной средой на k плоскости Orz (n = 0 ) или в меридиональном сечении
(n = 1); Gp = J(Gp) — часть поверхности, на которой kk задается априори известная поверхностная нагрузка;
Gq = U (Gq) — часть поверхности, на которой задаются kk контактные давления, определяемые в процессе решения, к = 1, D ; D - количество деформируемых тел; oj и eij - компоненты тензоров напряжений Коши и скоростей деформаций (симметричной части градиента скорости перемещений); Ua и wa - компоненты векторов скорости перемещения и ускорения перемещения; pa и qa - компоненты поверхностных и контактных нагрузок (i, j, a = r, в, z); p - плотность.
Для описания упругопластических свойств материалов применяется теория течения с нелинейным изотропным упрочнением. Связь между компонентами девиатора скоростей напряжений 0 j = 6 j + P 8 j и упругими составляющими компонент девиатора скоростей деформаций ( e j ) = e j - e 8 j /3 - e p осуществляется на основе обобщенного закона Гука в метрике текущего состояния:
j
D J о j j = 2 G ( ej ) , D J o i j o j j 6o kj -<» jk oi k , (3)
p =- Kee , p = -ou /3, e = e e , ep = 0.
Здесь K , G - модули объемного сжатия и сдвига; P - давление; D J - производная Яуманна, учитывающая поворот частицы среды как жесткого целого; 8 j -символ Кронеккера.
Уравнение поверхности текучести, ограничивающей в пространстве девиаторов напряжений область упругих состояний, принимается в форме Мизеса. Скорости пластических деформаций определяются ассоциированным законом течения:
t ep = /ojj, ojoj = 23o (»), $ = 72/3 j jdt. (4)
Компоненты контактного давления q r , q z , входящие в уравнение движения (2), определяются в ходе решения задачи из условий непроникания по нормали и свободного проскальзывания вдоль касательной. На контактных границах ( Gq ) вводится местный координатный базис s , ^ , связанный с деформированной поверхностью. Здесь s и ^ - направления касательной и нормали к поверхности. Усилие по нормали определяется из условия непроникания, а касательные усилия полагаются равными нулю:
u ^ = u ^
/ »
q I; =- q I; .
[ 0, q E > 0
;
q ; = q ; =) n q s = q s = 0. (5)
^ q ; , q ; < 0,
Функции со штрихом относятся к первой контактирующей поверхности, с двумя штрихами - ко второй. Связь контактирующих тел полагается односторонней, т.е. возможен отрыв поверхностей друг от друга и повторное вступление в контакт. Поэтому условия (5) применяются только для сжимающих усилий. Контактные усилия определяются с использованием симметричного алгоритма на несогласованных разностных сетках [25, 26].
Система уравнений (1)-(5), дополненная кинематическими граничными и начальными условиями, решается методом конечных элементов в сочетании с явной схемой интегрирования типа «крест» [27].
-
2. Методика численного решения двумерных задач в плоской постановке, основанная на гипотезах теории оболочек типа Тимошенко и основания Винклера
Задача деформирования и упругопластического выпучивания оболочек вращения с заполнителем при комбинированных статических и динамических нагружениях формулируется в двумерной (плоской или осесимметричной) постановке на основе методики [21]. Определяющая система уравнений записывается в декартовой (или цилиндрической) системе эйлеровых координат Orz ( Oz - ось вращения). Для каждого оболочечного элемента вводится местная лагранжева система координат Os — , связанная с общей соотношениями ds = у z dr - у r dz , d — = у r dr + у z dz , где s - длина дуги меридиана оболочечного элемента; — - координатная линия, нормальная к срединной поверхности; у z = rs , у r = - zs - направляющие косинусы нормали к срединной поверхности.
Оболочечные элементы полагаются тонкими, метрика по толщине не меняется. Кинематические соотношения формулируются в скоростях и строятся в метрике текущего состояния:
Us (s,—, t) = Us (s, t) + —0s (s, t), ii- (s, —, t) = u- (s, t), eii = eii + —Xii, i = s,e es— e0— (1 -(2-h)2), ess=es—= °,
£ 0 = u ш V 7 ,
55 r , 5T2 zs , s i r , x 55 Ф , s ,
, Zpp=nифуzr , e 0— = 2 ( и‘ф+ U r, s У r + Uz, s Vz ) .
Здесь Uis ( s , t ) , U — ( s , t ) - скорости перемещений срединной поверхности в направлении касательной и нормали; й ф ( s , t ) - угловая скорость поворота поперечных сечений в плоскости меридионального сечения; Ё 0 , —XU - компоненты скоростей деформаций срединной поверхности и изгиба. Компоненты тензора скоростей деформаций e j представляются в виде суммы упругих Ё j и пластических Ё pp составляющих:
e j = ё j + ё p , e p = 0, i , j = s , —,0. (7)
Компоненты тензоров скоростей напряжений C ij и напряжений оу определяются через скорости упругих компонент деформаций Ё j :
C ss =1 2 ( e ss + Ц e р ) , б рр = , 2 ( e в +Ц e ss ) ,
1 -ц 1 -ц ys — = 1+Ц ee—, п- °. yse = 0 (8)
У = j C j dt , i , j = s , — , 0 .
Учет упругопластических свойств материала оболочки осуществляется в рамках теории течения с нелинейным изотропным упрочнением:
eP = ^«у, «у C'у!jУ' , yjy‘ yT(к), yj =yу-y8у, c = (css + yp)/3, к = 72/3 j jdt.
Здесь C T ( к ) - радиус поверхности текучести; к - параметр Одквиста; 8 у - символ Кронекера; параметр X определяется из условия прохождения мгновенной поверхности текучести через конец вектора догрузки.
Вариационные уравнения движения оболочки выводятся из общего уравнения динамики с учетом принятых гипотез теории оболочек:
[ QVr + Ns Vz ] 8 Uir, s + [ Q у z - Ns у r ] 8 Uiz, s f J j
v 1 N e + M p u r - P r - q r r
8 U i r +
+ M s 8 г1 ф , s + [ M p uz - pz - qz ]8 uz +
> r v ds -
+ Q + v 1 M р у z + J p и ф 8 и ф
- r v [ P r 8 U i r + P z 8 U i z + M 0 8/1 ф ] s = 0 , f = 0. (10)
Здесь Pr , Pz , M 0 - внешние усилия и изгибающий момент, приложенные к контуру оболочки; pr , pz -поверхностные нагрузки; qr , qz - контактные давления; Ns , N р , Q , M s , M p - внутренние усилия и моменты; M p , J p - масса и момент инерции, П -параметр симметрии ( п = 0 - плоская деформация; П = 1 - осесимметричная деформация).
Контакт между оболочкой и деформируемым заполнителем моделируется исходя из условий непрони-кания по нормали и свободного проскальзывания вдоль касательной (5). Функции со штрихом относятся к контактирующей поверхности оболочки, с двумя штрихами – заполнителя. Полагаем, что контактное давление в области взаимодействия оболочки с упругим заполнителем, пропорционально прогибу оболочки (основание Винклера):
q ' ‘ = ku , . (11)
Здесь k – коэффициент пропорциональности (коэффициент «постели»), u ^ ( s , t ) - прогиб контактирующей поверхности оболочки.
В квазистатических задачах скорость нагружения принимается такой, чтобы роль сил инерции была пренебрежимо мала. Система уравнений (6)–(11), дополненная кинематическими граничными и начальными условиями, решается методом конечных элементов в сочетании с явной схемой интегрирования типа «крест» второго порядка точности.
3. Результаты численного моделирования
Решалась задача о потере устойчивости стальных цилиндрических оболочек с упругим толстостенным заполнителем и без него под действием равномерного внешнего давления. При численном моделировании краевые эффекты, вызванные граничными условиями на торцах оболочки, не рассматривались. Полагалось, что оболочка и заполнитель находятся в условиях плоского деформированного состояния. Расчетная область представляет собой поперечное сечение оболочки с заполнителем.
Рассматривались оболочки с двумя вариантами начальной толщины:
h
0
и
h
0/
2, где
h
0
=
1
-
10
-
3
м
, и начальным радиусом
R
0
=
1,45
-
10
-
2 м. Материал оболочек – сталь Х18Н10Т с механическими характеристиками: модуль упругости
E
=
2,1
-
105 МПа, коэффициент Пуассона
ц =
0,3, плотность
р =
7,8
-
10
3
кг/м3, материальная функция модели пластичности приведена в [28]. На внешней поверхности оболочки задавалось квазистатическое нагружение равномерно распределенным давлением с линейным законом изменения во времени:
p
=
p
0
1
(
p0
=
50 МПа/c
)
.
На внутренней поверхности заполнителя задавался запрет перемещений по нормали. Начальные несовершенства оболочки – отклонение поперечного сечения от круглой формы – моделировались начальной погибью срединной поверхности с относительной амплитудой
А
:
A
R
0
=
Ah
0
cos
п
в
, n
=
2,3,..., 0
2
n
.
3.1. Численное моделирование обжатия пустотелой оболочки
Начальная толщина оболочки
h
0 , параметры начальной погиби
A =
1
-
10
-
5 и
n
= 2, так как ожидаемая форма поперечного сечения цилиндрической оболочки после потери устойчивости – эллипс [29]. При моделировании в рамках модели сплошной среды в силу симметрии задачи и с целью уменьшения времени вычислительного процесса в качестве расчетной области рассматривалась половина поперечного сечения оболочки. Расчетная область покрывалась конечно-элементной сеткой с
N
= 5 элементами по толщине и
L
= 60, 120, 160 или 240 элементами вдоль половины окружности. При моделировании в упрощенной постановке расчетная область представляет собой срединную линию поперечного сечения оболочки. Она покрывалась равномерной сеткой с количеством элементов
L
= 120, 240, 320 и 480.
По результатам расчетов определялись зависимости относительного среднего прогиба
w
ˆ от внешнего давления
p
(рис. 1). Относительный средний прогиб оболочки определялся по формуле
1
L
•w
=
t^S
(
u
^
)
,
,
Lh
0
i
=
1
где
(
u
^
)
,
- перемещение по нормали (прогиб) срединной поверхности оболочки в узле сетки с номером
i
.
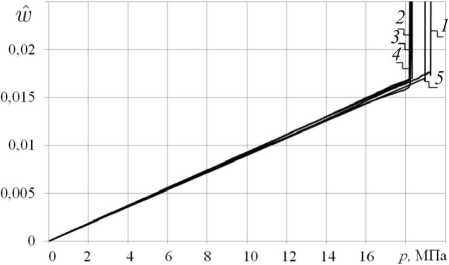
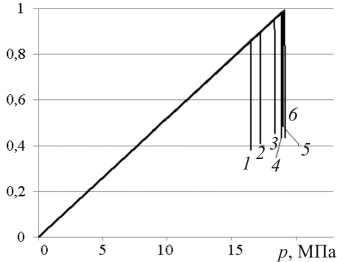
Рис. 1. Зависимости среднего прогиба пустотелой оболочки от внешнего давления:
1–4
– расчеты по модели сплошной среды с
L
= 60, 120, 160 и 240 элементами вдоль половины окружности соответственно; 5 – расчеты по упрощенной модели
Fig. 1. Dependences of the average deflection of the hollow shell on external pressure:
1–4
– are calculations according to the model of a continuous medium with
L
= 60, 120, 160 and 240 elements along half a circle, respectively, 5 shows calculations according to a simplified model
В расчетах момент потери устойчивости оболочки определяется резким ростом относительного среднего прогиба
w
ˆ . Зависимости относительно среднего прогиба оболочки от внешнего давления до момента потери устойчивости оболочек близки к линейным. В расчетах по упрощенной модели разброс критических давлений
p
*, при которых происходит потеря устойчивости, не превышает 0,2 %.
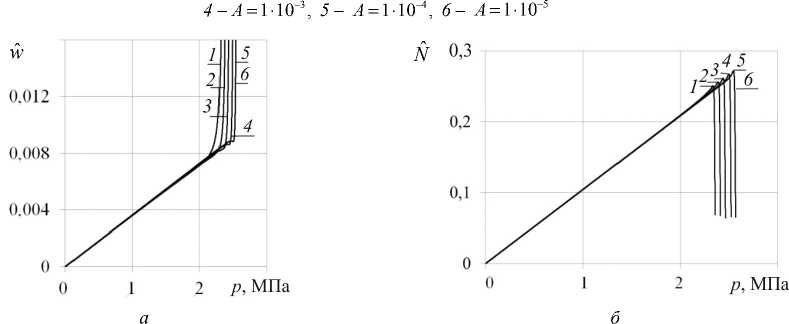
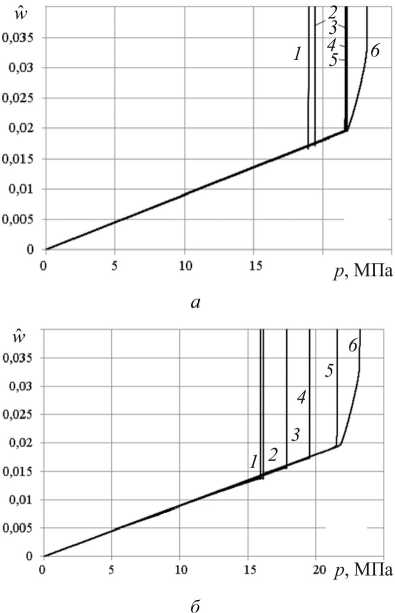
Рис. 2. Зависимости среднего прогиба (
а
) и окружного усилия (
б
) пустотелой упругой оболочки с начальной толщиной
h
0
от внешнего давления при значениях начальной погиби:
1
-
A
=
1
■
10
-
2
,
2
-
A
=
1
■
10
-
3
,
3
-
A
=
1
■
10
-
4
,
4
-
A
=
1
■
10
-
5
Fig. 2. Dependences of the average deflection (
a
) and circumferential force (
b
) of a hollow elastic shell with an initial thickness
h
0 on external pressure at the values of the initial deflection:
1
-
A
=
1
■
10
-
2
,
2
-
A
=
1
■
10
-
3
,
3
-
A
=
1
■
10
-
4
,
4
-
A
=
1
■
10
-
5
~ w а
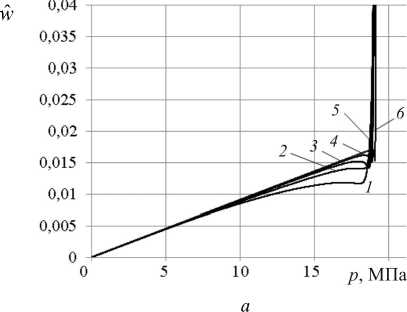
Рис. 3. Зависимости среднего прогиба (
а
) и окружного усилия (
б
) пустотелой упругопластической оболочки с начальной толщиной
h
0
от внешнего давления при значениях начальной погиби:
1
-
A =
1
■
10
-
2,
2
-
A =
7
■
10
-
3
,
3
-
A =
4
■
10
-
3
,
4
-
A
=
1 ■Ю
-
3
,
5
-
A
=
1
■
10
-
4
,
6
-
A
=
1
-
10
-
5
Fig. 3. Dependences of the average deflection (
a
) and the circumferential force (
b
) of a hollow elastic-plastic shell with an initial thickness
h
0 on external pressure at the values of the initial deflection:
1
-
A
=
1
■
10
-
2,
2
-
A
=
7
■
10
-
3,
3
-
A
=
4
■
10
-
3,
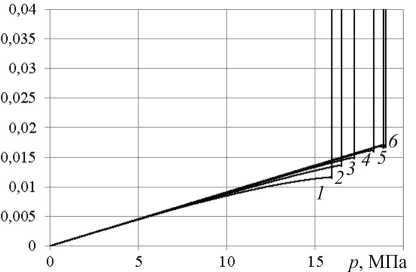
Рис. 4. Зависимости среднего прогиба (
а
) и окружного усилия (
б
) пустотелой упругопластической оболочки с начальной толщиной
h
0
/2 от внешнего давления при значениях начальной погиби:
1
-
A
=
2
■
10
-
2
,
2
-
A
=
2
■
10
-
3
,
3
-
A
=
2
■
10
-
4
,
4
-
A
=
2
■
10
-
5
,
5
-
A
=
2
■
10
-
6
,
6
- упругой оболочки
Fig. 4. Dependences of the average deflection (
a
) and the circumferential force (
b
) of a hollow elastic-plastic shell with an initial thickness
h
0/
2 on the external pressure at the values of the initial deflection:
1
-
A
=
2 ■Ю
-
2
,
2
-
A
=
2
■
10
-
3
,
3
-
A
=
2
■
10
-
4
,
4
-
A
=
2 ■Ю
-
5
,
5
-
A
=
2
■
10
-
6
,
6
is the elastic shell
Для вариантов расчета по модели сплошной среды с
L
= 120, 160 и 240 разброс критических давлений
p
* не превышает 1 %. Для дальнейших расчетов по упрощенной модели выбрана сетка с
L
= 120 элементам по окружности, для модели сплошной среды – сетка с
L
= 120 элементам вдоль половины окружности. Выбранные сетки являются достаточными для сходимости численного решения. Отличие критического давления
p
* на этих сетках для двух моделей составляет 4 %.
Аналогичные исследования сходимости численного решения для оболочки с относительной амплитудой начальной погиби
A
=
1
•
10
-
2 показали, что для упрощенной модели необходимо брать сетку с
L
= 240 элементам по окружности, а для модели сплошной среды – сетку с
L
= 160 элементам вдоль половины окружности. Для оболочки с толщиной
h
0 2 : для упрощенной модели необходимо брать сетку с
L
= 480 элементам по окружности, а для модели сплошной среды – сетку с
L
= 240 элементам вдоль половины окружности. Отличие критического давления
p
* на этих сетках для двух моделей составляет 3 %.
3.2. Численное исследование влияния пластических свойств материала оболочки на величину критической нагрузки
Исследовалась зависимость критической нагрузки от амплитуды начальной погиби для пустотелых упругой и упругопластической оболочек. Моделирование выполнялось в упрощенной постановке, основанной на гипотезах теории оболочек типа Тимошенко. Результаты расчетов приведены на рис. 2 (упругая постановка) и 3, 4 (упругопластическая постановка). Введены следующие обозначения:
h
N
N
s
= J°
ss
d
5,
N
=--
s-
0
°
Tr 0
.
Здесь
N
s
- окружное усилие,
G
T
- предел текучести,
о
T
=
280 МПа.
При обжатии пустотелой цилиндрической оболочки происходит неосесимметричная потеря устойчивости по второй форме в окружном направлении. До потери устойчивости как упругой, так и упругопластической оболочки наблюдается линейный рост окружного усилия Nˆ , а затем – его резкое падение. Падение интегральной силы связано с уменьшением продольной жесткости кольца в связи с его изгибом при выпучивании в упругих оболочках, а в упругопластических – этот эффект усиливается за счет упругой разгрузки в растянутых волокнах. В момент выпучивания пустотелых оболочек с начальными толщинами h0 и h0 2 величина относительного среднего прогиба v < 0,02 (рис. 2, 3, а) и v < 0,01 (рис. 4, а) соответственно, т.е. потеря устойчивости происходит при малых упругопластических деформациях. Установлено, что для упругой оболочки величина критической нагрузки p* слабо зависит от амплитуды начальной погиби A (рис . 2, б). При упругопластическом деформировании критическая нагрузка p* существенно зависит (до 20 %) от амплитуды начальной погиби А в исследованном диапазоне от 10-5 до 10-2 (см. рис. 3,4).
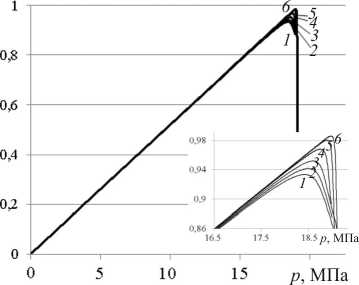
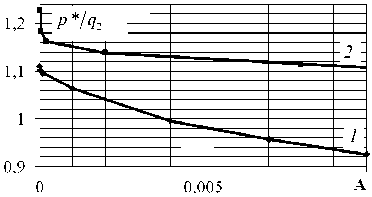
На рис. 5 приведены зависимости критической нагрузки
p
* от амплитуды начальной погиби
А
. Величина критической нагрузки
p
* отнесена к величине критической нагрузки
q
n
=
(
n
2
-
1
)
EJJR
3 для тонкого кругового кольца, нагруженного в своей плоскости внешней гидростатической нагрузкой при
n
=
2, здесь
EJ
– изгибная жесткость кольца в его плоскости [29]. С уменьшением толщины оболочки абсолютная величина критической нагрузки
p
* снижается, так как потеря устойчивости происходит при меньших степенях деформаций, при этом критические нагрузки упругопластических оболочек приближаются к критической нагрузке упругих оболочек.
Рис. 5. Зависимость критического (максимального) значения нагрузки от амплитуды начальной погиби пустотелых упругопластических оболочек:
1
– начальная толщина
h
0,
2
– начальная толщина
h
0 2
Fig. 5. Dependence of the critical (maximum) value of the load on the amplitude of the initial deflection of hollow elastic-plastic shells:
1
– initial thickness
h
0 ,
2
– initial thickness
h
0 2
3.3. Исследования области применимости модели основания Винклера для описания контактного взаимодействия упругопластических оболочек с заполнителем при внешнем давлении
Для оценки области применимости гипотезы Винклера при контактном взаимодействии упругопластической оболочки с упругой средой решалась задача о потере устойчивости цилиндрических оболочек с толстостенным упругим заполнителем при квазистатическом нагружении внешним давлением. Проводилось сравнение результатов численного моделирования, выполненного в рамках гипотез механики сплошной среды (1)–(5) и гипотез теории оболочек типа Тимошенко и основания Винклера (6)–(11) для оболочки с начальной толщиной
h
0 .
Параметрами модели толстостенного заполнителя как упругого тела являются модуль Юнга
E
, коэффициент Пуассона
V
, толщина
H
0. Они связаны с коэффициентом постели
k
соотношением [30]
k
=
Е
/ (
H
0
(
1
-
2
v
2
)
)
.
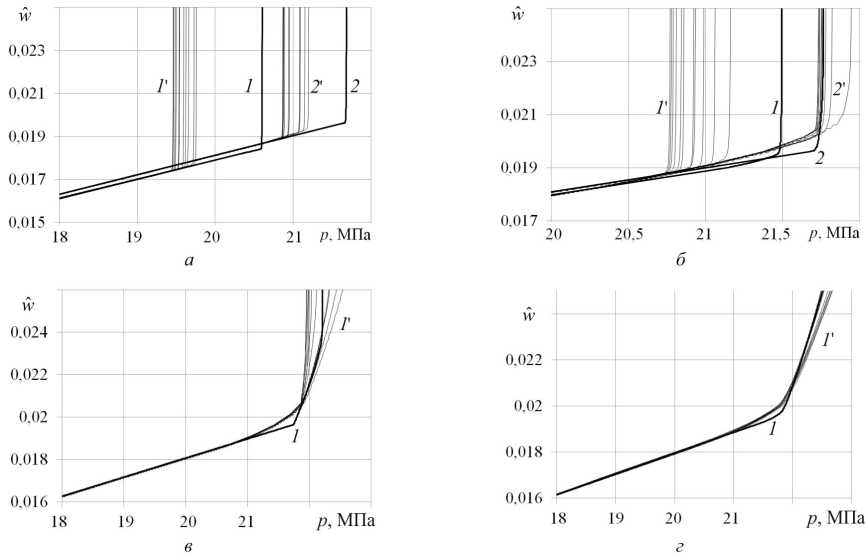
Рис. 6. Изменения относительного среднего прогиба
w
вблизи критической нагрузки:
к
=
3000 МПа/м (
a
),
к
=
5000 МПа/м (
б), к
=
7000 МПа/м (
в
),
к
=
10000 МПа/м (
г
):
1
-
A
=
1
■
10
-
2, оболочечная модель;
1
’ -
A
=
1
■
10
-
2, сплошная среда;
2
-
A
=
1
•
10
-
5, оболочечная модель;
2
’ -
A
=
1
■
10
-
5, сплошная среда
Fig. 6. Changes in the relative mean deflection near the critical load:
к
=
3000 MPa / m (
a
),
к
=
5000 MPa / m (
b
),
к
=
7000 MPa / m (
c
),
к
=
10000 MPa / m (
d): 1
-
A
=
1
^
10
-
2, shell model; 1' -
A
=
1
^
10
-
2, continuous medium;
2
-
A
=
1
^
10
-
5, shell model;
2
' -
A
=
1
^
10
-
5, continuous medium
Для каждого значения коэффициента постели
k
выполнена серия расчетов, в которых полагалось, что толщина заполнителя
H
0
=
(
1
*
13
)
h
0
, коэффициент Пуассона
v =
0,3, а модуль Юнга
E
определялся из соотношения (12). Параметры начальной погиби:
A
=
1
•
10
-
5 и
A
=
1
■
10
-
2,
n
= 2 и 3. Из двух расчетов с
n
= 2 и 3 выбирался вариант, в котором величина критической нагрузки
p
* была минимальной.
На рис. 6 приведены зависимости относительного среднего прогиба
w
ˆ в диапазоне внешнего давления
p
, близкого к критическому
p
* , при различных значениях коэффициента постели
k
. Толстыми линиями обозначены результаты расчетов по упрощенной модели, тонкими – серии расчетов по модели сплошной среды с различными толщинами заполнителя
H
0
=
(
1
*
13
)
h
0
.
В исследованном диапазоне толщины заполнителя
н
г
=
(
1
*
13
)
h
величина критического давления
p
* в каждой серии расчетов, выполненных в рамках модели сплошной среды, изменяется незначительно: разброс не превышает 1 %. Расхождение результатов по обеим методикам не превосходит 5 %.
Оболочки с большей амплитудой начальной погиби (A = 1 ■ 10-2) и с коэффициентом постели к = 3000 МПа/м и к = 5000 МПа/м теряли устойчивость по второй форме во всех вариантах расчетов. В расчетах по обеим методикам на начальной стадии закритического этапа деформирования поперечное сечение приобретает форму эллипса. Дальнейшее нагружение пустотелых оболочек приводит к смыканию внутренних диаметрально противоположных поверхностей оболочек (точки эллипса вблизи малой оси). У оболочек с заполнителем в местах выпучивания (точки эллипса вблизи большой оси) имеет место отрыв оболочки от заполнителя. Дальнейшее нагружение приводит к образованию двух диаметрально противоположных складок на месте выпу-чин. При к = 7000 МПа/м и к = 10 000 МПа/м во всех вариантах расчетов после момента потери устойчивости формируется одна складка. Потеря устойчивости оболочек с меньшей амплитудой начальной погиби (A = L10-5) происходила по второй или третьей форме либо с образованием одной локальной выпучины. В расчетах с коэффициентом постели к = 5000 МПа/м при отношении толщин H0/h = 3,8 потеря устойчивости оболочки происходила по третьей форме. В случае c H0/h = 9,13 потеря устойчивости реализовалась сначала по второй форме с образованием двух симметричных, диаметрально противоположных выпучин на плоскости симметрии, затем одна из выпу- чин прекращала расти, а вторая трансформировалась в складку. В местах выпучивания имеет место отрыв оболочки от заполнителя. В расчетах по оболочечной модели с основанием Винклера для данных коэффициента постели и относительной амплитуды начальной поги-би потеря устойчивости происходила по третьей форме.
3.4. Исследование влияния толщины и начальных несовершенств геометрии цилиндрической упругопластической оболочки с упругим заполнителем на формы потери устойчивости при внешнем давлении
Расчеты проводились в упрощенной постановке. Результаты исследований приведены на рис. 7, 8. Критическая нагрузка
p
* в диапазоне коэффициента постели
k
от 0 до 5000 МПа/м убывает с ростом амплитуды начальной погиби
А
(рис. 7). В расчетах величина контактного давления, действующего со стороны заполнителя на оболочку, существенно (на два порядка) ниже величины задаваемого внешнего давления. До момента потери устойчивости оболочки распределение контактного давления близко к однородному. В расчетах с амплитудой начальной погиби и величиной коэффициента постели менее 5000 МПа/м потеря устойчивости происходит по второй форме. В расчетах с амплитудой начальной погиби и величиной коэффициента постели до 500 МПа/м потеря устойчивости оболочки происходит по второй форме, от 500 до 5000 МПа/м – по третьей форме. Дальнейшее увеличение жесткости заполнителя приводит к локальной выпучине. На рис. 5 точками обозначены варианты расчета, в которых потеря устойчивости происходит по второй форме, квадратами – по третьей, и треугольниками – с образованием локальной выпучины. В процессе потери устойчивости происходит локальный отрыв оболочки от заполнителя в зонах выпучивания, и распределение контактного давления становится неоднородным.
На рис. 7, 8 приведены зависимости среднего прогиба от внешней нагрузки. С увеличением жесткости заполнителя (коэффициента постели
k
) увеличивается критическая нагрузка
p
* . В исследованном диапазоне изменения коэффициента постели 0
<
к
<
10000 МПа для оболочки с начальной толщиной
h
0 и амплитудой начальной погиби
A
=
140
-5
величина критической нагрузки
p
* возрастает на 12 %, с амплитудой начальной погиби
A =
1
•
10
-2
- на 28 %, а для оболочки с начальной толщиной
h
0 2 – увеличивается более чем в 4 раза, независимо от амплитуды начальной погиби. Величина среднего прогиба в момент потери устойчивости оболочки с начальной толщиной
h
0 изменяется от 0,12 до 0,2, с начальной толщиной
h
0 2 – изменяется от 0,1 до 0,4.
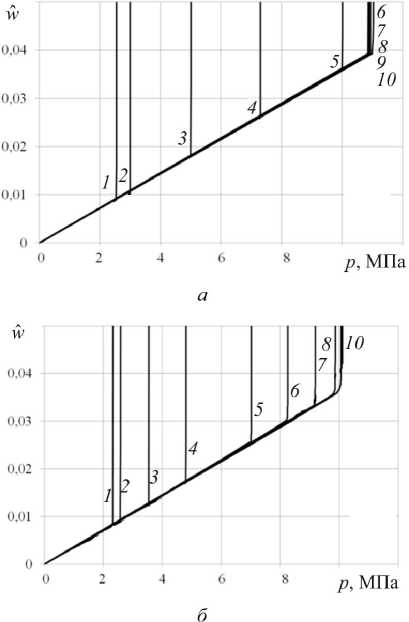
На рис. 9 приведены зависимости критического (максимального) значения нагрузки p* от коэффициента постели k. Точками обозначены варианты расчета, в которых потеря устойчивости происходит по второй форме, квадратами – по третьей, звездочками – по пятой, треугольниками – с образованием локальной выпучины. Рис. 7. Зависимость среднего прогиба оболочки с начальной толщиной h0 от нагрузки при величине амплитуды начальной погиби: A = 1 • 10-5 (а), A = 1 • 10-2 (б) и различных значениях коэффициента постели: 1 - к = 0, 2 - к = 100 МПа/м,
3
-
к
=
1000 МПа/м,
4 -к
=
2000 МПа/м,
5 -к
=
5000 МПа/м,
6
-
к
=
10 000 МПа/м
Fig. 7. Dependence of the average deflection of the shell with the initial thickness
h
0 on the load at the amplitude of the initial deflection:
A
=
1
•
10
-
5 (
a
),
A
=
1
•
10
-
2 (
b
) and different values of the bed coefficient:
1
-
к
=
0,
2
-
к
=
100 MPa/m,
3 -к
=
1000 MPa/m,
4
-
к
=
2000 MPa/m,
5
-
к
=
5000 MPa/m,
6
-
к
=
10 000 MPa/m
В расчетах величина контактного давления, действующего со стороны заполнителя на оболочку, существенно (на два порядка) ниже величины задаваемого внешнего давления. До момента потери устойчивости оболочки распределение контактного давления близко к однородному. В процессе потери устойчивости происходит локальный отрыв оболочки от заполнителя в зонах выпучивания, и распределение контактного давления становится неоднородным. При увеличении амплитуды начальной погиби величина критической нагрузки уменьшается. Влияние жесткости заполнителя на формообразование и критическую нагрузку с уменьшением толщины упругопластической оболочки проявляется сильнее. С увеличением коэффициента постели номер формы потери устойчивости изменяется со второй на третью – для более толстой оболочки, и со второй на третью и пятую – для более тонкой.
Рис. 8. Зависимость среднего прогиба оболочки с начальной толщиной
h
0 2 от нагрузки при величине амплитуды начальной погиби:
A
=
2
-
10
"
5 (
а
),
A
=
2 ■Ю
-
2 (
б
) и различных значениях коэффициента постели:
1
-
к
=
0;
2
-
к
=
100 МПа/м;
3
-
к
=
500;
4
-
к
=
1000 МПа/м;
5
-
к
=
2000 МПа/м;
6
-
к
=
3000 МПа/м;
7
-
к
=
4000 МПа/м;
8
-
к
=
5000 МПа/м;
9
-
к
=
7000 МПа/м;
10
-
к
=
10 000 МПа/м
Fig. 8. Dependence of the average deflection of the shell with the initial thickness
h
0 2 on the load at the amplitude of the initial deflection:
A =
2
-
10
"
5 (
a
),
A =
2 ■Ю
-
2 (
b
) and different values of the bed coefficient:
1
-
к
=
0,
2
-
к
=
100 MPa/m,
3
-
к
=
500,
4 - к
=
1000 MPa/m,
5
-
к
=
2000 MPa/m,
6 -к
=
3 000 MPa/m,
7 -к
=
4000 MPa/m,
8 -к
=
5000 MPa/m,
9 -к
=
7000 MPa/m,
10
-
к
=
10 000 MPa/m
Другими словами, утонение оболочки и увеличение жесткости заполнителя приводят к более высоким номерам форм потери устойчивости. Этот факт известен в теории устойчивости упругих стержней на упругом основании Винклера. При большой жесткости упругого заполнителя образуется локальная выпучина. С увеличением жесткости заполнителя повышается критическая нагрузка
p
* и средний прогиб в момент потери устойчивости. С уменьшением толщины оболочки увеличение жесткости заполнителя приводит к более
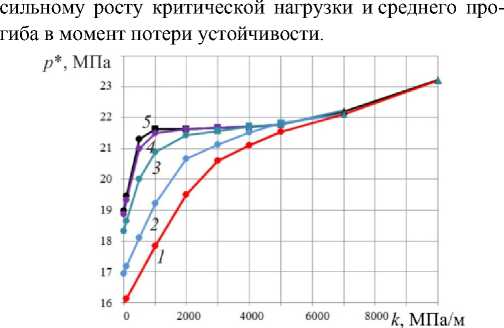
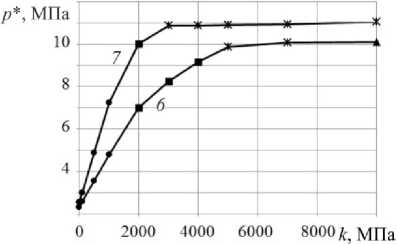
Рис. 9. Зависимости критического (максимального) значения нагрузки
p
* от коэффициента постели
Y
упругопластической оболочки с начальной толщиной
h
0 (
а
) и амплитудой начальной погиби:
1
-
A
=
Ь10
-
2
,
2
-
A
=
5
■Ю
-
3
,
3
-
A
=
k10
-
3
,
4
-
A
=
Ь10
-
4
,
5
-
A
=
1
■Ю-
5
; с начальной толщиной
h
0/
2 (
б
) и амплитудой начальной погиби:
6
-
A
=
2
■
10
-
2
,
7
-
A
=
2
■
10
-
5
Fig. 9. Dependences of the critical (maximum) value of the load p* on the bed coefficient
Y
of the elastoplastic shell with the initial thickness
h
0 (
a
) and the amplitude of the initial deflection:
1
-
A
=
1
^
10
-
2
,
2
-
A
=
5 ■Ю
-
3
,
3
-
A
=
1 ■Ю
-
3
,
4
-
A
=
1
-
10
"
4
,
5
-
A
=
1
■Ю-
5
; with initial thickness
h
0/
2 (
b
) and amplitude of initial deflection:
6
-
A
=
2
■
10
-
2
,
7
-
A
=
2
■
10
-
5
Заключение
При квазистатическом нагружении равномерным внешним давлением выпучивание упругопластических пустотелых и заполненных упругой средой оболочек
R
0
[h
=
14,5 ^29 происходит при малых упругопластических деформациях. При фиксированной жесткости основания Винклера изменение толщин заполнителя незначительно влияет на величину критического давления и хорошо согласуется с результатом, полученным в упрощенной оболочечной постановке с основанием Винклера в широком диапазоне жесткостей
k
= 0…10 000 МПа/м.
При этом формы потери устойчивости существенно изменяются в зависимости от толщины и жесткости заполнителя и амплитуды начальной погиби. Наличие заполнителя приводит к более высоким формам потери устойчивости, и даже к локальным. Результаты исследования показывают, что модель Винклера в сочетании с моделью теории оболочек имеет широкую область применимости в задачах контактного взаимодействия осесимметричных упругопластических оболочек с упругим заполнителем как при низких, так и при локальных формах потери устойчивости. Во всем рассмотренном практически значимом диапазоне геометрических и жестко-стных характеристик упругого основания погрешность применения модели Винклера не превышала 5 %. Преимуществом упрощенной постановки является существенное сокращение времени расчета по сравнению с полномасштабным моделированием. Следует отметить, что время расчета одного варианта при использовании компьютера с процессором 4.39 ГГц в упрощенной постановке составляет около 10 мин, а в пол- ной постановке – около 18 ч. Данный подход позволяет исследовать критические нагрузки и формы потери устойчивости оболочек, а также закритическое поведение оболочек с учетом начальных геометрических несовершенств, контактного взаимодействия и отрыва от основания.
Список литературы Исследование применимости модели основания Винклера для описания контактного взаимодействия упругопластических оболочек с заполнителем при внешнем давлении
- Исследование упругопластического деформирования цилиндрических оболочек при осевом ударном нагружении / А.И. Абакумов, Г.А. Квасков, С.А. Новиков, В.А. Синицин, A.А. Учаев // ПМТФ. - 1988. - № 3. - С. 150-153.
- Выпучивание упругопластических цилиндрических и конических оболочек при осевом ударном нагружении / B.Г. Баженов, М.С. Баранова, А.И. Кибец, В.К. Ломунов, Е.В. Павленкова // Ученые записки Казан. ун-та. Серия: Физ.-матем. науки. - 2010. - Т. 152, № 4. - С. 86-105.
- О влиянии заполнителя на критические параметры импульса давления при динамической потере устойчивости цилиндрической оболочки / В.В. Бендюков, В.В. Дерюшев, М.М. Лурье, П.Н. Овчаров // Научный вестник МГТУ ГА. -2005. - № 84 (2). - С. 131-137.
- Экспериментальное исследование упругопластического деформирования и потери устойчивости подкрепленных цилиндрических оболочек с заполнителем при изгибе / Е.Г. Гоник, А. И. Кибец, М.В. Петров, Т. Г. Федорова // Пробл. прочности и пластичности. - 2013. - Т. 75, № 3. - С. 215-220.
- Иванов В.А. Определение реакции заполнителя в задачах взаимодействия его с оболочкой // Вестник Казанского технологического университета. - 2011. - № 8. - C. 224-228.
- Ильгамов М.А., Иванов В.А., Гулин Б.В. Прочность, устойчивость и динамика оболочек с упругим заполнителем. -М.: Наука, 1977. - 331 с.
- Луговой П.З., Прокопенко Н.Я. Влияние упругого основания на дисперсию гармонических волн в продольно подкрепленных цилиндрических оболочках // Прикладная механика. - 2015. - Т. 51, № 5. - С. 116-124.
- Прикладные задачи механики композитных цилиндрических оболочек / Ю.С. Соломонов, В.П. Георгиевский, А.Я. Нед-бай, В.А. Андрюшин. - М.: Изд-во Физматлит, 2013. - 343 с.
- Тарлаковский Д.В., Федотенков Г.В. Воздействие нестационарного давления на цилиндрическую оболочку с упругим заполнителем // Ученые записки Казан. ун-та. Серия: Физ.-матем. науки. - 2016. - Т. 158, № 1. - С. 141-151.
- Stability improvement of thin isotropic cylindrical shells with partially filled soft elastic core subjected to external pressure / A.P. Dash, R. Velmurugan, M.S.R. Prasad, R.S. Sikarwar // Thin-Walled Structures, B. - 2016. - Vol. 98. - P. 301-311 DOI: 10.1016/j.tws.2015.09.028.
- Eksi S., Kaptiand A.O., Genel K. Effects of Pre-Forming Process and PVC Foam Reinforcement on the Deformation Behavior of Aluminum Tube under Axial Loading // Acta Physica Polonica A. - 2017. - No. 3-II, Vol. 132. - P. 875-878.
- Nonlinear dynamic stability of the orthotopic functionally graded cylindrical shell surrounded by Winkler-Pasternak elastic foundation subjected to a linearly increasing load / Kang Gao, Wei Gao, Di Wu, Chongmin Song // Journal of Sound and Vibration. -2018. - No. 415. - P. 147-168. DOI: 10.1016/j.jsv.2017.11.038
- Karam G.N., Gibson L.J. Elastic buckling of cylindrical shells with elastic cores - II // Experiments International Journal of Solids and Structures. - 1995. - Vol. 32 (8-9). - P. 1285-1306. DOI: 10.1016/0020-7683(94)00148-P.
- Karam G.N., Gibson L.J. Elastic buckling of cylindrical shells with elastic cores. I // Analysis Int J Solids Structures. -1995. - Vol. 32. - P. 1259-1263.
- Nobili A., Radi E., Lanzoni N. A cracked infinite Kirchhoff plate supported by a two-parameter elastic foundation // J. Eur. Ceram. Soc. - 2014. DOI: 10.1016/j.jeurceramsoc.2013.12.029
- Buckling, postbuckling and imperfection-sensitivity: Old questions and some new answers / H. Obrecht, B. Rosenthal, P.Fuchs, S. Lange, C. Marusczyk // Comput. Mech. - 2006. -Vol. 37. - P. 498-506. DOI: 10.1007/s00466-005-0732-z
- Buckling patterns of complete spherical shells filled with an elastic medium under external pressure / M.Sato, M.A. Wadee, K. Iiboshi, T. Sekizawa, H. Shima // International Journal of Mechanical Sciences. - 2012. DOI: 10.1016/j.ijmecsci.2012.02.001
- Power Law of Critical Buckling in Structural Members Supported by a Winkler Foundation / M. Sato, S. Harasawa, Y. Konishi, T. Maruyama, S.J. Park // Journal of Mechanics. -2017. - Vol. 33, no 3. - P. 369-374. DOI: 10.1017/jmech.2016.112
- Shaterzadeh A.R., Foroutan K. Non-Linear Analysis of Asymmetrical Eccentrically Stiffened FGM Cylindrical Shells with Non-Linear Elastic Foundation // Journal of Solid Mechanics. -2017. - Vol. 9, no. 4. - P. 849-864.
- Ye L., Lu G., Ong L.S. Buckling of a thin-walled cylindrical shell with foam core under axial compression // Thin-Walled Structures. - Vol. 49, no 1. - P. 106-111. DOI: 10.1016/j.tws.2010.08.011.
- Верификация конечно-элементного решения трехмерных нестационарных задач упругопластического деформирования, устойчивости и закритического поведения оболочек / А.А. Артемьева, В.Г. Баженов, А.И. Кибец, П.В. Лаптев, Д.В. Шошин // Вычислительная механика сплошных сред. - 2010. - Т. 3, № 2. - С. 5-14.
- Васин Р.А., Ильюшин А.А., Моссаковский П.А. Исследование определяющих соотношений и критериев разрушения на сплошных и толстостенных трубчатых цилиндрических образцах // Изв. РАН. МТТ. - 1994. - № 2. -С. 177-184.
- Коробейников С.Н. Численное решение уравнений с особенностями деформирования упругопластических оболочек вращения // Вычислительные технологии. - 2001. - Т. 6, № 5. - С. 39-59.
- Применение твердотельных конечных элементов в задачах расчета оболочек / С.А. Капустин, Ю.А. Чурилов, В.А. Горохов, А.А. Рябов, В.И. Романов, Д.А. Плакунов // Пробл. прочности и пластичности. - 2017. - № 2. - С. 204-219.
- Зефиров С.В. Импульсное деформирование и контактное взаимодействие упругопластических элементов осесиммет-ричных конструкций // Прикладные проблемы прочности и пластичности. Алгоритмизация решения задач упругости и пластичности: Всесоюз. межвуз. сб. / Горьк. ун-т. - 1984. - С. 152-153.
- Баженов В.Г., Зефиров С.В., Цветкова И.Н. Численное моделирование задач нестационарного контактного взаимодействия деформируемых конструкций // Прикладные проблемы прочности и пластичности. Численное моделирование физико-механических процессов: межвуз. сб. - М.: Товарищество научных изданий КМК, 1995. - Вып. 52. - С. 154-160.
- Пакет программ «Динамика-2» для решения плоских и осесимметричных нелинейных задач нестационарного взаимодействия конструкций со сжимаемыми средами / В.Г. Баженов, С.В. Зефиров, А.В. Кочетков, С.В. Крылов, В.Р. Фельдгун // Математическое моделирование. - 2000. - Т. 12 (6). - С. 67-72.
- Баженов В.Г., Ломунов В.К. Исследование упругопла-стического выпучивания оболочек вращения при ударном нагру-жении // Прикладные проблемы прочности и пластичности: все-союз. межвуз. сб. / Горьк. ун-т. - 1975. - Вып. 2. - С. 44-50.
- Алфутов Н.А. Основы расчета на устойчивость упругих систем. - М.: Машиностроение, 1978. - 312 с.
- Пастернак П. Л. Основы нового метода расчета фундаментов на упругом основании при помощи двух коэффициентов постели. - М.: Гос. изд-во литературы по строительству и архитектуре, 1954. - 56 с.


